| 栤戣侾
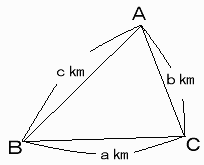
丂嶰妏宍偺捀揰俙丆俛丆俠偺埵抲偵俁峑偑偁傝丄偙偺俁峑傪楢寢偡傞僱僢僩儚乕僋乮偳偺俀峑傕僱僢僩儚乕僋傪捠偟偰丄峴偒棃偱偒傞傛偆偵偡傞乯傪寢傇寁夋偑偁傝傑偡丅 偨偩偟丄俛俠亖倎倠倣丆俠俙亖倐倠倣丆俙俛亖們倠倣丂偱偡丅 |

偝偰丄偄偒側傝嶰妏宍偺偲偒偼丄戝曄偩偐傜丄惓曽宍偱傒傫側峫偊偰偔偩偝偄丅
仏婛偵丄惗搆偵攝晍偟偰抲偄偨侾曈偑侾侽們倣惓曽宍偺岤巻偱丄偄傠偄傠側愝寁恾傪彂偒巒傔傞丅乯
彂偄偨傜丄掕婯偱挿偝傪應偭偰偔偩偝偄丅僌儖乕僾偱弌偟崌偭偰偔偩偝偄丅
栜榑丄侾曈傪倎倠倣偺偲偒偼丄併乮儖乕僩乯偑昁梫偵側傞偐傜偹丅
|
栤戣俀
丂惓曽宍偺捀揰俙丆俛丆俠丆俢偺埵抲偵係峑偑偁傝丄偙偺係峑傪楢寢偡傞僱僢僩儚乕僋乮偳偺俀峑傕僱僢僩儚乕僋傪捠偟偰丄峴偒棃偱偒傞傛偆偵偡傞乯傪寢傇寁夋偑偁傝傑偡丅 |
偙偙偵丄庼嬈拞偵惗搆偑峫偊偨愝寁恾偑偁傝傑偡丅
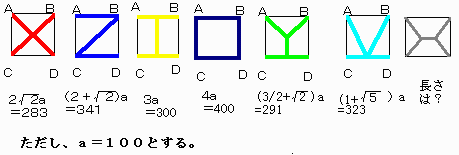
愝寁恾偺拞偱丄堦斣抁偄偺偼懳妏慄偺亊報偺僱僢僩偱偡偹丅
偟偐偟丄堦斣塃偼恾偩偗偱丄挿偝偼弌偰偄傑偣傫偹丅
愭惗丄掕婯偱應偭偰傒偨傜丄偳偆偱偡偐丅
偦偆偩偹丄偱偼應偭偰偔偩偝偄丅
懳妏慄偼侾曈偑侾侽們倣偱偡偐傜丄偩偄偨偄丄
俀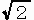 亊侾侽亖俀俉丏俁僙儞僠偱偡丅
亊侾侽亖俀俉丏俁僙儞僠偱偡丅
傛偔丄偦偙傑偱丄應傟偨偹丅師偓偵丄堦斣塃椬傝偼偳偆偱偡偐丠
丂愭惗両偳偆傕俀俉丏俁僙儞僠傛傝抁偄傒偨偄偱偡丅
偦偆偱偡偹丅偱偼丄搑拞偺岎揰偼偳偙偵庢傞偲傛偄偱偡偐丠
偄傠偄傠側丄敪憐偑偱偰偒傑偟偨偑丄側偤丠偲栤傢傟傞偲摎偊傜傟傑偣傫丅
丂愭惗両僊僽傾僢僾偱偡丅嫵偊偰偔偩偝偄丅偙偙傑偱丄峫偊偨偐傜丅
偦傟偱偼丄傒傫側偲堦弿偵峫偊偰傒傑偟傚偆丅
幚偼丄嶰妏宍偺応崌傪抦偭偰抲偔昁梫偑偁傝傑偡偺偱丄弴偵偄偒傛丅
丂傑偢丄師偺掕棟傪徹柧偟傑偡丅
| 掕棟侾 惓嶰妏宍偺撪晹偺揰偐傜俁曈傑偱偺嫍棧偺榓偼堦掕偱偁傞丅 |
亙徹柧亜
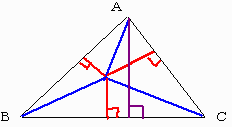 惓嶰妏宍偺侾曈偺挿偝傪倎偲偟偰丄嶰妏宍偺柺愊傪峫偊傞丅
惓嶰妏宍偺侾曈偺挿偝傪倎偲偟偰丄嶰妏宍偺柺愊傪峫偊傞丅
仮俹俛俠亄仮俹俠俙亄仮俹俙俛亖仮俙俛俠
丂(侾/俀)倎倶亄(侾/俀)倎倷亄(侾/俀)倎倸亖(侾/俀)倎倛
亪倶亄倷亄倸亖倛
丂丂乮偨偩偟丄倛偼仮俙俛俠偺崅偝偲偡傞乯
偝偰丄偙偺墳梡傪梡偄偰嵟抁僔儍僞僀僫乕栤戣偑夝偗傑偡丅
|
栤戣侾丂俁妏宍偺奺捀揰偐傜嫍棧偺榓偑嵟彫偵側傞揰傪尒偮偗傛丅 乮偙傟偼僼儔儞僗偺戝悢妛幰僼僃儖儅乕偑僀僞儕乕偺暔棟妛幰僩儕僠僃儕偵弌戣乯 |
亙徹柧亜俀偮偺俁妏宍偵暘偗偰丄寢榑偑暘偐偭偰偄側偄偺偱丄偙偺揰偑嵟彫側傞偙偲傪徹柧偟傑偡丅
嘆俁妏宍偺妏偑偡傋偰侾俀侽並埲壓偺応崌丂
嘇 俁妏宍偺侾妏偑侾俀侽並傛傝戝偒偄応崌
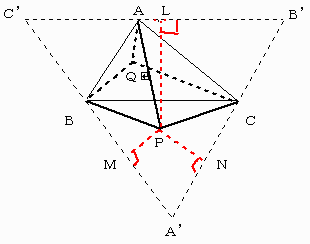 嘆偺応崌丂
嘆偺応崌丂
梌偊傜傟偨俁妏宍傪俙俛俠偲偟丄擟堄偺揰傪俹偲偡傞丅
俙俹丆俛俹丆俠俹偺岎妏偑偡傋偰侾俀侽並偵側傞偲偒嵟彫側揰俻偲側傞偙偲傪尵偆丅
俙丆俛丆俠傪捠偭偰丆俙俻丆俛俻丆俠俻偵悅捈側捈慄傪堷偄偰俁妏宍俙乫俛乫俠乫傪嶌傞丅
偙偺俁妏宍偼丄佢俙俻俛亖佢俛俻俠亖佢俠俻俙亖侾俀侽並丂傛傝惓嶰妏宍偱偁傞丅
擟堄偺揰俹偐傜俁曈俛乫俠乫丆俠乫俙乫丆俙乫俛乫偵壓偟偨悅慄偺懌傪俴丄俵丄俶偲偡傞偲丄
俹俙亄俹俛亄俹俠亞俹俴亄俹俵亄俹俶亖俻俙亄俻俛亄俻俠
乮俁妏宍偺曈偺挿偝偺晄摍幃偲掕棟侾偐傜乯
嘇偺応崌偼峫椂拞偱偡丅丂丂亙堦墳徹柧廔傢傝亜
師偺奜愙墌傪壛偊傑偡丅
|
掕棟俀
丂惓俁妏宍俙俛俠偺暯柺忋偺擟堄偺揰傪俹偲偟偰丄師偺晄摍幃偑惉傝棫偮丅 |
亙徹柧亜乮仏僩儗儈乕偺掕棟偺堦斒壔偟偨傕偺傪棙梡偟傑偡乯
擟堄偺係揰俙丆俛丆俠丆俹偵偮偄偰乮係妏宍偼偹偠傟偨応崌傕椙偄乯丄
巐曈宍俙俛俠俢偵偮偄偰丄堦斒偺僩儗儈乕偺掕棟偼
俙俠丒俛俹亄俙俛丒俠俹亞俛俠丒俙俹
乮偙偺徹柧偼傗傜偹偽丄偙傟偼暋慺悢傪梡偄偰屻偱偟傑偡丅乯
惓俁妏宍傛傝丄俙俠亖俙俛亖俛俠丂偩偐傜
丂俛俹亄俠俹亞俙俹
懠偺俀偮偺応崌傕摨條偱偡丅丂丂亙徹柧廔亜
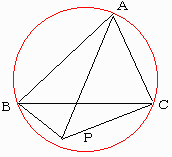 拲丗揰俹偑仮俙俛俠偺奜愙墌忋偵側偄偲偒
拲丗揰俹偑仮俙俛俠偺奜愙墌忋偵側偄偲偒
拲堄丗偙偺晄摍幃偺娭學偼墌偵奜愙偡傞係妏宍偺僩儗儈乕偺掕棟偐傜丄摍崋偑惉傝棫偮偺偼揰俹偑仮俙俛俠偺奜愙墌忋偵偁傞偲偒偵尷傞丅
椺偊偽丄揰俹偑屖俛俠忋偵偁傞偲偒丄
丂摍幃丂俛俹亄俠俹亖俙俹丂偑惉傝棫偪丄懠偺俀偮偼晄摍幃偱偁傞丅
偙傟偼丄揰俹偑嶰妏宍俙俛俠偺奜愙墌忋偵偁傞偲偒偵惉傝棫偮偙偲傪偟傔偟偰偄傑偡丅
|
掕棟俁丂巐曈宍俙俛俠俢偵偮偄偰丄堦斒偺僩儗儈乕偺掕棟偼 丂丂俙俛丒俠俢亄俙俢丒俛俠亞俙俠丒俛俢 |
亙徹柧亜 暋慺悢暯柺忋偱係揰俙丄俛丄俠丄俢偺嵗昗傪偦傟偧傟兛丄兝丄兞丄兟 偲偡傞丅
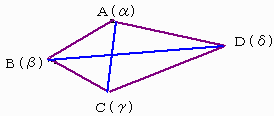
偙偙偱丄倅亖(兛亅兝)(兞亅兟)丆 倂亖(兞亅兝)(兛亅兟)偲偍偔偲丄
倅亅倂亖(兛亅兝)(兞亅兟)亅(兞亅兝)(兛亅兟)
丂丂亖(兛亅兞)(兝亅兟)偲側傝丄
乥倅乥亄乥倂乥亞乥倅亅倂乥 亙椺偺嶰妏晄摍幃亜
拲丗堦斒偵丄暋慺悢倃丄倄偵偮偄偰丄
丂丂丂乥倃乥乥倄乥亖乥倃倄乥偼惉棫
偨偩偟丄摍崋偼丄係揰俙丄俛丄俠丄俢丂偑摨堦墌廃忋偵偁傞偲偒惉傝棫偮丅
偝偁乕丄傕偆堦懅偩偐傜丄傒傫側婃挘傠偆偹丅
嵟屻偺掕棟偱乕偡丅
|
掕棟係丂 仮俙俛俠偺曈俛俠丆俠俙丆俙俛傪侾曈偲偟偰惓俁妏宍俠俛俢丆俙俠俤丆俛俙俥傪仮俙俛俠偺奜懁偵嶌傞偲丄師偺偙偲偑惉傝棫偮丅
乮侾乯俢俙亖俤俛亖俥俠 |
亙徹柧亜 偙偺徹柧偼 暋慺暯柺忋偱帵偟傑偡丅
俁揰俙丄俛丄俠偺嵗昗傪偦傟偧傟兛丄俷丄兞 偲偡傞丅
乮偨偩偟丆俷偼尨揰偲偡傞丅乯
乮仏夞揮偵埿椡傪敪婗偡傞偺偑暋慺悢偱偡丅乯
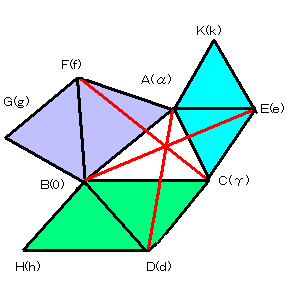
偝傜偵丄俁揰俢丄俤丆俥偺嵗昗傪偦傟偧傟倓丆倕丆倖偲偟傑偡丅
揰俥偺嵗昗偼 慄暘俛俙傪尨揰偺廃傝偵侾俀侽並夞揮偝偣偨揰傪俧偲偟丄儀僋僩儖
亪 倖亖冎兛亄兛亖(冎亄侾)兛亖亅兛冎2
揰俢偺嵗昗偼 慄暘俛俠傪尨揰偺廃傝偵俀係侽並夞揮偝偣偨揰傪俫偲偟丄儀僋僩儖 俫(兞冎2)丆俢(兞冎2亄兞)
亪
揰俤偺嵗昗偼丆慄暘俙俠傪揰俙偺廃傝偵侾俀侽並夞揮偝偣偨揰傪俲偲偟丄儀僋僩儖
俲乷冎(兞亅兛 )亄兛 乸丆俤乷冎(兞亅兛 )亄兛亄(兞亅兛 )乸
亪
偙傟偐傜丄
摨條偵偟偰丄
埲忋偐傜丄
嵟屻偵丄媮傔傞嵟抁宱楬偺挿偝偼
嘇 俁妏宍偺侾妏偑侾俀侽並傛傝戝偒偄応崌
佢俙亜侾俀侽並 偺偲偒丄俙俛亄俙俠丂偑丂嵟彫偵側傝丄揰俹偼揰俙 偦偺傕偺偱偡丅
愭惗丄傕偆旀傟偨乕丅
嘆俁妏宍偺妏偑偡傋偰侾俀侽並埲壓偺応崌
丂偝傜偵丄偙偺惓嶰妏宍偺奜愙墌偲偺岎揰傪傒偮偗偰偔偩偝偄丅
嘇 俁妏宍偺侾妏偑侾俀侽並傛傝戝偒偄応崌
偝偰丄尦偵丄傕偳傝傑偡丅惓曽宍偱偡偑丄
傕偆丄暘偐偭偨偹丅
拲丗倎亖侾侽侽偺偲偒丄嵟抁嫍棧偼俀俈俁丂偵側傞傛丅
亙嶲峫丂暥專亜丂悢妛傂偲傝椃丂愇扟丂栁丂尰戙悢妛幮
俧(冎兛)丄俥(冎兛亄兛)
倓亖兞冎2亄兞
亖(冎2亄侾)兞
亖亅冎兞
倕亖冎(兞亅兛 )亄兞
丂亖(冎亄侾)兞亅冎兛
丂亖亅兞冎2亅冎兛
亖倧亅倕
亖兞冎2亄冎兛
亖冎(兛亄冎兞)
亖冎
堦搙偵徹柧偱偒傑偡丅亙仏暋慺悢偺埿椡偱偡丅亜
丂乥俢俙乥亖乥兛亄冎兞乥 丒丒丒乮摎乯
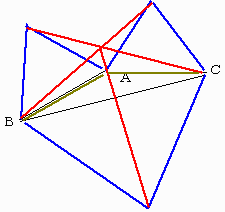
偠傖乕丄傑偲傔傞傛丅
丂媮傔傞愝寁恾偼岎妏偑偡傋偰侾俀侽並偲側傞揰傪扵偟傑偡丅
偦偺揰偼侾偮偺曈傪惓嶰妏宍偺侾曈偲偟偰丄斀懳懁偵嶌傝丄傕偆侾偮偺懠偺揰偲寢傃傑偡丅
偙傟偑傕偲傔傞拞宲揰偱偡丅
嵟抁嫍棧偼俢俙亖俤俛亖俥俠偱偡丅
佢俙亜侾俀侽並 偺偲偒丄俙俛亄俙俠丂偑丂嵟彫偵偵側傝丄揰俹偼揰俙偦偺傕偺偱偡丅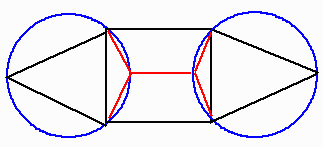
乵係(侾/俀亐們倧倱俁侽亱)亄乷侾亅俀(侾/俀亊倲倎値俁0亱)乸乶倎
亖(侾亄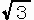 )丂丒丒丒乮摎偊乯
)丂丒丒丒乮摎偊乯
偙傟傪傕偲偵丄惓俆妏宍丄惓俇妏宍傕峫偊偰偔偩偝偄丅
傛乕偟丄偙傟偱丄杮擔偺亙悈偺棳傟亜偺庼嬈傪廔傢傝傑偡丅
丂丂丂丂丂丂丂婒晫導棫奀捗杒崅摍妛峑丂悢妛壢嫵桜丂悈栰丂棽惗
丂丂丂丂丂丂丂帺戭丗mizuryu@aqua.ocn.ne.jp