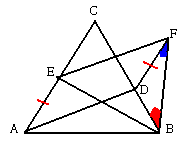
| 栤丂戣侾 俁妏宍俙俛俠偵偍偄偰丆佢俙丆佢俛偺俀摍暘慄偑懳曈偲岎傢傞揰傪丆偦傟偧傟丄俢丆俤偲偟丄 俀摍暘慄偳偆偟偺岎揰傪俹偲偡傞丅 乮侾乯佢俙亖佢俛偺偲偒丄俹俢亖俹俤偲側傞偙偲傪徹柧偣傛丅 乮俀乯媡偼惓偟偄偐丠偮傑傝丄俹俢亖俹俤偲偡傞偲佢俙亖佢俛偲側傞偐丅 |
僐儊儞僩 媡偑忢偵惓偟偄偲偼尷傜側偄椺偱偡丅抦偭偰偄側偄偲婥偑偮偒偵偔偄丅 |
徹柧 佢俙亖俀兛丄佢俛亖俀兝偲偡傞丅 
乮侾乯佢俙亖佢俛 偲偡傞偲丄兛亖兝偩偐傜丄仮俙俛俹偼俀摍曈嶰妏宍偲側傝丄俙俹亖俛俹 傑偨丄兛亖兝偩偐傜丄仮俙俛俢佭俛俙俤偲側傝丄俙俢亖俛俤傕偱傞丅 傛偭偰丄俹俢亖俙俢亅俙俹亖俛俤亅俛俹亖俹俤 亪 俹俢亖俹俤 徹柧廔 乮俀乯 俹俢亖俹俤 偐偮俀摍曈嶰妏宍偱側偄傛偆側仮俙俛俠偑偁傞偙偲傪妋偐傔傛偆丅 偮傑傝丄媡偑惉棫偟側偄偙偲傪帵偟偦偆丅 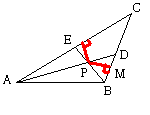
俹偐傜俛俠丄俙俠偵壓偟偨悅慄偺懌傪丄偦傟偧傟丄俵丄俶偲偡傞丅 俹偼仮俙俛俠偺妏偺俀摍暘慄偺岎揰乮撪怱乯偩偐傜丄俹俵亖俹俶丅 偙傟偲丄壖掕偺俹俢亖俹俤偐傜丄俀偮偺捈妏嶰妏宍俹俵俢偲俹俶俤偼崌摨偲側傝丄 佢俹俢俵亖佢俹俤俶 丒丒丒嘆 偑摼傜傟傞丅 偙偙偱丄俵偲俶偺埵抲娭學偵偮偄偰丄師偺応崌偑峫偊傜傟傞丅 応崌嘥丗俵丄俶偲傕巐妏宍俠俤俹俢偺曈忋偵側偄偲偒丅 応崌嘦丗俵丄俶偲傕巐妏宍俠俤俹俢偺曈忋偵偁傞偲偒丅 応崌嘨丗俵丄俶偺堦曽偺傒偑巐妏宍俠俤俹俢偺曈忋偵偁傞偲偒丅 応崌嘥偺偲偒丄佢俹俢俵亖180並亅乮兛亄俀兝乯偐偮佢俹俤俶亖180並亅乮俀兛亄兝乯丅 偙偙偱丄嘆 傛傝丄兛亖兝丄偮傑傝丄佢俙亖佢俛 偲側傞丅 応崌嘦偺偲偒丄 佢俹俢俵亖兛亄俀兝 偐偮 佢俹俤俶亖俀兛亄兝 偙偙偱丄嘆 傛傝丄兛亖兝丄偮傑傝丄佢俙亖佢俛 偲側傞丅 応崌嘨偺偲偒丄俵偑巐妏宍俠俤俹俢偺曈忋偵側偔丄俶偑巐妏宍俠俤俹俢偺曈忋偵偁傞偲偡傞 佢俹俢俵亖180並亅乮兛亄俀兝乯偐偮 佢俹俤俶亖俀兛亄兝 偙偙偱丄嘆 傛傝丄兛亄兝亖60並 偟偨偑偭偰丄佢俙俠俛亖180並亅乮俀兛亄俀兝乯亖60並 傑偨丄佢俙俠俛亖60並偱偁傟偽丄仮俹俵俢佭仮俹俶俤 偲側傝丄 俹俢亖俹俤偲側偭偰偄傞偙偲傕傢偐傞丅偮傑傝丄佢俙亖佢俛偲偼尷傜側偄椺偑柍悢偵偁傞丅 師偵丄応崌嘨偱丄俵偑巐妏宍俠俤俹俢偺曈忋偵偁傝丄俶偑巐妏宍俠俤俹俢偺曈忋偵側偄偲 偡傞偲偒傕傑偭偨偔偺摨條偱偁傞丅 埲忋偵傛偭偰丄俹俢亖俹俤偲偡傞偲丄 佢俙亖佢俛偲側傞偐丄偁傞偄偼丄佢俠亖60並偲側傞応崌偑偁傞丅 徹柧廔 |