平成14年8月10日
 [流れ星]
[流れ星]
第102回数学的な応募問題解答
<解答募集期間:7月21日~8月10日>
[定積分]
太郎さんは、この夏補習で「数学Ⅲの入試問題」を解説する予定です。次の2問を考えてください。
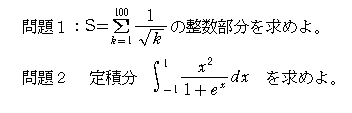
No1「H7K」さん 7/21:14時51分受信 更新8/10
問題1
以後,int^a_b 1/sqrt{k}dk=s(a,b)とおく.
1/sqrt(x)は単調減少なので,
s(0,100)>1+s(1,100)>S>s(1,101) (s(0,1)=2なので)
s(1,100)=20-2=18,s(1,101)=2sqrt{101}-2,10.5>sqrt{101}>10より
19=1+s(1,100)>S>s(1,101)>18
よって,S=18.//
問題2
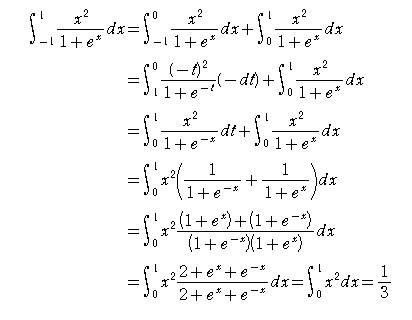
NO2「kashiwagi」さん 7/21:21時57分受信 更新8/10
第102解答
問1.
求めるものは(1/√1)+(1/√2)+(1/√3)+―――――――――――+(1/√100)の整数部分であるが、この値はY=1/√Xという関数のX=1~100までの区間を1の幅で区切った区分求積に他ならない。即ち、Y=1/√X、X=1、X=100及びY=0で囲まれる面積である。因って積分すると、
∫1001(1/√X)dX=18となる。これより求める整数の値は18である。
問2.
まず1+ex=Xと置換するとx=log(X-1)、dx=dX/(X-1)、X=(e+1)/e~e+1であるから、求めるものをIと置くと
I=∫e+1(e+1)/e(log(X-1))2/X(X-1)dX
部分分数に直し計算すると、
=2/3-∫e+1(e+1)/e(log(X-1))2/XdX
ここで再度置換する、t=log(X-1)、etdt=dx、t=-1~1
=2/3-I-∫1-1 (et-1)/(et+1)dt
ところで 関数(et-1)/(et+1)は奇関数であるから-1~1まで積分するとゼロとなる。因って求める値は2I=2/3より、I=1/3である。
NO3「中川」さん
7/22:01時11分受信 更新8/10

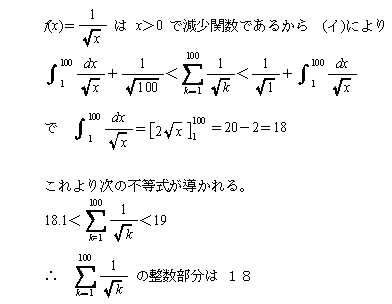
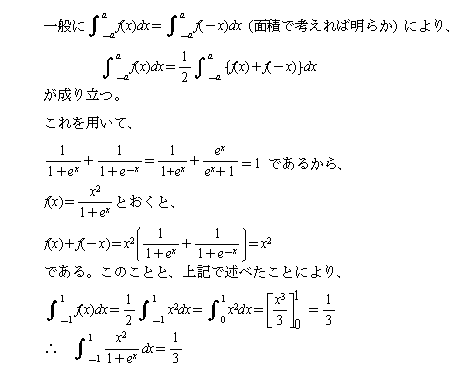
NO4「BossF」さん 7/24:18時30分受信 更新8/10
お久しぶりです.
こちらは夏本番ですが、いかがお過ごしですか?
[解]
区間[a,b]における定積分を∫(a,b)f(x)dx とし
F(b)-F(a)を、[F(x)](a,b) と表すことにします。
(1)
T=∫(0,100)1/√(x+1)dx (=∫(1,101)1/√xdx)
U=1+∫(1,100)1/√xdx
とおくと、グラフより明らかに T<S<U です。
ところが
T=[2√x](1,101)=20.…-2=18.…
U=1+[2√x](0,100)=1+20-2=19
ですから、Sの整数部分は 18 ■
(2)
まず、一般に 1/(1+x)+1/{1+(1/x)}=1 …①であることに注意します。
与式=∫(-1,0) x2/(1+ex )dx+∫(0,1)
x2/(1+ex )dx
=∫(1,0) (-t)2/(1+e(-t) )d(-t)+∫(0,1) x2/(1+ex
)dx
=∫(0,1) {x2/(1+e-x )+ x2/(1+ex )}dx
=∫(0,1) x2dx (∵①)
=1/3 …答
No5「スモークマン」さん 7/28:10時29分受信 更新8/10
求める値をSとすると、図形的には、
S-1<∫2√xdx=18:(1~100までの積分)
18<∫2√xdx:(1~101までの積分)<S
以上より、18<S<19 から、18であるとわかった!
![]()
