丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂暯惉侾係擭侾侽寧俀侽擔
 [棳傟惎]
[棳傟惎]
丂丂丂丂丂丂丂丂戞10俇夞悢妛揑側墳曞栤戣夝摎
丂丂丂丂丂丂丂丂丂丂亙夝摎曞廤婜娫丗侾侽寧侾擔乣侾侽寧俀侽擔亜
乵儀僉忔偺榓乶
丂丂丂
仏丂懢榊偝傫偼丄夁嫀偺擖帋栤戣傪挱傔偰偄偨偲偙傠丄婒晫戝妛偵偱偰偄偨師偺栤戣傪敪尒偟傑偟偨丅奆偝傫丄僠儍儗儞僕偔偩偝偄丅

俶俷侾乽拞愳乿偝傫丂丂9/30:丂03帪45暘丂庴怣丂峏怴10/20
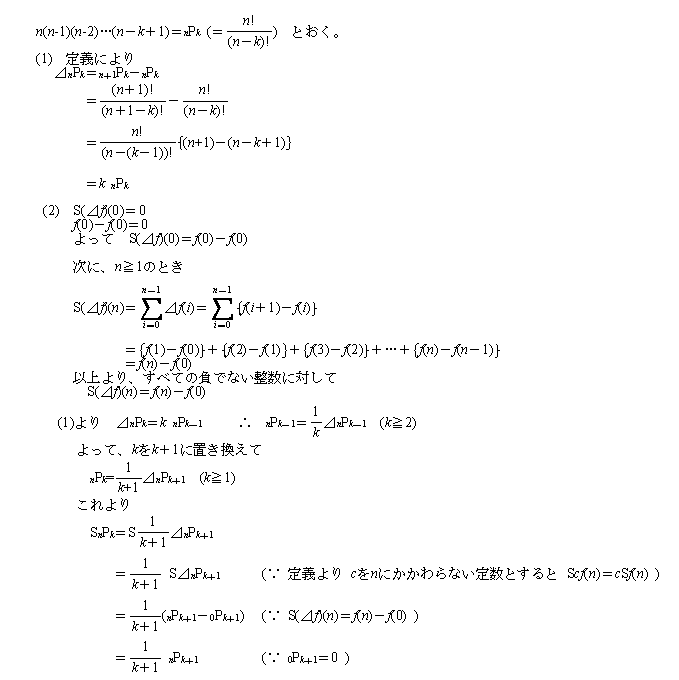
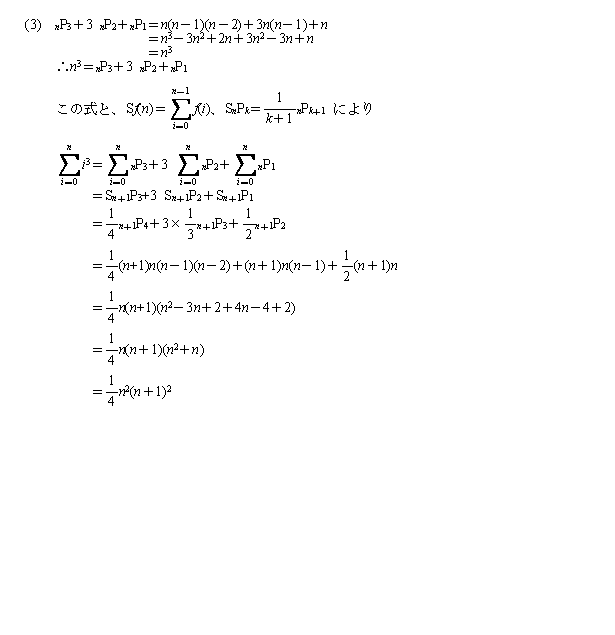

俶俷俀乽H7K乿偝傫 丂丂9/30:丂22帪06暘丂庴怣丂峏怴10/20
n^(k+壓慄)傪n**k偲彂偔偙偲偵偟傑偡丏
(1)delta(n**k)=(n+1)**k-n**k=(n+1)n(n-1)...(n-k+2)-n(n-1)...(n-k+1)
=k*n(n-1)...(n-k+2)=k*n**(k-1).//
(2)
S(delta f)(n)=f(n)-f(0)偲側傞偺偼丆偁傞堄枴柧傜偐丏
( S(delta f)(n)=sum(i=0 to n-1)(delta f)(i)=f(n)-f(n-1)+f(n-1)-f(n-2)+...-f(1)+f(1)-f(0)=f(n)-f(0).
)
偙傟傪梡偄傞偲丆
S((k+1)n**k)=S(delta (n**(k+1)))=n**(k+1)-0**(k+1)=n**(k+1).
椉曈傪k+1偱妱傝丆戣堄偺幃偑摫偐傟傞丏//
(3)
n**3+3*n**2+n**1=n(n-1)(n-2)+3n(n-1)+n=n(n-1)(n+1)+n=n(n^2-1)+n=n^3.
傛偭偰
sum(i=0 to n)i^3=sum(i=0 to
n)i**3+3*sum(i=0 to n)i**2+sum(i=0 to n)i**1
=S(n**3)+3S(n**2)+S(n**1)
=1/4*n**4+n**3+1/2*n**2
=1/4(n(n-1)(n-2)(n-3)+4n(n-1)(n-2)+2n(n-1) )
=1/4(n(n-1)(n^2-n-2)+2n(n-1))
=1/4(n(n-1)(n^2-n))
亙悈偺棳傟丗僐儊儞僩亜=偱傕丄=(n(n亄1)/2)^2.丂偵側傜側偄偐側丅(n(n-1)/2)^2.//
(4)丂摨條偵
sum(i=0 to n)i^4=S(n**4)+6S(n**3)+7S(n**2)+S(n**1)
=1/5*n**5+3/2*n**4+7/3*n**3+1/2*n**2
=1/30*(6n(n-1)(n-2)(n-3)(n-4)+45n(n-1)(n-2)(n-3)+70n(n-1)(n-2)+15n(n-1))
=1/30*(3n(n-1)(n-2)(n-3)(2n+7)+70n(n-1)(n-2)+15n(n-1))
=1/30*(n(n-1)(n-2)(6n^2+3n+7)+15n(n-1))
=1/30*n(n-1)(6n^3-9n^2+n+1)
=1/30*n(n-1)(2n-1)(3n^2-3n-1).//
戞擇庬僗僞乕儕儞僌悢偲偐偑偍傕偄偭偒傝巊偊傑偡傛偹....
亙悈偺棳傟丗僐儊儞僩亜偱傕偵丂=1/30*n(n亄1)(2n亄1)(3n^2亄3n乕1)丂側傜側偄偐側丅
戞擇庬僗僞乕儕儞僌悢偲偼丄傛偔抦偭偰偄傑偟偨偹丅巹偑戝岲偒側悢楍偱偡丅偳偙偐偺戝妛擖帋偵傑偨弌偰偙側偄偐側丅
俶俷俀乽H7K乿偝傫 丂丂9/30:丂23帪50暘丂庴怣丂峏怴10/20
偁丆側傫偩丆sum(i=0 to n-1)i^3偲偐傪媮傔偰偄偨傫偠傖側偄偐丏偁乕偁丆...
S(f(n))偑n-1傑偱側偺傪搑拞偱朰傟偰偄偨傛偆偱偡丏
偦偆偡傞偲丆偛巜揈偺偲偍傝偵側傝傑偡偹丏
怽偟栿偁傝傑偣傫丏
俶俷俁乽jun乿偝傫儕儞僋夝摎丂丂
俶俷係乽Kashiwagi乿偝傫10/06:16帪56暘丂庴怣丂峏怴10/20

俶俷俆乽15KARTSOUL乿偝傫10/11:11帪17暘 庴怣丂峏怴10/20丂丂
夝摎偱偡偑丆値丱(倠偺傾儞僟乕儔僀儞)傪丂値丱{倠}偲昞尰偝偣偰偄偨偩偒傑偡丅偱偼丅
(1)倠亞俀偺偲偒丆
丂儮値丱{倠}亖(値亄侾)丱{倠}亅値丱{倠}丂
丂丂丂丂丂亖(値亄侾)値(値亅侾)丒乧丒(値亄侾亅倠亄侾)
丂丂丂丂丂丂丂亅値(値亅侾)(値亅俀)丒乧丒(値亅倠亄俀)(値亅倠亄侾)丂
丂丂丂丂丂亖値(値亅侾)(値亅俀)丒乧丒(値亅倠亄俀)(値亄侾亅(値亅倠亄侾))
丂丂丂丂丂亖倠値(値亅侾)(値亅俀)丒乧丒(値亅(倠亅侾)亄1)
丂丂丂丂丂亖倠値丱{倠亅侾}
(2)値亞侾偺偲偒丆
丂丂丂丂丂丂丂 値亅侾丂丂値亅侾
丂俽(儮倖)(値)亖儼儮倖(倝)亖儼(倖(倝亄侾)亅倖(倝))
丂丂丂丂丂丂丂 倝亖侽 丂丂倝亖侽
丂丂丂丂丂丂亖倖(侾)亅倖(侽)亄倖(俀)亅倖(侾)亄倖(俁)亅倖(俀)亄乧亄倖(値)亅倖
(値亅侾)
丂丂丂丂丂丂亖倖(値)亅倖(侽)乧仢
傑偨丆値亖侽偺偲偒丆
丂嵍曈亖俽(儮倖)(侽)亖侽丆塃曈亖倖(侽)亅倖(侽)亖侽
傛傝丆惉棫丅
傑偨丆値亞侾偺偲偒丆
丂丂丂丂丂丂丂 値亅侾
丂俽(値丱{倠})亖儼 倝丱{倠}乧嘆
丂丂丂丂丂丂丂 倝亖侽
偲偙傠偱丆(1)偺寢壥傛傝丆
丂儮値丱{倠亄侾}亖(倠亄侾)値丱{倠}
丂値丱{倠}亖儮値丱{倠亄侾}乛(倠亄侾)
偙傟傛傝丆値亞侾偺偲偒丆
丂丂丂丂値亅侾丂丂丂丂丂丂丂丂丂丂丂丂値亅侾
丂嘆亖儼 (儮倝丱{倠亄侾}乛(倠亄侾))亖(儼 (儮i丱{倠亄侾}))乛(倠亄侾)
丂丂丂丂倝亖侽丂丂丂丂丂丂丂丂丂丂丂丂 倝亖侽
丂丂亖(俽(値丱{倠亄侾}))乛(倠亄侾)
丂丂 亖(値丱{倠亄侾}亅侽丱{倠亄侾})乛(倠亄侾)丂(仢傛傝)
丂丂 亖(値丱{倠亄侾})乛(倠亄侾)
値亖侽偺偲偒丆
丂嵍曈亖俽(侽丱{倠})亖侽丆塃曈亖(侽丱{倠亄侾})乛(倠亄侾)亖侽
傛傝惉棫丅
(3)塃曈亖値(値亅侾)(値亅俀)亄俁値(値亅侾)亄値
丂丂丂丂 亖値(値丱俀亅俁値亄俀亄俁値亅俁亄侾)
丂丂丂丂 亖値丱俁亖嵍曈
師偵丆
丂値丂丂丂丂値
丂儼 倝丱俁亖儼 (倝丱{俁}亄俁倝丱{俀}亄倝丱{侾})
丂倝亖侽丂丂倝亖侽
丂丂丂丂丂丂値丂丂丂丂丂 値丂丂丂丂丂丂値
丂丂丂丂 亖儼 (倝丱{俁})亄儼(俁倝丱{俀})亄儼(倝丱{侾})
丂丂丂丂丂丂倝亖侽丂丂丂 倝亖侽丂丂丂丂倝亖侽
丂丂丂丂 亖俽((値亄侾)丱{俁})亄俁俽((値亄侾)丱{俀})亄俽((値亄侾)丱{侾})
丂丂丂丂 亖((値亄侾)丱{係})乛係亄(値亄侾)丱{俁}亄((値亄侾)丱{俁})乛俀
丂丂丂丂 亖((値亄侾)丱{俀})乛係亊((値亅侾)(値亅俀)亄係(値亅侾)亄俀))
丂丂丂丂 亖(値(値亄侾))乛係亊(値丱俀亅俁値亄俀亄係値亅係亄俀)
丂丂丂丂 亖(値(値亄侾))乛係亊値(値亄侾)
丂丂丂丂 亖(値(値亄侾))丱俀乛係
(4)値丱係亖値丱{係}亄俇値丱{俁}亄俈値丱{俀}亄値丱{侾}傛傝丆
(3)偲摨條偵寁嶼偡傞偲丆
丂値丂丂丂丂
丂儼 倝丱係亖俽((値亄侾)丱係)
丂倝亖侽
丂丂丂丂 亖俽(値丱{係})亄俇俽(値丱{俁})亄俈俽(値丱{俀})亄俽(値丱{侾})
丂丂丂丂 亖((値亄侾)丱{俆})乛俆亄(俁(値亄侾)丱{俁})乛俀亄(俈(値亄侾)丱{俁})
乛俁亄((値亄侾)丱俀)乛俀
丂丂丂丂 亖((値亄侾)丱{俀})乛俁侽亊(俇(値亅侾)丱{俁}亄係俆(値亅侾)丱{俀}亄俈
侽(値亅侾)丱{侾}亄侾俆)
丂丂丂丂 亖(値(値亄侾))乛俁侽亊(俇値丱俁亄俋値丱俀亄値亅侾)
丂丂丂丂 亖(値(値亄侾)(俀値亄侾)(俁値丱俀亄俁値亅侾))乛俁侽
偆乣傫丆変側偑傜晄恊愗側夝摎偱偡丅丂崱夞偼偙偺曈偱偛姩曎傪丅丂丂
亙帺戭亜丂丂mizuryu@aqua.ocn.ne.jp
![]()
