平成14年11月23日
 [流れ星]
[流れ星]
第108回数学的な応募問題解答
<解答募集期間:11月3日〜11月23日>
[最大・最小となる点]
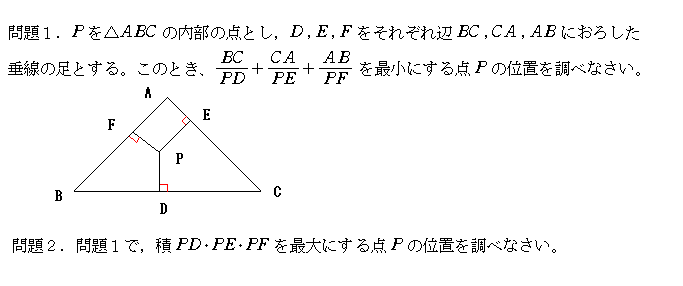
* 太郎さんは、数学Aの平面幾何を眺めていたところ、次のような問題をみつけました。皆さん、チャレンジください。
NO1「Kashiwagi」さん 11/5: 20時06分 受信 更新11/23
第108回解答
問1.
題意よりPD、PE及びPFの長さを各々x、y及びzとする。又、線分BC、CA及びABをa、b及びcと置く。
これより、BC/PD+CA/PE+AB/PF=a/x+b/y+c/zとなる。
ところで三角形ABCの面積は(ax+by+cz)/2であり、これはPの位置に拘わらず一定である。
そこで今、この一定値を求めるものにかけてみると(コーシーシュワルツの不等式にもっていけば解けるという勘です)、
(ax+by+cz)(a/x+b/y+c/z)となる。因ってこの値の最小値を求めれば良い。
(ax+by+cz)(a/x+b/y+c/z)
=a2 + b2 + c2 + ab(y/x
+ x/y)+ bc(y/z+ z/y)+ ca(x/z+ z/x)≧a2 + b2
+ c2 + 2ab+ 2bc+ 2ca
=(a + b + c)2
上記は相加相乗平均の関係から言える。因って、x=y=zの時最小値をとることが分かる。即ち、点Pが内心の場合である。
問2.
問1と同様に相加相乗平均の関係より
ax+by+cz≧33√abcxyzが成り立つ。
ここで問1の三角形の面積(ax+by+cz)/2をSとすると、
ax+by+cz=2Sであるから、ax=by=czである点Pがとれればxyzの最大値は 8S3/(27abc)
次に線分CPを延長し、ABとの交点をDとし、∠BCD=X、∠ACD=Y、∠ADC=Z、∠BDC=Wとし三角形ADCと三角形CDBに正弦定理を適用すると、
AD/DB=bsinY/a sinX
=by/CP/ax/CP = by/ax が成り立つ。
即ち、AD=DBとax=byは同値である。これよりax=byとPがCからの中線上の点である事が同値である。
全く同様にしてax = czとPがBからの中線上の点である事が同値である。
これよりax=by=czとPが三角形ABCの重心であることが同値である。
NO2「浜田」さん 11/6:12時22分 受信
<水の流れ:浜田さんから受信した回答は、帰納的な考えで、点Pを動かして、与えられた式が最小・最大なる点を探して、見つけています。
ところが、現在もこの動画をブラウザ上に載せるだけの技量を持ち合わせていません。お許しください。>
NO3の1「スモークマン」さん
11/5:21時52分 受信 更新11/23
AB/PD+BC/PE+AC/PF≧3立方根(AB*BC*AC/PD*PE*PF)
よって、PD*PE*PFが最大の時、左辺は最小となる。
AB*PD+AC*PE+CA*PF=2△ABC≧3立方根(AB*AC*CA*PD*PE*PF)
だから、PD*PE*PFの最大値は、等号が成立するときで、
AB/PD=AC/PE=CA/PFの時。
でも、それがどんな点か分かりません。
NO3の2「スモークマン」さん
11/6:22時09分 受信 更新11/23
1.考えました。
垂心から、それぞれの辺に下ろした点をD'.E',F'とするとき、BC/PD+CA/PE
≧BC/SD'+CA/SE'
BC/PD+AB/PF≧BC/SD'+AB/SF'
CA/PE+AB/PF≧CA/SE'+AB/SF'
これらは、Pを通る各辺の平行線とAD',BE',CF'との交点を考え
れば、成り立つのは明らか。
両辺をそれぞれ足すと、BC/PD+CA/PE+AB/PF≧BC/SD'+CA/SE'+AB/SF'
となるから、左辺の最小値は、PがS(垂心)のとき!
<水の流れ:残念ながらこちらのとはあっていません。ナイスチャレンジでしたが。>
2.AB*PF+BC*PD+CA*PE=2△ABC( 一定
)≧3(立方根)AB*BC*CA*PF*PD*PE
から、AB*BC*CA=一定 なので、PD*PE*PFの最大値は、AB*PF=BC*PD=CA*PE
<水の流れ:こちらは正解です。でも、AB*PF=BC*PD=CA*PE のとき、Pが、重心のときとなることを示して欲しいです>
NO3の3「スモークマン」さん
11/8:18時00分 受信 更新11/23
分かりました。ありがとうございます。
2.AB*PF+BC*PD+CA*PE=2△ABC( 一定 )≧3(立方根)AB*BC*CA*PF*PD*PE
から、AB*BC*CA=一定 なので、PD*PE*PFの最大値は、AB*PF=BC*PD=CA*PE
のときで、これらは、△ABCを1/3にすることと同じ。
また、各頂点から、対辺の中点を結んだ線の交点(重心)を考えるとき、それらの線分で分けられた6つの三角形の面積はすべて等しいことより(※)、
重心は求める点Pの条件を満たしていることが分かる。(※)中線で分けられる6つの三角形は、a,a,b,B,C,Cとなるが、2a+b=2c+bとなっているので、a=b=cである。
1.BC/PD+CA/PE+AB/PF≧3(立方根)BC/PD*CA/PE*AB/PF
から、BC/PD=CA/PE=AB/PFのとき。
これは、各頂点からの角の2等分線上の点で、その交点なら成
り立つ。この点の名前は何だったかわかりませんが・・・。
<水の流れ:そうですね。この点は三角形の内心といいます。>
NO4「toru」さん 11/12:15時06分 受信 更新11/23
たまたま問題を見つけて、試みに考えてみました。せっかくですから解答を送らせて
頂きます。どうかお手やわらかにお願いします。 Toru
問題1
BC/PD+CA/PE+AB/PF
=(FA/PF+AE/PE)+(EC/PE+CD/PD)+(BD/PD+BF/PF)
ここで角PAF=θとすると
FA/PF+AE/PE=cosθ/sinθ+cos(A-θ)/sin(A-θ)=F(θ) (0<θ<A)とこれは
θの関数となる。ここでF'(θ)= -1/(sinθ)^2 +1/(sin(A-θ)^2) ま
た0<A<πだから、F(θ)は0<θ<A/2 で単調減少、A/2<θ<Aで単調増加となりθ=A/2で
最小となることが分かる。EC/PE+CD/PD、BD/PD+BF/PFについても同様であるの
で、BC/PD+CA/PE+AB/PFはPが角A、B、Cそれぞれの2等分線の交点(これは存在
して)三角形ABCの内心にある時、最小となる。
問題2
APを延長して、BCとの交点をGとするまたBG:GC=x:1-x, AP:PG=y:1-y とす
る(0<x<1,0<y<1)。また三角形ABCの面積をS、辺BC,CA,ABをそれぞれa、b、cとすると
(PD/(1-y))・a/2=S ,(PE/y)・b/2=(1-x)・S, (PF/y)・c/2=x・Sが成り立つ。
これからPD・PE・PF=8S^3/abc・(x-x^2)(y^2-y^3)
G(x)=x-x^2 とするとG'(x)=1-2x, H(y)=y^2-y^3とするとH'(y)=(2-3y)y
これらからPD・PE・PFはx=1/2,y=2/3の時、すなわちPが三角形ABCの重心にある時、
最大となることがわかる。
NO5「ニースケンス」さん 11/13:19時06分
受信 更新11/23

NO5「三角定規」さん 11/15:10時57分
受信 更新11/23

![]()
