平成１５年１月１５日

[流れ星]

　　　　　　　　第１１１回数学的な応募問題解答

　　　　　　　　　　＜解答募集期間：１月１日〜１月１５日＞

［tanのｎ倍角］

　　　

＊　太郎さんは、先日生徒から、「三角関数のsin3θをsinθ、 cos3θ をcosθ　で表す３倍角の公式があるのに、tan3θを
tanθで表す公式はないのですか。あれば、教えてください。」という質問を受けました。そのときは、私の見たことがないから、「必要なら、自分で作ったら。」。と言っておきました。このことを、問題にします。tanθ＝ｔ　とおくとき、次の設問に答えてください。

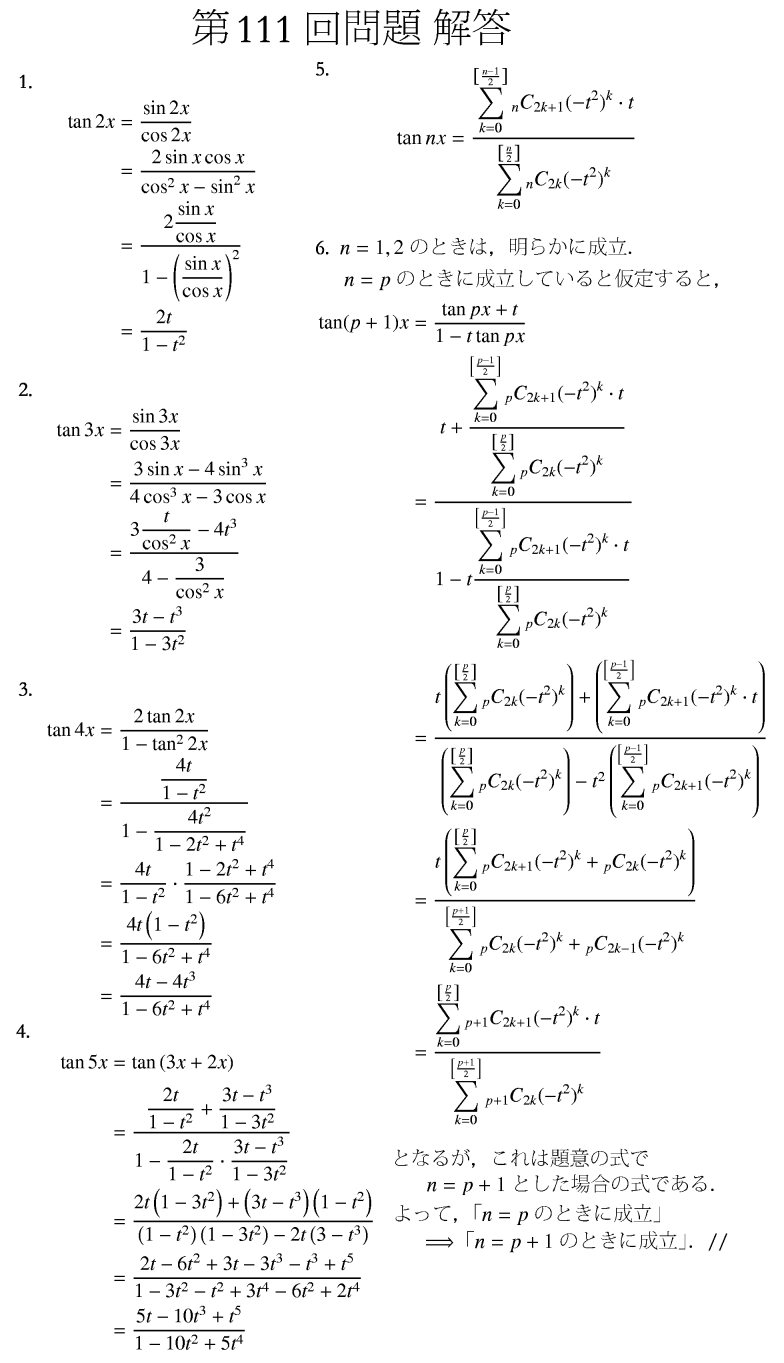
（１）tan2θをｔで表せ。（これは公式ですから、結果だけでいいです。）

（２）tan3θをｔで表せ。

（３）tan4θをｔで表せ。

（４）tan5θをｔで表せ。

（５）今までの答えから、類推して、tanｎθをｎとｔで表せ。

（６）（５）の予想が正しいことを数学的帰納法で示してください。

追加（７）実はこの計算をしていたら、分母、分子の係数が有名な数列になっていることに気がつきました。必然性があるのでしょうか。

疑問に思っています。どなたか　教えてください。

NO1「H7K」さん 　　 12/31:　21時10分　受信　更新1/15
「H7K」さん 　　 1/2 :　09時15分　受信　更新1/15

NO2「Kashiwagi」さん 1/4 : 17時31分　受信　更新1/15

第111回解答

(1)2t／1−t²

(2)tan3θ＝tan(θ＋2θ)＝〔tanθ＋tan2θ〕／1− tanθ･tan2θであるからtanθ＝ｔとtan2θ＝2t／(1−t²)を代入し、3t− t^３／1−3t²が求めるもの。

(3)上記と全く同様な計算を行い、4t− 4t³／1−6t²＋t⁴

(4)上記と全く同様な計算を行い、5t− 10t³＋t⁵／1−10t²＋5t⁴

(5)分子と分母を一緒にして、θ、2θ、3θ、4θ及び5θを見ていくと、ｔの係数はｎθのｎである。

又、t²　の係数は階差数列が初項2、公差1の等差数列であることから、計算し、−ｎ(ｎ−1)／2（＝−_ｎC_２）を得る。

t³以下についても同様な考察より、−ｎ(ｎ−1) (ｎ−2)／2･3（−_ｎC₃）、即ち組み合わせの数となる。

因って、係数の正負に注意して整理すると、

�@ ｎが偶数の時

_ｎC₁ｔ−_ｎC₃ t^３＋……・・・・＋(−1)^{ｎ−２/２}_ｎC_ｎ−１ t^ｎ−１／1−_ｎC₂ｔ²＋_ｎC₄ t⁴＋……・・・＋(−1)^ｎ/２_ｎC_ｎ t^ｎ

�A ｎが奇数の時

_ｎC₁ｔ−_ｎC₃ t^３＋……・・・・＋(−1)^{ｎ−１/２}_ｎC_ｎ t^ｎ／1−_ｎC₂ｔ²＋_ｎC₄ t⁴＋……・・・＋(−1)^{ｎ−１/２}_ｎC_ｎ−１ t^ｎ−１

となる。　　　

(6)今を考える。ｋ＝1の時_１C₁ｔ／１＝ｔとなり成立する。次にｋ＝ｎ（ｎは偶数とする）の場合に成立するとすると、

tanｎθ＝_ｎC₁ｔ−_ｎC₃ t^３＋……・・・・＋(−1)^{ｎ−２/２}_ｎC_ｎ−１ t^ｎ−１／1−_ｎC₂ｔ²＋_ｎC₄ t⁴＋……・・・＋(−1)^ｎ/２_ｎC_ｎ t^ｎ

これを使い、tanθ＋tanｎθと１−tanθtanｎθを計算すると、各々

(1＋_ｎC₁)ｔ−(_ｎC_２＋_ｎC₃)t^３＋……・・・＋(−1)^ｎ/２_ｎC_ｎt^ｎ＋１／1−_ｎC₂ｔ²＋_ｎC₄ t⁴＋……・・・＋(−1)^ｎ/２_ｎC_ｎ t^ｎ

及び

１−(_ｎC_１＋_ｎC_２)t^２＋……・・・・＋〔(−1)^{ｎ−２/２}_ｎC_ｎ−１＋(−1)^ｎ/２_ｎC_ｎ〕t^ｎ／1−_ｎC₂ｔ²＋_ｎC₄ t⁴＋……・・・＋(−1)^ｎ/２_ｎC_ｎ t^ｎ

　となる。

ここでtanθ＋tanｎθ／１−tanθtanｎθを計算すると、

(1＋_ｎC₁)ｔ−(_ｎC_２＋_ｎC₃)t^３＋……・・・＋(−1)^ｎ/２_ｎC_ｎt^ｎ＋１／１−(_ｎC_１＋_ｎC_２)t^２＋……・・・・＋〔(−1)^{ｎ−２/２}_ｎC_ｎ−１＋(−1)^ｎ/２_ｎC_ｎ〕t^ｎ

となる。

1＋_ｎC₁＝_ｎ＋１C₁、_ｎC_２＋_ｎC₃＝_ｎ＋１C₃を使い上式を変形すると、

_ｎ＋１C₁ｔ−_ｎ＋１C₃ t^３＋……・・・・＋(−1)^ｎ/２_ｎ＋１C_ｎ＋１ t^ｎ＋１／1−_ｎ＋１C₂ｔ²＋_ｎ＋１C₄ t⁴＋……・・・＋(−1)^ｎ/２_ｎ＋１C_ｎ t^ｎ

＝tan(ｎ＋１)θとなる。因ってtanｎθが上記の形で表されることが証明された。

ご指摘の様に非常に興味深い結果となりました。これまで、考えたこともありませんでした。

どなたかのお教えを楽しみに待たせて頂きます。

NO3「三角定規」さん　 1/4 : 23時40分 受信　更新1/15

<感想>・泥くさい加法定理の計算から始まって，A4版の用紙で10枚ほどの計算をしました。どうやら二項係数が出て来ているようだと気がついてからも，この行列にたどり着くまでに，行きつ戻りつしました。この一太郎で数式を打ち込むのがえらく大変なため，上記は，そのエッセンスのみです。・加法定理を習ってから20余年，加法定理と二項係数がこんな関わりをもっていたとは………。

NO4「浜田」さん　　　 1/6 :　13時01分　受信　更新1/15

tanθ＝ｔから，
　　tan２θ＝sin２θ／cos２θ
　　　　　 ＝２sinθcosθ／{(cosθ)^2−(sinθ)^2}
　　　　　 ＝(２sinθ／cosθ)／{１−(sinθ／cosθ)^2}
　　　　　 ＝２tanθ／{１−(tanθ)^2}
　　　　 　＝２ｔ／(１−ｔ^2)………(1)
　　tan３θ＝tan(２θ＋θ)
　　　　　 ＝(tan２θ＋tanθ)／(１−tan２θtanθ)
　　　　　 ＝{２ｔ／(１−ｔ^2)＋ｔ}／{１−２ｔ／(１−ｔ^2)・ｔ}
　　　　　 ＝ｔ{２＋(１−ｔ^2)}／{(１−ｔ^2)−２ｔ^2}
　　　　　 ＝ｔ(３−ｔ^2)／(１−３ｔ^2)………(2)
　　tan４θ＝tan(３θ＋θ)
　　　　　 ＝(tan３θ＋tanθ)／(１−tan３θtanθ)
　　　　　 ＝{ｔ(３−ｔ^2)／(１−３ｔ^2)＋ｔ}／{１−ｔ(３−ｔ^2)／(１−３ｔ^2)・ｔ}
　　　　　 ＝ｔ{(３−ｔ^2)＋(１−３ｔ^2)}／{(１−３ｔ^2)−ｔ^2(３−ｔ^2)}
　　　　　 ＝ｔ(４−４ｔ^2)／(１−６ｔ^2＋ｔ^4)
　　　　　 ＝４ｔ(１−ｔ^2)／(１−６ｔ^2＋ｔ^4)………(3)
　　tan５θ＝tan(４θ＋θ)
　　　　　 ＝(tan４θ＋tanθ)／(１−tan４θtanθ)
　　　　　 ＝{４ｔ(１−ｔ^2)／(１−６ｔ^2＋ｔ^4)＋ｔ}／{１−４ｔ(１−ｔ^2)／(１−６ｔ^2＋ｔ^4)・ｔ}
　　　　　 ＝ｔ{４(１−ｔ^2)＋(１−６ｔ^2＋ｔ^4)}／{(１−６ｔ^2＋ｔ^4)−４ｔ^2(１−ｔ^2)}
　　　　　 ＝ｔ(５−１０ｔ^2＋ｔ^4)／(１−１０ｔ^2＋５ｔ^4)………(4)
　　tan６θ＝tan(５θ＋θ)
　　　　　 ＝(tan５θ＋tanθ)／(１−tan５θtanθ)
　　　　　 ＝{ｔ(５−１０ｔ^2＋ｔ^4)／(１−１０ｔ^2＋５ｔ^4)＋ｔ}／{１−ｔ(５−１０ｔ^2＋ｔ^4)／(１−１０ｔ^2＋５ｔ^4)・ｔ}
　　　　　 ＝ｔ{(５−１０ｔ^2＋ｔ^4)＋(１−１０ｔ^2＋５ｔ^4)}／{(１−１０ｔ^2＋５ｔ^4)−ｔ^2(５−１０ｔ^2＋ｔ^4)}
　　　　　 ＝ｔ(６−２０ｔ^2＋６ｔ^4)／(１−１５ｔ^2＋１５ｔ^4−ｔ^6)
　　　　　 ＝２ｔ(３−１０ｔ^2＋３ｔ^4)／(１−１５ｔ^2＋１５ｔ^4−ｔ^6)
　　・・・

　

　

NO5「toru」さん　　　 1/7 : 12時57分 受信　更新1/15

あけましておめでとうございます。本年もよろしくお願いします。年明け早々なかな
か面白い問題で楽しませて頂きありがとうございます。（７）はいろいろ考えてみま
したが期待に沿うような答かどうか？　ペンネーム　Ｔｏｒｕ

第１１１回解答
tan (n+1)θ=sin (n+1)θ／cos (n+1)θ=(sin nθcosθ+sinθcos nθ)／（cos nθcosθ-sin nθsinθ）=(tan nθ+tanθ)／(1-tan nθtanθ)---------a)
これより(1) n=1 としてtan2θ=2t／(1-t^2)
(2) tan3θ=(tan2θ+tanθ)／(1-tan2θtanθ) =(3t-t^3)／(1-3t^2)（(1)を代入）
(3) tan4θ=(tan3θ+tanθ)／(1-tan3θtanθ)=(4t-4t^3)／(1-6t^2+t^4)
(4) tan5θ=(tan4θ+tanθ)／(1-tan4θtanθ)=(5t-10t^3+t^5)／(1-10t^2+5t^4)
(5)これらからtan nθ=(nC1 t-nC3 t^3+nC5 t^5----)／（1-nC2 t^2+nC4 t^4----）と考える。
ただしn<kの時nCk =０とする。
(6) (5)式をa)に代入しn+1Ck=nCk+nCk-1に注意して計算すると、
tan(n+1)θ=　((1+nC1)t-(nC2+nC3)t^3+(nC4+nC5)t^5---)／（1-(nC1+nC2)t^2+(nC3+nC4)t^4---）
= (n+1C1 t-n+1C3 t^3+n+1C5 t^5---)／（1-n+1C2 t^2+n+1C4 t^4-----）と
n+1の時も成り立つことが示された。
(7) 分母分子の係数は、＋、―を除いて、tan1θ=t／1とすれば1,1、1,2,1、1,3,3,1、1,4,6,4,1、1,5,10,10,5,1といった具合に
２項定理の係数（縦にならべればパスカルの三角形）となっています。
（(5)で予想した時にもちろんこれを使っているのですが）
これはe^ (iθ)=cosθ+ ｉsinθの両辺をn乗してe^(ｉnθ)=cos nθ+ｉsin nθ=(cosθ+ｉsinθ)^n ---b)
の右辺を２項展開して虚数項と実数項にわけると
(cosθ+ｉsinθ)^n =ΣnCk(cosθ)^(n-k)(ｉsinθ)^k
　　　　　　　　　　　=(cosθ^n) ΣnCk(ｉt)^k
　　　　　　　　　　 　=(cosθ^n) （ΣnC2k(ｉt)^2k+ΣnC2k+1(ｉt)^(2k+1)）
　　　　　　　　　　　=(cosθ^n) （Σ(-1)^k nC2k
t^2k+ｉΣ(-1)^k nC2k+1 t^(2k+1)）実数項がcos nθ、虚数項がsin nθであるから
tan nθ=sin nθ／cos nθはcosθ^nが約分されて、
（Σ(-1)^k nC2k+1 t^(2k+1)）／(Σ(-1)^k nC2k t^2k)　(k=0,1,2,----)
となって分子が(1+t)^nを二項展開したときの奇数乗項、分母が偶数乗項（ただし+,-交互）となることがわかる。
なお
　b)とcos nθ-ｉsin nθ=(cosθ-ｉsinθ)^n から
2cos nθ=(cosθ+ｉsinθ)^n+(cosθ-ｉsinθ)^n , 2ｉsin nθ=(cosθ+ｉsinθ)^n-(cosθ-ｉsinθ)^n
よりtan nθ=((cosθ+ｉsinθ)^n-(cosθ-ｉsinθ)^n)／((cosθ+ｉsinθ)^n+(cosθ-ｉsinθ)^n)ｉ
　　　　　　　=((1+ｉt)^n-(1-ｉt)^n)／((1+ｉt)^n+(1-ｉt)^n)ｉという表わしかたも可能と思います。

NO６「udonko」さん　　　 1/13 : 02時08分 受信　更新1/15

はじめまして、udonkoと申します。
いろいろとネットを見ていたら、ここにたどり着きました。
最初はちょっとだけ考えてみようと思ったのですが・・・・非常に難しいですね。

どのようにメールで送れば良いのかわからないので
こんな解答で、ごめんなさい。（解答になってませんね〜）＾＾；

　　　　  　nC1*t-nC3*t^3+nC5*t＾5-nC7*t^7+・・・・・・　
tan(nθ)＝＿＿＿＿＿＿＿＿＿＿＿＿＿_________＿＿＿
　　　　　　nC0-nC2*t^2+nC4*t^4-nC6*t^6+・・・・・・

になりました。

帰納法による証明も　nCk+nC(k+1)=(n+1)C(k+1) を使ってできると思います。
（nCn*t^nの項が、分母にあるか分子にあるか、場合わけしないと・・・・・
ちゃんとやっていなくてすいません）

2項定理の展開した形で、分母が偶数乗の項、分子が奇数乗の項
に別れているのが美しいですね。（符号を無視していますが・・・）

＜水の流れ：コメント＞全員の方が、解答を作成するのに、多くの時間をかけておられて、大変恐縮しています。
「H7K」さんには、画像をgifで送信くださいまして感謝しています。
また、ｎが奇数、偶数をガウス記号［　　］で「H7K」さんと「三角定規」さんはうまく表現してありました。
さらに、n+1Ck=nCk+nCk-1を利用して　数学的帰納法で証明されていましたし、「Ｔｏｒｕ」さんは、複素数を用いての解答は数学って本当に自由性があるんだなーと実感させられました。
tan nθ=((cosθ+ｉsinθ)^n-(cosθ-ｉsinθ)^n)／((cosθ+ｉsinθ)^n+(cosθ-ｉsinθ)^n)ｉ
　　　　　　　=((1+ｉt)^n-(1-ｉt)^n)／((1+ｉt)^n+(1-ｉt)^n)ｉ　はどこかで利用できないかなと思います。
「Kashiwagi」さん「浜田」さんの解答には、表現方法に苦労の後が感ぜられます。
「udonko」さんは、初めての参加でしたが、これからもよろしくお願いします。
受験生に、tanのｎ倍角の公式も作れば出てくることを知ってもらいたいです。

　　　　＜自宅＞　　mizuryu@aqua.ocn.ne.jp