平成１２年１月３０日

［正2ｎ角形］

１月31日に、「sambaGREEN」さんから、『「正ｎ角形」となっていますが，例をみると，「正２ｎ角形ですね」正２ｎ角形として，解答します。』とご指摘がありましたので、修正しました。

　太郎さんは、円に内接している正２ｎ角形を描いています。この図形の頂点をｎ組のペアに分ける方法の中で、

それぞれのペアを結ぶｎ本の線分が互いに交わらないように分ける方法を考えてみました。

この分け方の方法をｆ(n)としたとき、次の問題に答えてください。

　ただし、ｆ(０)＝１，　ｆ(１)＝１と便宜上します。

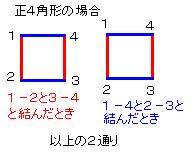
また、ｎ＝２ときは参考に図に書いておきます。ここから、ｆ(２)＝２になっています。

問題１：ｎ＝３，４のとき、ｆ(n)を求めてください。

問題２：ｆ(n)の漸化式を作って、一般項ｆ(n)をｎで表してください。

　太郎さんは、早速、正６角形や。正８角形を描いて考えてみようと思っています。

ＮＯ１　＜sambaGREEN＞さんからの解答　1/31　０時47分受信、　2/4 更新　　　

「正ｎ角形」となっていますが，例をみると，「正２ｎ角形ですね」

正２ｎ角形として，解答します。

***********************************

【問題１】

ｎ＝3のとき，６個の頂点に１〜６の番号をふると，１と結べるのは，2,4,6。

　２，６と結ぶとき，２通り。　４と結ぶとき，1通り。

　f(3)＝２＋１＋２＝５

ｎ＝４のとき，８個の頂点に１〜８の番号をふると，１と結べるのは，2,4,6,8

　２，８と結ぶとき，f(3)通り。　４，６と結ぶとき，f(1)*f(2)通り。

　f(4)＝f(3)*2＋f(2)*f(1)*2＝5*2＋2*1*2＝14

【問題２】

2ｎ個の点に１から2ｎまで番号をつけます。１と結べるのは２i（i=１〜ｎ）

１と2iを結んだとき，残りの頂点は，2(i-1)個と2(n-i)個に分けられるので，

f(n)＝f(0)*f(n-1)＋f(1)*f(n-2)＋・・・＋f(i-1)*f(n-i)＋・・・＋f(n-2)*f(1)＋f(n-1)*f(0)

f(n)はカタラン数。よって，f(n)＝2nＣn/(n+1)

**************************************

【追伸】

ヒントが大き過ぎました（私にとっては）。

私が，「水の流さん」を知ったのは，青木先生の「数学の部屋」です。

恥ずかしながら，それまで，「カタラン数」についてあまり知らなかったのです。

「カタラン数についての研究レポート」を読ませていただいたのが，

ＨＰにお邪魔させていただくきっかけでした。というわけで，

私の脳の中では，「水の流れさん」≡「有名な数列」≡「カタラン数」です。ハイ。

＜水の流れ＞　２月４日記入

光栄なお言葉ばかりでして、嬉しいかぎりです。読者の皆さんはありがたいです。感謝します。

これからの、張り切って応募問題を連載していきます。次回は、大統領選挙を考えています。

ＮＯ２＜ch3cooh＞さんからの解答　２/3　16時53分受信、　2/4 更新

考え方として、正2n角形のある一点に注目し、その隣の点で円上から

直線に展開すると、"線が交わらない"という条件が一致するからです。