平成１２年８月２日

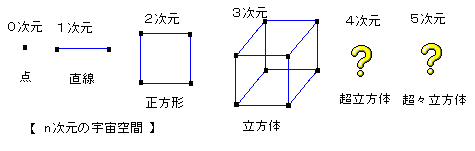
［ｎ次元宇宙空間］

　太郎さんは、ときどき　夜空を見上げて、果てしなく続く宇宙空間を眺めています。

このとき、０次元の世界に住んでいると、そこには点の世界だから、境界はひとつ「頂点」があるだけです。

この点を動かしてみると、１次元の世界ができあがるが、ここには「線」でしかない。これには、「境い目」が２つある。

その両端である。言いかえれば、「２つの０次元境界（頂点）と１つの１次元境界（線）とがある」と言える。

　さて、この直線を横にその長さだけ引っ張ると、正方形ができる。すると、頂点の数は、以前あった２から４に倍増している。

また、正方形では４つの直線、つまり辺が４本あり、さらに、１枚の２次元境界（面）がここではじめて出てくる。

　さて次ぎに、２次元の平面から上に向かって離れていくと、例えば、正方形を上にうまく移動すれば、立方体を作ることができ

る。４つの頂点の動いた軌跡がまず４本の線を作りだすから、辺は１２本、頂点は８個、面は２次元では、１枚しかなかったが、

一挙６枚になっている。

これを、繰り返して、４次元の超立方体、５次元の超々立方体、・・・。ｎ次元の超々々・・・立方体を考えていきます。

ここには、ｎ次元空間の世界があるのです。

このときの０次元境界（頂点）、１次元境界（辺）、２次元境界（面）、３次元境界（立体）、・・・、（ｎ―１）次元境界

（名前はまだできていない）の数を調べたいのです。ここには、オイラーの多面体定理が成り立つと思っていますが、・・・・

何せ、頭の中でしか想像できない超々々・・・立方体ですので、困っています。

ここで、問題です。

問題１：４次元の「超立方体」には境界になる、点、辺、面、立体がそれぞれいくつあるでしょう。

問題２：一般に、ｎ次元の「超々々・・・立方体」には境界になる、点、辺、面、立体、・・・、（ｎ―１）次元境界の数は

一体いくつあるでしょう。一般式が求められています。皆さん考えてください。

＜ヒント：群数列でみると、（１）、（１，２）、（１，４，４）、（１，６，１２，８）、・・・・＞

　ＮＯ１＜ch3cooh＞さんからの解答です。２０日の１０時９分受信　、３０日更新

かなり難しい問題ですね？ディジタル信号のエラー訂正に使用される

ガウス空間上の隣接点の概念で良く似たことについて 考察されています。

回答ですが、まだ完全には出来ていません。

考え方として・・・

N 次元空間上の点の位置として

(±1,±1,±1,・・・) とすると 点の数は 2^N

線は、各点に隣接する点までに引いたものなので

2^N * N / 2

(点の数 * 次元の数(隣接する点は次元の数だけある) / 2重にカウントされた分 )

これを拡張していくと ・・・

面の数

2^N * N * (N-1) / (2^2 * 2!)

立方体の数 ???

2^N * N * (N-1) * (N-2) / (2^3 * 3!)

n次元体

2^N * N! / ((N-n)! * 2^n * n!)

＜水の流れ＞コメント：私のこれが良いのか分かりませんが、誰か、コメントを。３０日記入

ＮＯ２＜satoshi＞さんからの解答です。２９日の２３時２４分受信　、３０日更新

４次元のものは、点＝16　辺＝32　面＝24　立体＝8

まず,点の数については、１つの点からもうひとつ点が出てくるため,

点の数＝2＾ｎ

つぎに辺の数は,もともとあった辺が２倍になり,

各点から１本ずつ出ている為,

もともとあった辺の数*2+2＾（n−1）

面の数も同じように各辺から1面ずつ出る

立体の数も同じように。

これをまとめると,

ｎ次元のm次元境界の数は,

n−1次元の｛（m−1次元境界の数）-1｝+2（m次元境界の数）｝となる。

以上。

もうちょっとわかりやすくできそうな気がしますが,

まだ中学生ってことで,大目に見て下さい。

＜水の流れ＞コメント：なかなかどうして、中学生にとって、ｎ次元の「超々々・・・立方体」が想像がつかないのに

よく考えられましたね。驚嘆します。正解です。ただ、、気になっているのが、

「ｎ次元のm次元境界の数は,

n−1次元の｛（m−1次元境界の数）-1｝+2（m次元境界の数）｝となる。」ところです。

ここは、｛（m−1次元境界の数）｝+2（m次元境界の数）｝ではないですか。

ＮＯ３＜Footmark＞さんからの解答です。３０日７時４７分受信　更新３０日

　青木先生の「数学の部屋」の掲示板から、こちらに初めてやって来ました。

やって来たら、なんと締切が今日でした。（掲示板で分かっていれば、もっと早く来たのに・・）

時々、訪問させて頂きますがよろしくお願いいたします。

「ｎ次元の宇宙空間」の解答

超超超・・・立方体と言うのも、しまいには超が幾つあるのか分からなくなるので便宜的に次のように呼ばせて頂きます。

点　　　：０次体

辺　　　：１次体

面　　　：２次体

立体　　：３次体

超立体　：４次体

超超立体：５次体

・

　　　　　　：(ｎ−１)次体

：ｎ次体

(ｎ−１)次元の(ｎ−１)次体を、さらに新しい独立したｎ番目の次元の方向に延長させてｎ次元のｎ次体を１つ作成させると、

ｎ次体に含まれる(ｋ−１)次体の数は、(ｎ−１)次元にあった(ｋ−１)次体が新しいｎ次元方向にもコピーされその数は

２倍となり、さらに(ｎ−１)次元にあった(ｋ−２)次体からその数だけｎ次元での(ｋ−１)次体が新しく生じる。

(ただし １≦ｋ≦ｎ)

また、ｎ次体に含まれる０次体の数は、(ｎ−１)次元にあった０次体が新しいｎ次元方向にもコピーされその数は２倍となる。

これを順次解くと,

ｎ次元内のｋ次体の数 ＝ nＣk*２**(ｎーｋ)

(ただし ０≦ｋ≦ｎ)

問題１：

点の数　 ＝ ０次体の数 ＝ 4Ｃ0*２**(４ー０) ＝ １ * １６ ＝ １６

辺の数　 ＝ １次体の数 ＝ 4Ｃ1*２**(４ー１) ＝ ４ * 　８ ＝ ３２

面の数　 ＝ ２次体の数 ＝ 4Ｃ2*２**(４ー２) ＝ ６ * 　４ ＝ ２４

立体の数 ＝ ３次体の数 ＝ 4Ｃ3*２**(４ー３) ＝ ４ * 　２ ＝ 　８

問題２：

　　　　ｎ次元内のｋ次体の数 ＝ nＣk*２**(ｎーｋ)

　　　　　(ただし ０≦ｋ≦ｎ)＞

＜水の流れ＞コメント：今回のご応募ありがとうございます。よく、考えられましたね。

このように、数学は考えてみると、楽しくなり、真理を追究することができます。

まだまだ、多くの神秘が隠されていますので、次回も、挑戦をお願いします。

そうですね、すべて正解です。鮮やかに解かれまいたね。

そして、ｎ次元の場合もです。そこで、

（２＋ｘ）＾０，（２＋ｘ）＾１、（２＋ｘ）＾２，（２＋ｘ）＾３，（２＋ｘ）＾４、　・・・、（２＋ｘ）＾ｎ

を展開ください。この係数がすべての、次元の境界の数を表していますし、

ｘ＝ー１を代入したら、オイラーの多面体公式が拡張が現れてきますかな。

これ、私の発見ですけど。れからも、よろしくお願いします。

ＮＯ４＜satoshi＞さんからの解答です。３１日の２０時０３分受信　、８月２日更新

先生のおっしゃるとおり、ｎ次元のm次元境界の数は,n−1次元の｛（m−1次元境界の数）-1+2（m次元境界の数）｝となるではなく、

｛（m−1次元境界の数）+2（m次元境界の数）｝となります。自分でもなんでこんなこと書いたのかわからないです・・・・疲れてたかな？

それはそれでいいとして、ｎ次元の世界について,自分なりに考えてみました。

ホームページの問題では,点や,線を引っ張っていましたが,

僕は,学校の校長先生に

　点がひとつだと何もできないが,

　点が二つになると,線ができる。

　点が三つになると,面ができる。

といった話を聞いたことがあり、

この話を発展させて,点が４つになると,立体ができる。（四面体）

じゃあ,点が５つあれば,そこに４次元空間ができるのではないかと考えました。

この場合、ｎ次元の,m次元境界の数は,ｎ−1次元の｛（m−1次元境界の数）｝+（m次元境界の数）｝になります。

この式を使って次元境界の数を具体的に計算すると、次のようになりました。

次元　　　　　　点　　　辺　　　　面　　　　立体　　　４次元境界　　５次元境界
　0　　　　　　　1　
　1　　　　　　　2　　　1　
　2　　　　　　　3　　　3　　　　　1
　3　　　　　　　4　　　6　　　　　4　　　　　1　
　4　　　　　　　5　　　10　　　　10　　　　　5　　　　　　　1
　5　　　　　　　6　　　15　　　　20　　　　　15　　　　　　　6　　　　　　　　1

この数を見ると,パスカルの三角形になっていることがわかります。

また,この方法では,４次元空間が想像しやすく

四面体の中に，１点をとってやり,その点から各点に線を引いてやると

１つの四面体が４つの四面体に分かれて，

点は５、辺は１０、面も１０、そして立体は，4+1（全体で1つ）で，５になります。

（1つの四面体の空間の中に，4つの四面体の空間があることになる）

3次元空間に，4次元空間の元となる形が作れました。

この点を，４次元の軸の方向に移動させれば

（移動させると3次元の空間から消えてしまう）

4次元空間の出来上がりということになります。

これくらいなら，別に，普通の中学生でも考えることができると思いますよ。

また，ホームページに僕でも解けるような問題が出たら，解かしていただきます。

＜水の流れ＞コメント:＜satoshi＞さん、本当にありがとうございます。次回には、第２回「算数・数学甲子園」という他のところで出された問題を考えています。対象者は小・中学生です。