�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����P�R�N�P�Q���R�O��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@�@�@�@��W�X�����w�I�ȉ������
�@�@�@�@�@�@�@�@�@�@����W���ԁF�P�Q���P�U���`�P�Q���R�P����
�m��̐ς̘a�n
�@�@�@
���A�����ɁA�����@���i���j���i�P�|���j�i�P�|�R���j�i�P�|�T���j�E�E�E�o�P�|�i�Q���\�P�j���j�@������B�����ŁA���ł��B
���P�F�@���́@�����@���i���j��W�J�����Ƃ��A���@�̌W�������߂�B
���Q�F�@���́@�����@���i���j��W�J�����Ƃ��A���Q�@�̌W�������߂�B
���R�F���̊�P�C�R�C�T�C�E�E�E�C�Q���\�P����d�������ɂ�����č�����ς��A���̑I�ѕ����ׂĂɂ킽���ĉ��������̂�
�@�@�@�@�@�o���@�Ƃ���Ƃ��A�o�P�{�o�Q�{�o�R�{�E�E�E�{�o�������߂�B
�m�n�P�u(^o^)BossF�v����̉@12��16���@�S��56����M�@�X�V12/30
���P�F
[��]�@�@-��(k=1�`��)k=-��2�@�c[��]
���Q�F [��]�@
��(k=1�`n)(2k-1)��(i=1�`k-1)(2i-1)
=��(k=1�`n)(2k-1)(k-1)2�@
=��(k=1�`n)(2k3-5k2+4k-1)
=�c=�i1/6�jn(n-1)(3��2-n-1)�c[��]�@�i���F�P�V���ɍŌ�̎����C���j
���R�F[��]
f(x)=1+��(k=1�`n)Pk(-x)k ������
��(k=1�`n)Pk=f(-1)-1=2x4x6x�c��(2n)-1=n!/2n-1�c[��]�@�i���F�ꕔ�C�����P�V���Ɏ�M�j
�m�n�Q�u�€�v����̉@12��18���@�S��17����M�@�X�V12/30
![]() �@��W�X�����
�@��W�X�����
���P
���̌W�����|���P�Ƃ����
![]()
![]() �i�Q��-1�j���|�Q
�i�Q��-1�j���|�Q![]()
�����@![]()
���@�Q
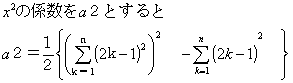
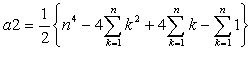

�m�n�R�O�ukashiwagi�v����̉@12��19���@8��12����M�@�X�V12/30
��P�D
��ӂ��@
���i���j���i�P−���j�i�P−�R���j�i�P−�T���j�E�E�E�o�P−�i�Q���\�P�j���p�@�\�\�\�@
���A���i���j����0�{��1���{���Q���Q�{�E�E�E�{��������
�\�\�\�A�ƒu��
�����ŁA���@�ƇA�̗��ӂ����Ŕ������A���ɂO��������B
���f�i���j���|�i�P−�R���j�i�P−�T���j�E�E�E�o�P−�i�Q���\�P�j���p
�@�@�@�@�@�@�|�R�i�P−���j�i�P−�T���j�E�E�E�o�P−�i�Q���\�P�j���p
�@�@�@�@�@�@�|�T�i�P−���j�i�P−�R���j�E�E�E�o�P−�i�Q���\�P�j���p
�@�@�@�@�@�@�@�E�E�E
�|�i�Q���\�P�j�i�P−���j�i�P−�R���j�E�E�E�o�P−�i�Q���\�R�j���p�\�\�\�B
���f�i���j����1�{�Q���Q���{�E�E�E�{�����������|�P�\�\�\�C
����ƇB�́|�P�|�R�|�T�\�\�\�\�\�\�@�|�i�Q���|�P�j�ƂȂ�B
����͊�Q���|�P�̂����P�`���܂ł̘a�Ƀ}�C�i�X���������̂ł��邩��|���Q
���A�A�͂�1�ƂȂ�B�Ƃ���ł��̌W���͂�1�ł��邩��A���߂���̂��|���Q�ƂȂ�B
��Q�D
��P�ƑS�����l�Ɏ��B�ƇC�̗��ӂ����Ŕ������A���ɂO��������B�����A�Q��������s���A�W�����r����ƁA���Q�͂��i���\�P�j�i�R���Q�\���\�P�j�^�U�ƂȂ�B
��R�D
���l�ɔ������J��Ԃ��A��P����Q�Ɠ��l�Ȍv�Z���s���ƁA�o�����i�|�P�j�������ƂȂ�B
�����A�|�Ɓ{���ЂƂ����ɂ������B�����A
�o�P�{�o�Q�{�o�R�{�E�E�E�{�o�����|��1�{���Q�|���R�{�E�E�E�{�i�|�P�j�������\�\�\�D
����͎��A�̂��Ɂ|�P�����������̂��炁0���P���������ł���B
�����Ň@�̂��ɂ��|�P��������ƁA
�Q�E�S�E�U�E�W�E�E�E�Q�����Q�����I
��������o�P�{�o�Q�{�o�R�{�E�E�E�{�o�����Q�����I�|�P�����߂���̂ł���B
<���̗���F�R�����g���@�ukashiwagi�v����̉�@�ɉs�����o�������܂����B���̂悤�ȍl�����A���I���n���g�E�I�C���[��1748�N�ɏo�ł����w������͏����x�̒��ɑ�����������@�ł��B���Ɋ��S���܂����B�@������āA���̃I�C���[���̘a�̋��ߕ����Љ�����ł��B
�ł́A�ꕔ�Љ�܂��B1�|���{��2�|���R�{���S�|���T�{�E�E�E���i�P�{���j�|�P�𗘗p���āA���̖����������s�v�c�Ȓl�ɂȂ�܂��B
��P�F1�|�P�{�P�|�P�{�P�|�P�{�E�E�E���P�^�Q
��Q�F�P�|�Q�P�{�R�P�|�S�P�{�T�P�|�U�P�{�E�E�E���P�^�S
��R�F�P�|�Q�Q�{�R�Q�|�S�Q�{�T�Q�|�U�Q�{�E�E�E���O
��S�F�P�|�Q�R�{�R�R�|�S�R�{�T�R�|�U�R�{�E�E�E���|�P�^�W
�m�n�R�P�ukashiwagi�v����̉@�����P�S�N1���S���@17��09����M�@�X�V1/14
�w�����܂��Ă��߂łƂ��������܂��B�{�N���ǂ�����낵�����w���̒����肢�\���グ�܂��B
���i���j���P�|���{���Q�|���R�{���S�|�@�|�|�|�|�@���P�^�i�P�{���j���������������Ηǂ��̂ł��ˁB
�@������Ǝv���Ă���Ă݂܂�����S��Ƃ������܂����B�������A�ŏ��͔����͂P�������A�����ƍl���Ă���܂����B�܂����R������Ƃ͎v���܂���ł����B
�@�P�`�R��̔��������ȉ��̗l�ɕ\���B�v�Z���������͖̂ʓ|�Ȃ̂ŏȗ������Ē����܂��B
�@���f�i���j���|�P�^�i�P�{���j�Q
�@���f�f�i���j���Q�^�i�P�{���j�R
�@���f�f�f�i���j���|�U�^�i�P�{���j�S
�����ォ�珇�ɇ@�A�A�A�B�y�чC�Ƃ���ƁA
��P�F���i�P�j���P�^�Q
��Q�F�|
���f�i�P�j���P�^�S
��R�F���f�i�P�j�{
���f�f�i�P�j���O
��S�F���f�i�P�j�{
���f�f�i�P�j�{���f�f�i�P�j�{ ���f�f�f�i�P�j
�@�@�@�@�����f�i�P�j�{�Q
���f�f�i�P�j�{ ���f�f�f�i�P�j
�@�@�@�@���|�P�^�W�@�@�ƂȂ�܂��B����Ȃ̂ł�낵���̂ł��傤���x
�����̗���F�R�����g���@���������H�v���āA�����������̂��ɂP��������ƁA�ȒP�ɏo�Ă��܂��B����ɁA���̕��@�ɂ͑���������܂��āA
��T�F�P�|�Q�S�{�R�S�|�S�S�{�T�S�|�U�S�{�E�E�E���O
��U�F�P�|�Q�T�{�R�T�|�S�T�{�T�T�|�U�T�{�E�E�E���P�^�S
��V�F�P�|�Q�U�{�R�U�|�S�U�{�T�U�|�U�U�{�E�E�E���O
��W�F�P�|�Q�V�{�R�V�|�S�V�{�T�V�|�U�V�{�E�E�E���|�P�V�^�P�U
��X�F�P�|�Q�W�{�R�W�|�S�W�{�T�W�|�U�W�{�E�E�E���O
��11�F�P�|�Q�X�{�R�X�|�S�X�{�T�X�|�U�X�{�E�E�E���R�P�^�S
�@���A�����̖��̏o�T�́A�u���n�ւ̐��w11�����v�ł��̂ŁA�����m���������B
�m�n�R�Q�ukashiwagi�v����̉@�����P�S�N1���X���@14��14����M�@�X�V1/14
�ukashiwagi�v�̃R�����g�F�w�X�əp���̑������̂��l���Ă���܂�����M���܂����B��肭����ό`���邱�Ƃ����l���Ă��炸�A���Ȃ莞�Ԃ��₵�܂������A�������Ƃ��ɂ͔��z�̓]���������Ώ�肭�s���̂ł��ˁB
��'(��)�{��''(��)�ɂ��������āA��������Ζ{���ɊȒP�ɂł��܂��ˁB�������A����Ȃ�p���������Ȃ��Ă����̋�J������܂���ˁB���������Ĕ����������ɍX�ɂ��������A��������Ηǂ��̂ł��ˁB
��́A���l�̑�����J��Ԃ������ł��ˁB���Ԃ͂�����܂������A�ʔ����A���̐[�������������Ē����܂����B�x
�m�n�R�R�ukashiwagi�v����̉@�����P�S�N1���P�O���@8��14����M�@�X�V1/14
�O�������ŁA��@�̊����ł̃��[�����܂����B
��(��)���P�^�i�P�{���j���P�|���{���Q�|���R�{���S�|�|�|�|�|
�|��'(��)���P�^�i�P�{���j�Q���P�P�|�Q���{�R���Q�|�S���R�{�T���S�|�|�|
��''(��)���Q�^�i�P�{���j�R
��'''(��)���|�@�U�^�i�P�{���j�S
���̎��ɂ��������āA
�|����'(��)�����^�i�P�{���j�Q���P�Q���|�Q���Q�{�R���R�|�S���S�{�T���T�|�|�|�|�|
���̎������Ŕ������āA
�|��'(��)�@�|����''(��)���P�Q�|�Q�Q���{�R�Q���Q�|�S�Q���R�{�T�Q���S�|�@�|�|�|�|�@�@�@
�����ł��ɂP��������ƁA
�|��'(�P)�@�|��''(�P)���P�^�S�|�P�^�S���O���P�Q�|�Q�Q�{�R�Q�|�S�Q�{�T�Q�|�@�|�|�|�|
��͂��̑�����J��Ԃ������A�����A�@�ɍēx���������A�������Ă��ɂP��������B
�����̗���F�R�����g���I�C���[���Ė{���ɑf���炵���p�m�̎�����ł��ˁB�����ƂƂ��ɁA�l�Ԃ̎��傫�Ȕ\�͂ɂ����Q���܂��B
�ukashiwagi�v����A�O�������ŁA��@�̊����łɎ���R�����g���܂����B
�w�������炸���ƃI�C���[�̓V�˂Ɛ��w�I���̐[�����[���Ɋy���܂��Ē����܂����B����Ȃɐ^���Ɉ�̎����l�����͉̂��\�N�Ԃ�ł��傤���B�w������̎������v���o���Ȃ���A�]�������o�����Ē����܂����B
�����ł̓��e��A�W��ƂX����v�Z���A�o���S�ăN���A�����Ē����܂����B�������A�p���������Ȃ�ƁA���X����ǂ��ł��ˁB����Ƃ��X�������肢�\���グ�܂��B�x
�m�n�S�u�l�c�v����̉@12��21���@10��38����M�@�X�V12/30
���P�F
�@�@��(��)��(�P�|��)(�P�|�R��)(�P�|�T��)�c�c�c{�P�|(�Q���|�P)��}
�@���̌W���́C
�@�@(�|�P)�E�P�E�P�E�c�c�c�E�P
�@�@�@�{�P�E(�|�R)�E�P�E�c�c�c�E�P
�@�@�@�{�P�E�P�E(�|�T)�E�P�E�c�c�c�E�P
�@�@�@�{�c�c�c
�@�@�@�{�P�E�P�E�P�E�c�c�c�E{�|(�Q���|�P)}
�@���|{�P�{�R�{�T�{�c�c�c�{(�Q���|�P)}
�@���|��(�����P�`��) (�Q���|�P)
�@���|{�Q�E��(���{�P)�^�Q�|��}
�@���|��^2
���Q�F
�@��^2�̌W���́C
�@�@(�|�P)(�|�R)�{(�|�P)(�|�T)�{(�|�P)(�|�V)�{�c�c�c�c�c�c�{(�|�P){�|(�Q���|�P)}
�@�@�@�{(�|�R)(�|�T)�{(�|�R)(�|�V)�{�c�c�c�c�c�c�{(�|�R){�|(�Q���|�P)}
�@�@�@�{�c�c�c�c�c�c
�@�@�@�{{�|(�Q���|�R)}{�|(�Q���|�P)}
�@��(�Q�E�P�|�P)��(�����Q�`��) (�Q���|�P)
�@�@�@�{(�Q�E�Q�|�P)��(�����R�`��) (�Q���|�P)
�@�@�@�{�c�c�c
�@�@�@�{{�Q(���|�P)�|�P}��(�j�����`��) (�Q���|�P)
�@����(m=1�`n-1) (�Q���|�P)��(k=m+1�`n) (�Q���|�P)
�@����(m=1�`n-1) (�Q���|�P){��(k=1�`n) (�Q���|�P)�|��(k���P�`m) (�Q���|�P)}
�@����(m=1�`n-1) (�Q���|�P)(��^2�|��^2)
�@����(m=1�`n-1) (�|�Q��^3�{��^2�{�Q����^2�|��^2)
�@���|�Q�E(���|�P)^2��^2�^�S�{(���|�P)��(�Q���|�P)�^�U�{�Q�E(���|�P)���^�Q�E��^2�|��^2(���|�P)
�@����(���|�P){�|�R��(���|�P)�{(�Q���|�P)�{�U��^2�|�U��}�^�U
�@����(���|�P)(�|�R��^2�{�R���{�Q���|�P�{�U��^2�|�U��)�^�U
�@����(���|�P)(�R��^2�|���|�P)�^�U
���R�F
�@���P�C�Q�Ɠ��l�ɂ�^r�̌W����(�|�P)^r�or�ƂȂ�D
�@�@(�P�|��)(�P�|�R��)(�P�|�T��)�c�c�c{�P�|(�Q���\�P)��}
�@���P�|�o1���{�o2��^2�{�c�c�c�{(�|�P)^n�on��^n
�ł��邩��C�����|�P�Ƃ���ƁC
�@�@(�P�{�P)(�P�{�R)(�P�{�T)�c�c�c{�P�{(�Q���\�P)}
�@���P�{�o1�{�o2�{�c�c�c�{�on
�@�@���o1�{�o2�{�o3�{�c�c�c�{�on
�@���Q�E�S�E�U�E�c�c�c�E�Q���|�P
�@���Q^n�i�P�E�Q�E�R�E�c�c�c�E��)�|�P
�@���Q^n�E���I�|�P
�@�@������@�@mizuryu@aqua.ocn.ne.jp
![]()
