平成14年6月16日
 [流れ星]
[流れ星]
第99回数学的な応募問題解答
<解答募集期間:6月1日〜6月15日>
[最長距離数]
太郎さんは、よく「図1のような碁盤の目になった町で、A地点からB地点への最短距離で行く道順の総数を求めよ。」と言う問題に出合います。これは組み合わせの考え方で解くことができます。
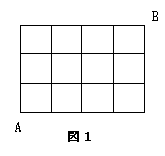
では、A地点からB地点へくねくねと遠回りをして行くと、最長距離数は幾つになるか。また、道順の総距離数は幾つになるかを考えました。ただし、同じ道を1回しか通れないものとし、小正方形の1辺の長さを1とする。
例えば、図2の1辺が2の正方形の場合は、総距離数Pは12,最短距離数Sは4、最長距離数Lは8になります。
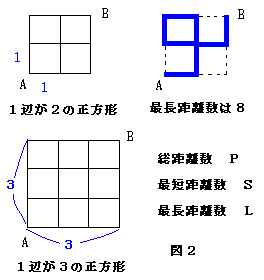
ここで、問題です。
問1.1辺が3の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問2.1辺が4の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問3.1辺が5の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問4.1辺がnの正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
次に、長方形の碁盤の目を考え、1辺の長さがmとnの長方形を考えます。
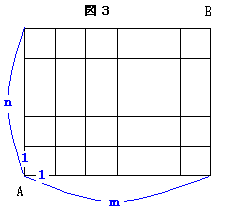
問5.(1)m、nがともに偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
(2)m、nがともに奇数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
(3)mが奇数、nが偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
<問題の出典は、数研出版が出している数研通信NO24の中にあったものです。>
NO1<H7K>さん 1回目の解答 6月2日 17:12受信 更新6月16日
今度の問題はかなり難しいですね。問1-4についてですが、
P=2n(n+1) S=2n は明らか。
しかし、Lが予想段階を抜けていません。L=2n^2となるような気がします。証明ができたらまた書きます。<以上の一報は6月1日の報告>
さっき横になって考えていましたら、「n*nの正方形のとき、L=2n^2」が示せました。
今から、それを書きます。メモとして書いているので、ちゃんとした説明は後日書きます。
A->Bの道は当然一筆なので、A,B以外の全ての点は偶点である。
端の4n点をA,B以外偶点にするには、そこの点から出ている線は常に二本でなければならない。
よって、L<=2n^2+2n-2n=2n^2(2n本の線をなくせば端についてA,B以外偶点にできる)
一方、2n^2での行き方は存在するので、L=2n^2.
<以上は6月1日の2回目報告>
1回目の解答 6月2日 17:12受信
問5関連で、ちょっと考えてみました。
n*mの長方形において、
P(n,m)=(n+1)m+(m+1)n=2mn+m+n
S(n,m)=m+n
は明らか。
さて、L(n,m)についてだがm>=nとしても一般性を失わない。(以下、L(n,m)をU(n,m)と表す。
U(1,m)=2*m(m;奇数)
U(1,m)=2*m+1(m;偶数)
であるが、また
U(n+1,m+1)>=U(n,m)+2+4*([(n+1)/2]+[(m+1)/2]-1) ((n奇数,m偶数)or(m奇数,n偶数))
=U(n,m)+2*(n+m)
>=U(n,m)+2+4*([(n+1)/2]+[(m+1)/2]) (n,m奇数)
=U(n,m)+2*(n+m+1)
>=U(n,m)+2+4*([(n+1)/2]+[(m+1)/2]-1) (n,m偶数)
=U(n,m)+2*(n+m+1)
が成立するので、
U(n,m) >=U(n-1,m-1)+2*(n+m-1) (n,m奇数 or n,m偶数)
=U(n-2,m-2)+2*(2n+2m-4)
=U(n-k,m-k)+2*(kn+km-k^2)
=U(1,m-n+1)+2*(n^2-n+mn-m-n^2+2n-1)
=U(1,m-n+1)+2*(mn-m+n-1)
=2mn
U(n,m) >=U(n-1,m-1)+2*(n+m-2) ((n奇数,m偶数)or(m奇数,n偶数))
=U(n-2,m-2)+2*(2n+2m-6)
=U(n-k,m-k)+2*(kn+km-k^2-k)
=U(1,m-n+1)+2*(n^2-n+mn-m-n^2+2n-1-n+1)
=U(1,m-n+1)+2*(mn-m)
=2*(m-n)+3+2*(mn-m)
=2mn-2n+3
である。
一方、一筆書きの話より
U(n,m)<=P(n,m)-(n-1)-(m-1)-2=2mn (n,m奇数 or n,m偶数)
U(n,m)<=P(n,m)-(n-1)-(m-1)-2=2mn (n,m奇数 or n,m偶数)
現在はここまでしか.. たぶんL(n,m)<=2mn-2n+2が示せると思うのですが...
<水の流れ:コメント> mが奇数、nが偶数のとき、L(n,m)の結果が私の解と異なっていますが・・・・
NO2<kashiwagi>さん 1回目の解答 6月3日 7:54受信 更新6月16日
第99回解答
問1〜4
題意に沿って一辺の長さが3や4の正方形で試みると、縦横とも3や4づつ通らない道がある場合に最長距離になることが分かる。総数や最短距離は自明であるので、以下の表に整理する。又、P=S+Lである。
|
一辺の長さ |
P |
S |
L |
|
3 |
24 |
6 |
18 |
|
4 |
40 |
8 |
32 |
|
5 |
60 |
10 |
50 |
|
n |
2n(n+1) |
2n |
2n^2 |
問5
長方形の場合も(m、n)=(3,1)、(4,2)の場合を試みると、上記と同様であることが分かる。但し、m、nが偶数と奇数が混じる場合は最長距離のみ異なる。以下の表に整理する。
|
CASE |
P |
S |
L |
|
m、nが偶数 |
2mn+m+n |
m+n |
2mn |
|
m、nが奇数 |
2mn+m+n |
m+n |
2mn |
|
mが奇数、nが偶数 |
2mn+m+n |
m+n |
2mn+m−n |
<水の流れ:コメント>mが奇数、nが偶数のとき、L=2mn+m−nに私の解と異なっていますが・・・・。
NO3<H7K>さん 2回目の解答 6月4日 19:19受信 更新6月16日
今までの解答をまとめてみました。
m*nの長方形での最少距離=S(m,n)、最長距離=L(m,n)、総距離数=P(m,n)とする。
P(m,n)=(m+1)n+(n+1)m=2mn+m+n、
S(m,n)=m+n
は明らか。
ここで、次の命題を示す。
「m≡n(mod 2)ならば、L(m,n)=2mn」「m-1≡n(mod 2)ならば、L(m,n)=2mn+1」
●L(1,n)>=2*n=2*1*n (n is odd)
L(1,n)>=2*n+1=2*1*n+1 (n is even)
であるので、m=1のときは両方とも成立。
●L(n+1,m+1)>=L(n,m)+2+4*([(n+1)/2]+[(m+1)/2]-1)=L(n,m)+2*(n+m) (m-1≡n(mod 2))
L(n+1,m+1)>=L(n,m)+2+4*([(n+1)/2]+[(m+1)/2])=L(n,m)+2*(n+m+1) (m≡n≡1(mod 2))
L(n+1,m+1)>=L(n,m)+2+4*([(n+1)/2]+[(m+1)/2]-1)=L(n,m)+2*(n+m+1) (m≡n≡0(mod 2))
が成立するので、m≡n(mod 2)のとき、「n=pの時成立すれば、n=p+1の時も成立。」
よって、m≡n(mod 2)のとき、L(n,m)>=2mn
●AからBへの道のりは一筆書きなので、縁に注目すると
m≡n(mod 2)のとき、L(n,m)<=P(n,m)-(n-1)-(m-1)-2=2mn
が成立。
よって、m≡n(mod 2)のとき、L(n,m)=2mn
一方、m-1≡n(mod 2)のとき、
●以下、m≡1としても一般性を失わない。
L(n+1,m+1)>=L(n,m+1)+1+4*[(m+1)/2]=2n(m+1)+2m+3=2nm+2n+2m+5=2(n+1)(m+1)+1
なので、m-1≡n(mod 2)のとき、L(n,m)>=2mn+1
●AからBへの道のりは一筆書きなので、縁に注目すると
m-1≡n(mod 2)のとき、L(n,m)<=P(n,m)-(n-1)-(m-1)-1=2mn+1
が成立。
よって、m-1≡n(mod 2)のとき、L(n,m)=2mn+1. //
以上より、
問1. P=24,S=6,L=18
問2. P=40,S=8,L=32
問3. P=60,S=10,L=50
問4. P=2(n^2+n),S=2n,L=2n^2
である。
<水の流れ:コメント> L(n,m)の値が同じになりました。
NO4<Iga>さん 解答 6月6日 18:19受信 更新6月16日
お久しぶりです、Igaです。またまたできそうだったのでやったらなんとかなりました。
よろしくお願いします。
総距離数P
まず、 縦の道(|)の合計=縦の長さ×本数
=縦の長さ×{横の道(−)の数+1}
同様に、横の道(−)の合計=横の長さ×本数
=横の長さ×{縦の道(|)の数+1}
よって、総距離数P=縦の長さ×{横の道の数+1}+横の長さ×{縦の道の数+1}
正方形の場合、縦の長さと横の長さは同じだから、1辺の長さをnとすると
総距離数P=n×(n+1)×2
最短距離数S
経路は他にも考えられるが、一番外枠の道を選んだ場合が最短になることは明らか。
よって、最短距離数S=縦の長さ+横の長さ
正方形の場合、縦の長さと横の長さは同じだから、1辺の長さをnとすると、
最短距離数S=n×2
最長距離数L
これは実際に図をかいて、数えてみました。
n P S L
2 12 4 8
3 24 6 18
4 40 8 32
ここまでやってみて、L=P−S という関係があることに気づいたので、
5 60 10 50
nのときはP=2n(n+1)、S=2nを代入して、
L=P−S
=2n(n+1)−2n
=2n^2
以上のようになりました。
次に、長方形の碁盤の目を考え、1辺の長さがmとnの長方形を考えます。
問5
(1)m、nがともに偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
m=2,n=4のときを例にして数えてみました。
総距離数P=22 、最短距離数S=6はすぐに求められました。
最長距離数Lは図をかいて求めたら、16となりました。
よって、正方形のときと同じように考えて、
P=n(m+1)+m(n+1) 、S=m+n
であるから、最長距離数Lは、
L=P−S
=n(m+1)+m(n+1)−(m+n)
=2mn
(2)m、nがともに奇数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
m=3,n=5のときを例にして数えてみました。
総距離数P=38 、最短距離数S=8はすぐに求められました。
最長距離数Lは図をかいて求めたら、30となりました。
よって、(1)と同様に、
L=2mn
(3)mが奇数、nが偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
m=3,n=2のときを例にして数えてみました。
総距離数P=17 、最短距離数S=5はすぐに求められました。
最長距離数Lは図をかいて求めたら、13となりました。
今までと同じ関係があるなら、L=17−5で、12となるはずなので数え間違いかと思い、何度も確認しましたが、最長距離数は13でした。
何が違うのかいろいろと考えているうちに、同じ道を通らないということから、一筆書きを思いつきました。一筆書きができるかどうかを判断するのに、奇数本の線の集まる奇点の個数をかぞえるというやつです。
●−○−○−G 左の図で、Sはスタートで、Gはゴール、
| | | | ●は偶点、 ○は奇点を表しています。
○−●−●−○D
| | | |
○−●−●−○C
| | | |
S −○−○−●
A B
SとGはその性質上、奇点扱いになります。(Sからは2本の道がありますが、
Sから横へいったら、Sから縦につながっている道を通ることはできません。Gも同様)
ここで、最長距離数となるには、通らない道をできるだけ減らす必要があります。
奇点につながっている道のうちの一つは、通らない道となるので、そのままでは単純に奇点の数だけ通らない道ができてしまいます。通らない道を減らすためには、隣り合った奇点と奇点の間の道を通らない道とすることにより、半減します。(上の図のAB間、CD間)
しかし、この図のような奇点の配置だと、10個の奇点のうちAB間のような組み合わせは4組しか作ることができず、2個の奇点は孤立してしまいます。
そのため通らない道の数は、この図の場合で10−4=6本ということになります。
1辺長さがnの正方形の場合、奇点の数は(n−1)×4個、孤立する2個を仮にSとGとすれば、
半減できる道の数は((n−1)×4)÷2となるので、通らない道の数は
(n−1)×4−(n−1)×2+2=2n となります。
この数が最短距離数Sと一致するので、問い5(3)以外はL=P−Sという関係が成り立ちます。
●−○−○−G
| | | |
○−●−●−○
| | | |
S −○−○−●
mが奇数、nが偶数のときは、その他の場合にあったように奇点を孤立させることなく、
隣り合った奇点の組を作ることができます。
その結果、奇点の数は (m−1)×2+(n−1)×2個、
SとGの2個を加えて、奇点の2個組の数は m+n+1組、
したがって通らない道の数も(m+n+1)本となり、総距離数Lから引くと最長距離数L
が求められます。
L=P−(m+n+1)
=n(m+1)+m(n+1)−(m+n+1)
=2mn+1
以上です。何とか自分なりに納得行く解答が出せたので満足しています。
またよろしくお願いします。
<水の流れ:コメント> 当初、m、nが奇数であろうが偶数であろうが、P=S+Lが成り立つと考えていましたが、この解答で自分の間違いに気がつきました。これまで、ご迷惑をおかけしたことの お詫びします。
で、mが奇数、nが偶数のときは、P=S+L―1になっていました。
NO5<kashiwagi>さん2回目の解答 6月10日 7:46受信 更新6月16日
問5の(3)のS,Lが違うとの事でしたが、Lは理論式の導出で計算ミスをしておりました。
長方形の場合も(m、n)=(3,1)、(4,2)の場合を試みると、上記と同様であることが分かる。但し、m、nが偶数と奇数が混じる場合は最長距離のみ異なる。以下の表に整理する。
|
CASE |
P |
S |
L |
|
m、nが偶数 |
2mn+m+n |
m+n |
2mn |
|
m、nが奇数 |
2mn+m+n |
m+n |
2mn |
|
mが奇数、nが偶数 |
2mn+m+n |
m+n |
2mn+1 |
関係式はm、nのどちらも偶数か奇数の時はP=S+L
m、nの片方が偶数、もう一方が奇数の時はP=S+L−1
<水の流れ:コメント> 当初、m、nが奇数であろうが偶数であろうが、P=S+Lが成り立つと考えていましたが、この解答で自分の間違いに気がつきました。これまで、ご迷惑をおかけしたことの お詫びします。
で、mが奇数、nが偶数のときは、P=S+L―1になっていました。
![]()
