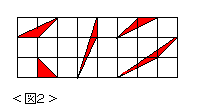
丂丂丂丂丂師偵丄恾俁偺傛偆偵嵗昗暯柺忋偱丄揰俙乮倫丆倯乯偲庢傝丄慄暘俷俙傪惓偺岦偒偵
丂丂丂丂夞揮偟偰丆慄暘俷俛偵側傞傛偆偵丄揰俛乮倰丆倱乯傪庢傞丅
| 栤戣 嶰曈偺挿偝偑併俀俋丄併俀俇丄俁併俆 偱偁傞嶰妏宍偺柺愊傪媮傔傛丅 |
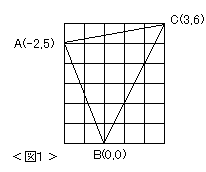
| 乽俹倝們倠偺掕棟乿丗暯柺忋偺奿巕懡妏宍俵偵偍偄偰丄曈忋偵偁傞奿巕揰偺屄悢傪倐 俵偺撪晹偵偁傞奿巕揰偺悢傪們偲偡傞偲丄偦偺柺愊俽(俵) 偼師偺幃偱昞偝傟傞丅 俽(俵)亖乮們亅侾乯亄倐乛俀 |
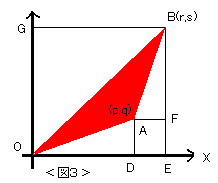
| 柦戣侾丗乮捀揰偺傒偑奿巕揰偱偁傞嶰妏宍偺応崌乯 撪晹偵傕曈忋偵傕奿巕揰偑側偔丄捀揰偺傒偑奿巕揰偱偁傞嶰妏宍仯乮埲壓婎杮 嶰妏宍偲屇傇乯偺柺愊偼侾乛俀偱偁傞丅 偡側傢偪丄俽(仯)亖侾乛俀丒丒丒嘆 |

丂丂丂丂丂師偵丄恾俁偺傛偆偵嵗昗暯柺忋偱丄揰俙乮倫丆倯乯偲庢傝丄慄暘俷俙傪惓偺岦偒偵
丂丂丂丂夞揮偟偰丆慄暘俷俛偵側傞傛偆偵丄揰俛乮倰丆倱乯傪庢傞丅
| 柦戣俀丗奿巕懡妏宍偼婎杮嶰妏宍偵暘妱偱偒傞丅 |
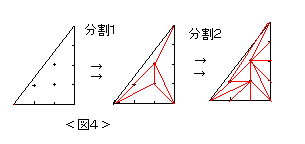
| 柦戣俁丗奿巕懡妏宍俵傪婎杮嶰妏宍偵暘妱偟偨偲偒丄 嶰妏宍偺悢偼俀們亄倐亅俀 偱偁傞丅 偨偩偟丄們偼俵偺撪晹偵偁傞奿巕揰偺悢丄倐偼曈忋偵偁傞奿巕揰偺悢偱偁傞丅 |
亙姶憐丗偙傫側偵丄慺惏傜偟偔旤偟偄掕棟傪戝妛擖帋偵巊偭偰傕傛偄偺偐側乕丅亜