平成２７年３月８日

[流れ星]

　　　　　第31７回数学的な応募解答

　　　　　　＜解答募集期間：２月８日〜３月８日＞

［垂足三角形の面積］

垂足三角形というのは、三角形において頂点から対辺に下ろした３つの垂線の足を結ぶ三角形のことです。しかし、ここでは意味を広げ、任意の一点Ｐからの三角形の3辺またはその延長上に下ろした垂線を結び三角形をＰの垂足三角形とよぶことにし、その面積をＳ（Ｐ）で表すことにする。
　今後、三角形ＡＢＣにおいて、一点Ｐから３辺ＢＣ，ＣＡ，ＡＢに下ろした垂線の足をそれぞれＬ，Ｍ，Ｎで表す。また、三角形ＡＢＣの面積をＳ、外心をＯ、内心をＩ、さらに、外接円の半径をＲ、内接円の半径をｒとする。

問題１：点Ｐが外心Ｏのとき、垂足三角形の面積Ｓ（Ｏ）をＳで表せ。

問題２：点Ｐが内心Ｉのとき、垂足三角形の面積Ｓ（Ｉ）をＳ、Ｒ，ｒで表せ。

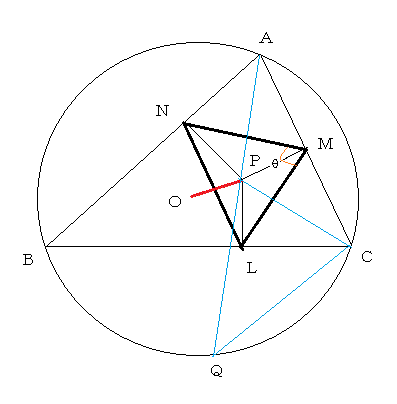問題３：任意の点Ｐの垂足三角形の面積Ｓ（Ｐ）は、点Ｐの位置によって変わる。ここで、点Ｐと外心Ｏとの距離をｄとすれば、
等式　Ｓ（Ｐ）＝（１／４Ｒ^２）Ｓ（Ｒ^２−ｄ^２）　が成り立つことを次の順に示せ。

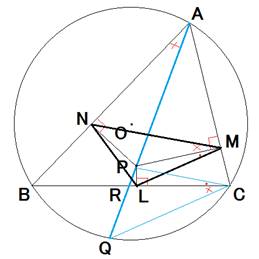
（１）∠ＬＭＮ＝θとおくと、Ｓ（Ｐ）＝（１／２）ＡＰ・ＣＰsinθsinＡsinＣ

（２）直線ＡＰと外接円との交点をＱとし、ＣとＰ、ＣとＱを結んで三角形ＣＰＱにおいて、
Ｓ（Ｐ）＝（１／２）ＡＰ・ＰＱsinＡsinＢsinＣ

（３）Ｓ（Ｐ）＝（１／４Ｒ^２）Ｓ（Ｒ^２−ｄ^２）

注意：任意の点Pですが、図のように三角形ＡＢＣの内部にあるときのＰとして考えてください。

問題４：三角形ＡＢＣの外接円上の点Ｐから３辺に下ろした垂線の足は一直線上にあることを示せ。また、この逆も成り立つ。＜シムソン線の定理＞

問題５：次の等式　ＯＩ^２＝Ｒ^２−２Ｒｒを示せ。＜オイラーの定理（平面幾何学＞＞

＜参考文献：数学ひとり旅　数学＝不思議発見　石谷　茂（現代数学社）＞

ＮＯ１「uchinyan」 02/08 15時08分　受信 更新 3/8

問題１：

P = O のとき，

L，M，N は BC，CA，AB の中点になるので，△LMN と △ABC は相似で相似比は 1：2，なので，

S(O) = S/4

問題２：

P = I のとき，

IL = IM = IN = r，∠MIN = 180°- A，∠NIL = 180°- B，∠LIM = 180°- C，なので，

S(I) = r^2/2 * (sin(∠MIN) + sin(∠NIL) + sin(∠LIM)) = r^2/2 * (sinA + sinB + sinC)

正弦定理より，

= r^2/2 * (BC + CA + AB)/(2R) = r(BC + CA + AB)/2 * r/(2R) = Sr/(2R)

問題３：

(1)

S(P) = 1/2 * ML * MN * sinθ

ここで，∠PLC = ∠PMC = 90°なので P，L，C，M は同一円周上にあり，トレミーの定理より，

ML * CP = PM * CL + PL * CM

= CPsin(∠PCM) * CPcos(∠PCL) + CPsin(∠PCL) * CPcos(∠PCM) = CP^2 * sin(∠PCM + ∠PCL) = CP^2 * sinC

ML = CPsinC

同様にして，∠PMA = ∠PNA = 90°より P，M，A，N は同一円周上にあり，トレミーの定理を使って，

MN = APsinA がいえます。そこで，

S(P) = (1/2)(AP * CP)sinθsinAsinC

(2)

△PQC に注目すると，

∠PQC = ∠AQC = ∠ABC = B

∠PCQ = ∠PCB + ∠BCQ = ∠PCM + ∠BAQ = ∠PCM + ∠NAP

P，L，C，M は同一円周上にあったので，∠PCL = ∠PML，

P，M，A，N は同一円周上にあったので，∠NAP = ∠NMP，となって，

∠PCQ = ∠PCM + ∠NAP = ∠PML + ∠NMP = ∠LMN = θ，がいえ，

CPsinθ = PQsinB，になります。そこで，

S(P) = (1/2)(AP * PQ)sinAsinBsinC

(3)

O，P を通る直線を引き 円O との交点を D，E とすると，方べきの定理より，

AP * PQ = DP * EP = (R + d)(R - d) = R^2 - d^2

また，正弦定理も使って，

S(P) = (1/2)(AP * PQ)sinAsinBsinC

= (1/2)(R^2 - d^2)(AB/(2R) * AC/(2R))sinA = (1/(4R^2))(1/2 * AB * AC * sinA)(R^2 - d^2)

S(P) = (1/(4R^2))S(R^2 - d^2)

になります。

問題４：

P が △ABC の外接円上にある場合，例えば，問題３：の図で P -> Q の場合，で問題３：を再考してみます。

P ≠ Q ならば，角度の引き算や補角を考えるなどの差異はありますが，

(1)も(2)も(3)も，同様にして成立することが分かります。

P -> Q としても状況は連続的にしか変化しないので，P = Q になっても，

S(P) = (1/(4R^2))S(R^2 - d^2)，は成立します。

そこで，この式で P が △ABC の外接円上にある場合というのは d = PO = R なので，

S(P) = (1/(4R^2))S(R^2 - R^2) = 0

これは △LMN がつぶれて，垂線の足 L，M，N が同一直線上にあることを示しています。

逆に，垂線の足 L，M，N が同一直線上にあれば △LMN がつぶれて，

S(P) = (1/(4R^2))S(R^2 - d^2) = 0，d = PO = R

つまり，P が △ABC の外接円上にあります。

問題５：

問題３：と問題２：の結果を使うと，

S(P) = (1/(4R^2))S(R^2 - d^2) = Sr/(2R)，R^2 - d^2 = 2Rr，

OI^2 = R^2 - 2Rr

がいえます。

(感想)

これは面白い問題でした。特に，シムソン線の定理，オイラーの定理はいずれも以前に証明したことがありますが，

苦労した覚えがあります。

ところが，この方法だと特殊な場合としてまとめて証明できてしまうのがすごいです。

もっとも，ポイントの問題３：は誘導があったのでよかったのですが，誘導なしではかなりの難問のような気もします。うる覚えですが，オイラーの定理の証明も似たような感じでできた記憶があります。なお，面倒なので省略しますが，確かに一般の P に対して，

S(P) = (1/(4R^2))S(R^2 - d^2)

が成立するようです。

ただし，P が外接円の外部にあるときは角度の取り方によるわけですが，S(P) が負になりますね。

ＮＯ２「早起きのおじさん」 02/12 10時37分　受信 更新 3/8

問題1

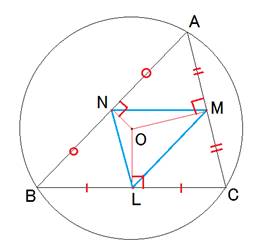・点が三角形ABCの外心Oであれば、

3辺への垂線の足L、M、Nは各辺の中点です。

・各中点を結べば、各辺と平行になります。

・□ANLM、□BLMN、□CMNLは平行四辺形です。

・平行四辺形は対角線で2等分されます。

よって、

問題2

・三角形ABCの内心Iから3辺への垂線の足を

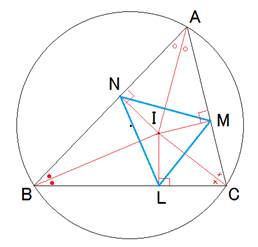L、M、Nとします。

・IL＝IM＝IN＝rです。

・□ANIM、□BLIN、□CMILが円に内接するので、

∠MIN＝π−∠A、∠NIL＝π−∠B、∠LIM=π−∠Cです。

・正弦定理より、

よって、

問題3

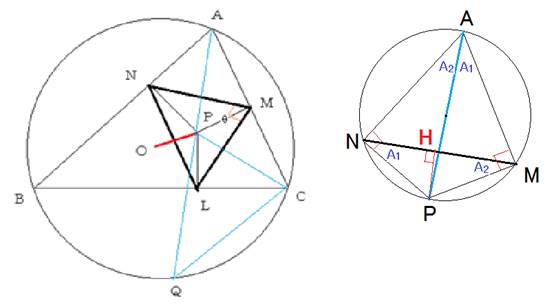
(1)

・左の図で、□ANPMは円に内接します。

・APは、∠Aを2つの角にわけます。

・円周角の定理により、∠PAM＝∠PNM、∠PAN＝∠PMNです。

・PからMNへの垂線の足をHとすると、

MN＝MH＋HN＝PMcosA₂＋PNcosA₁

＝APsinA₁･cosA₂＋APsinA₂･cosA₁

＝AP(sinA₁･cosA₂＋cosA₁･sinA₂)

＝AP･sin (A₁＋A₂)＝AP･sin A

・同様に、LM＝CP･sin Cになります。

よって、

(2)AQとBCの交点をRとします。

・問題3 (1)にあるように、∠PMN＝∠PABです。

・△ABR∽△CQRなので、∠RAB＝RCQです。

よって、∠PMN＝RCQです。･･･(ｱ)

・□CMPLが円に内接するので∠PML＝PCLです。･･･(ｲ)

(ｱ)、(ｲ)より、∠LMN＝∠PCQ(＝θ)です。

・∠B＝∠Qなので、△CQPに正弦定理をあてはめると、

以上から、(1)の結果を変形すると、

(3)直線OPと円との交点を図のように、S、Tとおきます。

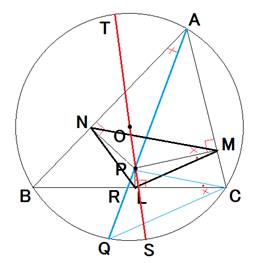・方べきの定理より、AP･PQ＝TP･PS＝(R＋d)(R−d)＝R²−d²

以上をふまえて、(2)の結果より、

問題4

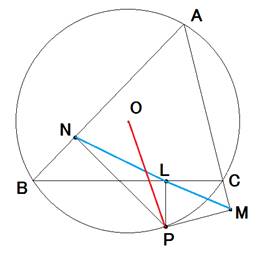・点Pが円周上にあれば、d＝OP＝Rです。

・問題3 (3)の結果に代入すると、

面積が0ということは、△LMNがつぶれているということなので、

3点M、L、Nは、同一直線上にあります。

問題5

この2式から、

感想：今回の問題は解いていてとても楽しかったです。毎日少しずつ解いてわくわくしました。全部解けたときはもう終わりかと残念な感じがしました。

ＮＯ３「浜田明巳」 02/23 13時33分　受信 更新 3/8

問題１
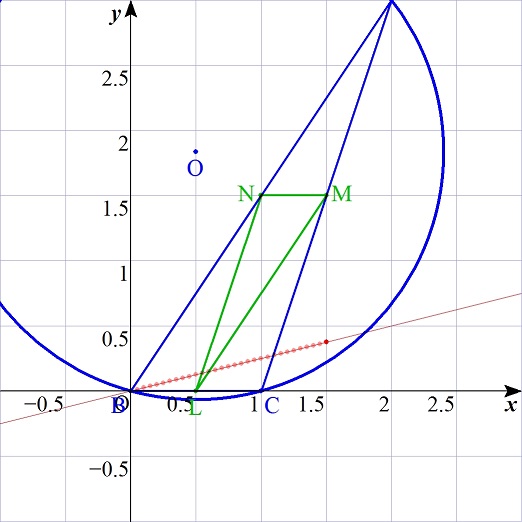
　ＧＲＡＰＥＳで計算する．
　Ｂ(０，０)，Ｃ(１，０)とし，点Ａ(Ａｘ，Ａｙ)を，−１≦Ａｘ≦２，０＜Ａｙ≦３の範囲でシラミつぶしに決める．
　その都度，外心Ｏを求め，垂線の足Ｌ，Ｍ，Ｎを求める．
　Ｓ＝△ＡＢＣ，Ｓ(Ｏ)＝△ＬＭＮを計算し，点(Ｓ，Ｓ(Ｏ))を図示する．
　この点が直線ｙ＝１／４・ｘ上にあるので，答は，
　　Ｓ(Ｏ)＝１／４・Ｓ
である．

//Clickで計算開始
clraimg
P.x:=100
P.y:=100
clraimg
draw
k:=.1
for A.x:=-1 to 2 step k
  for A.y:=k to 3 step k
      P.x:=.5*C.x*A.y
      P.y:=.5*abs((M.x-L.x)*(N.y-L.y)-(N.x-L.x)*(M.y-L.y))
      draw
  next A.y
next A.x


問題２
　問題１と同様に，ＧＲＡＰＥＳで計算する．
　外心Ｏ，内心Iを求め，内心からの垂線の足Ｌ，Ｍ，Ｎを求める．
　Ｓ＝△ＡＢＣ，Ｓ(Ｉ)＝△ＬＭＮ，Ｒ，ｒを計算し，点((Ｓ・ｒ)／Ｒ，Ｓ(Ｉ))を図示する．
　この点が直線ｙ＝１／２・ｘ上にあるので，答は，
　　Ｓ(Ｉ)＝１／２・(Ｓ・ｒ)／Ｒ＝(Ｓ・ｒ)／(２・Ｒ)
である．

//Clickで計算開始
clraimg
P.x:=100
P.y:=100
clraimg
draw
k:=.1
for A.x:=-1 to 2 step k
  for A.y:=k to 3 step k
      P.x:=(.5*C.x*A.y)*I.r/D.r
      P.y:=.5*abs((M.x-L.x)*(N.y-L.y)-(N.x-L.x)*(M.y-L.y))
      draw
  next A.y
next A.x


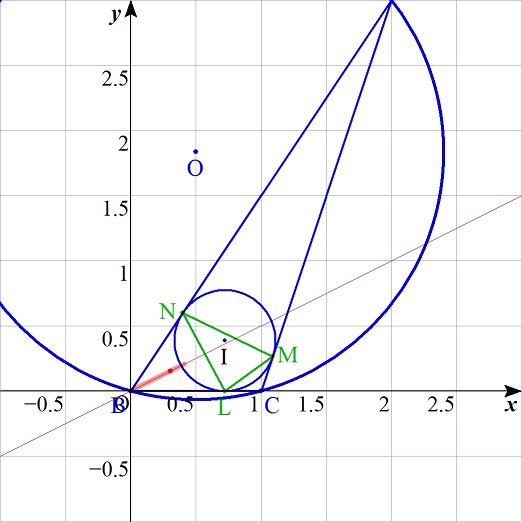
問題３
　ＶＢＳＣＲＩＰＴで計算する．
　座標系を導入する．Ｂ(０，０)，Ｃ(１，０)とし，点Ａ(Ａｘ，Ａｙ)を，０≦Ａｘ＜１，０.２≦Ａｙ＜１.２の範囲でランダムに決める．
　点Ｐを△ＡＢＣの内部にシラミつぶしに決めていき，その都度，差
　（１）Ｓ(Ｐ)−１／２・ＡＰ・ＣＰ・sinθ・sinＡ・sinＣ
　（２）Ｓ(Ｐ)−１／２・ＡＰ・ＰＱ・sinＡ・sinＢ・sinＣ
　（３）Ｓ(Ｐ)−１／(４Ｒ^２)・Ｓ・(Ｒ^２−ｄ^２)
を計算し，それぞれの平均，分散を求める．
　平均，分散がほぼ０に近い値となれば，情報数学的に証明される．

randomize:Ax=rnd(1):Ay=rnd(1)+.2
BC=1:Bx=0:By=0:Cx=BC:Cy=0:Ly=0:Ox=.5*(Bx+Cx)
S=.5*BC*(Ay-By)
'ABの垂直二等分線:y=-(Bx-Ax)/(By-Ay)*(x-.5*(Ax+Bx))+.5*(Ay+By)=a*x+b
a=-(Bx-Ax)/(By-Ay):b=a*(-.5*(Ax+Bx))+.5*(Ay+By)
Oy=a*Ox+b
R=sqr((Ox-Ax)*(Ox-Ax)+(Oy-Ay)*(Oy-Ay))
AB=sqr((Bx-Ax)*(Bx-Ax)+(By-Ay)*(By-Ay))
AC=sqr((Cx-Ax)*(Cx-Ax)+(Cy-Ay)*(Cy-Ay))
sinA=BC/(2*R):sinB=AC/(2*R):sinC=AB/(2*R)
kizami=.01
n=0:k11=0:k12=0:k21=0:k22=0:k31=0:k32=0
for Px=Bx to Cx step kizami
  Lx=Px
  if Ax>=Px then
    Pymax=(By-Ay)/(Bx-Ax)*(Px-Ax)+Ay
  else
    Pymax=(Cy-Ay)/(Cx-Ax)*(Px-Ax)+Ay
  end if
  for Py=kizami to Pymax step kizami
    if (By-Ay)/(Bx-Ax)*(Px-Ax)+Ay>Py and (Cy-Ay)/(Cx-Ax)*(Px-Ax)+Ay>Py then
      AP=sqr((Px-Ax)*(Px-Ax)+(Py-Ay)*(Py-Ay))
      CP=sqr((Px-Cx)*(Px-Cx)+(Py-Cy)*(Py-Cy))
      'AC:y=(Cy-Ay)/(Cx-Ax)*(x-Ax)+Ay=a*x+b
      a=(Cy-Ay)/(Cx-Ax):b=a*(-Ax)+Ay
      'PからACに下ろした垂線:y=-(Cx-Ax)/(Cy-Ay)*(x-Px)+Py=c*x+d
      c=-(Cx-Ax)/(Cy-Ay):d=c*(-Px)+Py
      'My=a*Mx+b=c*Mx+d
      Mx=(d-b)/(a-c):My=a*Mx+b
      'AB:y=(By-Ay)/(Bx-Ax)*(x-Ax)+Ay=a*x+b
      a=(By-Ay)/(Bx-Ax):b=a*(-Ax)+Ay
      'PからABに下ろした垂線:y=-(Bx-Ax)/(By-Ay)*(x-Px)+Py=c*x+d
      c=-(Bx-Ax)/(By-Ay):d=c*(-Px)+Py
      'Ny=a*Nx+b=c*Nx+d
      Nx=(d-b)/(a-c):Ny=a*Nx+b
      SP=.5*abs((Mx-Lx)*(Ny-Ly)-(Nx-Lx)*(My-Ly))
      LM2=(Mx-Lx)*(Mx-Lx)+(My-Ly)*(My-Ly)
      MN2=(Nx-Mx)*(Nx-Mx)+(Ny-My)*(Ny-My)
      NL2=(Lx-Nx)*(Lx-Nx)+(Ly-Ny)*(Ly-Ny)
      cost=(LM2+MN2-NL2)/(2*sqr(LM2)*sqr(MN2)):sint=sqr(1-cost*cost)
      sa=SP-.5*AP*CP*sint*sinA*sinC
      k11=k11+sa:k12=k12+sa*sa
      '
      'AP:y=(Py-Ay)/(Px-Ax)*(x-Ax)+Ay=a*x+b
      a=(Py-Ay)/(Px-Ax):b=a*(-Ax)+Ay
      '円O:(x-Ox)^2+(y-Oy)^2=R^2->(x-Ox)^2+((a*x+b)-Oy)^2=R^2->aa*x^2+2*bb*x+cc=0
      aa=1+a*a:bb=-Ox+a*(b-Oy):cc=Ox*Ox+(b-Oy)*(b-Oy)-R*R
      Q1x=(-bb+sqr(bb*bb-aa*cc))/aa:Q1y=a*Q1x+b
      AQ1=sqr((Q1x-Ax)*(Q1x-Ax)+(Q1y-Ay)*(Q1y-Ay))
      Q2x=(-bb-sqr(bb*bb-aa*cc))/aa:Q2y=a*Q2x+b
      AQ2=sqr((Q2x-Ax)*(Q2x-Ax)+(Q2y-Ay)*(Q2y-Ay))
      if AQ1>AQ2 then
        Qx=Q1x:Qy=Q1y
      else
        Qx=Q2x:Qy=Q2y
      end if
      PQ=sqr((Qx-Px)*(Qx-Px)+(Qy-Py)*(Qy-Py))
      sa=SP-.5*AP*PQ*sinA*sinB*sinC
      k21=k21+sa:k22=k22+sa*sa
      '
      OP2=(Px-Ox)*(Px-Ox)+(Py-Oy)*(Py-Oy)
      sa=SP-1/(4*R*R)*S*(R*R-OP2)
      k31=k31+sa:k32=k32+sa*sa:n=n+1
    end if
  next
next
kotae="問題3.(1)平均="&(k11/n)
kotae=kotae&chr(13)&"問題3.(1)分散="&(k12/n-(k11/n)*(k11/n))
kotae=kotae&chr(13)&"問題3.(2)平均="&(k21/n)
kotae=kotae&chr(13)&"問題3.(2)分散="&(k22/n-(k21/n)*(k21/n))
kotae=kotae&chr(13)&"問題3.(3)平均="&(k31/n)
kotae=kotae&chr(13)&"問題3.(3)分散="&(k32/n-(k31/n)*(k31/n))
msgbox kotae

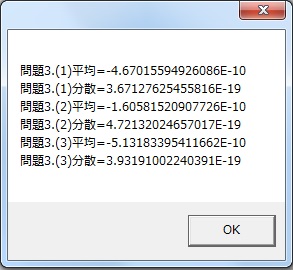
　故に証明された．

問題４
　問題３と同様に計算する．
　点Ｐを△ＡＢＣの外接円上にシラミつぶしに決めていき，その都度，
　　∠ＬＭＮ＝０または∠ＬＭＮ＝π
であることを示す為に，
　　(cos∠ＬＭＮ−１)・(cos∠ＬＭＮ−(−１))
を計算し，その平均，分散を求める．
　平均，分散がほぼ０に近い値となれば，情報数学的に証明される．

randomize:Ax=rnd(1):Ay=rnd(1)+.2
BC=1:Bx=0:By=0:Cx=BC:Cy=0:Ly=0:Ox=.5*(Bx+Cx)
'ABの垂直二等分線:y=-(Bx-Ax)/(By-Ay)*(x-.5*(Ax+Bx))+.5*(Ay+By)=a*x+b
a=-(Bx-Ax)/(By-Ay):b=a*(-.5*(Ax+Bx))+.5*(Ay+By)
Oy=a*Ox+b
R=sqr((Ox-Ax)*(Ox-Ax)+(Oy-Ay)*(Oy-Ay))
kizami=.01
n=0:k1=0:k2=0:pi=4*atn(1)
for t=0 to 2*pi step kizami
  Px=Ox+R*cos(t):Py=Oy+R*sin(t):Lx=Px
  'AC:y=(Cy-Ay)/(Cx-Ax)*(x-Ax)+Ay=a*x+b
  a=(Cy-Ay)/(Cx-Ax):b=a*(-Ax)+Ay
  'PからACに下ろした垂線:y=-(Cx-Ax)/(Cy-Ay)*(x-Px)+Py=c*x+d
  c=-(Cx-Ax)/(Cy-Ay):d=c*(-Px)+Py
  'My=a*Mx+b=c*Mx+d
  Mx=(d-b)/(a-c):My=a*Mx+b
  'AB:y=(By-Ay)/(Bx-Ax)*(x-Ax)+Ay=a*x+b
  a=(By-Ay)/(Bx-Ax):b=a*(-Ax)+Ay
  'PからABに下ろした垂線:y=-(Bx-Ax)/(By-Ay)*(x-Px)+Py=c*x+d
  c=-(Bx-Ax)/(By-Ay):d=c*(-Px)+Py
  'Ny=a*Nx+b=c*Nx+d
  Nx=(d-b)/(a-c):Ny=a*Nx+b
  LM2=(Mx-Lx)*(Mx-Lx)+(My-Ly)*(My-Ly)
  MN2=(Nx-Mx)*(Nx-Mx)+(Ny-My)*(Ny-My)
  NL2=(Lx-Nx)*(Lx-Nx)+(Ly-Ny)*(Ly-Ny)
  cost=(LM2+MN2-NL2)/(2*sqr(LM2)*sqr(MN2))
  s=(cost-1)*(cost-(-1))
  k1=k1+s:k2=k2+s*s:n=n+1
next
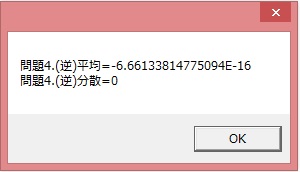
kotae="問題4.平均="&(k1/n)
kotae=kotae&chr(13)&"問題4.分散="&(k2/n-(k1/n)*(k1/n))
msgbox kotae

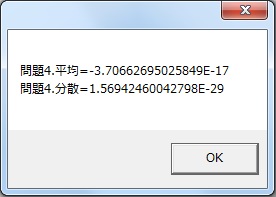
　故に証明された．

問題５
　問題３，４と同様に計算する．
　Ｂ(０，０)，Ｃ(１，０)とし，点Ａ(Ａｘ，Ａｙ)を，−１≦Ａｘ＜２，０.２≦Ａｙ＜２の範囲でシラミつぶしに決める．
　その都度，外心Ｏ，外接円の半径Ｒ，内心Ｉ，内接円の半径ｒ，ｄ＝ＯＩを求め，差
　　ＯＩ^２−(Ｒ^２−２・Ｒ・ｒ)
を計算し，その平均，分散を求める．
　平均，分散がほぼ０に近い値となれば，情報数学的に証明される．

BC=1:Bx=0:By=0:Cx=BC:Cy=0:Ly=0:Ox=.5*(Bx+Cx)
kizami=.01:n=0
for Ax=-Cx to Cx*2 step kizami
  for Ay=.2 to BC*2 step kizami
    'ABの垂直二等分線:y=-(Bx-Ax)/(By-Ay)*(x-.5*(Ax+Bx))+.5*(Ay+By)=a*x+b
    a=-(Bx-Ax)/(By-Ay):b=a*(-.5*(Ax+Bx))+.5*(Ay+By)
    Oy=a*Ox+b
    R=sqr((Ox-Ax)*(Ox-Ax)+(Oy-Ay)*(Oy-Ay))
    AB=sqr((Bx-Ax)*(Bx-Ax)+(By-Ay)*(By-Ay))
    AC=sqr((Cx-Ax)*(Cx-Ax)+(Cy-Ay)*(Cy-Ay))
    'D:∠BACの二等分線とBCとの交点
    Dx=(AC*Bx+AB*Cx)/(AB+AC):Dy=(AC*By+AB*Cy)/(AB+AC)
    'E:∠ABCの二等分線とACとの交点
    Ex=(BC*Ax+AB*Cx)/(AB+BC):Ey=(BC*Ay+AB*Cy)/(AB+BC)
    'AD:y=(Dy-Ay)/(Dx-Ax)*(x-Ax)+Ay=a*x+b
    a=(Dy-Ay)/(Dx-Ax):b=a*(-Ax)+Ay
    'BE:y=(Ey-By)/(Ex-Bx)*(x-Bx)+By=c*x+d
    c=(Ey-By)/(Ex-Bx):d=c*(-Bx)+By
    'Iy=a*Ix+b=c*Ix+d
    Ix=(d-b)/(a-c):Iy=a*Ix+b:rr=Iy
    OI2=(Ix-Ox)*(Ix-Ox)+(Iy-Oy)*(Iy-Oy)
    sa=OI2-(R*R-2*R*rr)
    k1=k1+sa:k2=k2+sa*sa:n=n+1
  next
next
kotae="問題5.平均="&(k1/n)
kotae=kotae&chr(13)&"問題5.分散="&(k2/n-(k1/n)*(k1/n))
msgbox kotae

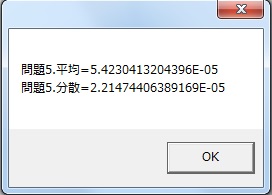
　故に証明された．

「浜田明巳」 02/24 15時32分　受信 更新 3/8

さすがにプログラムだけで解くのは気が引けるので，少しだけですが，数学的に解いてみました．
　また，問題４の逆の証明を忘れていたので，追加します．
問題１
　Ｏは△ＡＢＣの外心なので，ＯＢ＝ＯＣ．
　ＯＬ⊥ＢＣから，ＬはＢＣの中点である．
　同様に，Ｍ，ＮはそれぞれＣＡ，ＡＢの中点である．
　これより，
　　△ＡＮＭ／△ＡＢＣ＝(ＡＮ・ＡＭ)／(ＡＢ・ＡＣ)＝１／４
　　∴△ＡＮＭ＝１／４・Ｓ
　同様に，△ＢＬＮ＝△ＣＭＬ＝１／４・Ｓ
　　∴Ｓ(Ｏ)＝△ＬＭＮ＝△ＡＢＣ−△ＡＮＭ−△ＢＬＮ−△ＣＭＬ
　　　　　　＝(１−１／４・３)Ｓ＝１／４・Ｓ

問題２
　ＢＮ＝ＢＬ＝ｘ，ＣＬ＝ＣＭ＝ｙ，ＡＭ＝ＡＮ＝ｚとすると，
　　△ＬＭＮ＝△ＡＢＣ−△ＢＬＮ−△ＣＬＭ−△ＡＭＮ
　ここで，
　　△ＢＬＮ／△ＡＢＣ＝(ＢＬ・ＢＮ)／(ＢＣ・ＢＡ)＝ｘ^２／{(ｘ＋ｙ)(ｚ＋ｘ)}
　　∴△ＢＬＮ＝ｘ^２／{(ｘ＋ｙ)(ｚ＋ｘ)}・Ｓ
　同様に，
　　△ＣＭＬ＝ｙ^２／{(ｙ＋ｚ)(ｘ＋ｙ)}・Ｓ
　　△ＡＮＭ＝ｚ^２／{(ｚ＋ｘ)(ｙ＋ｚ)}・Ｓ
　　∴Ｓ(Ｉ)＝{１−ｘ^２／{(ｘ＋ｙ)(ｚ＋ｘ)−ｙ^２／{(ｙ＋ｚ)(ｘ＋ｙ)−ｚ^２／{(ｚ＋ｘ)(ｙ＋ｚ)}・Ｓ
　　　　　　＝(ｘ＋ｙ)(ｙ＋ｚ)(ｚ＋ｘ)−ｘ^２(ｙ＋ｚ)−ｙ^２(ｚ＋ｘ)−ｚ^２(ｘ＋ｙ)}／{(ｘ＋ｙ)(ｙ＋ｚ)(ｚ＋ｘ)}・Ｓ
　　　　　　＝(２ｘｙｚ)／{(ｘ＋ｙ)(ｙ＋ｚ)(ｚ＋ｘ)}・Ｓ
　ここで，ａ＝ＢＣ＝ｘ＋ｙ，ｂ＝ＣＡ＝ｙ＋ｚ，ｃ＝ＡＢ＝ｚ＋ｘとすると，
　　(ｘ＋ｙ)(ｙ＋ｚ)(ｚ＋ｘ)＝ａｂｃ
　Ｓ＝(ａｂｃ)／(４Ｒ)から，
　　Ｓ／{(ｘ＋ｙ)(ｙ＋ｚ)(ｚ＋ｘ)}＝１／(４Ｒ)
　Ｈｅｒｏｎの公式から，ｓ＝(ａ＋ｂ＋ｃ)／２＝ｘ＋ｙ＋ｚとすると，
　　Ｓ^２＝ｓ(ｓ−ａ)(ｓ−ｂ)(ｓ−ｃ)＝(ｘ＋ｙ＋ｚ)ｘｙｚ
　Ｓ＝ｓｒから，ｘ＋ｙ＋ｚ＝Ｓ／ｒ
　　∴Ｓ^２＝Ｓ／ｒ・(ｘｙｚ)
　　∴ｘｙｚ＝Ｓｒ
　　∴Ｓ(Ｉ)＝(２Ｓｒ)／(４Ｒ)＝(Ｓｒ)／(２Ｒ)

問題４（逆の証明）
　点Ａを，−１≦Ａｘ＜２，０.２≦Ａｙ＜２.２の範囲でランダムに決める．
　点Ｐを，
　　(Ｂｘ−１，Ａｘ−１の内，大きくない方)≦Ｐｘ≦(Ｃｘ＋１，Ａｘ＋１の内，小さくない方)
　　−１≦Ｐｙ≦(２，Ａｙ＋１の内，小さくない方)
の範囲でシラミつぶしに決めてていき，その都度，
　　｜(cos∠ＬＭＮ−１)・(cos∠ＬＭＮ−(−１))｜＜１０^−１２
である場合，差
　　ＯＰ−Ｒ
を計算し，その平均，分散を求める．
　平均，分散がほぼ０に近い値となれば，Ｐが外接円上にあることとなり，情報数学的に証明される．

randomize:Ax=rnd(1)*3-1:Ay=rnd(1)*2+.2
BC=1:Bx=0:By=0:Cx=BC:Cy=0:Ly=0:Ox=.5*(Bx+Cx)
'ABの垂直二等分線:y=-(Bx-Ax)/(By-Ay)*(x-.5*(Ax+Bx))+.5*(Ay+By)=a*x+b
a=-(Bx-Ax)/(By-Ay):b=a*(-.5*(Ax+Bx))+.5*(Ay+By)
Oy=a*Ox+b
R=sqr((Ox-Ax)*(Ox-Ax)+(Oy-Ay)*(Oy-Ay))
kizami=.01:gosa=10^(-12)
n=0:k1=0:k2=0
Pxmin=Bx-1:Pxmax=Cx+1
if Pxmin>Ax-1 then
  Pxmin=Ax-1
end if
if Ax+1>Pxmax then
  Pxmax=Ax+1
end if
Pymin=-1:Pymax=2
if Ay+1>Pymax then
  Pymax=Ay+1
end if
for Px=Pxmin to Pxmax step kizami
  Lx=Px
  for Py=Pymin to Pymax step kizami
    'AC:y=(Cy-Ay)/(Cx-Ax)*(x-Ax)+Ay=a*x+b
    a=(Cy-Ay)/(Cx-Ax):b=a*(-Ax)+Ay
    'PからACに下ろした垂線:y=-(Cx-Ax)/(Cy-Ay)*(x-Px)+Py=c*x+d
    c=-(Cx-Ax)/(Cy-Ay):d=c*(-Px)+Py
    'My=a*Mx+b=c*Mx+d
    Mx=(d-b)/(a-c):My=a*Mx+b
    'AB:y=(By-Ay)/(Bx-Ax)*(x-Ax)+Ay=a*x+b
    a=(By-Ay)/(Bx-Ax):b=a*(-Ax)+Ay
    'PからABに下ろした垂線:y=-(Bx-Ax)/(By-Ay)*(x-Px)+Py=c*x+d
    c=-(Bx-Ax)/(By-Ay):d=c*(-Px)+Py
    'Ny=a*Nx+b=c*Nx+d
    Nx=(d-b)/(a-c):Ny=a*Nx+b
    LM2=(Mx-Lx)*(Mx-Lx)+(My-Ly)*(My-Ly)
    MN2=(Nx-Mx)*(Nx-Mx)+(Ny-My)*(Ny-My)
    NL2=(Lx-Nx)*(Lx-Nx)+(Ly-Ny)*(Ly-Ny)
    cost=(LM2+MN2-NL2)/(2*sqr(LM2)*sqr(MN2))
    if gosa>abs((cost-1)*(cost-(-1))) then
      sa=sqr((Ox-Px)*(Ox-Px)+(Oy-Py)*(Oy-Py))-R
      k1=k1+sa:k2=k2+sa*sa:n=n+1
    end if
  next
next
kotae="問題4.(逆)平均="&(k1/n)
kotae=kotae&chr(13)&"問題4.(逆)分散="&(k2/n-(k1/n)*(k1/n))
msgbox kotae

　故に証明された．

　今回は問題が多かったように感じます．
　訂正を．参考文献において．
　　現代数学者　→　現代数学社

ＮＯ４「二度漬け白菜」 03/01 14時33分　受信 更新 3/8

問題1： S(O)=S/4 (答)

P=Oのとき，L，M，N は BC，CA，AB の中点であるので，
(△ANMの面積)=(△BLNの面積)=(△CMLの面積)=S/4．
よって，
S(O)=(△ABCの面積)-(△ANMの面積)-(△BLNの面積)-(△CMLの面積)=S/4．

問題2：S(I)=r*S/(2*R) (答)

S=(△IBCの面積)+(△ICAの面積)+(△IABの面積)=(r/2)*(a+b+c)．
S(I)=(△ILMの面積)+(△IMNの面積)+(△INLの面積)．
ここで，
(△ILMの面積)
=(r^2/2)*sin(∠LIM)=(r^2/2)*sin(180°-C)=(r^2/2)*sin(C)
=(r^2/2)*(c/(2*R))．
同様に，(△IMNの面積)=(r^2/2)*(a/(2*R))，(△INLの面積)=(r^2/2)*(b/(2*R))．
よって，
S(I)=(r^2/2)*(1/(2*R))*(a+b+c)=(r/(2*R))*(r/2)*(a+b+c)=r*S/(2*R)．

問題3：
(1)
S(P)=(1/2)*ML*MN*sin(θ)．
∠PLC=∠PMC=90° より，四角形PLCMは円に内接し，その円の直径はCPである．
△CLMに正弦定理を使って，ML=CP*sin(C)．
同様にして，MN=AP*sin(A)．
よって，
S(P)
=(1/2)*ML*MN*sin(θ)
=(1/2)*(CP*sin(C))*(AP*sin(A))*sin(θ)
=(1/2)*AP*CP*sin(θ)*sin(A)*sin(C)．

(2)
∠PCQ=∠PCL+∠QCB．
同じ弧に対する円周角は等しいので，
∠QCB=∠QAB=∠PAN．
四角形AMPNは円に内接する．同じ弧に対する円周角は等しいので，
∠PAN=∠PMN．
四角形PLCMは円に内接する．同じ弧に対する円周角は等しいので，
∠PCL=∠PML．
以上より，∠PCQ=∠PML+∠PMN=θ．
同じ弧に対する円周角は等しいので，
∠PQC=∠AQC=∠ABC=∠B．
△CPQに正弦定理を使って，
CP/sin(B)=PQ/sin(θ)．
よって，CP*sin(ルu梍刋ﾀ・佰w)�ｨ皷遖息．
これを(1)で得られたS(P)の式に代入して，
S( P)=(1/2)*AP*PQ*sin(A)*sin(B)*sin(C)．

(3)
(2)で得られたS(P)の式において，P=Oとした場合を考え，
さらに，S(O)=S/4 を使うと，
S/4=(1/2)*(R^2)*sin(A)*sin(B)*sin(C) となる．
つまり，(1/2)*sin(A)*sin(B)*sin(C)=S/(4*R^2)．
これをS(P)の式に代入して，
S(P)=(S/(4*R^2))*AP*PQ．
ここで，AP*PQについて考える．
P≠Oの場合には，△OAQにスチュワートの定理を使って，
AP*PQ=R^2-d^2となる．これはP=Oの場合にも成り立っている．
よって，S(P)=(S/(4*R^2))*AP*PQ=(1/(4*R^2))*S*(R^2-d^2)．

問題4：
点Pが弧AB上にあるとしても一般性を失わない．
P=AのときはM=N=Aとなるので，L，M，Nは一直線上(つまり直線AL上)にある．
P=Bの場合も同様．
P≠AかつP≠Bとして考える．
四角形PBCAは円に内接するので，∠PBC＋∠PAC=180°．
∠PBC=90°のとき，L(=B)，M(=A)，N は一直線上(つまり直線AB上)にある．
∠PBC＞90°のときは ∠PAC(＜90°)について論ずればよいので，
∠PBC＜90°の場合を考えれば十分．
このとき，∠PAC＞90°であるので、点Mは辺CAの延長上にある．
∠PLB=∠PNB=90°であるので，四角形PBLNは円に内接している．
よって，∠PNL+∠PBL=180°．
四角形PBCAは円に内接するので，∠PBL=∠PAM．
∠PNA=∠PMA=90°であるので，四角形PNAMは円に内接している．
よって，∠PAM=∠PNM．
以上より，∠PNL+∠PNM=180°．
よって L，M，Nは一直線上にある．

問題5：
問題3：(2) で得られたS(P)の式において，P=Iとした場合を考え，
S(I)=r*S/(2*R)を使うことによって，
r*S/(2*R)=(1/(4*R^2))*S*(R^2-OI^2)．
よって，OI^2=R^2-2*R*r．

三角形LMNの面遂u棘C髯・�ｦw)�凾ﾀ点Pと外心との距離) の関数として考えるというのは
興味深いですね。
参考文献の「数学ひとり旅」を読んで、Pがどこにあろうとも
S(P)=(S/(4*R^2))*|R^2-d^2|
が成り立つことを知りました。
しかしこの関係を導くのは、場合分けが多く、
かなり面倒なように思います。
なにかすっきりとした方法があるのでしょうか？

皆さん、問題に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。