�����Q�V�N�X���Q�V��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��325�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF8��30���`9��27����
�m��ߥ���ǰ��̖��������n
�u���w������v���{���Əo�ŎЁi����c���꒘�j��ǂ�ł��āA���[�R�v�E�x���k�[�C�i1654�N�`1705�N�j�����L�̖��������̒l�����߂Ă����Ə����Ă���܂����B
 �@
�@
�Q�l�F�ނ̒�Ƀ��n���E�x���k�[�C�i1667�N�`1748�N�j�����܂��B�I�C���[�i1707�`1783�N�j�̉��t�ɒ�̃��n�������܂��B
NO1�u��x�Ђ����v 08/30
09��49���@��M �X�V 9/27
��325�w�I�ȉ�����̉𑗂�܂��D
��낵�����肢���܂��D
(��)
��1: 2
��2: 6
��3: 26
��4: 150
������ n �Ɛ��� k (0��k) �ɑ��āCA(n,k)�����̂悤�ɒ�`����D
A(n,k)=��[j=0..k]((-1)^j)*comb(n+1,j)*(k-j)^n.
(k>n�̂Ƃ���
A(n,k)=0�ƂȂ�D)
���̂Ƃ��C��[k��0]A(n,k)*t^k �͎��̂悤�ɂȂ�D
��[k��0]A(n,k)*t^k
=��[k��0](��[j=0..k]((-1)^j)*comb(n+1,j)*(k-j)^n)*t^k
=��[k��0](��[j=0..k]((-1)^(k-j))*comb(n+1,k-j)*j^n)*t^k
=��[j��0]��[k��j]((-1)^(k-j))*comb(n+1,k-j)*j^n)*t^k
=��[j��0](j^n)*(t^j)��[k��j]comb(n+1,k-j)*t^(k-j)
=��[j��0](j^n)*(t^j)*(1-t)^(n+1).
����āC
��[j��0](j^n)*(t^j) =
(1-t)^(-n-1)*��[k��0]A(n,k)*t^k.
�C�ӂ̐����� m �ɑ��āC
f(m)=��[k��1](k^m)/(2^k) �Ƃ���ƁC
f(m)=��[k��0](k^m)/(2^k)
=��[j��0](j^m)*((1/2)^j)
=(1-1/2)^(-m-1)*��[k��0]A(m,k)*(1/2)^k
=(1/2)^(-m-1)*��[k=0..m](1/2)^k*(��[j=0..k]((-1)^j)*comb(m+1,j)*(k-j)^m).
���̌v�Z�����g���Čv�Z����ƁC
f(1)=2,f(2)=6,f(3)=26,f(4)=150.
�܂��Ⴆ�C
f(100)
=11133509631364650299699656360843806862971167990688281554425819235539210812744
137555815269127221215916681393895912461647364346849254775983678654845346975177
59492540384054716630.
NO2�uuchinyan�v
08/30 16��11���@��M
�uuchinyan�v
09/04 11��38���@��M �X�V 9/27
������ʓI�ɍl���Ă݂܂��B
�ȉ��ł́Ck�Cn �� 1 �ȏ�̐����Cm �� 0 �ȏ�̐����Cr �� -1 < r < 1 �̎����Ƃ��܂��B
�܂��Clim[n->��]{n^m * r^n} = 0�C�ł��B
����́Cr = 0 �̏ꍇ�͖��炩�Ȃ̂ŁC0 < |r| < 1 �����������ł��B
�����ŁCa �𐳂̎����Ƃ��āC|r| = 1/(1 + a)�C(1 + a)^n = ��[i=0,n]{nCi * a^i}�C�ƂȂ�C
n �� m �����\���ɑ傫�����̐����̏ꍇ�ɂ́C
(1 + a)^n
> nC(m+1) * a^(m+1) = n(n-1)(n-2)�c(n-m)/(m+1)! * a^(m+1)�C
0 < n^m
* |r|^n = n^m/(1 + a)^n < n^m/(nC(m+1) * a^(m+1)) = (m+1)!/a^(m+1) * 1/(n(1
- 1/n)(1 - 2/n)�c(1 - m/n))�C
0 <=
lim[n->��]{n^m * |r|^n} <= (m+1)!/a^(m+1) * lim[n->��]{1/n} *
lim[n->��]{1/(1 - 1/n)(1 - 2/n)�c(1 - m/n))} = 0�C
lim[n->��]{n^m
* |r|^n} = 0�C
������C- |r| <= r <= |r|�C- n^m * |r|^n <=
n^m * r^n <= n^m * |r|^n�C�Ȃ̂ŁC
lim[n->��]{n^m
* r^n} = lim[n->��]{n^m * |r|^n} = 0�C
���ǁCr = 0 ���܂߂āC
lim[n->��]{n^m
* r^n} = 0�C
�������܂��B
���āCSm(n) = ��[k=1,n]{k^m * r^k}�CSm =
lim[n->��]{Sm(n)} = ��[k=1,��]{k^m * r^k}�C�Ƃ��܂��B
m = 0
S0(n) =
��[k=1,n]{r^k} = r(1 - r^n)/(1 - r)�C
S0 =
lim[n->��]{S0(n)} = r/(1 - r)�C
m = 1
S1(n) =
��[k=1,n]{k * r^k}�Cr * S1(n) = ��[k=1,n]{k *
r^(k+1)}�C
(1 -
r)S1(n) = ��[k=1,n]{(k - (k-1))r^k} - n * r^(n+1) = ��[k=1,n]{r^k} - n * r^(n+1)
= S0(n) - n * r^(n+1)�C
(1 - r)S1
= S0 - 0 = S0 = r/(1 - r)�C
S1 = r/(1
- r)^2�C
m = 2
S2(n) =
��[k=1,n]{k^2 * r^k}�Cr * S2(n) = ��[k=1,n]{k^2 *
r^(k+1)}�C
(1 -
r)S2(n) = ��[k=1,n]{(k^2 - (k-1)^2)r^k} - n^2 * r^(n+1)
=
��[k=1,n]{(2k - 1)r^k} - n^2 * r^(n+1)
= 2 *
��[k=1,n]{k * r^k} - ��[k=1,n]{r^k} - n^2 * r^(n+1)
= 2 *
S1(n) - S0(n) - n^2 * r^(n+1)�C
(1 - r)S2
= 2 * S1 - S0 - 0 = 2 * S1 - S0 = 2r/(1 - r)^2 - r/(1 - r)�C
S2 = 2r/(1
- r)^3 - r/(1 - r)^2 = r(r + 1)/(1 - r)^3�C
m = 3
S3(n) =
��[k=1,n]{k^3 * r^k}�Cr * S3(n) = ��[k=1,n]{k^3 *
r^(k+1)}�C
(1 -
r)S3(n) = ��[k=1,n]{(k^3 - (k-1)^3)r^k} - n^3 * r^(n+1)
=
��[k=1,n]{(3k^2 - 3k + 1)r^k} - n^3 * r^(n+1)
= 3 *
��[k=1,n]{k^2 * r^k} - 3 * ��[k=1,n]{k * r^k} + ��[k=1,n]{r^k} - n^3 * r^(n+1)
= 3 *
S2(n) - 3 * S1(n) + S0(n) - n^3 * r^(n+1)�C
(1 - r)S3
= 3 * S2 - 3 * S1 + S0 - 0 = 3 * S2 - 3 * S1 + S0 = 3r(r + 1)/(1 - r)^3 - 3r/(1
- r)^2 + r/(1 - r)�C
S3 = 3r(r
+ 1)/(1 - r)^4 - 3r/(1 - r)^3 + r/(1 - r)^2 = r(r^2 + 4r + 1)/(1 - r)^4�C
m = 4
S4(n) =
��[k=1,n]{k^4 * r^k}�Cr * S34(n) = ��[k=1,n]{k^4 *
r^(k+1)}�C
(1 -
r)S4(n) = ��[k=1,n]{(k^4 - (k-1)^4)r^k} - n^4 * r^(n+1)
=
��[k=1,n]{(4k^3 - 6k^2 + 4k - 1)r^k} - n^4 * r^(n+1)
= 4 *
��[k=1,n]{k^3 * r^k} - 6 * ��[k=1,n]{k^2 * r^k} + 4 * ��[k=1,n]{k * r^k} +-
��[k=1,n]{r^k} - n^4 * r^(n+1)
= 4 *
S3(n) - 6 * S2(n) + 4 * S1(n) - S0(n) - n^4 * r^(n+1)�C
(1 - r)S4
= 4 * S3 - 6 * S2 + 4 * S1 - S0 - 0 = 4 * S3 - 6 * S2 + 4 * S1 - S0
= 4r(r^2 +
4r + 1)/(1 - r)^4 - 6r(r + 1)/(1 - r)^3 + 4r/(1 - r)^2 - r/(1 - r)�C
S4 =
4r(r^2 + 4r + 1)/(1 - r)^5 - 6r(r + 1)/(1 - r)^4 + 4r/(1 - r)^3 - r/(1 - r)^2
= r(r^3 +
11r^2 + 11r + 1)/(1 - r)^5�C
��ʎ������������͓̂�����ł����C�Q�����Ƃ��āC���炩�ɁC
Sm =
(��[i=0,m-1]{mCi * (-1)^(m-1-i) * Si})/(1 - r)
�Ə����܂��ˁB
�����̎��̓��o�ɂ͔������g�����@������܂��B
Sm+1(n) =
��[k=1,n]{k^(m+1) * r^k} = r * d(��[k=1,n]{k^m * r^k})/dr = r * d(Sm(n))/dr�C
Sm+1 =
lim[n->��]{Sm+1(n)} = lim[n->��]{r * d(Sm(n))/dr}�C
�𗘗p���܂��B�����ŁC��ʂɁCf(r) �� r^n ���܂܂Ȃ����Ƃ��āCr^n * f(r) ���l����ƁC
r * d(r^n
* f(r))/dr = nr^n * f(r) + r^n * r * df/dr
�ƂȂ��āC�Ă� r^n ���܂ގ��ɂȂ�܂��B
�����ŁClim[n->��]{n^m * r^n} = 0�C����Cn->�� �ł͂��̍��� 0 �ɂȂ�܂��B
�܂�Cr^n ���܂ލ��́Clim[n->��]{r * d(�c)/dr} �̌v�Z���ʂɂ͌����Ȃ��̂ŁC
�ŏ����炱�̍��������Čv�Z���Ă������ƂɂȂ�܂��B
�ȏ�̂��Ƃ܂��Čv�Z���܂��B
m = 0
S0(n) =
��[k=1,n]{r^k} = r(1 - r^n)/(1 - r) = r/(1 - r) - r^(n+1)/(1 - r)
S0 =
lim[n->��]{S0(n)} = r/(1 - r)�C
���̎����番����܂����Cr^n ���܂ލ��́C����ȍ~�� S0(n) �� r^n ���܂ލ����炵������܂���B
�����ŁC�ȉ��̌v�Z�ŕK�v�Ȃ̂� S0(n) �̍ŏ��̍������ŁC����� S0 �ŁC������ S0 �ɂ� n ������܂���B
�܂�C�ȉ��̌v�Z�ł́Cn->�� �Ȃ��ŁCS0 ������ r
* d(�c)/dr ���邾���ł������ƂɂȂ�܂��B
����́C���ǁCSm+1 = r * d(Sm)/dr�C�Ɠ����ł��B
m = 1
S1 = r *
d(S0)/dr = r * d(r/(1 - r))/dr = r/(1 - r)^2�C
m = 2
S2 = r *
d(S1)/dr = r * d(r/(1 - r)^2)/dr
= r((1 -
r)^2 - r(2(1 - r)(-1)))/(1 - r)^4 = r(r + 1)/(1 - r)^3�C
m = 3
S3 = r *
d(S2)/dr = r * d(r(r + 1)/(1 - r)^3)/dr
= r((2r +
1)(1 - r)^3 - r(r + 1)(3(1 - r)^2(-1)))/(1 - r)^6
= r(r^2 +
4r + 1)/(1 - r)^4�C
m = 4
S4 = r *
d(S3)/dr = r * d(r(r^2 + 4r + 1)/(1 - r)^4)/dr
= r((3r^2
+ 8r + 1)(1 - r)^4 - r(r^2 + 4r + 1)(4(1 - r)^3(-1)))/(1 - r)^8
= r(r^3 +
11r^2 + 11r + 1)/(1 - r)^5�C
������C�v�Z���@�͒P�������炩�ł����C��ʎ������������͓̂�����ł��B
���ǁC
S0 = r/(1
- r)�C
S1 = r/(1
- r)^2�C
S2 = r(r +
1)/(1 - r)^3�C
S3 = r(r^2
+ 4r + 1)/(1 - r)^4�C
S4 = r(r^3
+ 11r^2 + 11r + 1)/(1 - r)^5�C
�ɂȂ�܂��B
��P�F
S1 �� r = 1/2 �Ƃ���悭�C
S1 =
(1/2)/(1 - 1/2)^2 = 2
��Q�F
S2 �� r = 1/2 �Ƃ���悭�C
S2 =
(1/2)(1/2 + 1)/(1 - 1/2)^3 = 2(1 + 2) = 6
��R�F
S3 �� r = 1/2 �Ƃ���悭�C
S3 =
(1/2)((1/2)^2 + 4(1/2) + 1)/(1 - 1/2)^4 = 2(1 + 8 + 4) = 26
��S�F
S4 �� r = 1/2 �Ƃ���悭�C
S4 =
(1/2)((1/2)^3 + 11(1/2)^2 + 11(1/2) + 1)/(1 - 1/2)^5 = 2(1 + 22 + 44 + 8) = 150
(�ʉ�)
Sm =
(��[i=0,m-1]{mCi * (-1)^(m-1-i) * Si})/(1 - r)
�𗘗p���܂��B���̎��� S0 = r/(1 - r) �� r = 1/2 �Ŏg���܂��B
Sm = 2 *
��[i=0,m-1]{mCi * (-1)^(m-1-i) * Si}�C
S0 = 1
��P�F
S1 = 2 *
(1C0 * (-1)^0 * S0) = 2 * 1 = 2
��Q�F
S2 = 2 *
(2C0 * (-1)^1 * S0 + 2C1 * (-1)^0 * S1) = 2 * (- 1 + 4) = 2 * 3 = 6
��R�F
S3 = 2 *
(3C0 * (-1)^2 * S0 + 3C1 * (-1)^1 * S1 + 3C2 * (-1)^0 * S2)
= 2 * (1 -
6 + 18) = 2 * 13 = 26
��S�F
S4 = 2 *
(4C0 * (-1)^3 * S0 + 4C1 * (-1)^2 * S1 + 4C2 * (-1)^1 * S2 + 4C3 * (-1)^0 * S3)
= 2 * (- 1
+ 8 - 36 + 104) = 2 * 75 = 150
(�l�@)
���̌�C��ʎ������������l���Ă݂܂����B���܂ЂƂ̊���������܂����C�ꉞ�C�����Ă����܂��B
�������g�����@�ōl���܂��B
Sm = r *
d(Sm-1)/dr�C
S0 = r/(1
- r) = - 1 + 1/(1 - r)�C
S1 = r *
d(S0)/dr = r * d(- 1 + 1/(1 - r))/dr
= r/(1 -
r)^2 = - 1/(1 - r) + 1/(1 - r)^2�C
S2 = r *
d(S1)/dr = r * d(- 1/(1 - r) + 1/(1 - r)^2)/dr
= - r/(1 -
r)^2 + 2r/(1 - r)^3 = 1/(1 - r) - 3/(1 - r)^2 + 2/(1 - r)^3
S3 = r *
d(S2)/dr = r * d(1/(1 - r) - 3/(1 - r)^2 + 2/(1 - r)^3)/dr
= r/(1 -
r)^2 - 6r/(1 - r)^3 + 6r/(1 - r)^4
= - 1/(1 -
r) + 7/(1 - r)^2 - 12/(1 - r)^3 + 6/(1 - r)^4�C
S4 = r *
d(S3)/dr = r * d(- 1/(1 - r) + 7/(1 - r)^2 - 12/(1 - r)^3 + 6/(1 - r)^4)/dr
= - r/(1 -
r)^2 + 14r/(1 - r)^3 - 36r/(1 - r)^4 + 24r/(1 - r)^5
= 1/(1 -
r) - 15/(1 - r)^2 + 50/(1 - r)^3 - 60/(1 - r)^4 + 24/(1 - r)^5
�c
�����̌v�Z����Cm >= 1 �� Sm = ��[n=1,m+1]{a(m,n)/(1 -
r)^n}�C�Ƃ����āC
a(m+1,n) =
(n-1) * a(m,n-1) - n * a(m,n)�Ca(0,1) = 1�Cn <= 0 ���� n >= m+2 �� a(m,n) = 0�C
�ƂȂ�܂��B���̑Q�����͎��̂悤�ɂ��ĉ������Ƃ��ł��܂��B
a(m+1,1) =
- a(m,1)�Ca(0,1) = 1�C
a(m,1) =
(-1)^m�C
a(m+1,2) =
a(m,1) - 2 * a(m,2) = (-1)^m - 2 * a(m,2)�C
a(m+1,2)/(-2)^(m+1)
- a(m,2)/(-2)^m = 1/(-2) * (1/2)^m�Ca(0,2) = 0�C
a(m,2)/(-2)^m
= 1/(-2) * ��[k=0,m-1]{(1/2)^k} = 1/(-2) * (1 - (1/2)^m)/(1 - 1/2) = (1/2)~m - 1�C
a(m,2) =
(-1)^m * (1 - 2^m)�C
a(m+1,3) =
2 * a(m,2) - 3 * a(m,3) = 2 * (-1)^m * (1 - 2^m) - 3 * a(m,3)�C
a(m+1,3)/(-3)^(m+1)
- a(m,3)/(-3)^m = 2/(-3) * ((1/3)^m - (2/3)^m)�Ca(1,3) = 0�C
a(m,3)/(-3)^m
= 2/(-3) * ��[k=1,m-1]{(1/3)^k - (2/3)^k}
= 2/(-3) *
((1/3)(1 - (1/3)^(m-1))/(1 - 1/3) - (2/3)(1 - (2/3)^(m-1))/(1 - 2/3))
= 1/(-3) *
((1 - (1/3)^(m-1)) - 4(1 - (2/3)^(m-1)))
= (1/3)^m
- 2(2/3)^m + 1
a(m,3) =
(-1)^m * (1 - 2 * 2^m + 3^m)�C
a(m+1,4) =
3 * a(m,3) - 4 * a(m,4) = 3 * (-1)^m * (1 - 2 * 2^m + 3^m) - 4 * a(m,4)�C
a(m+1,4)/(-4)^(m+1)
- a(m,4)/(-4)^m = 3/(-4) * ((1/4)^m - 2 * (2/4)^m + (3/4)^m)�Ca(2,4) = 0�C
a(m,4)/(-4)^m
= 3/(-4) * ��[k=2,m-1]{(1/4)^k - 2 * (2/4)^k + (1/4)^k}
= 3/(-4) *
((1/4)^2 * (1 - (1/4)^(m-2))/(1 - 1/4) - 2 * (2/4)^2 * (1 - (2/4)^(m-2))/(1 -
2/4)
+ (3/4)^2
* (1 - (3/4)^(m-2))/(1 - 3/4))
= 1/(-4^2)
* ((1 - (1/4)^(m-2)) - 12(1 - (2/4)^(m-2)) + 27(1 - (3/4)^(m-2)))
= (1/4)^m
- 3(2/4)^m + 3(3/4)^m - 1
a(m,4) =
(-1)^m * (1 - 3 * 2^m + 3 * 3^m - 4^m)�C
�c
�����܂Ōv�Z����ƁC
a(m,n) =
(-1)^m * ��[k=1,n]{(-1)^(k-1) * (n-1)C(k-1) * k^m}�C
�ł͂Ȃ����C�Ɨ\�z�ł��܂��B����𐔊w�I�A�[�@�Ŋm�F���܂��傤�B
n = 1 �` 4 �͍��܂ł̌v�Z��萬������͖̂��炩�B
n-1 �Ő������Ƃ��āC
a(m+1,n) =
(n-1) * a(m,n-1) - n * a(m,n)
= (n-1) *
(-1)^m * ��[k=1,n-1]{(-1)^(k-1) * (n-2)C(k-1) * k^m} - n * a(m,n)�C
a(m+1,n)/(-n)^(m+1)
- a(m,n)/(-n)^m
=
(n-1)/(-n) * ��[k=1,n-1]{(-1)^(k-1) * (n-2)C(k-1) * (k/n)^m}�Ca(n-2,n) = 0�C
a(m,n)/(-n)^m
= (n-1)/(-n) * ��[i=n-2,m-1]{��[k=1,n-1]{(-1)^(k-1) * (n-2)C(k-1) * (k/n)^i}}
= (n-1)/(-n)
* ��[k=1,n-1]{(-1)^(k-1) * (n-2)C(k-1) * (k/n)^(n-2) * (1 - (k/n)^(m -(n-2)))/(1
- k/n)}
= (n-1) *
��[k=1,n-1]{(-1)^k * (n-2)C(k-1) * ((k/n)^(n-2) - (k/n)^m)/(n-k)}
=
��[k=1,n-1]{(-1)^k * (n-1)C(k-1) * ((k/n)^(n-2) - (k/n)^m))}
=
��[k=1,n-1]{(-1)^(k-1) * (n-1)C(k-1) * (k/n)^m)}
+
��[k=1,n-1]{(-1)^k * (n-1)C(k-1) * (k/n)^(n-2)}
�����ŁC��Q���́C
��[k=1,n-1]{(-1)^k * (n-1)C(k-1) * (k/n)^(n-2)}
=
��[k=0,n-1]{(-1)^k * nCk * k^(n-1)}/n^(n-1)
�Ə����C���̕��q�́C
(1 - x)^n
= ��[k=0,n]{(-1)^k * nCk * x^k)}
�� x �Ŕ����� x ���|����Cx *
d/dx�C�� n-1 ��s���� x = 1 �Ƃ��������̂��� k = n �����������ł��B
k = n �����ꂽ�S�̂́C(1 - x)^n �ɑ��� n-1 ��̔����ł� 1 - x ���c���Ă��܂��̂ŁCx = 1 �� 0 �ł��B
k = n �̍��͂��̑���� (-1)^n * n^(n-1) �ƂȂ�̂ŁC���ǁC
��[k=0,n-1]{(-1)^k * nCk * k^(n-1)} + (-1)^n * n^(n-1) = 0�C
��[k=0,n-1]{(-1)^k * nCk * k^(n-1)} = (-1)^(n-1) * n^(n-1)�C
�ł��B�����ŁC
��[k=1,n-1]{(-1)^k * (n-1)C(k-1) * (k/n)^(n-2)}
=��[k=0,n-1]{(-1)^k
* nCk * k^(n-1)}/n^(n-1)
=
(-1)^(n-1) * n^(n-1)/n^(n-1) = (-1)^(n-1) = (-1)^(n-1) * (n-1)C(n-1) * (n/n)^m�C
a(m,n)/(-n)^m
=
��[k=1,n-1]{(-1)^(k-1) * (n-1)C(k-1) * (k/n)^m)}
+
��[k=1,n-1]{(-1)^k * (n-1)C(k-1) * (k/n)^(n-2)}
=
��[k=1,n-1]{(-1)^(k-1) * (n-1)C(k-1) * (k/n)^m)}
+
(-1)^(n-1) * (n-1)C(n-1) * (n/n)^m
=
��[k=1,n]{(-1)^(k-1) * (n-1)C(k-1) * (k/n)^m)}�C
a(m,n) =
(-1)^m * ��[k=1,n]{(-1)^(k-1) * (n-1)C(k-1) * k^m)}
�ƂȂ��āC�������܂��B����ŁCa(m,n) �̈�ʎ������܂�܂����B�����ŁC
Sm =
��[n=1,m+1]{(-1)^m * ��[k=1,n]{(-1)^(k-1) * (n-1)C(k-1) * k^m)}/(1 - r)^n}�C
�ƂȂ�܂��B�ꉞ�͋��܂����Ƃ͂����ȒP�ł͂Ȃ��ł��ˁB
�Ȃ��C���̎����g���č���̖��������ƁCr = 1/2�C1/(1 - r) = 2�C�Ȃ̂ŁC
S1 = -
1/(1 - r) + 1/(1 - r)^2
-> - 2
+ 2^2 = - 2 + 4 = 2�C
S2 = 1/(1
- r) - 3/(1 - r)^2 + 2/(1 - r)^3
-> 2 -
3 * 2^2 + 2 * 2^3 = 2 - 12 + 16 = 6�C
S3 = -
1/(1 - r) + 7/(1 - r)^2 - 12/(1 - r)^3 + 6/(1 - r)^4
-> - 2
+ 7 * 2^2 - 12 * 2^3 + 6 * 2^4 = - 2 + 28 - 96 + 96 = 26�C
S4 = 1/(1
- r) - 15/(1 - r)^2 + 50/(1 - r)^3 - 60/(1 - r)^4 + 24/(1 - r)^5
-> 2 -
15 * 2^2 + 50 * 2^3 - 60 * 2^4 + 24 * 2^5= 2 - 60 + 400 - 960 + 768 = 150
�ƂȂ�܂��B���R�ł����C�ȑO�̌��ʂƈ�v���܂��B
(���z)
�������g������@�́C��w���x���̒m�����g���C
S0 =
��[k=1,��]{r^k} = r/(1 - r)�C
���C�������a 1 �������C���͈̔͂ň�l��Ύ������邱�Ƃ���C��茵�����e�Ղɂ����邱�Ƃł��B
�����ł́C������g�킸�ɁC���Z���x���ł܂Ƃ߂Ă݂܂����B
���������̗��_�͎����̌����Ȓ�`�Ƒ��܂��Ċ��������o�܂�����C
���[�R�u�E�x���k�[�C���������͂܂����W�r��Ǝv���܂��B
��X�͑����̐�l�����̉b�q�̂������ő啪�y�������Ă�����Ă���ȁC�Ɖ��߂Ďv���܂��B
�Ȃ��C��L�̕��@�ł͈�ʎ����������������ʂ̒l�����߂�͓̂�����ł��B
�������܂��H�v���Ȃ����̂��ȁC�Ƃ��v���܂��B
���̌�C��ʎ��̓��o�����l�@���܂����B�����C���܂������Ă���Ƃ͂����������̂ł����B
NO3�u���N���̂�������v 08/31 14��13���@��M �X�V 9/27
325�@���N���̂�������
���P
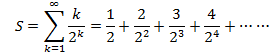
�Ƃ����AS���� ![]() �������ƁA�������䋉���ɂȂ�܂��B
�������ƁA�������䋉���ɂȂ�܂��B
![]()
![]()
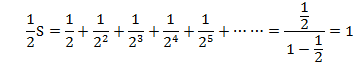
����āA
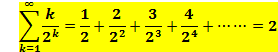
���2
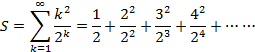
�Ƃ����A���1�Ɠ��l�ɍl���܂��B
![]()
![]()
![]()
![]()
�����ŁA
![]()
�Ƃ����܂��B
![]()
![]()
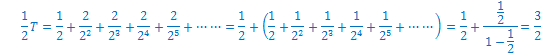
����āA
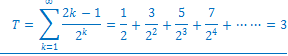
���̒l��m���Ď��iA�j�ɑ�����A�v�Z���܂��B
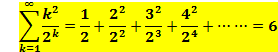
���3
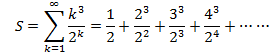
�Ƃ����܂��B
![]()
![]()
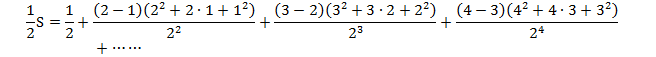
![]()
![]()
![]()
�����ŁA
![]()
�Ƃ����܂��B
![]()
![]()
![]()
![]()
����āA
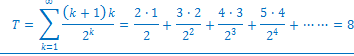
���̒l��m���Ď��iB�j�ɑ�����A�v�Z���܂��B
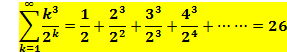
���4
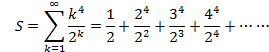
�Ƃ����܂��B
![]()
![]()
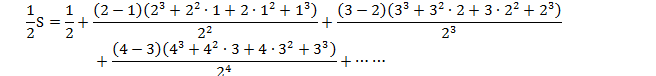
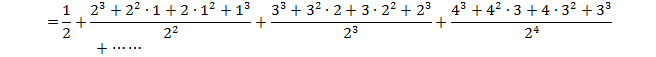
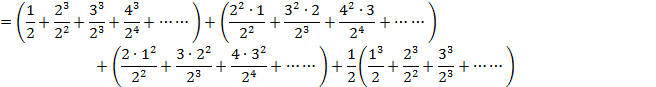
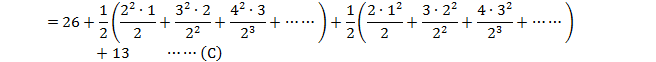
�����ŁA
![]()
�Ƃ����܂��B
���炩���߁A
![]()
���ӂ܂��Ď��̌v�Z�����܂��B
![]()
![]()
![]()
![]()
![]()
����āA
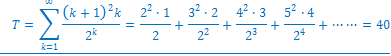
���ɁA
![]()
�Ƃ����܂��B
���炩���߁A
![]()
���ӂ܂��Ď��̌v�Z�����܂�
![]()
![]()
![]()
![]()
![]()
����āA
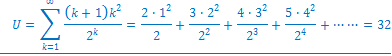
���̒l��m���Ď��iC�j�ɑ�����A�v�Z���܂��B
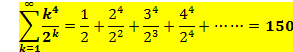
NO4�u�l�c�����v
09/02 16��35���@��M �X�V 9/27
VBSCRIPT�ɂĈʗ������Ȃ��Ƃ���܂Ōv�Z���C�������߂��D
s1=0
s2=0
s3=0
s4=0
for j=1 to 1000
s1=s1+j/2^j
s2=s2+j*j/2^j
s3=s3+j*j*j/2^j
s4=s4+j*j*j*j/2^j
next
msgbox s1&chr(13)&s2&chr(13)&s3&chr(13)&s4
���ꂼ�ꕔ���a�̋Ɍ������߂�悢�D
��P�D�����P�Ƃ���D
�@�悎�����a
�@�@�r�����P�^�Q�{�Q�^�Q�Q�{�R�^�Q�R�{�E�E�E�{���^�Q���E�E�E(1)
�ɂ��āC
�@�@�P�^�Q�E�r�����P�^�Q�Q�{�Q�^�Q�R�{�E�E�E�{(���|�P)�^�Q���{���^�Q���{�P�E�E�E(2)
�@(1)�|(2)���C
�@�@�P�^�Q�E�r�����P�^�Q�{�P�^�Q�Q�{�P�^�Q�R�{�E�E�E�{�P�^�Q���|���^�Q���{�P
�@�@�@�@�@�@�@�@���P�^�Q�E{�P�|(�P�^�Q)��}�^(�P�|�P�^�Q)�|���^�Q���{�P
�@�@�@�@�@�@�@�@���P�|(�P�^�Q)���|���^�Q���{�P
�@�@���r�����Q{�P�|(�P�^�Q)��}�|���^�Q���E�E�E(3)
�@�����ŁC�藝�Ƃ����P���C
�@�@�Q����(�P�{�P)�������b�O�{���b�P�{���b�Q�{�E�E�E�{���b�������b�Q��{��(���|�P)}�^�Q���O
�@�@���O���P�^�Q�����Q�^{��(���|�P)}
�@�@���O�����^�Q�����Q�^(���|�P)���O�i�������j
�@�͂��݂����̌������C
�@�@lim���������^�Q�����O
�@(3)����C
�@�@lim�������r����lim������[�Q{�P�|(�P�^�Q)��}�|���^�Q��]���Q�E�E�E(��)
��Q�D�����Q�Ƃ���D
�@�悎�����a
�@�@�r�����P�Q�^�Q�{�Q�Q�^�Q�Q�{�R�Q�^�Q�R�{�S�Q�^�Q�S�{�E�E�E�{���Q�^�Q���E�E�E(1)
�ɂ��āC
�@�@�P�^�Q�E�r�����P�Q�^�Q�Q�{�Q�Q�^�Q�R�{�R�Q�^�Q�S�{�E�E�E�{(���|�P)�Q�^�Q���{���Q�^�Q���{�P�E�E�E(2)
�@(1)�|(2)���C
�@�@�P�^�Q�E�r�����P�^�Q�{�R�^�Q�Q�{�T�^�Q�R�{�V�^�Q�S�{�E�E�E�{(�Q���|�P)�^�Q���|���Q�^�Q���{�P�E�E�E(3)
�@�@���r�����P�{�R�^�Q�{�T�^�Q�Q�{�V�^�Q�R�{�E�E�E�{(�Q���|�P)�^�Q���|�P�|���Q�^�Q���E�E�E(4)
�@(4)�|(3)���C
�@�@�P�^�Q�E�r�����P�{�Q�^�Q�{�Q�^�Q�Q�{�Q�^�Q�R�{�E�E�E�{�Q�^�Q���|�P
�@�@�@�@�@�@�@�@�@�@�{(�|���Q�|�Q���{�P)�^�Q���{���Q�^�Q���{�P
�@�@�@�@�@�@�@�@���P�{�P�{�P�^�Q�{�P�^�Q�Q�{�E�E�E�{�P�^�Q���|�Q�{{�Q(�|���Q�|�Q���{�P)�{���Q)�^�Q���{�P
�@�@�@�@�@�@�@�@���P�{{�P�|(�P�^�Q)���|�P}�^(�P�|�P�^�Q)�{(�|���Q�|�S���{�Q)�^�Q���{�P
�@�@�@�@�@�@�@�@���P�{�Q{�P�|(�P�^�Q)���|�P}�{(�|���Q�|�S���{�Q)�^�Q���{�P
�@�@�@�@�@�@�@�@���R�|(�P�^�Q)���|�Q�{(�|���Q�|�S���{�Q)�^�Q���{�P
�@�@���r�����U�|(�P�^�Q)���|�R�{(�|���Q�|�S���{�Q)�^�Q���E�E�E(5)
�@�����ŁC�藝�Ƃ����Q���C
�@�@�Q�������b�O�{���b�P�{���b�Q�{���b�R�{�E�E�E�{���b�������b�R��{��(���|�P)(���|�Q)}�^�U���O
�@�@���O���P�^�Q�����U�^{��(���|�P)(���|�Q)}
�@�@���O���b(�|���Q�|�S���{�Q)�^�Q���b���U�b(�|���Q�|�S���{�Q)�^{��(���|�P)(���|�Q)}�b
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���U�b(�|�P�|�S�^���{�Q�^���Q)�^{(�P�|�P�^��)(���|�Q)}�b���O�i�������j
�@�͂��݂����̌������C
�@�@lim������(�|���Q�|�S���{�Q)�^�Q�����O
�@(5)����C
�@�@lim�������r����lim������{�U�|(�P�^�Q)���|�R�{(�|���Q�|�S���{�Q)�^�Q��}���U�E�E�E(��)
��R�D
�@��P�C�Q�Ɠ��l�ɁClim������(���̂Q����)�^�Q����lim������(���̂R����)�^�Q�����O�ł���D
�@�����ŁC�q��(��)��(���̂�����)�^�Q���ilim�������q��(��)���O�j�Ƃ���D
�@�����R�Ƃ���D
�@�悎�����a
�@�@�r�����P�R�^�Q�{�Q�R�^�Q�Q�{�R�R�^�Q�R�{�S�R�^�Q�S�{�T�R�^�Q�T�{�E�E�E�{���R�^�Q���E�E�E(1)
�ɂ��āC
�@�@�P�^�Q�E�r�����P�R�^�Q�Q�{�Q�R�^�Q�R�{�R�R�^�Q�S�{�S�R�^�Q�T�{�E�E�E�{(���|�P)�R�^�Q���{���R�^�Q���{�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E(2)
�@(1)�|(2)���C
�@�@�P�^�Q�E�r�����P�^�Q�{�V�^�Q�Q�{�P�X�^�Q�R�{�R�V�^�Q�S�{�U�P�^�Q�T�{�E�E�E�{(�R���Q�|�R���{�P)�^�Q��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|���R�^�Q���{�P�E�E�E(3)
�@�@���r�����P�{�V�^�Q�{�P�X�^�Q�Q�{�R�V�^�Q�R�{�U�P�^�Q�S�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�@�@�{(�R���Q�|�R���{�P)�^�Q���|�P�|���R�^�Q���E�E�E(4)
�@(4)�|(3)���C
�@�@�P�^�Q�E�r�����P�{�U�^�Q�{�P�Q�^�Q�Q�{�P�W�^�Q�R�{�Q�S�^�Q�S�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�{[(�R���Q�|�R���{�P)�|{�R(���|�P)�Q�|�R(���|�P)�{�P}]�^�Q���|�P�{�q�P(��)
�@�@�@�@�@�@�@�@���P�{�R{�P�{�Q�^�Q�{�R�^�Q�Q�{�S�^�Q�S�{�E�E�E�{(���|�P)�^�Q���|�Q}�{�q�P(��)
�@�@���r�����Q�{�U{�P�{�Q�^�Q�{�R�^�Q�Q�{�S�^�Q�R�{�E�E�E�{(���|�P)�^�Q���|�Q}�{�Q�q�P(��)�E�E�E(5)
�@�@���P�^�Q�E�r�����P�{�U{�P�^�Q�{�Q�^�Q�Q�{�R�^�Q�R�{�S�^�Q�S�{�E�E�E�{(���|�P)�^�Q���|�P}�{�q�P(��)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E(6)
�@(5)�|(6)���C
�@�@�P�^�Q�E�r�����P�{�U{�P�{�P�^�Q�{�P�^�Q�Q�{�P�^�Q�R�{�E�E�E�{�P�^�Q���|�Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|(���|�P)�^�Q���|�P}�{�q�P(��)
�@�@�@�@�@�@�@���P�{�U�E{�P�|(�P�^�Q)���|�P}�^(�P�|�P�^�Q)�{�q�Q(��)
�@�@�@�@�@�@�@���P�{�P�Q{�P�|(�P�^�Q)���|�P}�{�q�Q(��)
�@�@�@�@�@�@�@���P�R�|�P�Q(�P�^�Q)���|�P�{�q�Q(��)
�@�@���r�����Q�U�|�Q�S(�P�^�Q)���|�P�{�Q�q�Q(��)���Q�U�i�������j
��S�D�����\���傫�Ȑ������Ƃ���D
�@�悎�����a
�@�@�r�����P�S�^�Q�{�Q�S�^�Q�Q�{�R�S�^�Q�R�{�S�S�^�Q�S�{�T�S�^�Q�T�{�U�S�^�Q�U�{�E�E�E�{���S�^�Q���E�E�E(1)
�ɂ��āC
�@�@�P�^�Q�E�r�����P�S�^�Q�Q�{�Q�S�^�Q�R�{�R�S�^�Q�S�{�S�S�^�Q�T�{�E�E�E�{(���|�P)�S�^�Q���{���S�^�Q���{�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E(2)
�@(1)�|(2)���C
�@�@�P�^�Q�E�r�����P�^�Q�{�P�T�^�Q�Q�{�U�T�^�Q�R�{�P�V�T�^�Q�S�{�R�U�X�^�Q�T�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{(�S���R�|�U���Q�{�S���|�P)�^�Q���|���S�^�Q���{�P�E�E�E(3)
�@�@���r�����P�{�P�T�^�Q�{�U�T�^�Q�Q�{�P�V�T�^�Q�R�{�R�U�X�^�Q�S�{�U�V�P�^�Q�T�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�@�@�{(�S���R�|�U���Q�{�S���[�P)�^�Q���|�P�|���S�^�Q���E�E�E(4)
�@(4)�|(3)���C
�@�@�P�^�Q�E�r�����P�{�P�S�^�Q�{�T�O�^�Q�Q�{�P�P�O�^�Q�R�{�P�X�S�^�Q�S�{�R�O�Q�^�Q�T�{�E�E�E
�@�@�@�@�@�@�@�@�{[(�S���R�|�U���Q�{�S���|�P)�|{�S(���|�P)�R�|�U(���|�P)�Q�{�S(���|�P)�|�P}]�^�Q���|�P
�@�@�@�@�@�@�@�@�{�q�P(��)
�@�@�@�@�@�@�@�@�@���P�{�V�{�Q�T�^�Q�{�T�T�^�Q�Q�{�X�V�^�Q�R�{�P�T�P�^�Q�S�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�{(�U���Q�|�P�Q���{�V)�^�Q���|�Q�{�q�P(��)�E�E�E(5)
�@�@���r�����Q�E�W�{�Q�T�{�T�T�^�Q�{�X�V�^�Q�Q�{�P�T�P�^�Q�R�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�@�@�{(�U���Q�|�P�Q���{�V)�^�Q���|�R�{�Q�q�P(��)�E�E�E(6)
�@(6)�|(5)���C
�@�@�P�^�Q�E�r�����R�R�{�R�O�^�Q�{�S�Q�^�Q�Q�{�T�S�^�Q�R�{�E�E�E
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{[{(�U���Q�|�P�Q���{�V)�|{�U(���|�P)�Q�|�P�Q(���|�P)�{�V}]�^�Q���|�R�{�q�Q(��)
�@�@�@�@�@�@�@�@���R�R�{�P�T�{�Q�P�^�Q�{�Q�V�^�Q�Q�{�E�E�E�{(�U���|�X)�^�Q���|�S�{�q�R(��)
�@�@���r�����Q�E�S�W�{�Q�P�{�Q�V�^�Q�{�E�E�E�{(�U���|�X)�^�Q���|�T�{�Q�q�R(��)
�@�@�@�@�@���X�U�{�R{�V�{�X�^�Q�{�E�E�E�{(�Q���|�R)�^�Q���|�T}�{�Q�q�R(��)�E�E�E(7)
�@�@���P�^�Q�E�r�����S�W�{�R{�V�^�Q�{�X�^�Q�Q�{�E�E�E�{(�Q���|�R)�^�Q���|�S}�{�q�R(��)�E�E�E(8)
�@(7)�|(8)���C
�@�@�P�^�Q�E�r�����S�W�{�R(�V�{�Q�^�Q�{�Q�^�Q�Q�{�E�E�E�{�Q�^�Q���|�S)�{�q�S(��)
�@�@�@�@�@�@�@�@���S�W�{�Q�P�{�R(�P�{�P�^�Q�{�E�E�E�P�^�Q���|�T)�{�q�S(��)
�@�@�@�@�@�@�@�@���U�X�{�R�E{�P�|(�P�^�Q)���|�S}�^(�P�|�P�^�Q)�{�q�S(��)
�@�@�@�@�@�@�@�@���U�X�{�U{�P�|(�P�^�Q)���|�S}�{�q�S(��)
�@�@�@�@�@�@�@�@���V�T�|�U(�P�^�Q)���|�S�{�q�S(��)
�@�@���r�����P�T�O�|�P�Q(�P�^�Q)���|�S�{�Q�q�S(��)���P�T�O�i�������j
NO5�u�Ӱ��݁v
09/02 17��23���@��M �X�V 9/27
����͍ŏ��̂Q�₪�������Ǝv���܂��̂ł����܂ł��� Orz
(1)
1/2+2/2^2+3/2^3+4/2^4+�c
+1/2^2+1/2^3+�c�E�E�E(1/2)*S
+1/2^3+1/2^4+�c�E�E�E(1/2^2)*S
+1/2^4+�c�E�E�E(1/2^3)*S
�c
=S*(S+1)
=1*2=2
(2)
1/2+2^2/2^2+3^3/2^3+�c
1+1/2+1/2^2+�c=1+S=2
+2*(1/2++1/2^2+�c�E�E�ES
+2*(1/2^2+1/2^3+�c�E�E�ES/2
+2*(1/2^3+1/2^4+�c�E�E�ES/2^2
=S*(1+1+1/2+1/2^2+�c)
=S*(2+S)
=1*3=3
(3),(4) �́A�����炭�A4,5 �ɂȂ�̂��낤���ǂ킩�炸�c^^;
�Ĕ����̂悤�ɃΗ��݂��Ǝv���Ă܂������c���W�̂悤�ł��� �c^^
�����̗���F�c�O�Ȃ���i�Q�j�͐����Ɏ����āE�E�E��
NO6�u�ɂ���Z12�v 09/09 23��41���@��M
�X�V 9/27
����
�@�@a=��k=1�`��1/2k=1/2+1/22+1/23+1/24+1/25+�E�E�E�E=(1/2)/(1-1/2)=1(���䋉���̌���)
�A�@np-(n-1)p=
np-��i=0�`p�op C p -i (-1) i-1np�p=-��i=1�`p�op C p -i (-1) inp-1�p�i�藝�j�H
��1�@���̖��͐悸���ό`�ŕ��ʂɍl���܂���
��k=1�`��k/2k= 1/2+2/22+3/23+4/24+5/25+�E�E�E�E
�@�@�@�@�@= 1/2+1/22+1/23+1/24+1/25+�E�E�E�E
+ 1/22+1/23+1/24+1/25+�E�E�E�E
+�@
1/23+1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+
+1/25+�E�E�E�E
�E
�E
�@�@�@�@�@= 1/2+1/22+1/23+1/24+1/25+�E�E�E�E
+ 1/2(1/2+1/22+1/23+1/24+�E�E�E�E)
+ 1/22(1/2+1/22+1/23+�E�E�E�E)
+
1/23(1/2+1/22+�E�E�E�E)
+
1/24(1/2+�E�E�E�E)
�E
�E
��k=1�`��1/2k=1�E�E�E�����@���
=a+(1/2+2/22+3/23+4/24+5/25+�E�E�E�E)a=a+a2=2�E�E�E��
�������A����ɂ�����������܂��A�u�E�E�E�v���g��Ȃ��ŏ�����
��k=1�`��k/2k=(��k=1�`��1/2k)(1+(��k=1�`��1/2k )(��k=1�`��1/2k))=2�ƂȂ�܂��B�i�֑��j
��2�@��1�Ɠ��l�Ɏ��ό`�ōl����Ǝ��̂悤�ɂȂ�܂��B
��k=1�`��k2/2k=
1/2+22/22+32/23+42/24+52/25+�E�E�E�E
�@�@�@�@�@= 1/2+1/22+1/23+1/24+1/25+�E�E�E�E
+ 1/22+1/23+1/24+1/25+�E�E�E�E
+ 1/22+1/23+1/24+1/25+�E�E�E�E
+ 1/22+1/23+1/24+1/25+�E�E�E�E
+�@
1/23+1/24+1/25+�E�E�E�E
+�@
1/23+1/24+1/25+�E�E�E�E
+�@
1/23+1/24+1/25+�E�E�E�E
+�@
1/23+1/24+1/25+�E�E�E�E
+�@
1/23+1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+ 1/24+1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
+
1/25+�E�E�E�E
�E
�E
�@�@�@�@�@=
a(12-0)+a(22-1)�E1/2+ a(32-22)�E1/22+
a(42-32)�E1/23+ a(52-42)�E1/24+�E�E�E�E
�@�@�@�@�@= 1+(22-1)�E1/2+(32-22)�E1/22+(42-32)�E1/23+(52-42)�E1/24+�E�E�E�E
������n2-(n-1)2�̐�����l�����
�����A����2n-1�ƂȂ�̂�n=1����l����Ɗ��ƂȂ�܂��B
�����
��k=1�`��k2/2k= (1/2)0+3(1/2)1+5(1/2)2+7(1/2)3+9(1/2)
4+11(1/2)5+�E�E�E�E=��k=1�`��(2k-1)/2(k-1)
��k=1�`��k2/2k=��k=1�`��2k/2(k-1) -��k=1�`��1/2(k-1) =4��k=1�`��k/2k –2(��k=1�`��1/2k)
��k=1�`��k/2k=2�E�E�E��1���
��k=1�`��1/2k=1�E�E�E�����@���
��k=1�`��k2/2k=4��k=1�`��k/2k –2(��k=1�`��1/2k) =4�~2�|2�~1��6�E�E�E�E�E�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
��3�@��2�Ԏ��Ɠ��l�ɕ\������Ǝ��̂悤�ɂȂ�܂��B
��k=1�`��k3/2k�@= a(13-0)+a(23-1)�E1/2+ a(33-23)�E1/22+ a(43-33)�E1/23+ a(53-43)�E1/24+�E�E�E�E
������n3-(n-1)3�̐���͏����A����
3n2-3n+1
�����
��k=1�`��k3/2k�@=3��k=1�`��k2/2k-1�|3��k=1�`��k/2k-1+��k=1�`��1/2k-1
��k=1�`��k2/2k=6�E�E�E��2���
��k=1�`��k/2k=2�E�E�E��1���
��k=1�`��1/2k=1�E�E�E�������
��k=1�`��k3/2k�@=2�~�i3�~6�|3�~2+1�j��26�E�E�E�E�E��
��4�@��3�Ԏ��Ɠ��l�ɕ\������Ǝ��̂悤�ɂȂ�܂��B
��k=1�`��k4/2k�@= a(14-0)+a(24-1)�E1/2+ a(34-24)�E1/22+ a(44-34)�E1/23+ a(54-44)�E1/24+�E�E�E�E
������n4-(n-1)4�͖�3�Ɠ��l��
4n3-6n2+4n-1
�����
��k=1�`��k4/2k�@=4��k=1�`��k3/2k-1�|6��k=1�`��k2/2k-1+4��k=1�`��k/2k-1�|��k=1�`��1/2k-1
��k=1�`��k3/2k=26�E�E�E��3���
��k=1�`��k2/2k=6�E�E�E��2���
��k=1�`��k/2k=2�E�E�E��1���
��k=1�`��1/2k=1�E�E�E�������
��k=1�`��k4/2k�@=2�~�i4�~26�|6�~6+4�~2�|1�j��150�E�E�E�E�E��
------------------------------------------------------------
�Ƃ肠����1��ڂ̉������Ē����܂�
�Ԃɍ�����
��k=1�`��kn/2k
�����
��k=1�`��kn/mk
���l���Ă݂����Ǝv���܂�
------------------------------------------------------------
