�����Q�V�N�P�Q���Q�O��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��328�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF11��22���`12��20����
�m���ˉe�̖ʐ��n
�@�F����A�ߋ��̑�w�������̉���ł��B
���P�F���ʁF���Q�{���Q�{���Q���S�E�E�E�@
�@�@�@�@���ʁF�Q���|�Q���{�����R�E�E�E�A�@�@������B
���̂Ƃ��A���ʇ@�ƕ��ʇA�̌����̐}�`�b��xy���ʂɐ��ˉe���Ăł���}�`�c�̖ʐς����߂�B
���Q�F��������ԓ��ŁA�W�̓_
�@�@�@�@�i�O�C�O�C�O�j�A�i���A�O�C�O�j�A�i�O�C���A�O�j�A�i�O�C�O�C���j
�@�@�@�@�i���C���A�O�j�A�i���A�O�A���j�A�i�O�A���A���j�A�i���A���A���j�@�@�i�������A���A���A���͐��̒萔�Ƃ���j
�@�@�@�@�@�_�Ƃ��钼���̂��@�Ƃ��A���ʁ@���{���{�����O�@���A�Ƃ���B
�@���̂Ƃ��A�����̇@�ʇA�ɐ��ˉe���Ăł���}�`�c�̖ʐς����߂�B
NO1�uuchinyan�v
11/22 13��12���@��M �X�V 12/20
��R�Q�W�w�I�ȉ�����
�m���ˉe�̖ʐρn
��ʂɁC��̕��� P�CQ �������āC�����̂Ȃ��p�x���Ƃ̏ꍇ�C
P ��̐}�` C �̖ʐς� S �̂Ƃ��C���̐}�` C �� Q �ւ̐��ˉe���l����ƁC
P�CQ �̌���ɕ��s�ȕ����̒����͕ς�炸�C����ɐ����ȕ����̒����͈ꗥ�� cos�� �{�ɂȂ�̂ŁC
C �� Q �ɐ��ˉe�����}�`�̖ʐ� = S * cos�ƁC
�ɂȂ�܂��B�ȉ��ł́C���̂��Ƃ��g���܂��B
���P�F
���ʁFx^2 + y^2 + z^2 = 4�C���S�����_ (0,0,0) �C���� 2�C�̋��ʁC
���ʁF2x - 2y + z = 3�C���_ (0,0,0) ����̋����� |-3|/��(2^2 + (-2)^2 + 1^2) = 1 �̕��ʁC
�Ȃ̂ŁCO ���畽�ʂɉ����������̑��� H �Ƃ���COH = 1�C�ŁC�Ώ̐����C
�����̐}�` C �́C���S�� H�C���a�� ��(2^2 - 1^2) = ��3�C�̉~�ŁC�ʐς� 3�C�ł��B
����ɁC���̕��ʂ� xy���� �Ƃ̂Ȃ��p�x���ƂƂ���ƁC
���̕��ʂ̖@���x�N�g�� = (2,-2,1)�Cxy���ʂ̖@���x�N�g�� = (0,0,1)�C���C���ς��l���āC
��(2^2 + (-2)^2 + 1^2) * ��(0^2 + 0^2 + 1^2) * cos�� = 2 * 0 + (-2) * 0
+ 1 * 1�C
3 * 1 *
cos�� = 1�Ccos�� = 1/3�C
�����ŁC�ŏ��Ɏ��������Ƃ��C�}�`D �̖ʐ� = 3�� * 1/3 = �C�ɂȂ�܂��B
���Q�F
�}�`D �́C���̂悤�ɍl����C�`��͖��炩�ł��傤�B
�܂��Cxy���ʏ�ɂ��钷���`�� x + y + z = 1 �ɐ��ˉe���C
���ɁCxy���ʏ�̒����`�� z ������ c �������s�ړ����������`�� x + y + z = 1 �ɐ��ˉe����C
���̂Ƃ��Ca�Cb�Cc �̒l�ɂ���̐��ˉe�̓Y���Ă͂ݏo�� D �̌`��͕ω����܂����C
���X�����̂Ƃ��ĂȂ����Ă���̂ŁC�S�̂Ƃ��ĘZ�p�`�ɂȂ�C�͂ݏo���������͒����ׂ̗̂荇�����ʂ̐��ˉe�ł��B
�܂�CD �́C�����̂̈�̒��_�ŗׂ荇���O�̖ʂ𐳎ˉe�����Z�p�`�C�ɂȂ�܂��B
�����ŁC���� x + y + z = 1 �ƁCxy���ʁCyz���ʁCzx���ʁC�Ƃ̂Ȃ��p�x���C���C���C���C�Ƃ���ƁC
�@���x�N�g���Ɠ��ς��l���āC
��(1^2 + 1^2 + 1^2) * ��(0^2 + 0^2 + 1^2) * cos�� = 1 * 0 + 1 * 0 + 1
* 1�Ccos�� = 1/��3�C
��(1^2 + 1^2 + 1^2) * ��(1^2 + 0^2 + 0^2) * cos�� = 1 * 1 + 1 * 0 + 1
* 0�Ccos�� = 1/��3�C
��(1^2 + 1^2 + 1^2) * ��(0^2 + 1^2 + 0^2) * cos�� = 1 * 0 + 1 * 1 + 1
* 0�Ccos�� = 1/��3�C
�����ŁC�ŏ��Ɏ��������Ƃ��C�}�`D �̖ʐ� = (ab + bc + ca)/��3�C�ɂȂ�܂��B
(���z)
���Q�F�� ���� x + y + z = 1 ��ɍ��W������
�}�`D �̌`��ׂ�̂��ʔ��������m��܂���B
����C���P�F�� �}�`D �́C���炩�ɁC�Z�a 1/��3�C���a ��3�C�̑ȉ~�C�ł��ˁB
���Ȃ݂ɁC���Q�F�ŗ����̂̏ꍇ�͂��������m���Ă���C���Z�p�`�ŁC(��3)a^2�C�ł��ˁB
NO2�u�l�c�����v
11/24 18��00���@��M �X�V 12/20
���P
�@�@���Q�{���Q�{���Q���S�E�E�E(1)
�@�@�Q���|�Q���{�����R�E�E�E(2)
�@(1)�C(2)���炚����������ƁC
�@�@���Q�{���Q�{(�R�|�Q���{�Q��)�Q���S
�@�@�����Q�{���Q�{�X�{�S���Q�{�S���Q�|�P�Q���|�W�����{�P�Q�����S
�@�@���T���Q�{�T���Q�|�W�����|�P�Q���{�P�Q���{�T���O�E�E�E(3)
�@�_(���C��)�����_�𒆐S�ɃƉ�]���ē_(�w�C�x)�ɂȂ�Ƃ���ƁC
�@�@�w����cos�Ɓ|��sin�ƁC�x����sin�Ɓ{��cos��
�@�@�������wcos�Ɓ{�xsin�ƁC�����|�wsin�Ɓ{�xcos��
�@(3)�ɑ������ƁC
�@�@�T(�wcos�Ɓ{�xsin��)�Q�{�T(�|�wsin�Ɓ{�xcos��)�Q�|�W(�wcos�Ɓ{�xsin��)(�|�wsin�Ɓ{�xcos��)
�@�@�@�@�|�P�Q(�wcos�Ɓ{�xsin��)�{�P�Q(�|�wsin�Ɓ{�xcos��)�{�T���O�E�E�E(4)
�@�w�x�̍��̌W���́C
�@�@�P�Osin��cos�Ɓ|�P�Osin��cos�Ɓ|�W(cos�Q�Ɓ|sin�Q��)���|�Wcos�Q��
�@�̂ɃƁ��^�S�̂Ƃ��C�w�x�̌W���͂O�ƂȂ�D
�@���̂Ƃ��C(4)����C
�@�@�T{(�w�{�x)�^��Q}�Q�{�T{(�|�w�{�x)�^��Q}�Q�|�W(�w�{�x)�^��Q�E(�|�w�{�x)�^��Q
�@�@�@�@�|�P�Q(�w�{�x)�^��Q�{�P�Q(�|�w�{�x)�^��Q�{�T���O
�@�@���T(�w�Q�{�x�Q)�|�S(�x�Q�|�w�Q)�|�P�Q��Q�E�w�{�T���O
�@�@���X�w�Q�{�x�Q�|�P�Q��Q�E���{�T���O
�@�@���X(�w�Q�|�S��Q�^�R�E���{�W�^�X)�{�x�Q���W�|�T
�@�@���X(�w�|�Q��Q�^�R)�Q�{�x�Q���R
�@�@��(�w�|�Q��Q�^�R)�Q�^(�P�^�R)�{�x�Q�^�R���P
�@�̂�(3)����]����ƁC���̑ȉ~�ɂȂ�D
�@��]�Ŗʐς͕ς��Ȃ��̂ŁC���߂�ʐςr�́C
�@�@�r���E�P�^��R�E��R���E�E�E�i���j
���Q
�@�n(�O�C�O�C�O)�C�`(���C�O�C�O)�C�a(���C���C�O)�C�b(�O�C���C�O)�C�c(�O�C�O�C��)�C�d(���C�O�C��)�C�e(���C���C��)�C
�f(�O�C���C��)�Ƃ���D
�@�n�͕��ʂ��{���{�����O��ɂ���̂ŁC�n�͂n�ɐ��ˉe�����D
�@�`�`�f�����ʂ��{���{�����O�ɐ��ˉe�����_�����ꂼ��`'�`�f'�Ƃ���D
�@���ʂ��{���{�����O�̖@���x�N�g����(�P�C�P�C�P)�Ȃ̂ŁC�����`�`'�̕������́C
�@�@(���|��)�^�P��(���|�O)�^�P��(���|�O)�^�P
�@�@�����|����������
�@���|���������������Ƃ���ƁC
�@�@�������{���C�������C������
�@�_(���{���C���C��)���C���ʂ��{���{�����O��̓_�`'�Ƃ���ƁC
�@�@(���{��)�{���{�����O
�@�@�������|���^�R
�@�@���`'((�Q��)�^�R�C�|���^�R�C�|���^�R)
�@���l�ɁC
�@�@�b'(�|���^�R�C(�Q��)�^�R�C�|���^�R)�C�c'(�|���^�R�C�|���^�R�C(�Q��)�^�R)
�@�����a�a'�̕������́C
�@�@(���|��)�^�P��(���|��)�^�P�����^�P
�@�@�����|�������|������
�@���|�������|�����������Ƃ���ƁC
�@�@�������{���C�������{���C������
�@�_(���{���C���{���C��)�����ʂ��{���{�����O��̓_�a'�Ƃ���ƁC
�@�@(���{��)�{(���{��)�{�����O
�@�@������(�|���|��)�^�R
�@�@���a'((�Q���|��)�^�R�C(�|���{�Q��)�^�R�C(�|���|��)�^�R)
�@���l�ɁC
�@�@�d'((�Q���|��)�^�R�C(�|���|��)�^�R�C(�|���{�Q��)�^�R)
�@�@�f'((�|���|��)�^�R�C(�Q���|��)�^�R�C(�|���{�Q��)�^�R)
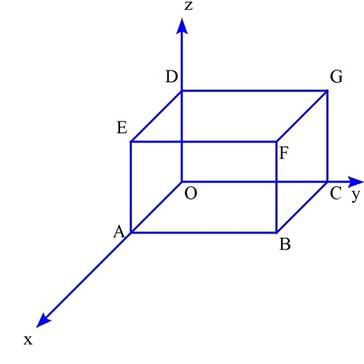
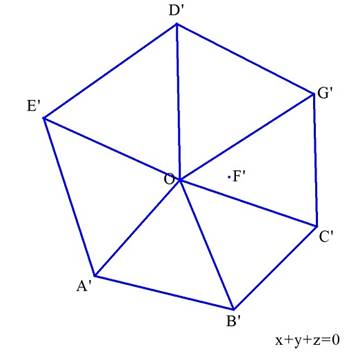
�@�}���C
�@�@�Z�p�`�`'�a'�b'�f'�c'�d'�����n�`'�a'�{���n�a'�b'�{���n�b'�f'�{���n�f'�c'�{���n�c'�d'�{���n�d'�`'
�̖ʐς����߂�悢�D
�@���n�`'�a'�ɂ����āC
�@�@�n�`'�Q���S�^�X�E���Q�{���Q�^�X�{���Q�^�X���Q�^�R�E���Q
�@�@���n�`'����Q�^��R�E��
�@�܂��C
�@�@�`'�a'�Q�����Q�^�X�{�S�^�X�E���Q�{���Q�^�X���Q�^�R�E���Q
�@�@���`'�a'����Q�^��R�E��
�@���ɁC
�@�@�n'�a'�Q��(�Q���|��)�Q�^�X�{(�|���{�Q��)�Q�^�X�{(�|���|��)�Q�^�X���Q�^�R�E(���Q�|�����{���Q)
�@�@���n'�a'����Q�^��R�E(���Q�|�����{���Q)�P�^�Q
�@�n�`'�F�`'�a'�F�n'�a'�����F���F(���Q�|�����{���Q)�P�^�Q�Ȃ̂ŁC
�@�@cos�ڂn�`'�a'��{���Q�{���Q�|(���Q�|�����{���Q)}�^(�Q����)���P�^�Q
�@�@��sin�ڂn�`'�a'����R�^�Q
�@�@�����n�`'�a'���P�^�Q�E�n�`'�E�`'�a'�Esin�ڂn�`'�a'
�@�@�@�@�@�@�@�@���P�^�Q�E(��Q�^��R�E��)�E(��Q�^��R�E��)�E��R�^�Q��(����)�^(�Q��R)
�@���n�a'�b'�ɂ����āC
�@�@�n�a'����Q�^��R�E(���Q�|�����{���Q)�P�^�Q�C�a'�b'����Q�^��R�E���C�n�b'����Q�^��R�E��
�@�@�����n�a'�b'��(����)�^(�Q��R)
�@���n�b'�f'�ɂ����āC
�@�@�n�b'����Q�^��R�E���C�b'�f'����Q�^��R�E���C�n�f'����Q�^��R�E(���Q�|�����{���Q)�P�^�Q
�@�@�����n�b'�f'��(����)�^(�Q��R)
�@���n�f'�c'�ɂ����āC
�@�@�n�f'����Q�^��R�E(���Q�|�����{���Q)�P�^�Q�C�f'�c'����Q�^��R�E���C�n�c'����Q�^��R�E��
�@�@�����n�f'�c'��(����)�^(�Q��R)
�@���n�c'�d'�ɂ����āC
�@�@�n�c'����Q�^��R�E���C�c'�d'����Q�^��R�E���C�n�d'����Q�^��R�E(���Q�|�����{���Q)�P�^�Q
�@�@�����n�c'�d'��(����)�^(�Q��R)
�@���n�d'�`'�ɂ����āC
�@�@�n�d'����Q�^��R�E(���Q�|�����{���Q)�P�^�Q�C�d'�`'����Q�^��R�E���C�n�`'����Q�^��R�E��
�@�@�����n�d'�`'��(����)�^(�Q��R)
�@�̂ɖʐς́C
�@�@(�����{�����{����)�^��R����R�^�R�E(�����{�����{����)
NO3�u�ɂ���Z12�v 11/28 01��47���@��M
�X�V 12/20
���P�F���ʁF���Q�{���Q�{���Q���S�E�E�E�@
�@�@�@�@���ʁF�Q���|�Q���{�����R�E�E�E�A�@�@������B
���̂Ƃ��A���ʇ@�ƕ��ʇA�̌����̐}�`�b��xy���ʂɐ��ˉe���Ăł���}�`�c�̖ʐς����߂�
���ʂʂŐ�i��_�̏W���j�Ɖ~�ɂȂ邩�A�����Ȃ����A�_�Ō���邩��3�ʂ肪����܂��B
���̂����A�~�ƂȂ�ꍇ�����ʐς������Ȃ��̂ŁAC�͉~�ƂȂ�ƍl���܂��B
���̎��A�������ʂւ̐��ˉe�̖ʐς́AC�ƁA�A��xy���ʂ��ׂ��p�x�̗]�����|�����l�ƂȂ�܂��B
�܂��A�@�̋��͒��S�����_O�Ɏ����A���a��2�ł��B
����ɉ~C�̒��S��O�f�Ƃ���ƁA����OO�f�͕��ʇA�ƒ������܂��i���̂��Ƃ͐��ʂɕ����ԋ����l����ƃC���[�W�ł��܂��j
�悸C�����߁A�p�x�����߂��̗]����������Ƃ������j�ʼn����Ă݂܂��B
���A���A���̊e���ƕ��ʇA�̌������W�͊e�Xy=z=0,x=z=0,x=y=0���A�ɑ�������
(3/2,0,0),(0,-3/2,0),(0,0,3)�ƂȂ�܂��B�i������A�_E,F,G�Ƃ��܂��j
�����ŕ��ʂ�+����0���l����ƕ��ʇA�y�т������ʂɑ��_E,F,G�̈ʒu���琂�ʂƂȂ�܂��B
�܂���L3���ʂ̌�_��EF�̒��_�ƂȂ�̂�(3/4,-3/4,0)�ƂȂ肱�̓_��P�Ƃ��܂�
���ʇA�Ƃ������ʂƂ̂Ȃ��p�x�̗]����cos��GPO�Ȃ̂�
(3��2/4)�^��((3��2/4))2+32)=1/3
O�f�̍��W�͒���OO�f�����ʇA�ƒ������邱�Ƃ���
����3/4�E�i1-1/32�j��2/3
����-����-2/3
����3�E�i1/3�j�E�i1/3�j��1/3
�i2/3,-2/3,1/3�j
�ƂȂ�܂��B
�܂����_����̒�����
OO�f=��((2/3)2+(-2/3)2+(1/3)2) =1
�����
�~C�́A���ʂ�+����0�Ƃ���_�������Ƃ�O�f���̕��ʏ�ɂ��邱�Ƃ��疾�炩�ł��B
�����Ň@�A�A�ƘA�����ĉ�����
����(4�}��6)/6
����-(4�}��6)/6
����-(-1�}2��6)/3
���_����̒�����
��(((4+��6)/6)2+(-(4+��6)/6)2+(-(-1+2��6)/3)2)=
��(((4-��6)/6)2+(-(4-��6)/6)2+(-(-1-2��6)/3)2)=2
�~C�̔��a��
��i22-12�j����3
�ʐς�
��(��3)2=3��
xy���ʂɐ��ˉe���Ăł���}�`�c�̖ʐς�
�������ʂƂ̂Ȃ��p�x�̗]��1/3��������
D=3�E1/3���E�E�E�E��
�ʉ�
���A���A���̊e���ƕ��ʇA�̌������W�͊e�Xy=z=0,x=z=0,x=y=0���A�ɑ�������
(3/2,0,0),(0,-3/2,0),(0,0,3)�ƂȂ�܂��B�i������A�_E,F,G�Ƃ��܂��j
�����ŕ��ʂ�+����0���l����ƕ��ʇA�y�т������ʂɑ��_E,F,G�̈ʒu���琂�ʂƂȂ�܂��B
�܂���L3���ʂ̌�_��EF�̒��_�ƂȂ�̂�(3/4,-3/4,0)�ƂȂ肱�̓_��P�Ƃ��܂�
���ʇA�Ƃ������ʂƂ̂Ȃ��p�x�̗]����cos��GPO�Ȃ̂�
(3��2/4)�^��((3��2/4))2+32)=1/3
�܂�O�f�̌��_����̒�����G�̂����W��cos��GPO��cos��GOO�f��������
OO�f=3�E�i1/3�j=1
�����
�~C�́A���ʇ@�Ƃ̌���ł��邱�Ƃ���
���_����̒����͇@�̔��a�ɓ�����
2
�~C�̔��a��
��i22-12�j����3
�ʐς�
��(��3)2=3��
xy���ʂɐ��ˉe���Ăł���}�`�c�̖ʐς�
�������ʂƂ̂Ȃ��p�x�̗]��1/3��������
D=3�E1/3���E�E�E�E��
���Q�F��������ԓ��ŁA�W�̓_
�@�@�@�@�i�O�C�O�C�O�j�A�i���A�O�C�O�j�A�i�O�C���A�O�j�A�i�O�C�O�C���j
�@�@�@�@�i���C���A�O�j�A�i���A�O�A���j�A�i�O�A���A���j�A�i���A���A���j�@�@�i�������A���A���A���͐��̒萔�Ƃ���j
�@�@�@�@�@�_�Ƃ��钼���̂��@�Ƃ��A���ʁ@���{���{�����O�@���A�Ƃ���B
�@���̂Ƃ��A�����̇@�ʇA�ɐ��ˉe���Ăł���}�`�c�̖ʐς����߂�B
�W�̓_�i�O�C�O�C�O�j�A�i���A�O�C�O�j�A�i�O�C���A�O�j�A�i�O�C�O�C���j
�@�i���C���A�O�j�A�i���A�O�A���j�A�i�O�A���A���j�A�i���A���A���j
���AO�i���_�jA,B,C,D,E,F,G�Ƃ��܂�
����x=y=z�͕��ʇA�ɉ����ƂȂ�̂ŇA�ɐ��ˉe���������_O�Ɉ�v���܂��B���̒������B�Ƃ��܂��B
x,y,z�e���𐳎ˉe�������݂̌��ɂȂ��p�x�͓������̂�120���E�E�E�E�E�C
�B��x,y,z�e���̂Ȃ��p�x�̗]���́A�P/��3�Ȃ̂Ŋe�������ʇA�ƂȂ��p�x�̗]���́�(2/3)�ƂȂ�܂��B
���������āA�e���ɕ��s�Ȓ����̇A�ւ̐��ˉe�̒����͂��ׂā�(2/3)���悶���l�ƂȂ�܂��B�E�E�E�D
�܂��A�e���Ƃ̕��s�Ȓ����͇A�ɐ��ˉe���Ă����s�ł��B������E
�C�D�E���琳�ˉe���Ăł���}�`�c��
ADBFCE�̂U�p�`��
CE�ABD�AOA�ix���j�͕��s�Œ����́�(2/3)�Ea
CF�AAD�AOB�iy���j�͕��s�Œ����́�(2/3)�Eb
AE�ABF�AOC�iz���j�͕��s�Œ����́�(2/3)�Ec
(��OC,OA,OB,GD,GF,GE���c�̓����ɂȂ�܂�)
�ʐς�
OADO,BFCB,OCEA�̊e�����`�𐳎ˉe�������̘a�ɓ������̂�
(ab+bc+ac)�sin60���(��(2/3))2����3 /3(ab+bc+ac)�@�@�@�@�@�@�E�E�E�E��
���z�F���1�͕ʉ���{���Ƃ����������̂ł����A�����ɂ���������������Ă��炤���߂ɍڂ��܂����B
�@�@�@���́A�ʉ��͕z�c�̒��ōl�������̂ŁA���Ɍ������Ă�������ڂ��Ԃ��ē��̒������ōl���Ă���Ƃ��̕����N���A�Ȃ��Ƃ�����悤�ł��B
�@�@�@�{���ŁA�����Ă�����ƂĂ��ł͊Ԃɍ����܂���B�ʉ��Ȃ�10�����x�ʼnł���Ǝv���܂��B
�@�@�@���2�ɂ��ẮA�u����x=y=z�͕��ʇA�ɉ����ƂȂ�v���Ƃ��x�N�g���̓��ς������ŏؖ����ׂ��Ƃ��납������܂������ł킩��̂Ŋ������܂����B
�@�@�@�C�͇A���Ώ̎��Ȃ̂Ŗ��炩���Ǝv���܂��B
�@�@�@�D�͇B�̔C�ӂ̓_Q����e���ɐ����̑����������Ƃ��̓_��J�Ƃ����_�Ƃł���O�p�`��QJO
�@�@�@J����A�ɐ����̑����������Ƃ��̓_��K�Ƃ����_�Ƃł���O�p�`��JKO
�@�@�@JK��QO�ƕ��s�ł��邱�Ƃ��灢QJO�䁢OKJ�AQ���i1,1,1�j�Ƃ����OQ=��3�AJQ=��2���瓱���܂����B
�@�@�@�ǂ���̖����������V���v���Ȃ̂ʼn��Ƃ��Ȃ�܂������A���1�A2�Ƃ��A�̂��Ƃ��̌W�����قȂ��Ă����肵�Ă��邾���œ�����������ł��B
�u�ɂ���Z12�v 12/03 01��01���@��M
�X�V 12/20
�����̗���F�u�~C�̔��a�����߂�̂ɂ͋��ʂ̒��S�̌��_���畽�ʇA�܂ł̋��������߂����������܂�����v��
���́A���̌������w���Ƃ͊o���Ă��܂����B
�ł��w���Ƃ��o���Ă����ɂ������A�������͖̂Y��Ă��܂��Ă��܂��B
�o���邾���A�u���v�̎����̗͂������������Ǝv���Ă���̂�
��蕶�����Ă���͂ق��̎Q�l���i�T�C�g���܂߁j���Ȃ��ʼn������Ƃ�S�����Ă��܂��B
�i���X�ǂ����悤���Ȃ��Y�����Ă��܂����Ƃ͂���܂��i�Q������A���������w������ɂ�������Ƃ��Ȃ������̂Łj���E�E�E�j
�������A���M���Ă���͍ēx���낢��ȃT�C�g��Q�l���ŕ��K���܂��B�i���ꂪ�y���݂ł������ł��āc�j
����Ȃ킯�ŁA���_���畽�ʇA�܂ł̋��������߂�������u���̎����v�ŗU�����Ă݂悤�Ǝv���܂��B
�Q���|�Q���{�����R�E�E�E�A
�A�̊e�W���Ə퐔��a,b,c,d�A���_����̋�����D�Ƃ��A��ʉ����܂��B
a��+b���{c����d�E�E�E�A
�����ŁAd=0�̏ꍇ���_��ʂ�̂�D=0
������a,b,c,d��0�łȂ������Ƃ��܂��B
����ɁA�W�������Ȃ����邽�ߗ��ӂ�a�Ŋ���
B=b/a,C=c/a,D=d/a�ƒu����
��+B���{C����D�E�E�E�A�f
���_�𒆐S�Ƃ��鋅�ʂ�
��2+��2+��2����2�E�E�E(�)
�A�f��(�)���ڂ���Ƃ����̐ړ_P�ƌ��_�����Ԑ����͇A�f�ɐ����Ȃ̂�OP�͌��_����A�f�܂ł̋����ƂȂ�܂��B
�܂��A���̎��A�f��(�)�̘A���������͂�����̏d���������܂�
�A�f��
����D-B��-C��
�ƕό`��(�)�ɑ�������Ƃ��ɂ��ĉ����A�����̒���0�i�d���j�Ƃ����
��=B(D-Cz)/(B2+1)
z=C(D-Bz)/(C2+1)
�����
��=BD/(B2+C2+1)
z=CD/(B2+C2+1)
�A�f�ɑ�����Ă��ɂ��ĉ�����
����CD/(B2+C2+1)
����ɏ�Lx�y�z��(�)�ɑ�������i���̎����j�����߂��
����D/��(B2+C2+1)
B=b/a,C=c/a,D=d/a���������ɖ߂���
����d/��(a2+b2+C2)�E�E�E�E�E�E�E�E����
P�̍��W��
x����ad/( b2+ c2+
a 2)
y����bd/( b2+ c2+
a 2)
z����cd/( b2+ c2+
a 2)
O,P��ʂ钼����xy�Ayz�̊e���ʂւ̐��ˉe�͑��X
y��y��x/x����bx/a
z��z��y/y����cy/b
�����O,P��ʂ钼���̕�������
x/a��y/b��z/c�E�E�E�E�E�E�E�E����
O,P��ʂ钼����xy���ʂƂȂ��p�x���ƂƂ����
|tan��|��|z��|/��(x��2+y��2)��|c|/��(a2+b2)
|sin��|��|z��|/��(x��2+y��2+ z��2)��|c|/��(a2+b2+c2)
|cos��|����(x��2+y��2)/��(x��2+y��2+ z��2)����(a2+b2)/��(a2+b2+c2)
���ʇA��xy���ʂƂȂ��p�x���̓�/2-�ƂȂ̂�
|tan(��/2-��) |��|cot��|����(x��2+y��2) /| z��|����(a2+b2)/ |c|
|sin(��/2-��) |��|cos��|����(x��2+y��2)/��(x��2+y��2+ z��2)����(a2+b2)/��(a2+b2+c2)
|cos��|��|cos(��/2-��) |��|sin��|��|z��|/��(x��2+y��2+ z��2)��|c|/��(a2+b2+c2)
���l�ɕ��ʇA��yz���ʂƂȂ��p�x�����Axz���ʂƂȂ��p�x�����Ƃ����
|cos��|��|x��|/��(x��2+y��2+ z��2)��|a|/��(a2+b2+c2)
|cos��|��|y��|/��(x��2+y��2+ z��2)��|b|/��(a2+b2+c2)
�����̗]���̐�Βl�́A�A���ʂ�xy,yz,zx���ʂւ�OP�����̒����̎ʑ��ł��B�܂��Axy,yz,zx���ʂ̇A���ʂւ�OP�����̒����̎ʑ��ł�����܂��B
���o����������p���āA���1�A2�̕ʉ������߂Ă݂܂�
�Q���|�Q���{�����R�E�E�E�A
���1�ʉ�����2
���ʂ���Ɖ~C�ƂȂ�A���̒��S�����_O�A�ؒf�ʂ̉~C�̒��S��O�f�Ƃ����
O�f�͋��̒��S�ł��錴�_��ʂ�A���ʇA�ɐ����Ɍ���钼���ƕ��ʇA�Ƃ̌�_�ƂȂ�܂��B
���̒��S�ł��錴�_��ʂ�A���ʇA�ɐ����Ɍ���钼���̕�������
��/2��-��/2����
OO�f=3/��(22+(-2)2+12)=1
�܂��A�~C�̉~���͋��Ƃ̌���ł��邱�Ƃ��猴�_����̒����͇@�̔��a�ɓ�����
OC��2
����ĉ~C�̔��a��
��i22-12�j����3
�ʐς�
��(��3)2=3��
�~C��xy���ʂւ̐��ˉe�̖ʐς͕��ʇA��xy���ʂƂ̂Ȃ��p�x���̗]���̐�Βl�ɉ~�̖ʐς��悶�����̂ƂȂ�܂�
cos����1/��(22+(-2)2+12)=1/3
�����xy���ʂɐ��ˉe���Ăł���}�`�c�̖ʐς�
D=3�E1/3���E�E�E�E��
���2�ʉ�
�W�̓_�i�O�C�O�C�O�j�A�i���A�O�C�O�j�A�i�O�C���A�O�j�A�i�O�C�O�C���j
�@�i���C���A�O�j�A�i���A�O�A���j�A�i�O�A���A���j�A�i���A���A���j
���AO�i���_�jA,B,C,D,E,F,G�Ƃ��܂�
���ʇA��xy,yz,zx�e���ʂ̂Ȃ��p�x�̗]���̐�Βl�͕��ʇA�̕������̊e�W����1�Ȃ̂ł��ׂ�
|1|/��(12+12+12)����3 /3
���ˉe���Ăł���}�`�c��
ADBFCE�̂U�p�`��
(��OC,OA,OB,GD,GF,GE���c�̓����ɂȂ�܂�)
�ʐς�
OADO,BFCB,OCEA�̊e�����`���A�ɐ��ˉe�������̘a�ɓ������̂�
��3 /3(ab+bc+ac)�@�@�@�@�@�@�E�E�E�E��
NO4�u���N���̂�������v 11/29 16��07���@��M �X�V 12/20
���1
�����@�ƕ����A�̌����̐}�`C�͉~�ł��B
![]()
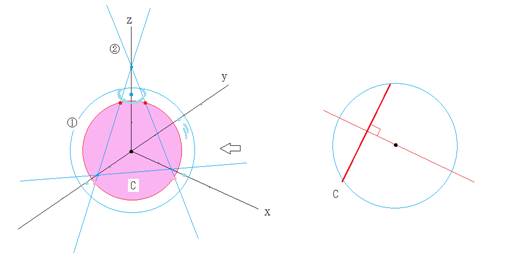
�E�́A����������݂��Ƃ��̗l�q�ł��B
���_���炱�̒����܂ł̋���d�́A![]() �ł��B
�ł��B
���̔��a��2�Ȃ̂ŁA�~C�̔��a�� ![]() �ƂȂ�A�~�̖ʐς�
�ƂȂ�A�~�̖ʐς�![]() �ł��B
�ł��B
�����A�̖@���x�N�g���́A�ϐ��̌W��(2, �|2, 1)�ł��B
���_��ʂ蕽���A�ɐ����Ȓ����B�́A���̃x�N�g��������x�N�g���Ƃ��āA![]() �ł��B
�ł��B
�����A�ƒ����B�Ƃ̌�_H�̍��W�́A
![]() �Ƃ��āA�A�̎��ɑ������ƁA
�Ƃ��āA�A�̎��ɑ������ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA![]() �ł��B
�ł��B
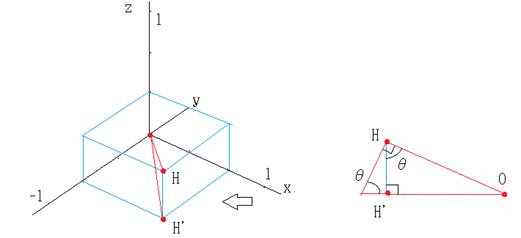
��_H��X-Y���ʂւ̐��ˉe�̓_��H�f�Ƃ��܂��B
�����A��X-Y���ʂ̂Ȃ��p���ƂƂ���ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA![]() �D
�D
�ȏォ��A�}�`C�̋��߂�ʐ�S�́A![]() �ƂȂ�܂��B
�ƂȂ�܂��B
���2
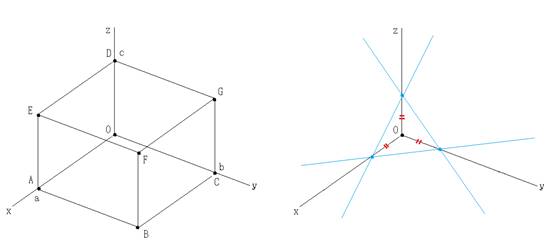
�������@��8�̓_�Ɏ��̂悤�ɖ��O�����܂�
![]()
�����A�ix�{y�{z��0�j�͉E�̐}�̕��ʂɕ��s�Ō��_��ʂ�܂��B
�i�C���[�W���ɂ����̂ł킴�Ə������炵�Ċ��������݂܂��j
�_F��ʂ蕽���A�ɐ����Ȓ����́A![]() �ł��B
�ł��B
���̎��̒l�����Ƃ����āA�����A�Ƃ̌�_�����߂܂��B
![]() ���A�ɑ�����������܂��B
���A�ɑ�����������܂��B
![]() �@
�@![]() ���A
���A
![]() �D
�D
��������ƂɁA�e�_���A�ւ̐��ˉe�̍��W�����߂܂��B
�eA�AB�AC�A������ˉe�����_��P�AQ�AR�A����Ƃ��܂��B
![]() �@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@![]()
![]() �@�@�@�@
�@�@�@�@![]()
![]() �@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@![]()
![]() �@
�@![]()
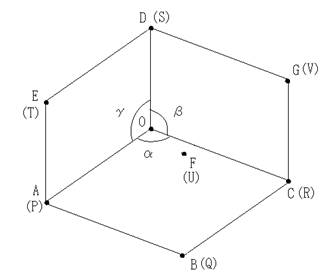
�����ŁA���ˉe���ꂽ�e�_�̋����ׂ܂��B
![]() ���l��
���l��
![]()
![]() ���l��
���l��
![]()
![]() ���l��
���l��
![]()
���̌��ʂ���A��OPQR�A��ORVS�A��OSTP�����s�l�ӌ`�ł��邱�Ƃ�������܂��B
���ɁA�p�̑傫���ׂ܂��B
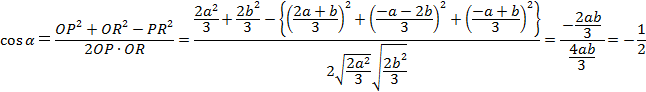
���A����120���B
���l�ɁA��������120���ł��B
����āA�}�`D�̖ʐ�S�́A
![]()
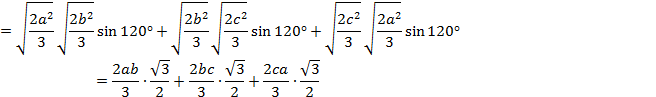
![]()
NO5�u��x�Ђ����v 12/13
11��27���@��M �X�V 12/20
���1: �}�`D�̖ʐς� �� (��)
���_O�ƕ��� 2*x-2*y+z=3 �Ƃ̋�����
|2*0-2*0+1*0-3|/��(2^2+(-2)^2+1^2)=3/3=1
�ł���̂ŁC�^����ꂽ���ƕ��ʂ͌����C
�}�`C�͉~�ƂȂ�D�@
���_O���畽�� 2*x-2*y+z=3�ɉ��낵�������̑���H�Ƃ���D
H�͉~C�̒��S�ƈ�v����D
�܂�C��̈�_��P�Ƃ���D
OP=2�COH=1�D
�����C�̖ʐς� HP^2*��=(OP^2-OH^2)*��=(2^2-1^2)*��=3*�D
xy���ʂ̖@���x�N�g���� a��=(0�C0�C1)�Ƃ��C
����2*x-2*y+z=3�̖@���x�Eu��D���C�w)����u�療���=(2�C-2�C1)�Ƃ���D
n����a���̂Ȃ��p�����Ƃ���ƁC
cos(��)=(n���Ca��)/(|n��|*|a��|)=1/3�D
xy���ʂƕ���2*x-2*y+z=3�̂Ȃ��p����(0���Ɓ���/2)�Ƃ���ƁC
cos(��)=|cos(��)|=1/3�D
���߂�ʐς� (C�̖ʐ�)*cos(��)=(3*��)*(1/3)=�D
���2: �}�`D�̖ʐς� (1/��3)*(a*b+b*c+c*a) (��)
�^����ꂽ8�̓_���C
O(0�C0�C0)�CX(a�C0�C0)�CY(0�Cb�C0)�CZ(0�C0�Cc)�C
E(a�Cb�C0)�CF(a�C0�Cc)�CG(0�Cb�Cc)�CH(a�Cb�Cc)
�Ƃ���D
6�̒����` OXEY�CZFHG�COXFZ�CYEHG�COYGZ�CXEHF
�����ꂼ��CT_1�CT_2�CT_3�CT_4�Cw)�����݁E��u����������Ƃ���D
T_i�� x+y+z=0 �ɐ��ˉe���Ăł���}�`�̖ʐς�
S_i �Ƃ��� (i=1�C2�C3�C4�C5�C6)�D
������OXEYGZFH�͓ʑ��ʑ̂ł���̂ŁC�}�`D�̖ʐς�
(1/2)*(S_1 + S_2 + S_3 + S_4 + S_5 + S_6)
�ŗ^������D
���� x+y+z=0 �̖@���x�N�g���́Cn��=(1�C1�C1)�D
T_1���܂ޕ��ʂ̖@���x�N�g���� p��=(0�C0�C1)�D
n���� p�� �̂Ȃ��p�����Ƃ���ƁC
cos(��)=(n���Cp��)/(|n��|*|p��|)�D
���� x+y+z=0 �� T_1 ���܂ޕ��ʂ̂Ȃ��p����(0���Ɓ���/2)�Ƃ���ƁC
cos(��)=|cos(��)|�D
S_1= (T_1�̖ʐ�)*cos(��)=(a*b)*|(n���Cp��)/(|n��|*|p��|)|
= (a*b)/��3�D
���l�ɁCS_2 = (a*b)/��3�D
T_3���܂ޕ��ʂ̖@���x�N�g���� q��=(0�C1�C0)�D
S_3=(c*a)*|(n���Cq��)/(|n��|*|q��|)| = (c*a)/��3�D
���l�ɁCS_4 = (a*c)/��3�D
T_5���܂ޕ��ʂ̖@���x�N�g���� r��=(1�C0�C0)�D
S_ 5=(b*c)* |(n���Cr��)/(|n��|*|r��|)| = (b*c)/��3�D
���l�ɁCS_6 = (b*c)/��3�D
(�}�`D�̖ʐ�)
=(1/2)*(S_1 + S_2 + S_3 + S_4 + S_5 + S_6)
=(1/2)*(2*(a*b)/��3 + 2*(c*a)/��3
+ 2*(b*c)/��3)
=(1/��3)*(a*b+b*c+c*a)�D
���@���2�ł́C
�u�ʑ��ʑ̂ʂɐ��ˉe���Ăł���}�`
�̖ʐς�2�{�́C���̓ʑ��ʑ̂̊e�ʂ𐳎ˉe���Ăł���
�}�`�̖ʐς̘a�ɓ������v
�Ƃ����������g���ĉ����̂ł����C���̎�����
���������ǂ��������ؖ��ł����ł��傤���H
�����̗���F������܂���B�ǂȂ��������Ă��������B��
�Ԏ��u�ɂ���Z12�v 12/25 04��05���@��M
�X�V 12/26
�u��x�Ђ����v����N����Ă����ۑ�ł��B
�@���̉ł��A�u��OC,OA,OB,GD,GF,GE���c�̓����ɂȂ�܂��v�Ɖ��̐������Ȃ��ɏq�ׂĂ���̂ŏؖ����Ă����K�v������܂����B
���@���2�ł́C
�u�ʑ��ʑ̂ʂɐ��ˉe���Ăł���}�`
�̖ʐς�2�{�́C���̓ʑ��ʑ̂̊e�ʂ𐳎ˉe���Ăł���
�}�`�̖ʐς̘a�ɓ������v
�Ƃ����������g���ĉ����̂ł����C���̎�����
���������ǂ��������ؖ��ł����ł��傤���H
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1.�@���Ɠ����ȂR�������ʑ�D��A�ɐ��ˉe���������̑��p�`��s�ʐς�S�Ƃ���B���̎��X�㕽��A�����ɂ����܂�
1.�@���Ɠ����ȂR�������ʑ�D��A�ɐ��ˉe���������̑��p�`��s�ʐς�S�Ƃ���B���̎��X�㕽��A�����ɂ����܂�
�@�@A�ƕ��s�ȕ���B���l���}�̂悤�ɉE�ɂ����܂��BD��B�ɐ��ˉe���������̑��p�`s�f�ʐς�S�f�Ƃ��܂��B
�@�@���̎��A���炩��s��s�f�͍����ł�
2.�@�ʌ^���ʑ̂��\�����邷�ׂĂ̕�(�Q�ʊp)��180������(�Ő�)�ł�
3.�@A��D�̍����̑��p�`�Q�AB�ɂ�D�̍����̑��p�`�Q���ˉe�����ƍl���܂��B
4.�@2����AA�AB�ɂ̗����Ɏˉe����鑽�p�`��A,B�̐��ʂŎˉe�ʐς�0
5.�@2����AD���\�����鑽�p�`��A,B�Ɏˉe�����Ƃ��e�ʂɂ����ďd�Ȃ邱�Ƃ͂Ȃ��B
6.�@4,5����D���\�����鑽�p�`��A,B�̂����ꂩ�ɂ��ׂďd�Ȃ�Ȃ��Ŏˉe�����
7.�@6����A�ʌ^���ʑ̂��\�����邷�ׂĂ̑��p�`��A,B�ւ̐��ˉe�̖ʐς�S+S�f
8.�@ s��s�f�͍����Ȃ̂�6����S=S�f����āA�ʌ^���ʑ̂��\�����邷�ׂĂ̑��p�`�̐��ˉe�̖ʐς�D��A�ւ̐��ˉe�̖ʐς̂Q�{�ɓ������B
9.�@�X��A�����AB���E�ɂ����܂������AAB��ʂƂ��AD���\�����鑽�p�`��\�Ɨ��ɕ����čl���Ă����l�̌��_�ɂȂ�܂��B
�����悻�A�ؖ��炵���Ȃ��ؖ��ł����A���̂��Ƃ������ɘ_���Ă����A�^�̏ؖ��ɂ��ǂ蒅����̂ł͂Ȃ��ł��傤���B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
