平成２９年４月１６日

[流れ星]

　　　　　第345回数学的な応募解答

　　　　　　＜解答募集期間：３月１９日〜４月１６日＞

［3桁の数字］

　3桁の数字ＡＢＣの桁を並び替えて得られる（ＡＢＣを含めて）６つの数の平均が、ちょうどもとの数ＡＢＣになるような数字について、次の問に答えよ。ただし、問２では百の位に０となったときは2桁の数字とする。

問１：Ａ，Ｂ，Ｃが1から９の相異なる数のとき、このような数字が４つある。すべて求めよ。

問２：Ａ，Ｂ，Ｃが０から９の相異なる数のとき、このような数字があと２つ増える。これらを求めよ。

「出典：数に強くなろう　ピーター・フランクル著　（岩波ジュニア新書）」

NO1「uchinyan」 03/19 15時59分　受信 更新 4/16

問１：

ABC は 100A + 10B + C と書けるので，A，B，C を入れ替えた平均は，

((A + B + C) * 2 * 100 + (A + B + C) * 2 * 10 + (A + B + C) * 2 * 1)/6

= (A + B + C) * 222/6 = 37(A + B + C)，

これがもとの 100A + 10B + C に等しいので，

37(A + B + C) = 100A + 10B + C，63A = 27B + 36C，7A = 3B + 4C，

3(A - B) = 4(C - A)，

A，B，C は 1 〜 9 の相異なる数で，-8 <= A - B <= 8，-8 <= C - A <= 8，で，

3 と 4 は互いに素なので，A - B = 4 の倍数，C - A = 3 の倍数，より，次のとおり。

A - B = -8 の場合，C - A = -6，で，解なし。

A - B = -4 の場合，C - A = -3，で，(A,B,C) = (4,8,1), (5,9,2)。

A - B = +4 の場合，C - A = +3，で，(A,B,C) = (5,1,8), (6,2,9)。

A - B = +8 の場合，C - A = +6，で，解なし。

以上ですべてなので，ABC = 481，518，592，629，になります。

問２：

．．．

3(A - B) = 4(C - A)，までは，問１：と同じ。

A，B，C は 0 〜 9 の相異なる数で，-9 <= A - B <= 9，-9 <= C - A <= 9，で，

3 と 4 は互いに素なので，A - B = 4 の倍数，C - A = 3 の倍数，より，次のとおり。

A - B = -8 の場合，C - A = -6，で，解なし。

A - B = -4 の場合，C - A = -3，で，(A,B,C) = (3,7,0), (4,8,1), (5,9,2)。

A - B = +4 の場合，C - A = +3，で，(A,B,C) = (4,0,7), (5,1,8), (6,2,9)。

A - B = +8 の場合，C - A = +6，で，解なし。

以上ですべてなので，ABC = 370, 407, 481，518，592，629，になります。

増えるのは，370 と 407 ですね。

(考察)

各桁の数字が相異なる限り，使える数字は 0 〜 9 しかないので 11 桁以上はあり得ません。

10 桁以下の n 桁の場合，条件を満たす数を m とし，m の各桁の数字の和を s(m) と書くと，

(s(m) * (n-1)! * 11…11)/n! = m，(s(m) * 11…11)/n = m，

ただし，11…11 は 1 が n 個並んだ数，となります。

そこで，s(m) * 11…11 は n の倍数になりますが，

もし 11…11 と n が互いに素とすると，s(m) が n の倍数になります。

ところが，s(m)/n が２桁以上の場合は，左辺は n 桁を超えるので m に等しいはずがなく，

s(m)/n が１桁の数の場合は，11…11 に掛けると各桁の数字が同じになり「相異なる」に矛盾します。

つまり，11…11 と n が互いに素の場合には解がないことになります。

具体的には，２桁，４桁，５桁，７桁，８桁，10桁，では解がないことになります。

一方で，１桁，３桁，６桁，９桁では解がある可能性があります。

１桁は自明ですが，

３桁では，s(m) * 37 = m，で，上記は確かに解があることを示しています。

６桁の場合は，37037 * s(m)/2 = m，で，

各桁の数字が相異なることと s(m) が偶数とから

s(m) = 16, 18, 20, 22, 24, 26, 30, 32, 34, 36, 38，が候補ですが，

s(m)/2 <= 19，で，19 * 37 = 703，となって，

37037 に掛けても各桁の数字が「相異なる」を実現できません。

つまり，解はないようです。

９桁の場合は，12345679 * s(m) = m，で，

各桁の数字が相異なることから

s(m) = 36, 37, 38, 39, 40, 41, 42, 43, 44, 45，が候補ですが，

s(m) = 36，m = 444444444，不可，

s(m) = 37，m = 456790123，可，

s(m) = 38，m = 469135802，可，

s(m) = 39，m = 481481481，不可，

s(m) = 40，m = 493827160，可，

s(m) = 41，m = 506172839，可，

s(m) = 42，m = 518518518，不可，

s(m) = 43，m = 530864197，可，

s(m) = 44，m = 543209876，可，

s(m) = 45，m = 555555555，不可，

となるようです。

ただし，0 を含まないものは，明らかに，あり得ませんね。

(感想)

これは数学というよりパズルという感じの問題ですね。

考察で他の桁数の場合も調べてみました。

６桁で解がないようなのがちょっと意外でした。本当だろうか。

NO2「早起きのおじさん」 03/20 22時23分　受信 更新 4/16

その1

問1

数字A、B、Cを並び替えてできる6個の数を次に並べます。

　A×100＋B×10＋C、A×100＋C×10＋B

　B×100＋A×10＋C、B×100＋C×10＋A

　C×100＋A×10＋B、C×100＋B×10＋A

これらの6個の数の和は、

　2(A＋B＋C)×100＋2(A＋B＋C)×10＋2(A＋B＋C)

これらの平均が、A×100＋B×10＋Cなので、

　2(A＋B＋C)×100＋2(A＋B＋C)×10＋2(A＋B＋C)＝6×(A×100＋B×10＋C)

整理すると、

　7A＝3B＋4C ･･･ （＊）

あ）A＝1のとき、3B＋4C＝7は、B＝C＝1となるので、うまくいきません。

い）A＝2のとき、3B＋4C＝14です。

　　C＝1なら、3B＝10となるので、うまくいきません。

う）A＝3のとき、3B＋4C＝21＝3×7です。

　　Cが3の倍数のときにうまくいく可能性があります。

　　C＝3のとき、3B＝9は、A＝B＝C＝3でうまくいきません。

　　C＝6のとき、3B＝−3でうまくいきません。

え）A＝4のとき、3B＋4C＝28＝3×8＋4です。

　　Cが3の倍数より1大きいときにうまくいく可能性があります。

　　C＝1のとき、3B＝24は、B＝8でうまくいきます。 → A＝4、B＝8、C＝1

　　C＝4のとき、3B＝12は、A＝B＝C＝4でうまくいきません。

　　C＝7のとき、3B＝0でうまくいきません。

お）A＝5のとき、3B＋4C＝35＝3×11＋2です。

　　Cが3の倍数より2大きいときにうまくいく可能性があります。

　　C＝2のとき、3B＝27は、B＝9でうまくいきます。 → A＝5、B＝9、C＝2

　　C＝5のとき、3B＝15は、A＝B＝C＝5でうまくいきません。

　　C＝8のとき、3B＝3は、B＝1でうまくいきます。→ A＝5、B＝1、C＝8

か）A＝6のとき、3B＋4C＝42＝3×14です。

　　Cが3の倍数のときにうまくいく可能性があります。

　　C＝3のとき、3B＝30でうまくいきません。

　　C＝6のとき、3B＝18は、A＝B＝C＝6でうまくいきません。

　　C＝9のとき、3B＝6は、B＝2でうまくいきます。→ A＝6、B＝2、C＝9

き）A＝7のとき、3B＋4C＝49＝3×16＋1です。

　　Cが3の倍数より1大きいときにうまくいく可能性があります。

　　C＝1のとき、3B＝45でうまくいきません。

　　C＝4のとき、3B＝33でうまくいきません。

　　C＝7のとき、3B＝21は、A＝B＝C＝7でうまくいきません。

く）A＝8のとき、3B＋4C＝56＝3×18＋2です。

　　Cが3の倍数より2大きいときにうまくいく可能性があります。

　　C＝2のとき、3B＝48でうまくいきません。

　　C＝5のとき、3B＝36でうまくいきません。

　　C＝8のとき、3B＝24は、A＝B＝C＝8でうまくいきません。

け）A＝9のとき、3B＋4C＝63＝3×21です。

　　Cが3の倍数のときにうまくいく可能性があります。

　　C＝3のとき、3B＝51でうまくいきません。

　　C＝6のとき、3B＝39でうまくいきません。

　　C＝9のとき、3B＝27は、A＝B＝C＝9でうまくいきません。

問2

問1の式（＊）7A＝3B＋4Cにおいて、

あ）A＝0とすると、3B＋4C＝0となり、うまくいきません。

い）B＝0とすると、7A＝4Cとなるので、A＝4、B＝0、C＝7

う）C＝0とすると、7A＝3Bとなるので、A＝3、B＝7、C＝0

その2

問1

その1の問1より、7A＝3B＋4Cです。

ここで、Aは、A、B、Cの中で、最大でも最小でもありません。

もし、最大とすると、b、cを正の数として、B＝A−b、C＝A−cと表せます。

すると、7A＝3(A−b)＋4(A−c)より、0＝−3b−4cとなります。

もし、最小とすると、ｂ、ｃを正の数として、B＝A＋b、C＝A＋cと表せます。

すると、7A＝3(A＋b)＋4(A＋c)より、0＝3b＋4cとなります。

この両方とも成り立ちません。

あ）B＞A＞Cとすると、b、cを正の数として、B＝A＋b、C＝A−cと表せます。

すると、7A＝3(A＋b)＋4(A−c)より、3b＝4cとなるので、b＝4、c＝3です。

（b＝8、c＝6は、ありえません。B、Cの少なくともどちらかが、9より大か1より小となります）

Aとしてあり得るのは、4か5です。

すると、(A，B，C)＝(4，8，1)、(A，B，C)＝(5，9，2)

い）B＜A＜Cとすると、b、cを正の数として、B＝A−b、C＝A＋cと表せます。

すると、7A＝3(A−b)＋4(A＋c)より、3b＝4cとなるので、b＝4、c＝3です。

（b＝8、c＝6は、ありえません。B、Cの少なくともどちらかが、9より大か1より小となります）

Aとしてあり得るのは、5か6です。

すると、(A，B，C)＝(5，1，8)、(A，B，C)＝(6，2，9)

問2

問1のあ）でAとして、3もありえるので、(A，B，C)＝(3，7，0)

問1のい）でAとして、4もありえるので、(A，B，C)＝(4，0，7)

NO3「浜田明巳」 　　03/22 10時01分　受信 更新 4/16

問１．条件より，
　　(１００Ａ＋１０Ｂ＋Ｃ)＋(１００Ａ＋１０Ｃ＋Ｂ)＋(１００Ｂ＋１０Ａ＋Ｃ)＋(１００Ｂ＋１０Ｃ＋Ａ)
　　　＋(１００Ｃ＋１０Ａ＋Ｂ)＋(１００Ｃ＋１０Ｂ＋Ａ)
　　　　　＝６(１００Ａ＋１０Ｂ＋Ｃ)
　　∴１６２Ｂ＋２１６Ｃ＝３７８Ａ
　　∴３Ｂ＋４Ｃ＝７Ａ・・・(1)
　(1)において，mod ３で計算すると，Ｃ≡Ａ（mod ３）
　Ａ≠Ｃ，Ａ，Ｃは１桁の整数から，
　　{Ａ，Ｃ}＝{１，４}，{１，７}，{２，５}，{２，８}，{３，６}，{３，９}，{４，７}，{５，８}，{６，９}・・・(2)
　(1)において，mod ４で計算すると，−Ｂ≡−Ａ（mod ４）
　　∴Ａ≡Ｂ（mod ４）
　Ａ≠Ｂ，Ａ，Ｂは１桁の整数から，
　　{Ａ，Ｂ}＝{１，５}，{１，９}，{２，６}，{３，７}，{４，８}，{５，９}・・・(3)
　(1)において，mod ７で計算すると，３Ｂ−３Ｃ≡０（mod ７）
　　∴３Ｂ≡３Ｃ（mod ７）
　３，７は互いに素なので，Ｂ≡Ｃ（mod ７）
　Ｂ≠Ｃ，Ｂ，Ｃは１桁の整数から，
　　{Ｂ，Ｃ}＝{１，８}，{２，９}・・・(4)
　(3)，(4)から，
　　(Ａ，Ｂ，Ｃ)＝(１，９，３)，(４，８，１)，(５，１，８)，(５，９，２)，(６，２，９)，(９，１，８)
　さらに(2)を考えると，
　　(Ａ，Ｂ，Ｃ)＝(４，８，１)，(５，１，８)，(５，９，２)，(６，２，９)
　答は，４８１，５１８，５９２，６２９の４個の数である．

問２．問１において，Ａ＝０，または，Ｂ＝０，またはＣ＝０とすればよい．
i). Ａ＝０のとき，(1)から，３Ｂ＋４Ｃ＝０・・・(5)
　Ａ，Ｂ，Ｃは相異なる１桁の整数なので，Ｂ＞０，Ｃ＞０
　これは(5)に矛盾する．
ii). Ｂ＝０のとき，(1)から，４Ｃ＝７Ａ
　４，７は互いに素であり，Ａ，Ｃは異なる１桁の整数なので，(Ａ，Ｃ)＝(４，７)
iii). Ｃ＝０のとき，(1)から，３Ｂ＝７Ａ
　３，７は互いに素であり，Ａ，Ｂは異なる１桁の整数なので，(Ａ，Ｂ)＝(３，７)
　i).〜iii).から，新たに入る２数は，３７０，４０７である．

（別解）間違えて数学的に解いてしまった．
　以下VBSCRIPTで解いてみる．

for j=1 to 0 step -1
   if j=1 then
    kotae=""
   else
    kotae=kotae&chr(13)&chr(13)
   end if
   kosuu=0
   for a=j to 9
    for b=j to 9
     if (a-b)*(a-b)>0 then
      for c=j to 9
       if (a-c)*(a-c)>0 and (b-c)*(b-c)>0 then
        if (a*100+b*10+c)+(a*100+c*10+b)+(b*100+a*10+c)+(b*100+c*10+a)+(c*100+a*10+b)+(c*100+b*10+a)=(a*100+b*10+c)*6 then
         kosuu=kosuu+1
         if kosuu>1 then
          kotae=kotae&chr(13)
         end if
         kotae=kotae&kosuu&":"&(a*100+b*10+c)
        end if
       end if
      next
     end if
    next
   next
next
msgbox kotae

（感想）親切にも解の個数について言及しなくても良かったのではないか，と思いました

NO4「にいばりZ12」　　　03/24 00時06分　受信 更新 4/16

3桁の数字ＡＢＣの桁を並び替えて得られる（ＡＢＣを含めて）６つの数の平均が、ちょうどもとの数ＡＢＣになるような数字について、次の問に答えよ。ただし、問２では百の位に０となったときは2桁の数字とする。

問１：Ａ，Ｂ，Ｃが1から９の相異なる数のとき、このような数字が４つある。すべて求めよ。

問２：Ａ，Ｂ，Ｃが０から９の相異なる数のとき、このような数字があと２つ増える。これらを求めよ。

準備

　　　並べ替えて得られる数は次の₃P₃＝6通り

　　　ABC

　　　ACB

　　　BAC

　　　BCA

　　　CAB

　　　CBA

　　　　これらの合計は2・(100・(A+B+C)+ 10・(A+B+C)+ (A+B+C) )＝222・(A+B+C)・・・・（A）

問１

6つの数の平均がＡＢＣとなるので

　　222・(A+B+C)/6＝100A+10B+C

変形整理すると

7A −3B−4C＝0　　　　　　　　　　　

さらに変形すると

　　3/4＝(C-A)/(A-B) 　 C>A>B               ・・・�@ （分子分母を正とする）

　　3/4＝(A-C)/(B-A) 　 C<A<B               ・・・�A （分子分母を正とする）

A,B,Cは9以下の異なる自然数なので

B＝A±4　 A＝C±3　 B＝C±7　（複合同順）・・・�B

∵　B＝A±8　 A＝C±6　 B＝C±14　（複合同順）とすると「（A,B,）Cは9以下の異なる自然数」に反します

�BからBの取りうる数は1,2,8,9

また�Bを満たすABCは

518,629,481,592・・・・・・・・・回答

問2

問1において�BからBの取りうる数は0,1,2,7,8,9

�Bを満たすABCは問1の回答

518,629,481,592に加え

407,370・・・・・・・・・回答

＊この時Bが0の時の　BAC,BCA及びCが0の時のCAB,CBAは2桁の数となりますが

Aは�@,�Aより0となることがないので、ABCは3桁の数になります。

「にいばりZ12」　　　03/28 00時24分　受信 更新 4/16

今回の問題は確認していませんが、前回のオイラーの無限乗積の応用に関する入試問題は2006年の九大，2008年の東京医科歯科大，2009年の新潟大，2010年の北大等で出題されているそうです。

<水の流れ：3桁でなくて、2桁から9桁に拡張して考えてみてください＞

返信にあった考察ですが（問１と同じ条件で考えます）

１）２桁の場合

ABを並べ替えるとBAとなり異なる２数の平均はそのどちらにもならないのでoutです。

２）4桁の場合

ABCDを並べ替えると₄P₄＝4!＝24通りで各々の桁に出現する数は24/4=6回づつでみな同じ回数です

従ってその総数は(6・10³+6・10²+6・10¹+6・10⁰)・ (A+B+C+D)で平均は

6666(A+B+C+D)/24＝1111(A+B+C+D)/4

となり (A+B+C+D)が4で割り切れなければoutです。

ここでこの問題を一般化してみます

前提

・各桁の数は相異なる1から９の数

・桁数をｎとする（1≦n≦9）

・求める数の各桁の数をK₁,K₂, K₃・・K_i・・,K_nとする(問1のA,B, C・・・に対応)

並べ替えの場合の数は

_nP_n＝n!

各桁におけるK_iの出現回数は同じなのでその回数は

_nP_n/n＝n!/n＝(n-1)!

よって並べ替えた数の合計は

(n-1)!・(10^n-1+10^n-2+・・・+10⁰)・(K₁+K₂+ K₃+・・K_i・・+K_n)

でその平均は

(n-1)!・(10^n-1+10^n-2+・・・+10⁰)・(K₁+K₂+ K₃+・・K_i・・+K_n)/n!

＝ (10^n-1+10^n-2+・・・+10⁰)・(K₁+K₂+ K₃+・・K_i・・+K_n)/n

上式の(10^n-1+10^n-2+・・・+10⁰)がｎと互いに素であれば

(K₁+K₂+ K₃+・・K_i・・+K_n)/nは割り切れたとしても１桁の自然数となります

これをAとし(10^n-1+10^n-2+・・・+10⁰)を乗じると

平均はAAAA・・・となる為、題意にそぐわず成立しません。

R(n)=(10^n-1+10^n-2+・・・+10⁰)を素因数分解してみます

R(3)=3*37

R(4)=11*101

R(5)=41*271

R(6)=3*7*11*13*37

R(7)=239*4649

R(8)=11*73*101*137

R(9)=3*3*37*333667

以上よりnとR(n)が互いに素ではないのはR(3)を含め

R(6)

R(9)

のみなのでこれらについて検討します

先ず簡単な方R(9)から考えます。Kの組み合わせは₉C₉=1で

(K₁+K₂+ K₃+・・K_i・・+K_n)は1+2+3+4+5+6+7+8+9＝45と確定しているので

組み合わせた数の総和の平均は

3*3*37*333667*45/9＝37*333667*45＝555555555となりout

次にR(6)を考えます。Kの組み合わせは₉C₆=504通りあります。

そこで問１で行ったように不定方程式を立ててみます

3・7・11・13・37・(K₁+K₂+K₃+K₄+K₅+K_６)/6＝10⁵K₁+10⁴K₁+10³K₁+10²K₁+10¹K₁+10⁰K₁

7・11・13・37・(K₁+K₂+K₃+K₄+K₅+K_６)/2＝10⁵K₁+10⁴K₂+10³K₃+10²K₄+10¹K₅+10⁰K₆

上式左辺は平均値であり自然数でなければなりません

従って(K₁+K₂+K₃+K₄+K₅+K_６)は偶数でなければならないのでkは偶数個の奇数を含まなければなりません

１から９までの奇数は1,3,5,7,9なので偶数個の奇数とは

２個か４個になります(0個は偶数のみとなり6に足りません)

奇数２個の場合

奇数の組み合わせは₅C₂＝10通りで残り4個の偶数は2,4,6,8の1通りで確定しますので結局次の10通り

1,3,2,4,6,8

1,5,2,4,6,8

1,7,2,4,6,8

1,9,2,4,6,8

3,5,2,4,6,8

3,7,2,4,6,8

3,9,2,4,6,8

5,7,2,4,6,8

5,9,2,4,6,8

7,9,2,4,6,8

7・11・13・37＝37037

ですが(K₁+K₂+K₃+K₄+K₅+K_６)/2を上記の最大である7,9,2,4,6,8

で計算すると18であり37・18＝666で37037・18の上3桁と下3桁が同じになってしまいます。よって上記全てout

奇数4個の場合

37・(K₁+K₂+K₃+K₄+K₅+K_６)/2を4桁以上にするため

(K₁+K₂+K₃+K₄+K₅+K_６)が最大となる組み合わせから考えます

3,5,7,9,6,8が(K₁+K₂+K₃+K₄+K₅+K_６)が最大となる組み合わせですがこれも

(K₁+K₂+K₃+K₄+K₅+K_６)/2は19で

37・19＝703

となり上3桁と下3桁が同じになってしまいます

従って6桁の数で成立する組み合わせも存在しない事になります。

結局題意を満たすのは3桁の場合のみとなってしまいました。

そこで3桁の場合を再度上記一般化した考え方で検証してみます

平均値は

3・37・(K₁+K₂+K₃)/3＝10²K₁+10¹K₂+10⁰K₃

37・(K₁+K₂+K₃)＝10²K₁+10¹K₂+10⁰K₃

Kの組み合わせは₉C₃=84通りあります。

ここでは6桁のような偶奇の縛りは出てきません

式変形し下記の不定方程式を解けばよいことになります。

7K₁-3K₂-4K₃＝0

以下前回の回答の通りです。

3桁の場合しか成立しないという結果に驚いてしまいました。

「にいばりZ12」　　　04/08 01時12分　受信 更新 4/16

問2と同じ条件で考えてみます

１）２桁の場合

ABを並べ替えるとBAとなり異なる２数の平均はそのどちらにもならないのでoutです。

これは問1の条件と同じです

ここでこの問題を一般化してみます

前提

・各桁の数は相異なる0から９の数

・桁数をｎとする（1≦n≦10）

・求める数の各桁の数をK₁,K₂, K₃・・K_i・・,K_nとする(問2のA,B, C・・・に対応)

並べ替えの場合の数は

_nP_n＝n!

各桁におけるK_iの出現回数は同じなのでその回数は

_nP_n/n＝n!/n＝(n-1)!

よって並べ替えた数の合計は

(n-1)!・(10^n-1+10^n-2+・・・+10⁰)・(K₁+K₂+ K₃+・・K_i・・+K_n)

でその平均は

(n-1)!・(10^n-1+10^n-2+・・・+10⁰)・(K₁+K₂+ K₃+・・K_i・・+K_n)/n!

＝ (10^n-1+10^n-2+・・・+10⁰)・(K₁+K₂+ K₃+・・K_i・・+K_n)/n

上式の(10^n-1+10^n-2+・・・+10⁰)がｎと互いに素であれば

(K₁+K₂+ K₃+・・K_i・・+K_n)/nは割り切れたとしても１桁の自然数となります

これをAとし(10^n-1+10^n-2+・・・+10⁰)を乗じると

平均はAAAA・・・となる為、題意にそぐわず成立しません。

R(n)=(10^n-1+10^n-2+・・・+10⁰)を素因数分解してみます

R(1)=1

R(2)=11

R(3)=3*37

R(4)= R(2)*V(2)＝11*101

R(5)=41*271

R(6)= R(3)*V(3)=3*37*7*11*13=3*7*11*13*37

R(7)=239*4649

R(8)= R(4)*V(4)＝11*101*73*137＝11*73*101*137

R(9)= R(3)*1001001＝3*37*3*333667＝3*3*37*333667

R(10)= R(5)*V(5) ＝41*271*11*9091＝11*41*271*9091

美しい数学の話第１3話　「100…001の因数分解」より引用

V(i)=10 ⁱ+1

V(1)=11

V(2)=101

V(3)=7*11*13

V(4)=73*137

V(5)=11*9091

以上よりnとR(n)が互いに素ではないのはR(3)を含め

R(6)

R(9)

のみなのでこれらについて検討します

R(6)を考えます。Kの組み合わせは₁₀C₆=210通りあります。(前回此処で計算間違いをしていました₉C₆=84通りでした)

そこで問2で行ったように不定方程式を立ててみます

3・7・11・13・37・(K₁+K₂+K₃+K₄+K₅+K_６)/6＝10⁵K₁+10⁴K₁+10³K₁+10²K₁+10¹K₁+10⁰K₁

7・11・13・37・(K₁+K₂+K₃+K₄+K₅+K_６)/2＝10⁵K₁+10⁴K₂+10³K₃+10²K₄+10¹K₅+10⁰K₆

上式左辺は平均値であり自然数でなければなりません

従って(K₁+K₂+K₃+K₄+K₅+K_６)は偶数でなければならないのでkは偶数個の奇数を含まなければなりません

0から９までの奇数は1,3,5,7,9なので偶数個の奇数とは

２個か４個になります(0個は偶数のみとなり6に足りません)

奇数２個の場合

奇数の組み合わせは₅C₂＝10通りで残り4個の偶数は₅C₂＝10通りで結局次の100通り

7・11・13・37＝37037

ですが(K₁+K₂+K₃+K₄+K₅+K_６)/2を上記の最大である7,9,2,4,6,8（ここは問1と同じ）

で計算すると18であり37・18＝666で37037・18の上3桁と下3桁が同じになってしまいます。よって上記全てout

奇数4個の場合

37・(K₁+K₂+K₃+K₄+K₅+K_６)/2を4桁以上にするため

(K₁+K₂+K₃+K₄+K₅+K_６)が最大となる組み合わせから考えます

3,5,7,9,6,8が(K₁+K₂+K₃+K₄+K₅+K_６)が最大となる組み合わせですがこれも

(K₁+K₂+K₃+K₄+K₅+K_６)/2は19で

37・19＝703

となり上3桁と下3桁が同じになってしまいます

従って6桁の数で成立する組み合わせは存在しない事になります。

R(9)を考えます。Kの組み合わせは₁₀C₉=10で

(K₁+K₂+ K₃+・・K_i・・+K_n)は1+2+3+4+5+6+7+8+9＝45と、

K_iを0に置き換えた次の数です

45-1＝44（0,2,3,4,5,6,7,8,9）

45-2＝43（0,1,3,4,5,6,7,8,9）

45-3＝42（0,1,2,4,5,6,7,8,9）

45-4＝41（0,1,2,3,5,6,7,8,9）

45-5＝40（0,1,2,3,4,6,7,8,9）

45-6＝39（0,1,2,3,4,5,7,8,9）

45-7＝38（0,1,2,3,4,5,6,8,9）

45-8＝37（0,1,2,3,4,5,6,7,9）

45-9＝36（0,1,2,3,4,5,6,7,8）

上記を組み合わせた数の総和の平均は

R(9)*45/9＝37*333667*45＝555555555となりout

以下同様に計算すると

543209876

530864197

518518518 　　out

506172839

493827160

481481481 　　out

469135802

456790123

444444444　　 out

強引に計算しましたが先生の仰る通り6通りで成立する事が解りました

ここでもう少し考えます

そもそも

R(9)* (K₁+K₂+ K₃+・・K_i・・+K_n)/9

において

R(9)＝111111111です

(K₁+K₂+ K₃+・・・・+K₉)/9

は自然数となる（割り切れる）場合1桁になります（∵K_max≦9）

従って、(K₁+K₂+ K₃+・・・・+K₉)が45と36の場合outになるのが解ります

また、R(9)/3＝37037037なので

R(6)の時の議論と同様に

(K₁+K₂+ K₃+・・・・+K₉)が9の因数を持つ場合outになるのが解ります。

しかしながら、それ以外の時にすべて成立している理由がよく解からないのでもう少ししつこく考えてみます。

投稿には間に合わないかもしれません・・・・。

NO5「三角定規」　　　　 04/10 22時52分　受信 更新 4/16

● 第345回応募問題解答＜三角定規＞

　3桁（もしくは2桁）の数を N 1＝100a＋10b＋c（a，b，cは0以上の異なる整数）とする。

　N 1＝の各桁の数を並べ替えてできる数は

　　N 2＝100a＋10c＋b

　　N 3＝100b＋10c＋a

　　N 4＝100b＋10a＋c

　　N 5＝100c＋10a＋b

　　N 6＝100c＋10b＋a

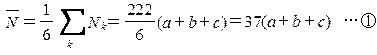
題意より 37(a＋b＋c)＝100a＋10b＋c …�A

　整理して −7a＋3b＋4c＝0 …�B

　�Bより 3b＋4c≡3b−3c≡3(b−c)≡0 (mod 7) …�C

　�Cより

　　(1) b，cが0以外のとき (b，c)＝(1，8)，(8，1)，(2，9)，(9，2)

　　　 �Bより，(a，b，c)＝(5，1，8)，(6，2，9)，(4，8，1)，(5，9，2) …[答]

(2) b，cが0になれるとき，(1)の他 (a，b，c)＝(4，0，7)，(3，7，0) が増える。…[答]

NO6「二度漬け白菜」 04/11 10時50分　受信 更新 4/16

[解答]

(問1) 求める4つの数は，481,518,592,629. (答)

(問2) 新たに2つ増える数は，370,407. (答)

(問1)
3桁の数字ABCの桁を並べ替えて得られる6つの整数の合計は，
222*(A+B+C)である．
題意が満たされるとすれば，
222*(A+B+C)/6 = 100*A+10*B+C
つまり，
3*(B-C)=7*(A-C) --- (★)
を満たすような正整数A,B,C (ただしA,B,Cは全て異なり，
なおかつ全て9以下) の組(A,B,C)が存在する．
(★)より，B-C=-7 または B-C=7 の2つの可能性がある．

(1) B-C=-7 の場合
(★)より，A-C=-3となる．よって A=C-3．
C=B+7≧8であるから，C=8 or C=9．
C=8のとき，B=1,A=5.
C=9のとき，B=2,A=6.
よって2つの組:(A,B,C)=(5,1,8),(6,2,9)が得られる．

(2) B-C=7 の場合
(★)より，A-C=3となる．よって A=C+3．
B=C+7≧8であるから，B=8 or B=9．
B=8のとき，C=1,A=4.
B=9のとき，C=2,A=5.

よって2つの組:(A,B,C)=(4,8,1),(5,9,2)が得られる．

以上より，題意を満たす3桁の数は，518,629,481,592
の4通りの可能性があることがわかる．
これらの4通りの解は，確かに題意を満たす3桁の数
であることが確認できる．

(問2)

(★)を満たすような非負整数A,B,C (ただしA,B,Cは全て異なり，
なおかつ全て9以下)の組(A,B,C)を考える．
(問1)のときと同様に，B-C=-7 または B-C=7 の2つの可能性がある．

B-C=-7 の場合には，
C=B+7≧7であるから，C=7の可能性が新たに加わる．
このとき，B=0,A=4となる．

また，B-C=7 の場合には，
B=C+7≧7であるから，B=7の可能性が新たに加わる．
このとき，C=0,A=3となる．

以上より，題意を満たす3桁の数として，407 と 370
が新たに加わる可能性があることがわかる．
この2つの数 407,370 はいずれも題意を満たす3桁の数
であることが確認できる．

今回の問題の出典は，ピーター・フランクルさんの著書だそうですね．
次の問題は，今から20年近く前に ピーター・フランクルさんが
或る数学雑誌に出題していたものです．
気が向いたら考えてみてください．

-------------------------------------------------

(問題)
2^n - 1 の全ての素因数が 2^(n/1998) 以下であるような
自然数 n が存在するだろうか？

-------------------------------------------------

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。