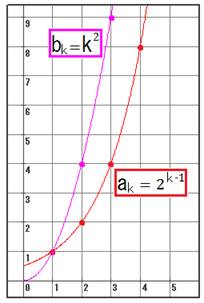
�����Q�X�N�P�O���Q�X��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��352�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF10���P���`10��29����
�m�a�̗L�E���n
�@���i�����P���灇�j�P�^���Q�@�����Q�^�U���P�D�U�S�S�X�R�E�E�E�ƂȂ邱�Ƃ͒m���Ă��܂��B���L�̂悤�ȁg�a�̗L�E���h���ؖ�������͍��Z���ł�������͈͂ł��B

���o�T�F�u��w�̐��w�v2012�N2������
NO1�u���N���̂�������v 10/03 18��04���@��M �X�V 10/29
���1
����1�A���� ![]() �̖������䋉���́A2�Ɏ������܂��B
�̖������䋉���́A2�Ɏ������܂��B
����Ɣ�r���čl���܂��B
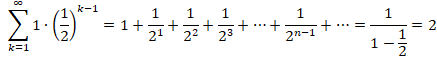
��n���܂ł̘a�́A2�����������Ȃ�܂��B
![]()
![]()
 2�̐���
2�̐��� ![]() ��
�� ![]() �́A�����͓������ł����A
�́A�����͓������ł����A
����ȊO�̍��́A ![]() �̕����傫�Ȓl���Ƃ�܂��B
�̕����傫�Ȓl���Ƃ�܂��B
���̐��̑召�Ƃ��̋t���̑召�Ƃ́A���ɂȂ�܂��B
![]() �Ȃ�A
�Ȃ�A ![]() �ł��B
�ł��B
����āA
![]()
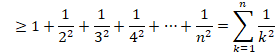
���2
![]() �Ȃ̂ŁA
�Ȃ̂ŁA ![]() �ł��B
�ł��B
�������̋t���̘a�ɂ��āA��2���ȍ~��A������2���̐ς̋t���ɒu�������āA
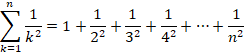
![]()
![]()
![]()
![]()
���3
![]() �Ȃ̂ŁA
�Ȃ̂ŁA ![]() �ł��B
�ł��B
�������̋t���̘a�ɂ��āA�q���g�̎��ɒu�������āA
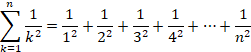
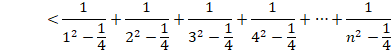
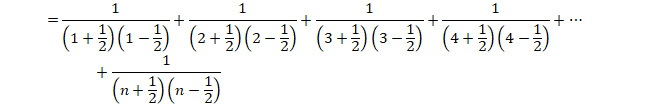
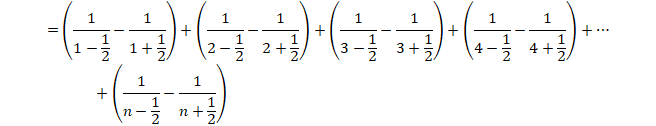
![]()
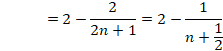
![]()
���4
(1)
���̐��̑召�Ƃ��̋t���̑召�Ƃ́A���Ȃ̂ŁA
![]()
![]()
����āA
![]()
![]()
![]()
����ƁA���̌��́A ![]() �ł��B
�ł��B
(2)
���̖����l����Ƃ��́A
![]()
�ƂȂ邎�̌��Ƃ����������₷���ł��B
���̌��́A ![]() �ł��B
�ł��B
1�jm��1�̂Ƃ��A ![]() �ƂȂ邎�́A����1��1��
�ƂȂ邎�́A����1��1��
2�j����2�̂Ƃ��A ![]() �ƂȂ邎�́A����2, 3��2��
�ƂȂ邎�́A����2, 3��2��
3�j����3�̂Ƃ��A ![]() �ƂȂ邎�́A����4, 5, 6, 7��4��
�ƂȂ邎�́A����4, 5, 6, 7��4��
�E�E�E
n�j����k�̂Ƃ��A ![]() �ƂȂ邎�́A
�ƂȂ邎�́A ![]() ��
�� ![]() ��
��
����Ă���1���炎��2k�|1�܂ł̕������̋t���̘a�i ![]() ����
���� ![]() �܂ł̘a�j�́A
�܂ł̘a�j�́A
���̎��ŗ}���邱�Ƃ��ł��܂��B
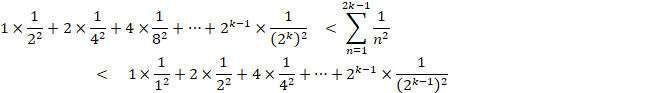
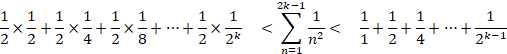
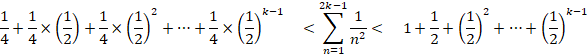
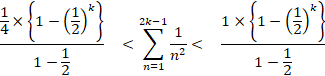
����āA
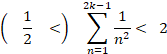
�i�@�j�́A k �� �� �̂Ƃ��ł��B
���5
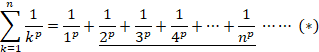
�ɂ��Ē��ׂ܂��B
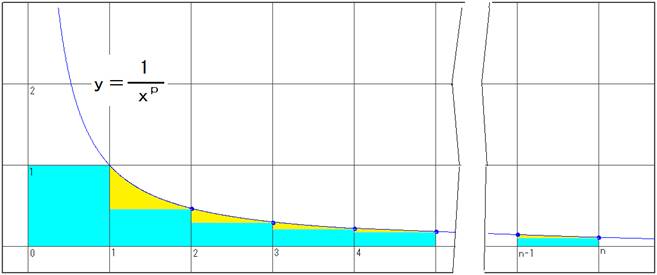
���̃O���t�́A ![]() �ł��B
�ł��B
(*)�͉��̃O���t�����F�̕����̖ʐςł��B
���̃O���t�̂���1���炘�����܂ł̒�ϕ��́A���F�����F�̕��������킹���ʐςł��B
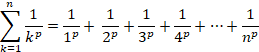
![]()
![]()
![]()
����1�Ȃ̂ŁA��p�|1�́A������ɔ��U����̂ŁA���̋t����0�Ɏ������܂��B
NO2�u�l�c�����v �@�@10/04 11��03���@��M �X�V 10/29
���P
�@�}���C�P�������Q�̂Ƃ��C�P�^�Q�Q���P�^���Q
�@�@�@�@�@�@�Q�������R�̂Ƃ��C�P�^�R�Q���P�^���Q
�@�@�@�@�@�@�R�������S�̂Ƃ��C�P�^�S�Q���P�^���Q
�@�@�@�@�@�@�E�E�E
�@�@�����P���������P�^���Q���P�{���P�������������^���Q
�@�@�@�@�@�@�@�@�@�@�@�@�@���P�|[�P�^��]�P��������
�@�@�@�@�@�@�@�@�@�@�@�@�@���P�|(�P�^���|�P)
�@�@�@�@�@�@�@�@�@�@�@�@�@���Q�|�P�^��
�@�@�@�@�@�@�@�@�@�@�@�@�@���Q
�@�@�����P���������P�^���Q���Q�@
���Q
�@�����Q�̂Ƃ��C���Q�����Q�|������(���|�P)���O
�@�@���P�^���Q���P�^{��(���|�P)}
�@�@�@�@�@�@�@�@���P�^(���|�P)�|�P�^��
�@�@�����P���������P�^���Q���P�{���Q���������P�^���Q
�@�@�@�@�@�@�@�@�@�@�@�@�@���P�{���Q��������{�P�^(���|�P)�|�P�^��}
�@�@�@�@�@�@�@�@�@�@�@�@�@���P�{(�P�|�P�^��)
�@�@�@�@�@�@�@�@�@�@�@�@�@���Q
�@�@�����P���������P�^���Q���Q
���R
�@�����P�̂Ƃ��C
�@�@���Q�����Q�|�P�^�S���O
�@�@���P�^���Q���P�^(���Q�|�P�^�S)
�@�@�@�@�@�@�@�@���P�^{(���|�P�^�Q)(���{�P�^�Q)}
�@�@�@�@�@�@�@�@���P�^(���|�P�^�Q)�|�P�^(���{�P�^�Q)
����C
�@�@���P���������P�^���Q�����P��������{�P�^(���|�P�^�Q)�|�P�^(���{�P�^�Q)}
�@�@�@�@�@�@�@�@�@�@�@�@���Q�|�P�^(���{�P�^�Q)
�@�@�@�@�@�@�@�@�@�@�@�@���Q
�@�@�����P���������P�^���Q���Q
���S
�@�i�P�j�������P�^���Q�C�P�^�Q�Q�����������P�^�Q�Q�i���|�P�j����C
�@�@�P�^�Q�Q�����P�^���Q���P�^�Q�Q�i���|�P�j
�@�@���Q�Q(���|�P)�����Q���Q�Q��
�@�����O����C�Q���|�P�������Q��
�@���C���͐����Ȃ̂ŁC�Q���|�P�{�P�������Q���|�P
�@�̂ɂ��̌��́C
�@�@(�Q���|�P)�|(�Q���|�P�{�P)�{�P���Q���|�P�|�P�i�j
�@�i�Q�j�����������̂Ƃ��C
�@�@���Q���|�P�������Q���|�P�P�^���Q
�@�@�@��(�P�^�Q���|�P)�Q�{{�P�^(�Q���|�P�{�P)}�Q�{{�P�^(�Q���|�P�{�Q)}�Q�{�E�E�E�{{�P�^(�Q���|�P)}�Q
�@�@�@��(�P�^�Q���|�P)�Q�E�Q���|�P
�@�@�@��(�P�^�Q)���|�P
�ł��邩��C�Q���|�P�������Q���|�P�̂Ƃ��C
�@�@���P���������P�^���Q�����P�������Q���|�P�P�^���Q
�@�@�@�@�@�@�@�@�@�@�@�@���P�{�P�^�Q�{(�P�^�Q)�Q�{�E�E�E�{(�P�^�Q)���|�P
�@�@�@�@�@�@�@�@�@�@�@�@��{�P�|(�P�^�Q)��}�^(�P�|�P�^�Q)
�@�@�@�@�@�@�@�@�@�@�@�@���Q{�P�|(�P�^�Q)��}
�@�@�@�@�@�@�@�@�@�@�@�@���Q�|(�P�^�Q)���|�P
�@�@�@�@�@�@�@�@�@�@�@�@���Q
�@�@�����P���������P�^���Q���Q
���T
�@�����P�ł���C���P�Ɠ��l�ɁC
�@�@���P�����������|����lim���������P�����������|��
�@�@�@�@�@�@�@�@�@�@�@��lim������(�P�{���P�����������|������)
�@�@�@�@�@�@�@�@�@�@�@���P�{lim������{�P�^(�P�|��)�E[���P�|��]�P��������}
�@�@�@�@�@�@�@�@�@�@�@���P�{lim�������P�^(�P�|��)�E(���P�|���|�P)
�@�@�@�@�@�@�@�@�@�@�@���P�|�P�^(�P�|��)
�@�@�@�@�@�@�@�@�@�@�@���P�{�P�^(���|�P)
�@�̂Ƀ��P�����������|���͗L���ł���C����o���P�����������|���p�͒P����������ł���D
�@�̂Ƀ��P�����������|���͎�������D
NO3�u��x�Ђ����v 18/18
21��56���@��M �X�V 10/29
���1�F
�C�ӂ̒萔 p (p��1) �ɑ��āC���̕s���������藧�D
��[k=1..n](1/k^p) �� p/(p-1) -
1/((p-1)*n^(p-1))
(�ؖ�)
n=1�̂Ƃ��́C
(����)=��[k=1..1](1/k^p)=1�C
(�E��)=p/(p-1)-1/(p-1)=1
�ł��邩��C�m���ɕs���������藧�D
n��2�̂Ƃ����l����D
������ k ����сCk��x��k+1 �����悤�� x �ɑ��āC
0��1/(k+1)^p �� 1/x^p �����藧�D����āC
��[x=k,k+1](1/(k+1)^p)dx �� ��[x=k,k+1](1/x^p)dx
�܂�C
1/(k+1)^p �� ��[x=k,k+1](1/x^p)dx
���̎��ŁCk=1,2,�c,n-1 �Ƃ����C�ӁX������ƁC
��[k=1..n-1](1/(k+1)^p) �� ��[k=1..n-1]��[x=k,k+1](1/x^p)dx
�܂�C
��[k=2..n](1/k^p) �� ��[x=1,n](1/x^p)dx
= 1/(p-1)-1/((p-1)*n^(p-1))
����āC
��[k=1..n](1/k^p) ��
p/(p-1)-1/((p-1)*n^(p-1))
(�ؖ��I)
���̕s�����ƁCp/(p-1)-1/((p-1)*n^(p-1))��p/(p-1) �ł��邱�ƂƂ���C
��[k=1..n](1/k^p) �� p/(p-1) ---(��)�@
�ł��邱�Ƃ��킩��D
p=2�̂Ƃ����l���āC
��[k=1..n](1/k^2) �� 2
�ƂȂ�D
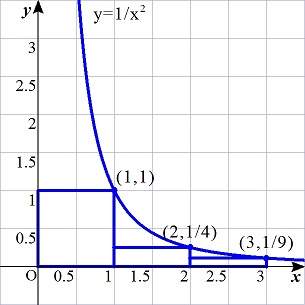
���2�F
n=1�̂Ƃ��́C��[k=1..n](1/k^2)=1��2�ł���D
n��2�̂Ƃ����l����D
k��2�̂Ƃ��Ck^2��k*(k-1)��0 �ł��邩��C1/k^2��1/(k*(k-1))�D
����āC
��[k=1..n](1/k^2)
=1+��[k=2..n](1/k^2)
��1+��[k=2..n](1/(k*(k-1)))
=1+��[k=2..n](1/(k-1)-(1/k))
=1+(1-1/2)+(1/2-1/3)+ �c +(1/(n-1)-1/n)
=2-1/n
��2�D
�ȏ���C�C�ӂ̐����� n �ɑ��āC
��[k=1..n](1/k^2) �� 2
�����藧���Ƃ��������D
���3�F
k��1�̂Ƃ��Ck^2��k^2-1/4��0 �ł��邩��C1/k^2��1/(k^2-1/4)�D
����āC
��[k=1..n](1/k^2)
����[k=1..n]1/(k^2-1/4)
=��[k=1..n]4/(4*k^2-1)
=2*��[k=1..n](1/(2*k-1)-1/(2*k+1))
=2*((1/1-1/3)+(1/3-1/5)+ �c +(1/(2*n-1)-1/(2*n+1))
=2*(1-1/(2*n+1))
=2-2/(2*n+1)
��2�D
���4�F
(1)
1/2^(2*m)��a[n]��1/2^(2*(m-1)) ���
1/2^(2*m)��1/n^2��1/2^(2*(m-1))�D
������C2^(m-1)��n��2^m�D
��������悤�� n �̌��́C
2^m - 2^(m-1) - 1 = 2^(m-1) -1 �� (��)
(2)
1/2^(2*m)��a[n]��1/2^(2*(m-1))
�����悤�� n �̌��͍��X 2^(m-1) �D
����āC1/2^(2*m)��a[n]��1/2^(2*(m-1))��
�������悤�ȍ� a[n] �����̘a�́C
(2^(m-1))*(1/2^(2*(m-1)))=1/(2^(m-1)) �ȉ��ł���D
����āC
��[k=1..n](1/k^2)
=��[k=1..n]a[k]
����[k=1..2^n]a[k]
����[m=1..n+1]1/(2^(m-1))
=2-(1/2)^n
��2�D
���5�F
���� {S[n]} (n=1,2,3,�c) ���C
S[n]=��[k=1..n](1/k^p)
�Œ�`����D
�S�Ă̐����� n �ɑ��āCS[n+1]��S[n]��0 �����藧�D
�܂��C���1 �Ŏ������s���� (��) ����C
�S�Ă̐����� n �ɑ��āC|S[n]|��p/(p-1)
�ł��邱�Ƃ��킩��D
�ȏ�̂��Ƃ��� ���� {S[n]} �͎�������D
�܂�C��������
��[k=1..��](1/k^p)
�͎�������D
-------------------------------------------------
��[k=1..��](1/k)^2 = ��^2/6
�ł��邱�Ƃ́C���̂悤�ɍl������Z���w�͈̔͂�
�ؖ��ł���悤�ł��D
�ȉ��̏ؖ��́C
�w���M�I �����ʋ����w�o�g�� �ߋE��w���w�R���e�X�g���W�x (���{�]�_��)
�Ƃ����{�́C167�`169�łɂ�����̂��Q�l�ɂ��܂����D
��[k=1..��](1/k)^2 = ��^2/6
(�ؖ�)
�h�E���A�u���̌���:
cos(m*��)+i*sin(m*��)=(cos(��)+i*sin(��))^m
�ɂ����āC�E�ӂ�藝���g���ēW�J����ƁC
(�E��)
=(cos(��)+i*sin(��))^m
=(sin(��))^m*(cot(��)+i)^m
=(sin(��))^m*��[k=0..m]comb(m,k)*(i^k)*(cot(��))^(m-k)�D
����āC
cos(m*��)+i*sin(m*��)=(sin(��))^m*��[k=0..m]comb(m,k)*(i^k)*(cot(��))^(m-k)
�ƂȂ�D���ӂ̋������Ƃ�ƁC
sin(m*��)=(sin(��))^m*��[k=0..floor((m-1)/2)]comb(m,2*k+1)*((-1)^k)*(cot(��))^(m-2*k-1)�D
�����ŁCm=2*n+1 �Ƃ����ƁC
sin((2*n+1)*��)=(sin(��))^(2*n+1)*��[k=0..n]comb(2*n+1,2*k+1)*((-1)^k)*((cot(��))^2)^(n-k)
�ƂȂ�D
f(x)=��[k=0..n]comb(2*n+1,2*k+1)*((-1)^k)*x^(n-k) �Ƃ����ƁC
f(x)�� x �� n ���������ł����āC��̓�����
sin((2*n+1)*��)=(sin(��))^(2*n+1)*f((cot(��))^2)
�Ə�����D
0��x����/2 �̂Ƃ��Csin(��)��0�D���̂Ƃ��C
f((cot(��))^2)=0
�� sin((2*n+1)*��)=0
�� (2*n+1)*��=k*�� (k=1,2,�c,n)
���������āCf(x)=0�ƂȂ�悤�� x �́C
x=(cot(k*��/(2*n+1)))^2 (k=1,2,�c,n)
�ł���C����炪���ׂĂł���D
��[k]=(cot(k*��/(2*n+1)))^2
(k=1,2,�c,n) �Ƃ����ƁC
f(x)=(2*n+1)*(x-��[1])*(x-��[2])*�c*(x-��[n])
�ƈ��������ł���D���ƌW���̊W���C
��[k=1..n](cot(k*��/(2*n+1)))^2
=��[k=1..n]��[k]
=(1/(2*n+1))*comb(2*n+1,3)
=n*(2*n-1)/3 --- (����)
0��x����/2 �̂Ƃ��C�s����
0��sin(x)��x��tan(x)
�����藧�D���̕ӁX��2�悵�C�t�����Ƃ�ƁC
(cot(x))^2��(1/x)^2��1+(cot(x))^2
��D
���̕s������ x=k*��/(2*n+1) �������C����� R=(��/(2*n+1))^2 ���|����ƁC
R*(cot(k*��/(2*n+1)))^2��(1/k)^2��R*(1+(cot(k*��/(2*n+1)))^2)�D
k=1 ���� n �܂Řa���Ƃ�ƁC
R*��[k=1..n](cot(k*��/(2*n+1)))^2����[k=1..n](1/k)^2��R*��[k=1..n](1+(cot(k*��/(2*n+1)))^2)�D
������(����)��p���āC
n*(2*n-1)*��^2/(3*(2*n+1)^2)����[k=1..n](1/k)^2��2*n*(n+1)*��^2/(3*(2*n+1)^2)
��D�����ŁC
lim[n����]n*(2*n-1)*��^2/(3*(2*n+1)^2)
= ��^2/6�C
lim[n����]2*n*(n+1)*��^2/(3*(2*n+1)^2)
= ��^2/6
�ł��邩��C�͂��݂����̌������C
lim[n����]��[k=0..n](1/k)^2 = ��^2/6
��D(�ؖ��I)
�����̗���F���̏ؖ��͍��Z���̂������ł������Ȃ̂ŁA����̐l�ɒm���Ă��炢�����B��
�u�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
