�����R�O�N�S���P�T��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��358�����w�I�ȉ����
�@�@�@�@����W���ԁF�R��18���`�S��15����
�m���ʂȎ��R���n
�u�W���j�A���w�I�s���s�b�N�ւ̒���v�i���{�]�_�ЁF�����N�璘�j�Ƃ����{����o�肵�܂��B
���P�@����4���̎��R���ŁA���S�������ł���A���̂ǂ̌��̐�����8�ȉ��ł���B���̊e���ɂP�������Ăł��鐔�����S�������ɂȂ�Ƃ����B���̂悤�Ȃ��������߂�B
���Q�@�S���̎��R�����ŁA13�̔{���ł���A13���̉�3����378�ɂȂ�悤�Ȃ��̂����ׂċ��߂�B
���R�@���R�����̐擪�ɐ����Q�����������A�����ɐ����P�����������ē����鐔�́A33���ɓ������Ƃ����B���̂悤�Ȃ����P������B
NO1�u�l�c�����v �@�@03/19 15��10���@��M �X�V 4/15 �@
���P�C�Q
�@�u�a�r�b�q�h�o�s�ʼn������D
���R�i�W�V�͂��������邪�C��ʓI�ɉ����Ă݂�j
�@�ȉ�mod �P�O�Ōv�Z����D
�@�R�R���߂P�ł���C
�@�@�R�R�E�P�߂R
�@�@�R�R�E�R�߂X
�@�@�R�R�E�T�߂T
�@�@�R�R�E�V�߂P
�@�@�R�R�E�X�߂V
���C
�@�@���߂V
�@���V�~�R�R���Q���V�P�ł��邩��C�������ŕ\���ƁC�����P�O���{�V�ł���C
�@�@(�P�O���{�V)�~�R�R���Q�O�O�O�E�E�E�O�V�P�{�P�O�O��
�@�@���Q�R�O�����Q�O�O�O�E�E�E�O�V�P�|�Q�R�P
�@�@���Q�R�O(���{�P)���Q�O�O�O�E�E�E�O�V�O
�@�@���Q�R(���{�P)���Q�O�O�O�E�E�E�O�V
�@�̂ɁC
�@�@�Q�~�P�O���{�V�߂O�imod �Q�R�j
�ƂȂ�Q�ȏ�̐����������߂�悢�D�ȉ�mod �Q�R�Ōv�Z����D
�@�Q�~�W�{�V�߂O�ł��邩��C�P�O���߂W�ƂȂ邍�����߂�悢�D
�@�@�P�O�Q���P�O�O�߂W
�@�@�P�O�R�߂W�O�߂P�P
�@�@�P�O�S�߂P�P�O�߁|�T
�@�@�P�O�T�߁|�T�O�߁|�S
�@�@�P�O�U�߁|�S�O�߂U
�@�@�P�O�V�߂U�O�߁|�X
�@�@�P�O�W�߁|�X�O�߂Q
�@�@�P�O�X�߂Q�O�߁|�R
�@�@�P�O�P�O�߁|�R�O�߁|�V
�@�@�P�O�P�P�߁|�V�O�߁|�P
�@�@�P�O�P�Q�߁|�P�O
�@�@�P�O�P�R�߁|�P�O�O�߁|�W
�@�̂Ɏ��ɂW�ɓ������Ȃ�̂́C
�@�@�P�O�Q�S�߂P�O�P�P�E�P�O�P�R��(�|�P)�E(�|�W)���W
�@�̂ɂ����Q�C�Q�{�Q�Q�C�Q�{�Q�Q�E�Q�C�E�E�E�ƂȂ�̂ŁC
�@�@�����Q�{�Q�Q(���|�P)���Q�Q���|�Q�O�i���͐������j
�@�@������(�Q�~�P�O�Q�Q���|�Q�O�{�V)�^�Q�R�|�P
�@�@�������P�O���{�V���P�O�E(�Q�~�P�O�Q�Q���|�Q�O�{�V)�^�Q�R�|�R
�@�����P�̂Ƃ��C
�@�@�����P�O�E(�Q�~�P�O�Q�{�V)�^�Q�R�|�R���W�V�i�R�R�����Q�W�V�P�j
�@�����Q�̂Ƃ��C
�@�@�����P�O�E(�Q�~�P�O�Q�S�{�V)�^�Q�R�|�R
�@�@�@�E�E�E
�u�l�c�����v �@�@03/22 15��04���@��M �X�V 4/15
���R�i�����j
�@�@����(�Q�~�P�O�Q�Q���|�P�X�{�P)�^�Q�R
�@�����Q�̂Ƃ��C
�@�����R�̂Ƃ��C
NO2�u���N���̂�������v 03/19 17��12���@��M �X�V 4/15
���1
n�̕�������A�Ƃ��܂��B
n�̊e����1�������Ăł��鐔�̕�������A�{a�Ƃ��܂��B
�܂�A���̎������藧���܂��B
(A�{a)�~(A�{a)��A�~A�{1111�@����@(��)
![]() �@�@
�@�@![]()
32�~32��1024�@�@1024�{1111��2135�@�@![]()
94�~94��8836�@�@8836�|1111��7725�@�@![]()
�܂��AA��A�{a�́A32����94�͈̔͂ɂ���܂��B
31��菬�����ƁA4���̐��ɂȂ�܂���B
95���傫���Ɛ�̈ʂ�9�̐����A100�����5���̐��ɂȂ��Ă��܂��܂��B
A�́A87��菬�����Ȃ�܂��B
������傫���ƁA������1111���������Ƃ�8836���傫���Ȃ邩��ł��B
A�{a�́A46���傫���Ȃ�܂��B
�����菬�����ƁA������1111���������Ƃ��A1024��菬�����Ȃ�����ł��B
(��)�������܂��B
�W�J���Đ�������ƁA
a(2A�{a)��1111��11�~101
����āAa��11�AA��45
n��A�~A��45�~45��2025
���2
n��13a �Ƃ����܂��B
13n��13�~13a��169a �ł��B
a�̈�̈ʂ��l���܂��B
169�~1��169�@�@169�~2��338�@�@169�~3��507�@�@169�~4��676�@�@169�~5��845
169�~6��1014�@ 169�~7��1183�@ 169�~8��1352 �@169�~9��1521�@ 169�~0��000
��1����8�ɂȂ�̂́A2�ł��B
a�̏\�̈ʂ��l���܂��B
169�~2��338�̏\�̈ʂ�3�ɉ����āA7�ƂȂ�̂�4�ŁA�\�̈ʂ́A6�ł��B
a�̕S�̈ʂ��l���܂��B
��̓I�Ɏ����܂��B
169�~162��27378�@169�~262��44278�@169�~362��61178�@169�~462��78078�@169�~562��94978
169�~662��111878�@169�~762��128778�@169�~862��145678�@169�~962��162578�@169�~062��10478
n��13�~162��2106
���3
n��ab���k �Ƃ��܂��B
2ab���k1��33�~ab���k �ł��B
n�̉�1���̐������l���܂��B
3�~k �̉�1����1�ƂȂ�̂ŁA���̌v�Z�����āAk��7�ł��B
3�~1��3�@�@3�~2��6�@�@3�~3��9�@�@3�~4��12�@�@3�~5��15
3�~6��18�@3�~7��21�@3�~8��24�@3�~9��27�@3�~0��0
n�̍ŏ�ʂ̐���a���l���܂��B
��̌v�Z���݂�a�́A7�A8�A9�̂ǂꂩ�ł��B
���ׂĂ����܂��B
�En��1���̂Ƃ��A
�@271
�@33�~7��231���A�K���܂���B
�En��2���̂Ƃ��A
�@2771
�@33�~77��2541���A�K���܂���B
�@2871
�@33�~87��2871���A�K���܂��B
�@2971
�@33�~97��3201���A�K���܂���B
n��1�́A87�ł��B
NO3�u�ɂ���Z12�v�@�@�@03/27 22��16���@��M
�X�V 4/15
���1
����4���̎��R���ŁA���S�������ł���A���̂ǂ̌��̐�����8�ȉ��ł���B���̊e���ɂP�������Ăł��鐔�����S�������ɂȂ�Ƃ����B���̂悤�Ȃ��������߂�B
m2+1111��������������邽�߂ɂ�
m2+2am+a2+1111-2am-a2
�ɂ�����
1111-2am-a2��0�E�E�E�@
�ƂȂ�悢
m =(1111-a2)/(2a)�E�E�E�A
���ꂪ�����Ȃ̂ŕ��q�������łȂ�����͎��R���ƂȂ�Ȃ�
�@�����a�͊
�@m�͕��ł��\��Ȃ������ׂ�Ώ\���Ȃ̂�a�����Ƃ���
�܂��Am2��8888�ȉ�1000�ȏ�Ȃ̂�
32��m��94
�@
����m��32�y��94������a�����߂��
a2+2am-1111��0
a=-m+��(m2+1111)
m=32�̎�
a=-32+��2135��7
m=94�̎�
a=-94+��9947��13
�����a��7�ȏ�13�ȉ��̊�ɂ��ćA�������邩�ǂ����ׂ�Ƃ�������܂�
a=7�̎�
�@m =(1111-49)/14��1062/14��531/7�E�E�E�����Ȃ�
a=9�̎�
�@m =(1111-81)/18��1030/18��515/9�E�E�E�����Ȃ�
a=11�̎�
�@m =(1111-121)/22��990/22��45�E�E�E������
a=13�̎�
�@m =(1111-169)/26��942/26��471/13�E�E�E�����Ȃ�
�����a=9�̎��ɂ���m2+1111�͎��R���ŕ����������Ȃ����Ƃ�����܂���
���̎���m2�̊e����8�ȉ��ł��邱�Ƃ������Ă����Ȃ���Ȃ�܂���
m2��452��2025
��8�ȉ��ł�
����������
n��2025�E�E�E�E�E�E��
�in��1111������������3136��562)�E�E�E�֑�
���Q�@
�S���̎��R�����ŁA13�̔{���ł���A13���̉�3����378�ɂȂ�悤�Ȃ��̂����ׂċ��߂�B
��ӂ�݂͂��˂��̂Ŗ��@�ƇA�ɏ������������Ă��������܂��B
�@
4���̎��R��n������
m=13n�Ƃ���
m�̉�3����378�ƂȂ�悤��n�����ׂċ��߂�
�悸�A13�̔{���ʼn��ꌅ��8�ɂȂ�P�[�X���l���܂�
�����13�~6��78�����Ȃ��̂�n�̉��ꌅ��6�ɂȂ�܂�
�܂��A���߂�4���̎��R��n�̍ő��9996�ŏ���1006�B
n=1000a+100b+10c+6 (0<a��9,0��b��9, 0��c��9��a,b,c�͔���)
m=13n=13000a+1300b+130c+13�E6
m�̉�3���ɂ�a�͖��W���������āAa��1����9�܂ł̂��ׂĂ��Ƃ�
1300b��1000b+300b
���̎��E��1���ڂ�m�̉�3���ɖ��W
�����m�̉�3�����l����Ƃ�
300b+130c+78
�̉�3����378�ƂȂ���̂��l����悢
b=0�̎�130c�̉�3����300
�@����́A0��c��9�ł͑��݂��Ȃ��̂�out
b=1�̎�130c�̉�3����000�Ȃ̂�c=0
b=2�̎�130c�̉�3����700
�@����́A0��c��9�ł͑��݂��Ȃ��̂�out
���l��b=3����9�ł��ׂ�out�i30c�̉�2���ڂ�1��c��9�͈̔͂�0�ɂȂ�Ȃ��j
����ċ��߂�n��
1106,2106,�E�E�E�E,9106�E�E�E��
�A
4���̎��R��n������An��13�̔{���ł���
m=13n�Ƃ���
m�̉�3����378�ƂȂ�悤��n�����ׂċ��߂�
�@
�E�@�̉̒���13�̔{���ƂȂ���̂��l���܂�
������̂�2016�݂̂ł��B
�@�@2106�E�E�E��
���R�@���R�����̐擪�ɐ����Q�����������A�����ɐ����P�����������ē����鐔�́A33���ɓ������Ƃ����B���̂悤�Ȃ����P������B
���R�����̐擪�ɐ����Q�����������A�����ɐ����P�����������ē����鐔��m�Ƃ��܂�
�@m�̖�����1�Ȃ̂�n�̖�����7��������܂���B
n��1���̏ꍇ���l���܂�
n=7��33����231��out
n��2���̏ꍇ���l���܂�(m��4���ɂȂ�܂�)
n=10a+7
m =33��=330a+231
m�̈ꌅ�ڂ�2�ƂȂ�悤��a��6,7,8��������܂���B
���̂Ƃ��A
m��2211�A2541�A2871
����ɓڂƎO���ڂ�n�ƂȂ�̂�2871�����ł�
����āAn=87�E�E�E�E��
���z�G���炭�Ԃ�̓��e�Ő��w�ł͂Ȃ��͂����̌v�Z�ɂȂ��Ă��܂����悤�ȋC�����܂��B
�����v��������܂��lj����e�������Ǝv���܂�
�u�ɂ���Z12�v�@�@�@04/07 22��45���@��M �X�V 4/15
n��k���̏ꍇ���l���܂�
�@�@m=2�~10k+1+1+10n
�@�@�@�ƂȂ�܂���
�@�@�@m=33n�łȂ���Ȃ�Ȃ��̂�
m=2�~10k+1+1+10n=33n
n=(2�~10k+1+1)/23
k=2�̎�n=87����ӂ���܂�܂��E�E�E�E�ʉ�
�������
2�~10k+1+1��0�@�imod23�j
�@�@�@�̎���k�����߂��n�̌���������܂�
2�~10k+1��-1��22�@�imod23�j
����k=2�̂Ƃ�
�@�@�@2�~10k+1��22�@�imod23�j
�@����������̂������Ă���̂�
�@�@�@k=3�̂Ƃ�
�@�@�@�@22�~10=220��13�@�imod23�j
�@�@�@�@������܂�
�@�@�@�@���l��k=4�̂Ƃ�
�@�@�@�@13�~10=130��15�@�imod23�j
�@�@�@�Ƌ��߂Ă�����
�@�@�@�@2�~10k+1��23�Ŋ��������̂��܂��
�@�@�@�@�@12,5,4,17,9,21,3,7,1,10,8,11,18,19,6,14,2,20,16,22
�@�@�@�@�@�ƂȂ�k=24,46,68�E�E�E�̂Ƃ�22�ƂȂ�܂��B
�@�@�@�@�@���̌v�Z�̂��܂�͏z����̂�s��0�ȏ�̐����Ƃ�
�@�@�@�@k=2+22s
�@�@�@�@�@�̂Ƃ�
�@�@2�~10k+1��22�@�imod23�j���������邱��
�@�@�@����m��33n�ɓ������Ȃ�悤��n�����R���͈̔͂Œ�܂邱�Ƃ�����܂��B
�@�@�@���݂�s=1�̎�k=24��m�̌�����26�ƂȂ�܂���
�@�@�@n=(2�~1025+1)/23��869,565,217,391,304,347,826,087
�ƂȂ�܂��B
���̂��Ƃ���u���̂悤�Ȃ����P��������v�̑�ӂ�����܂��B
�P���ł����M�Z�ł��Ƃ₽�璷���v�Z�ɂȂ肻���̓��ӂȐl���L���ƂȂ��Ă��܂��܂��B�i���́A(�G�N�Z���ł�16���܂ł����v�Z�ł��Ȃ��̂�)���������mod�����g���Čv�Z���܂����j
�u�ɂ���Z12�v�@�@�@04/11 23��01���@��M �X�V 4/15
���1�������l�������Ă݂܂���
����4���̎��R���ŁA���S�������ł���A���̂ǂ̌��̐�����8�ȉ��ł���B���̊e���ɂP�������Ăł��鐔�����S�������ɂȂ�Ƃ����B���̂悤�Ȃ��������߂�B
m�𐮐��Ƃ�n��m2�Ƃ��܂�
m2+1111��������������邽�߂ɂ�
m2+2am+a2+1111-2am-a2
�ɂ�����
1111-2am-a2��0�E�E�E�@
�ƂȂ�悢
m =(1111-a2)/(2a)�E�E�E�A
���ꂪ�����Ȃ̂ŕ��q�������łȂ�����͎��R���ƂȂ�Ȃ�
�@�����a�͊
�A�͎��̂悤�ɕό`�ł��܂�
m =(1111/a-1)/2-(a-1)/2
�E�ӑ�2���͐����Ȃ̂ő�1���ɂ�����a��1111�̖łȂ���Ȃ�Ȃ�
1111��f�������������
11�~101
�����
a =11,101
m =�}45
n= m2 =2025�E�E�E�E�E�ʉ�
NO4�u��x�Ђ����v 04/06 11��09���@��M
�X�V 4/15
[���1]
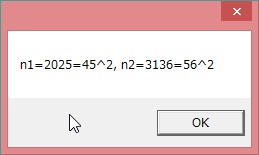
���������悤�� n ��, n=2025 �̂݁D(��)
n=a^2�Cn+1111=b^2 (a�Cb �͐�����)�@�Ƃ�����D
����2�����C
b^2-a^2=1111�C �܂�
(b-a)*(b+a)=11*101�@�ƂȂ�D����āC
(b-a)=11 ���@(b+a)=101
�܂��́C
(b-a)=1 ���@(b+a)=11*101�C �܂�
(a,b)=(45,56) �܂��� (a,b)=(555,556)
�ƂȂ邪�Cn=a^2 �� 4���̐������ɂȂ�̂� (a,b)=(45,56)�̂Ƃ��̂݁D
a=45�̂Ƃ��Cn=a^2=45^2=2025�ƂȂ��āCn�̂��ׂĂ̌��̐�����8�ȉ��D
����Ė�蕶�̏��������悤�� n �́Cn=2025 �̂݁D.
[���2]
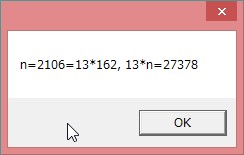
���������悤�� n ��, n=2106 �̂݁D(��)
n=1000*a+100*b+10*c+d
(a�Cb�Cc�Cd �͐����ł����āC1��a��9�C0��b,c,d��9 )�@
�Ƃ�����D
8��13*n��13*d (mod 10) �ł��邩��Cd=6�D
78��13*n��13*(10*c+d)��13*(10*c+6)��130*c+78 (mod 100) �ł��邩��C
0��130*c (mod 100)�D
����āCc=0�D
378��13*n��13*(100*b+10*c+d)��13*(100*b+6)��1300*b+78 (mod 1000) �ł��邩��C
300��1300*b (mod 1000)�D�@
����āCb=1�D
�ȏ��� n=1000*a+106 �ƂȂ邪�Cn �� 13 �̔{���ƂȂ�̂́Ca=2
�̂Ƃ��̂݁D
[���3]
��蕶�̏��������悤�� n �̈��́C
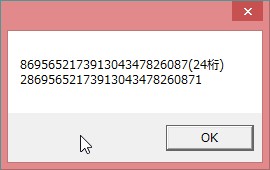
n=8695652173913043478260869565217391304347826087 (��)
n �̌����� m (m��1) �Ƃ����,
10^(m-1)��n��10^m�D
n �̐擪�ɐ��� 2 �����������C�����ɐ��� 1 �����������ē����鐔�́C
2*10^(m+1)+10*n+1 �ł���D���ꂪ 33*n �ɓ���������C
2*10^(m+1)+10*n+1=33*n �܂�C2*10^(m+1)+1=23*n�D
����āC
2*10^(m+1)��-1��22(mod 23)
�܂�C
10^(m+1)��11(mod 23)
�����藧�K�v������D
�����ŁC
10��10�C10^2��8�C10^3��11�C10^4��18�C10^5��19�C10^6��6�C10^7��14�C10^8��2�C
10^9��20�C10^10��16�C10^11��22�C10^12��13�C10^13��15�C10^14��12�C10^15��5�C
10^16��4�C10^17��17�C10^18��9�C10^19��21�C10^20��3�C10^21��7�C10^22��1�C
10^23��10�C10^24��8�C10^25��11(mod 23) �c
�ł���̂ŁC
m+1=22*k+3 (k��0�ȏ�̔C�ӂ̐���)
�Ƃ�����K�v������D
���̂Ƃ��Cn=(2*10^(22*k+3)+1)/23 �ƂȂ�D
����ɂ��̂Ƃ��Cn �� m=22*k+2 ���̐����ƂȂ�D
���ہC(n,m)=((2*10^(22*k+3)+1)/23, 22*k+2)�ł���Ƃ��C
10^m - n
=10^(22*k+2)-(2*10^(22*k+3)+1)/23
=(3*10^(22*k+2)-1)/23
��0�C
n-10^(m-1)
=(2*10^(22*k+3)+1)/23-10^(22*k+1)
=(177*10^(22*k+1)+1)/23
��0
�ł���̂ŁC
10^(m-1)��n��10^m�D
�ȏ���C��蕶�̏��������悤�Ȑ����� n �́C
n=(2*10^(22*k+3)+1)/23 (k��0�ȏ�̔C�ӂ̐���)
�őS�Ăł���D
n=(2*10^(22*k+3)+1)/23 �ɂ����� k=2 �Ƃ���ƁC
n=8695652173913043478260869565217391304347826087
��D
�ȏ�D
�@�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
