�����R�O�N�W���T��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��362�����w�I�ȉ����
�@�@�@�@����W���ԁF�V���W���`�W���T����
�m���[�U�[�̉~�n
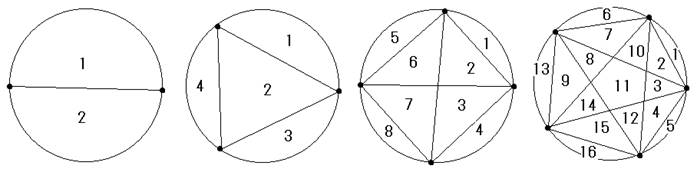
�@�����[��������܂��B����́A����F�P�C�Q�C�S�C�W�C�P�U,�E�E�E�v
��6���͈�̂ǂ�Ȑ�������ł��傤���B
�ߋ��A�����V���ؗj���łɂ��������ł��B���ꂪ���̖��ł�
�~�����n�̓_�����A���������ׂĒ����Ō��ԁB���̂Ƃ��o����̈�̍ő�� �����ŕ\�킹�B�܂��A���̐���̓p�X�J���̎O�p�`�̒��ɉB��Ă��܂��B�������Ă݂Ă��������B
���F���̖���1969�N�Ƀ��I�E���[�U�[�iLeo
Moser�j�����߂Ė����N�����̂ŁA
���[�U�[����ƌĂ�Ă���B
NO1�u��x�Ђ����v 07/14 14��06���@��M
�X�V 8/5
[��]
���߂�ő���� n �ŕ\�킷�ƁC
(1/24)*(n^4-6*n^3+23*n^2-18*n+24)
�ƂȂ�D
����͓W���̕����a
C(n-1,0)+C(n-1,1)+C(n-1,2)+C(n-1,3)+C(n-1,4)
�ɓ������D(��)
n��3�Ƃ��čl����D
�~����� n �̓_�_�Ƃ����n�p�`�� G �Ƃ���D
G �� n*(n-3)�{�̑Ίp���̂����C�ǂ�3�{�� ��_�Ō����
���Ƃ��Ȃ����l����D���̏������ɂ����ĉ~������
����Ăł���̈�̌��� f(n) �Ƃ���D
f(n)�����߂�ő���ł���D
G�̕ӂƉ~�̌ʂō����̈�͑S���� n ����D
G�̕ӂ�G�̑Ίp���Ƃō����̈�̌��� a(n) �Ƃ���D
f(n)=n+a(n) �ł���D
���܂��� a(n) �����߂�D
G�̕ӂ����G�̑Ίp���ɂ���āCG�͑����̓ʑ��p�`�ɍו�
�����D�ו����ꂽ�ʑ��p�`�S�̂̏W���� S �Ƃ���D
S�̌��̂����C�Ӑ����ő��̂��̂��Cm�p�`�ł���Ƃ���D
�܂�CG�̕ӂ����G�̑Ίp���ɂ���āCG�́C
3�p�`�C4�p�`�C5�p�`�C�c�Cm�p�`
�ɍו��������̂Ƃ���D
S�̌��̂����Cj�p�` (3��j��m)�̌��� r_j
�Ƃ���D
a(n)=r_3+r_4+r_5+�c+r_m�@�ł���D
j�p�`��j�̒��_�����D
�����S�̌��̒��_���̑��a�́C
3*r_3 + 4*r_4 + 5*r_5 + �c + m*r_m
�ƂȂ�D
S�̌��̒��_�́CG�̒��_��������G�̑Ίp���̌�_��
�ǂ��炩�ł���D
G�̔C�ӂ̒��_�� P �Ƃ���D
S�̌��̂����C P�_�ɂ����̂́C(n-2)�� ��������D
G�̔C�ӂ̑Ίp���̌�_�� Q �Ƃ���D
S�̌��̂����C Q�_�ɂ����̂́C4�� ��������D
G�̒��_���� n �CG�̑Ίp���̌�_���� C(n,4) �� �ł��邩��C���̓��������藧�D
3*r_3
+ 4*r_4 + 5*r_5 + �c + m*r_m = (n-2)*n + 4*C(n,4) ---
(1)
��j�p�`�̓��p�̘a�́C(j-2)*180�� �ł���D
����āCS�̌��̓��p�̘a�����v�������̂́C
r_3*(3-2)*180��+ r_4*(4-2)*180��+ r_5*(5-2)*180��+ �c + r_m*(m-2)*180��
=(r_3+2*r_4+3*r_5+
�c +(m-2)*r_m)*180��
�ł���D
G�̔C�ӂ̑Ίp���̌�_ Q �̎���̊p�x�̍��v�� 360��
�ł���CG�̓��p�̘a�� (n-2)*180���ł���̂ŁC���̓��������藧�D
(r_3+2*r_4+3*r_5+
�c +(m-2)*r_m)*180��= C(n,4)*360��+ (n-2)*180���D
����āC
r_3+2*r_4+3*r_5+ �c +(m-2)*r_m = 2*C(n,4)+(n-2) ---(2)
(1)-(2)���C
2*(r_3+r_4+r_5+�c+r_m)=2*C(n,4)+(n-1)*(n-2)�D
����āCr_3+r_4+r_5+�c+r_m=C(n,4)+(1/2)*(n-1)*(n-2)�D
�܂�Ca(n)=C(n,4)+(1/2)*(n-1)*(n-2)�D
����āC
f(n)
=n+a(n)
=n+C(n,4)+(1/2)*(n-1)*(n-2)
=(1/24)*(n^4-6*n^3+23*n^2-18*n+24)�D
(����� n=1�C2 �̂Ƃ��ɂ����������ʂ�^���鎮�ƂȂ��Ă���)
f(n)
=n+C(n,4)+(1/2)*(n-1)*(n-2)
=C(n,0)+C(n,2)+C(n,4)
=C(n-1,0)+C(n-1,1)+C(n-1,2)+C(n-1,3)+C(n-1,4)
�ł��邩��Cf(n)�̓p�X�J���̎O�p�`�̑� n �i�ڂɂ����āC
������5�Ԗڂ܂ł̒l�����v�������̂ɂȂ��Ă���D
(�ȏ�)
NO2�u���N���̂�������v 07/17 22��26���@��M �X�V 8/5
362�@���N���̂�������
���~����ɓ_���Ȃ���A�̈��1�ł��B
�~����ɓ_��1�Ȃ�A���ԑ��肪�Ȃ��̂ŗ̈��1�ƍl���܂��B
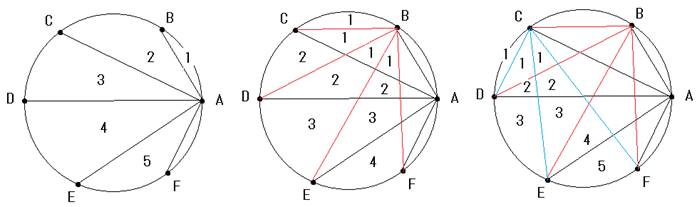
�_���A2����5�̂Ƃ��́A���̐}�̂悤�ɂȂ�܂��B
�_�̌��𐔗�̏��Ԃƍl����ƁA���̂悤�ł��B
![]()
���_��6�̏ꍇ���l���܂��B
���ɓ_������ł����A������̈�̌��𐔂��܂��B
(1)�_��6����������̏��߂̏�Ԃł́A�̈��{1}�ł��B
(2)�_A�ƁA���̓_(B�AC�AD�AE�AF)�����т܂��B
�@A��B��1�AA��C��1�AA��D��1�AA��E��1�AA��F��1�A���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�A1�A1�A1�A1}
(3)�_B�ƁA���̓_(C�AD�AE�AF)�����т܂��B
�@B��C��1�AB��D��2�AB��E��3�AB��F��4�A���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�A2�A3�A4}
(4)�_C�ƁA���̓_(D�AE�AF)�����т܂��B
�@C��D��1�AC��E��3�AC��F��5�A���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�A3�A5}
(5)�_D�ƁA���̓_(E�AF)�����т܂��B
�@D��E��1�AD��F��4�A���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�A4}
(6)�_E�ƁA�_F�����т܂��B
�@������̈�̌��́A{1}

����đ�6���́A
![]()
���_��n�̏ꍇ���l���܂��B
���ɓ_������ł����A������̈�̌��𐔂��܂��B
(1)�_��n����������̏��߂̏�Ԃł́A�̈��{1}�ł��B
(2)�_A1�ƁA���̓_(A2�AA3�AA4�A����AAn)�����т܂��B
�@����1�{�����������ƁA1���̈悪�����܂��B
�@������̈�̌��́A{1�A1�A1�A����A1}�@[����n�|1]
(3)�_A2�ƁA���̓_(A3�AA4�AA5�A����AAn)�����т܂��B
�@A2��A3��1�AA2��A4��2�AA2��A5��3�A����AA2��An��n�|2�A���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�A2�A3�A����An�|2}�@[����n�|2]
(4)�_A3�ƁA���̓_(A4�AA5�AA6�A����AAn)�����т܂��B
�@A3��A4��1�AA3��A5��3�AA3��A6��5�A����AA3��An��2n�|7���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�A3�A5�A����A2n�|7}�@[����n�|3]
���
(k)Ak-1�ƁA���̓_�iAk�AAk+1�AAk+2�A����AAn�j�����т܂��B
�@Ak-1��Ak��1�AAk-1��Ak+1��1+(k�|2)�AAk-1��Ak+2��1+2(k�|2)�A����AAk-1��An��1+(n�|k)(k�|2)���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�Ak�|1�A2k�|3�A����A(n�|k)k�|2(n�|k)+1}�@[����n�|k+1]
���
(n�|1) An-2�ƁA���̓_�iAn-1 �AAn�j�����т܂��B
�@An-2��An-1��1�AAn-2��An��1+(n�|3)�A���ꂼ��̈悪�����܂��B
�@������̈�̌��́A{1�An�|2}�@[����2]
(n) An-1�ƁA���̓_�iAn�j�����т܂��B
An-1��An��1�A�̈悪�����܂��B
�@������̈�̌��́A{1}�@[����1]
�ȏ�̗̈�̌�����ׂĂ݂܂��B
(1)�@�@1�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
[1��]
(2)�@�@1�A1�A1�A����������������A1�@�@�@�@�@�@�@�@�@[n�|1��]
(3)�@�@1�A2�A3�A���������An�|2�@�@�@�@�@�@�@�@�@�@�@[n�|2��]
(4)�@�@1�A3�A5�A����A2n�|7�@�@�@�@�@�@�@�@�@�@�@�@�@[n�|3��]
���
(k)�@�@1�Ak�|1�A2k�|3�A����A(n�|k)k�|2(n�|k)+1�@ �@[n�|k+1]
���
(n�|1) 1�An�|2�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@[2��]
(n)�@�@1�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@[1��]
�܂Ƃ߂�ƁA(1)�ԖڈȊO�A(k)�Ԗڂ́A����1�A����k�|2�̓�������ł��B
(k)�Ԗڂ̗̈�̌��̍��v�́A
![]()
![]()
(1) �Ԗڂ���(n)�Ԗڂ܂ł̗̈�̌��̍��v�����߂܂��B
(A) �̎���k��1�Ƃ���ƁA
![]()
![]()
�Ȃ̂ŁA
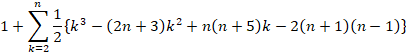
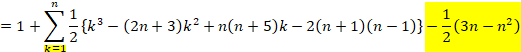
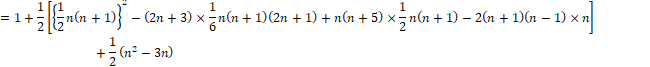
![]()
![]()
![]()
![]()
���p�X�J���̎O�p�`��W���ŕ\���ƁA���̂悤�ł��B
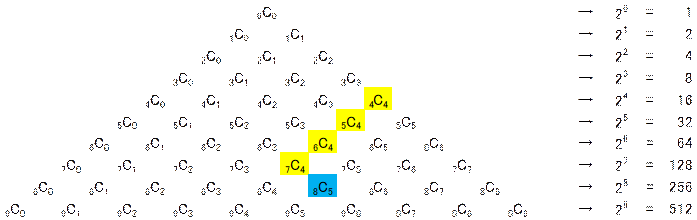
�p�X�J���̎O�p�`�́A�����т̓�̘a�̒l���������̒l�Ƃ����d�g�݂ɂȂ��Ă��܂��B
�܂�A![]() �ł��B
�ł��B
���̎����J��Ԃ��ėp����ƁA
![]()
![]()
![]()
![]()
�Ⴆ�A���F�̍��v�́A�Ƃ������Ƃł��B
�p�X�J���̎O�p�`����̓I�Ȑ��ŏ��������ƁA���̂悤�ł��B

�_�̌���9�̏ꍇ��(1)�Ԗڂ���(9)�Ԗڂ܂ł̐�����������ɕ��ׂ܂��B
��������̕��т̍��v���Ō�̍s�̉E���ɏ������ׂ܂��B
���F�̍��v���Ƃ������Ƃł��B
�Ō�̍s�̉����v�����߂鐔��̒l�ł��B

���̂悤�Ȏd�g�݂ŋ��߂��鉡���т̒l�����ɏ������ׂ�ƁA
���̉����т̐��̍��v���A(B)�̎��̋�̓I�Ȓl�ł��B
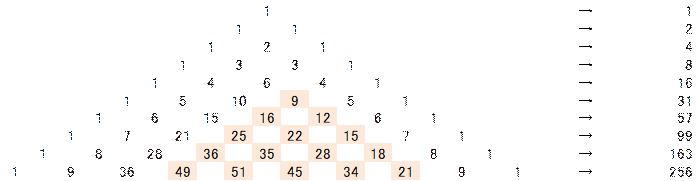
��̂悤�ɂȂ�܂��B
�i�������(A)�̕\�Ƃ������Ƃɂ��܂��j
�E�[�̒l�����ׂĂ��鐔��̒l�ł��B
���F�̕������A�p�X�J���̎O�p�`�ƒl���قȂ镔���ł��B
���p�X�J���̎O�p�`�̏ォ��n�Ԗڍ�����k�Ԗڂ̒l�́A![]() �ł��B
�ł��B
����Ǝ�(A)�Ƃ̍������߂�ƁA
![]()
![]()
![]()
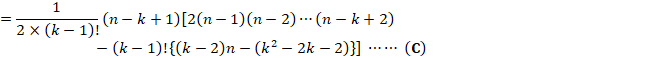
�Ⴆ�A��(C)�ŁAk=4�Ƃ���ƁA
![]()

![]()
�ł��B
���̎��ŁAn��6�Ƃ���ƁA
![]()
����́A�p�X�J���̎O�p�`�� ![]() ����A1�������ƁA(A)�̕\�̍ŏ��̐Ԃ�������9��\���܂��B
����A1�������ƁA(A)�̕\�̍ŏ��̐Ԃ�������9��\���܂��B
�u���N���̂�������v 07/18 14��28���@��M �X�V 8/5
<���N���̂�������@���w�E���肪�Ƃ��������܂����B
��(B)��4�����ł��闝�R���킩��܂����B
���Ƃ��猩��ƊȒP�Ȃ��Ƃ��Ǝv���܂����B��
����(A)�̕\�������܂��B

�p�X�J���̎O�p�`�������܂��B

������5�Ԗڂ܂ł̍��v���A��̕\�̉����v�ƈ�v���܂��B
������m�F���܂��B
![]()
![]()
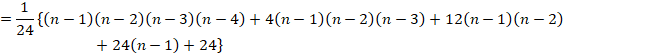
![]()
�ƂȂ�A��(B)�ƈ�v���܂��B
