�����R�O�N�X���R�O��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��364�����w�I�ȉ����
�@�@�@�@����W���ԁF�X���Q���`�X���R�O����
�m���_�̒ʉߖʐρn
�@
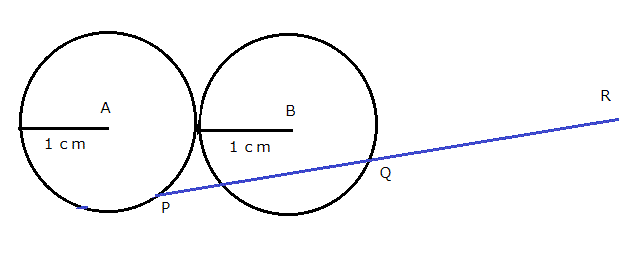
�}�̂悤�Ɍ݂��ɐڂ��锼�a�P�����̂Q�̉~�`�Ƃa������B
�~�`��ɓ_�o�A�~�a��ɓ_�p������A�_�p�Ɋւ���_�o�̑Ώ̓_��_�q�Ƃ���B
�_�o�Ɠ_�p�����ꂼ�ꎩ�R�ɉ~������Ƃ��A�_�q�̒ʉ߂���̈�̖ʐς����߂�B
�u���̏o�T�F�������̃R�}�吔�w�Ȃ���v
NO1�u�ɂ���Z12�v�@�@�@09/05 23��44���@��M �X�V 9/30
�\�z�����܂���
�~P��Q�̐ړ_�����_�Ƃ��A�e�~�̒��S��ʂ钼���������Ƃ����_�ɐ����Ȏ��������Ƃ��܂�
R�̎�肤����W�͉~(x-3)2+y2=32�̓����Ŋ���(x-3)2+y2=1�̊O���̃h�[�i�b�c�̕�����
�ʐς�8�ɂȂ�܂��B
�����܂ł��\�z�Ȃ̂ł�������ꂩ��ꐶ�����ؖ����Ă��������Ǝv���܂��B
�u�ɂ���Z12�v�@�@�@09/22 23��36���@��M
�X�V 9/30
���_��\�z������������Ă��Ă����܂��B
�\�z
�~P��Q�̐ړ_�����_�Ƃ��A�~P,Q�̒��S��ʂ钼���������Ƃ����_�ɐ����Ȏ��������Ƃ��܂�
R�̎�肤����W�͉~(x-3)2+y2=9�̓����Ŋ���(x-3)2+y2=1�̊O���̃h�[�i�b�c�̕�����
�ʐς�8�ɂȂ�܂��B
����
�@�~P
�@�@�@(x+1)2+y2=1�E�E�E�@
�~Q
�@�@�@(x-1)2+y2=1�E�E�E�A
1�j���A�~P��̓_P�Ɖ~Q��̓_Q�����Ԓ��������_(O)��ʂ�ꍇ���l���܂��B
�A��P=Q�ȊO�̎���P��Q��0�Ƃ��܂��B
���̎�R�̍��W�͎��̂悤�ɂȂ�܂��B
R��x���W�iX�j
�@�@�@�A��x���W��3�{
R��y���W�iY�j
�@�@�@�A��y���W��3�{
�ȏォ��
�@�@�@X=3x,Y=3y
�A���ɑ�������
�@�@�@�@(X -3)2+ Y 2=32�E�E�E�B
![]() �@�@�i���a3���S�i3,0�j�̉~
�@�@�i���a3���S�i3,0�j�̉~
�@���̎��A����POQR���܂ޒ����̕�������
![]() �@�@Y=aX�@�ia= tan -1�Ɓ@�G-��/2<��<��/2�j
�@�@Y=aX�@�ia= tan -1�Ɓ@�G-��/2<��<��/2�j
�܂��AP=Q=R�̎�Q��O�ւ̋߂Â����ɂ��
�@�@�@�@a =lim�Ɓ��}��/2
tan-1��=�}��
�@�@�@�@��2��̒l�i������y���Ɠ����j���Ƃ�܂��B
 ��L�����œ��l��
��L�����œ��l��
 P��0�i���_�j
P��0�i���_�j
Q��0�̏ꍇ���l���܂��B
![]()
![]()

 R��x���W�iX�j
R��x���W�iX�j
![]() �@�@�@�A��x���W��1�{
�@�@�@�A��x���W��1�{
R��y���W�iY�j
![]()
![]() �@�@�@�A��y���W��1�{
�@�@�@�A��y���W��1�{
![]()



![]()
 �ȏォ��
�ȏォ��
�@�@�@X=x,Y=y

![]()
![]() �A���ɑ�������
�A���ɑ�������
�@�@�@�@(X -3)2+ Y 2=12�E�E�E�B�f
![]() �i���a1���S�i3,0�j�̉~
�i���a1���S�i3,0�j�̉~
���l��
![]() P��0�i���_�j
P��0�i���_�j
Q��0�̏ꍇ���l���܂��B
![]() R��x���W�iX�j
R��x���W�iX�j
�@�@�@�A��x���W��2�{
R��y���W�iY�j
�@�@�@�A��y���W��2�{
�ȏォ��
�@�@�@X=2x,Y=2y
�A���ɑ�������
�@�@�@�@(X -2)2+ Y 2=22�E�E�E�C
�i���a2���S�i2,0�j�̉~
��
�~P��̓_P�Ɖ~Q��̓_Q�����Ԓ������l���܂��B
�@���̎��A�_P���Œ�i���W���ix0,y0�j���_Q�����_���玞�v���ɉ~Q���1�T�����܂��B
�_R��x���W�́iX�j
�@�A��x���W�~2- x0
�_R��y���W�́iY�j
�@�A��y���W�~2- y0
�ȏォ��
�@�@�@X=2x- x0,Y=2y- y0
�@�@�@(x,y)=((X+ x0)/2, (Y+ y0)/2)
�A���ɑ�������
�@�@�@�@((X+ x0)/2-1)2+((Y+ y0)/2)2=1
�@�@�@�@((X+( x0-2))2+(Y+ y0)2=22�E�E�E�D
�i���a2�A���S�i2-x0,
-y0�j�̉~�ƂȂ�܂��B
�����ŁA�_P�̌Œ���������~�D�̒��S�̋O�Ղ��l���܂��B�i�������邱�Ƃɂ��_PQ�̎�肤��l�̂��ׂĂ�ԗ��ł��܂��j
�D�̒��S�̍��W���@���ɑ�����܂�
(2-x+1)2+�i-y�j2=1
(x-3)2+y2=1�E�E�E�E���B�f
���a1,���S�i3,0�j�̉~
�@�~�D�̔��a��2�Ȃ̂ŁAR�͒��S�̋O�Ձi�~�j�̓����̒l�͂Ƃ�܂���
�@����ɁA�~�D�̒��S�̋O�Ղ̒��S�́i3,0�j�Ȃ̂ʼn~�D�͉~�B�̓����ł������݂����܂���B
�@
�@����������R�̋O�Ղ̎�肦��l�̖ʐς�
��32-��8�E�E�E��
�@�@���݂ɁA�~�B�͉~�Q�C�̊O���̕���A�~�B�f�͓����̕���ƂȂ��Ă��܂��B
�@�@����̋��ߕ��́A45�N�O�Ɋw�͂��Ȃ̂ł����Y��Ă��܂��܂����̂Ŗ���������Ă݂܂����B
NO2�u���N���̂�������v 09/06 10��01���@��M 9/30
�u���N���̂�������v 09/06 21��21���@��M �X�V 9/30
���~A�AB�̒��S��x����ɂƂ�A���_�Ō݂��ɐڂ���悤�ɂ����܂��B
�~�̕������́A![]()
�e�_�̍��W���AP![]() �AQ
�AQ![]() �AR
�AR![]() �Ƃ��܂��B
�Ƃ��܂��B

����PR�̒��_��Q�Ȃ̂ŁA

����āA�~B�̕������ɓ���āA
![]()
![]()
�܂�A�_R�́A���S![]() �A���a2�̉~D�̎���ɂ���܂��B
�A���a2�̉~D�̎���ɂ���܂��B
���̉~D�̒��SS![]() �Ɠ_P
�Ɠ_P![]() �̒��_�́A
�̒��_�́A
![]()
���A�~B�̒��S�ł��B
�����ɓ_R������~D�̒��SS![]() ���ǂ��ɂ��邩���l���܂��B
���ǂ��ɂ��邩���l���܂��B
����PS�̒��_���~B�̒��S![]() �Ȃ̂ŁA
�Ȃ̂ŁA

����āA
![]()
������A�~A�̕������ɓ����ƁA
![]()
![]()
�~D�̒��SS![]() �́A���S
�́A���S![]() �A���a1�̉~C�̎���ɂ���܂��B
�A���a1�̉~C�̎���ɂ���܂��B
�~A�Ɖ~C�Ƃ́A�_![]() �Ɋւ��āA�Ώ̂ł��B
�Ɋւ��āA�Ώ̂ł��B
�����a2�̉~D���A���S���~C��ɒu���Ȃ��瓮�����Ƃ��l���܂��B
�~C�̒��S![]() ����~D��ň�ԉ����_�܂ł́A������3�ł��B�i�}�̓_T�j
����~D��ň�ԉ����_�܂ł́A������3�ł��B�i�}�̓_T�j
�~C�̒��S(3,0) ����~D��ň�ԋ߂��_�܂ł́A������1�ł��B�i�}�̓_U�j
�����_�́A���a3�̉~��`���܂��B
�߂��_�́A���a1�̉~��`���܂��B
���a1�̉~�̓����ɓ_R�͑��݂ł��܂���B
�܂�A���a3�̉~����A���a1�̉~������ʂ��悢�̂ŁA���߂�ʐς�9�|��8�ł��B
NO3�u�W���[�J�[�v �@
10/20 10��28���@��M �X�V 10/22

�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
