平成３０年１２月２３日

[流れ星]

　　　　第367回数学的な応募解答

　　　　＜解答募集期間：11月25日〜12月23日＞

［三角形の面積比］

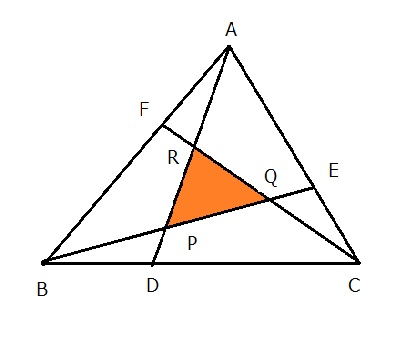
　△ＡＢＣの各頂点から、それぞれの対辺をｍ：ｎに分ける点をＤ，Ｅ，Ｆとし、直線ＡＤ，ＢＥ，ＣＦを引く。また、図で示した三角形をＰＱＲとする。

　ただし、ｍ≠ｎである。

問題１：ｍ＝１、ｎ＝２このとき、△ＡＢＣと△ＰＱＲの面積の比を求めよ。

問題２：△ＡＢＣと△ＰＱＲの面積の比をｍとｎで表せ。

NO1「早起きのおじさん」 11/28 17時32分　受信

「早起きのおじさん」 11/29 05時14分　受信 更新 12/23

367解答　早起きのおじさん

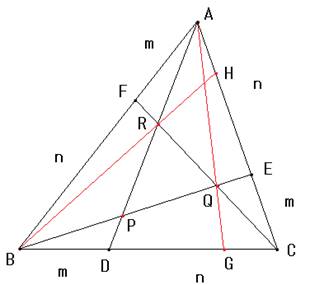
図は、m＜nの場合です。（m＞nのときも、同様に考えることができます）

図のように直線AGとBHを引きます。

△ABCの内部の点Qを通る3直線が三角形の各頂点を通るので、チェバの定理より、

よって、

△CFBを直線AGが通るので、メネラウスの定理より、

よって、

△CFBを直線ADが通るので、メネラウスの定理より、

よって、

以上から

ここで、文字のローテーションを考えます。

A→B→C→Aへ戻る、D→E→F→Dへ戻る、P→Q→R→Pへ戻る、G→H

このローテーションを上の枠内に行うと、

となります。

線分の長さの比は、次の図のようになります。

△ABCから△ADCは、底辺が(m+n)からnの割合になるので、

となります。

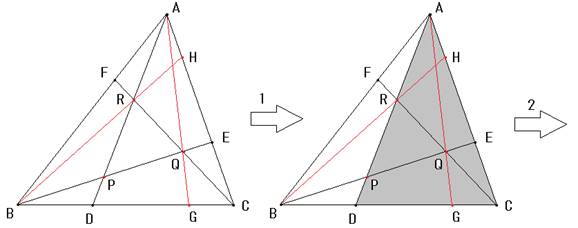
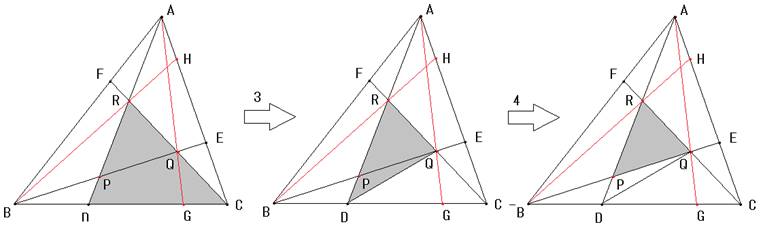
この要領で、辺の長さの比を考えて、△PQRまで考えます。

1番目は、上でみたように、

2番目は、同様に、

3番目は、同様に、

4番目は、同様に、

なので、

まとめると、

問題1は、m＝1、n＝2として、

△ABC：△PQR＝7：1

NO2「スモークマン」 12/08 00時41分　受信 更新 12/23

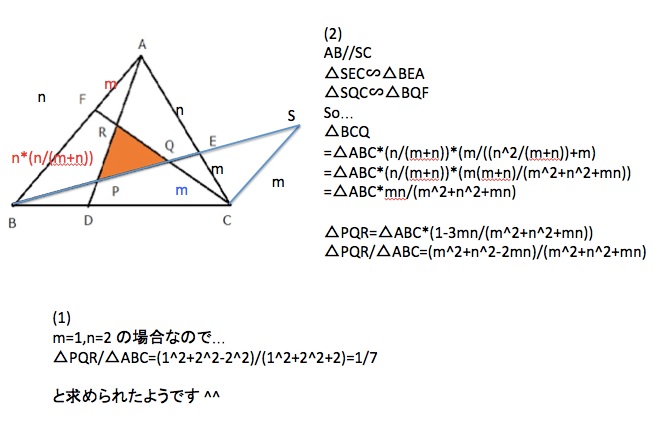
NO3「Kasama」 12/15 22時48分　受信 更新 12/23

補助線によってできた各三角形に着目すると、

＝

−＋

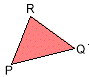
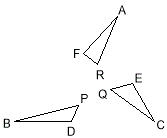
であることがわかります。数式で表現すれば、

　△PQR=△ABC - (△ABD+△BCE+△CAF) + △BDP+△CEQ+△AFR…�@

です。これらの三角形の面積を辺の比を使って計算し、△ABCと△PQRの面積比を求めます。

(1)△ABD、△BCE、△CAFの面積比の計算

点D、E、Fは辺BC、CA、ABの内分点なので、

　BD:CD=CD:AE=AF:BF=k:1-k(0＜k＜1)

と表すことができます。すると、△ABCと△ABD、△BCE、△CAFについて、辺の比から、

　△ABD=△BCE=△CAF=k×△ABC…�A

であることがわかります。

(2)△BDP、△CEQ、△AFRの面積比の計算

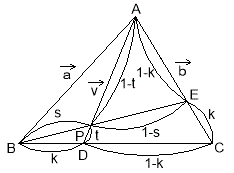右図のように、

=、=、=　　　

　BD:CD=CE:AE=k:1-k(0＜k＜1)

　BP:EP=s:1-s(0＜s＜1)

　DP:AP=t:1-t(0＜t＜1)

とします。

△ABEにおいて、

　=(1-s)+s(1-k)

また、△ABDにおいて、

　=(1-t){(1-k)+k}

です。両者は同じベクトルで、、は一次独立なので、それらの係数は等しく、

　1-s=(1-t)(1-k)

　s(1-k)=(1-t)k

これらを解いて、

　s=k/(k2-k+1)

　t=k2/(k2-k+1)

この比と�Aを使って、三角形の面積を求めると、

　△BDP=t×△ABD=t×k×△ABC=k3/(k2-k+1)×△ABC

です。△CEQ、△AFRについても同様なので、

　△BDP=△CEQ=△AFR=k3/(k2-k+1)×△ABC…�B

(3)△PQRの面積比の計算

�@に�A�Bを代入すると、

　△PQR={1-3k+3k3/(k2-k+1)}×△ABC=(2k-1)2/(k2-k+1)×△ABC

　⇒△PQR:△ABC=(2k-1)2:k2-k+1…�C

となります。

問題１

m:n=1:2=1/3:2/3なので、�C式にk=1/3を代入すると、

　△ABC:△PQR=25/49:43/49=7:1

です。

問題２

m:n=m/(m+n):n/(m+n)なので、�C式にk=m/(m+n)を代入すると、

　△ABC:△PQR={(n-m)/(n+m)}2/{(n2+mn+m2)/(n+m)2}=(n-m)2:n2+mn+m2

です。