�ߘa���N9��29��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��377�����w�I�ȉ����
�@�@�@�@����W���ԁF9��1���`�X��29����
�m���̖��n
�@
���P�Ɩ��Q�̋L��[x]�̓K�E�X�L���ŁCx���Ȃ��ő�̐�����\�����̂Ƃ���B
NO1�u�l�c�����v
09/02 09��34���@��M �X�V 9/29
���R
�@�^�������O���������|�P(���{��)�Q
�@�@�@�����O���������|�P(���Q�{�Q�����{���Q)
�@�@�@�����Q���O���������|�P�P�{�Q�����O���������|�P���{���O���������|�P���Q
�@�@�@�����Q���{�Q���E�P�^�Q�E(���|�P)���{�P�^�U�E(���|�P)��(�Q���|�P)
�@�@�@������(���{���|�P)�{(���|�P)��(�Q���|�P)�^�U
�@�@�@���P�X�U�S
�@�����̂悤��VBSCRIPT�ʼn������D
s=0
for k=1 to 2019
�@s=s+int(log(k)/log(2))
next
kotae="1:"&s
'
s=0
n=0
while 2019>s
�@n=n+1
�@s=s+int(log(n)/log(2))
�@if s=2018 then
�@�@k=n
�@end if
wend
kotae=kotae&chr(13)&"2:"&n
'
k=0
s=""
for a=0 to 1964
�@for n=0 to 1964
�@�@if a*n*(a+n-1)+(n-1)*n*(2*n-1)/6=1964 then
�@�@�@k=k+1
�@�@�@if k>1 then'�������������Ă��Ώ��ł���悤��
�@�@�@�@s=s&chr(13)&" "
�@�@�@end if
�@�@�@s=s&"a="&a&",n="&n
�@�@end if
�@next
next
kotae=kotae&chr(13)&"3:"&s
msgbox kotae
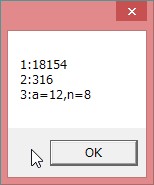
�@���R�̓��́C
�@�@�P�Q�Q�{�P�R�Q�{�P�S�Q�{�E�E�E�{�P�X�Q���P�X�U�S
�u�l�c�����v
09/04 12��37���@��M �X�V 9/29
���P
�@�@�����P�̂Ƃ��C[log�Q��]���O
�@�@�Q�P�������Q�Q�̂Ƃ��C[log�Q��]���P
�@�@�Q�Q�������Q�R�̂Ƃ��C[log�Q��]���Q
�@�@�Q�R�������Q�S�̂Ƃ��C[log�Q��]���R
�@�@�E�E�E
�@�@�Q���������Q���{�P�̂Ƃ��C[log�Q��]�����i���͐������j
�ł��邩��C
�@�@���P�������Q�O�P�X[log�Q��]�����P�������Q�O�S�V[log�Q��]�|���Q�O�Q�O�������Q�O�S�V[log�Q��]
�@�@�@��(�P�E�Q�P�{�Q�E�Q�Q�{�R�E�Q�R�{�E�E�E�{�P�O�E�Q�P�O)�|�P�O�E�Q�W
�@�����ŁC�r�����P�E�Q�P�{�Q�E�Q�Q�{�R�E�Q�R�{�E�E�E�{���E�Q���i���͐������j�Ƃ���ƁC
�@�@�@�r�����P�E�Q�P�{�Q�E�Q�Q�{�R�E�Q�R�{�E�E�E�{���E�Q��
�@�@�Q�r�����@�@�@�@�@�P�E�Q�Q�{�Q�E�Q�R�{�E�E�E�{(���|�P)�E�Q���{���E�Q���{�P
�@�����Ƃ�ƁC
�@�@�|�r�����Q�P�{�Q�Q�{�Q�R�{�E�E�E�{�Q���|���E�Q���{�P
�@�@�@�@�@���Q(�Q���|�P)�^(�Q�|�P)�|���E�Q���{�P
�@�@�@�@�@��(�P�|��)�Q���{�P�|�Q
�@�@���r����(���|�P)�Q���{�P�{�Q
�@�@���r�P�O���X�E�Q�P�P�{�Q���P�W�S�R�S
�@�@���^�����P�W�S�R�S�|�Q�W�O���P�W�P�T�S�E�E�E�i���j
���Q
�@�r�����Q�O�P�W���r���{�P�i���͐������j�Ƃ���ƁC�r����(���|�P)�E�Q���{�P�{�Q���C
�@�@(���|�P)�E�Q���{�P���Q�O�P�U�����E�Q���{�Q
�@��(��)��(���|�P)�E�Q���{�P�Ƃ���ƁC�����P�ŁC��(��)�͒P���������ł���C
�@�@��(�V)���P�T�R�U�C��(�W)���R�T�W�S
����C��(�V)���Q�O�P�U����(�W)
�@�r�V���P�T�R�W���Q�O�P�W�|�S�W�O���Q�O�P�W�|�W�E�U�O�Ȃ̂ŁC
�@�@�����Q�W�{�U�O���Q�T�U�{�U�O���R�P�U�E�E�E�i���j
���R
�@����(���{���|�P)�{(���|�P)��(�Q���|�P)�^�U���P�X�U�S���C
�@�@����(���{���|�P)���P�X�U�S�|(���|�P)��(�Q���|�P)�^�U���O
�@�@��(���|�P)��(�Q���|�P)�^�U���P�X�U�S
�@��(��)��(���|�P)��(�Q���|�P)�^�U�Ƃ���ƁC�����P���C��(��)�͒P��������
�@��(�P�W)���P�V�W�T�C��(�P�X)���Q�P�O�X�Ȃ̂ŁC
�@�@�����P�W
i). �����P�̂Ƃ��C���Q���P�X�U�S���Q�Q�E�S�X�P
�@�S�X�P�͑f���Ȃ̂ŁC���͐����ɂȂ�Ȃ��D
ii). �����Q�̂Ƃ��C�Q��(���{�P)���P�X�U�S�|�P
�@(����)��(�)�ƂȂ�̂ŁC��������D
iii). �����R�̂Ƃ��C�R��(���{�Q)���P�X�U�S�|�T���P�X�T�X
�@�@����(���{�Q)���U�T�R�i�f���j
�@��������������͑��݂��Ȃ��D
iv). �����S�̂Ƃ��C�S��(���{�R)���P�X�U�S�|�Q�E�V
�@�@���Q��(���{�R)���X�W�Q�|�V
�@(����)��(�)�ƂȂ�̂ŁC��������D
v). �����T�̂Ƃ��C�T��(���{�S)���P�X�U�S�|�Q�E�T�E�R
�@�@���T{��(���{�S)�{�Q�E�R}���P�X�U�S
�@�E�ӂ͂T�̔{���ł͂Ȃ��̂ŁC��������D
vi). �����U�̂Ƃ��C�U��(���{�T)���P�X�U�S�|�T�E�P�P
�@(����)��(�)�ƂȂ�̂ŁC��������D
vii). �����V�̂Ƃ��C�V��(���{�U)���P�X�U�S�|�V�E�P�R
�@�@���V{��(���{�U)�{�P�R}���Q�Q�E�S�X�P
�@�E�ӂ͂V�̔{���ł͂Ȃ��̂ŁC��������D
viii). �����W�̂Ƃ��C�W��(���{�V)���P�X�U�S�|�V�E�S�E�T
�@�@���Q��(���{�V)���S�X�P�|�V�E�T���S�T�U
�@�@����(���{�V)���Q�Q�W���P�Q�E�P�X
�@�����O�Ȃ̂ŁC��(���{�V)�́C���̒P��������
�@�@�������P�Q
ix). �����X�̂Ƃ��C�X��(���{�W)���P�X�U�S�|�S�E�R�E�P�V
�@�@���R{�R��(���{�W)�{�S�E�P�V}���Q�Q�E�S�X�P
�@�E�ӂ͂R�̔{���ł͂Ȃ��̂ŁC��������D
x). �����P�O�̂Ƃ��C�P�O��(���{�X)���P�X�U�S�|�R�E�T�E�P�X
�@�@���T{�Q��(���{�X)�{�R�E�P�X}���P�X�U�S
�@�E�ӂ͂T�̔{���ł͂Ȃ��̂ŁC��������D
xi). �����P�P�̂Ƃ��C�P�P��(���{�P�O)���P�X�U�S�|�T�E�P�P�E�V
�@�@���P�P{��(���{�P�O)�{�T�E�V}���Q�Q�E�S�X�P
�@�E�ӂ͂P�P�̔{���ł͂Ȃ��̂ŁC��������D
xii). �����P�Q�̂Ƃ��C�P�Q��(���{�P�P)���P�X�U�S�|�P�P�E�Q�E�Q�R
�@�@���U��(���{�P�P)���X�W�Q�|�P�P�E�Q�R
�@(����)��(�)�ƂȂ�̂ŁC��������D
xiii). �����P�R�̂Ƃ��C�P�R��(���{�P�Q)���P�X�U�S�|�Q�E�P�R�E�Q�T
�@�@���P�R{��(���{�P�Q)�{�Q�E�Q�T}���Q�Q�E�S�X�P
�@�E�ӂ͂P�R�̔{���ł͂Ȃ��̂ŁC��������D
xiv). �����P�S�̂Ƃ��C�P�S��(���{�P�R)���P�X�U�S�|�P�R�E�V�E�X
�@�@���V{�Q��(���{�P�R)�{�P�R�E�X}���Q�Q�E�S�X�P
�@�E�ӂ͂V�̔{���ł͂Ȃ��̂ŁC��������D
xv). �����P�T�̂Ƃ��C�P�T��(���{�P�S)���P�X�U�S�|�V�E�T�E�Q�X
�@�@���T{�R��(���{�P�S)�{�V�E�Q�X}���P�X�U�S
�@�E�ӂ͂T�̔{���ł͂Ȃ��̂ŁC��������D
xvi). �����P�U�̂Ƃ��C�P�U��(���{�P�T)���P�X�U�S�|�T�E�W�E�R�P
�@�@���S��(���{�P�T)���S�X�P�|�T�E�Q�E�R�P
�@(����)��(�)�ƂȂ�̂ŁC��������D
xvii). �����P�V�̂Ƃ��C�P�V��(���{�P�U)���P�X�U�S�|�W�E�P�V�E�P�P
�@�@���P�V{��(���{�P�U)�{�W�E�P�P}���Q�Q�E�S�X�P
�@�E�ӂ͂P�V�̔{���ł͂Ȃ��̂ŁC��������D
xviii). �����P�W�̂Ƃ��C�P�W��(���{�P�V)���P�X�U�S�|�P�V�E�R�E�R�T
�@(����)��(�)�ƂȂ�̂ŁC��������D
�@�ȏ���C(���C��)��(�P�Q�C�W)
�u�l�c�����v
09/05 10��55���@��M �X�V 9/29
���R
�@�^�������O���������|�P(���{��)�Q
�@�@�@�����O���������|�P(���Q�{�Q�����{���Q)
�@�@�@�����Q���O���������|�P�P�{�Q�����O���������|�P���{���O���������|�P���Q
�@�@�@�����Q���{�Q���E�P�^�Q�E(���|�P)���{�P�^�U�E(���|�P)��(�Q���|�P)
�@�@�@������(���{���|�P)�{(���|�P)��(�Q���|�P)�^�U
�@�@�@���P�X�U�S
�@�����̂悤��VBSCRIPT�ʼn������D
s=0
for k=1 to 2019
�@s=s+int(log(k)/log(2))
next
kotae="1:"&s
'
s=0
n=0
while 2018>s
�@n=n+1
�@s=s+int(log(n)/log(2))
wend
kotae=kotae&chr(13)&"2:"&n
'
k=0
s=""
for a=0 to 1964
�@for n=0 to 1964
�@�@if a*n*(a+n-1)+(n-1)*n*(2*n-1)/6=1964 then
�@�@�@k=k+1
�@�@�@if k>1 then'�������������Ă��Ώ��ł���悤��
�@�@�@�@s=s&chr(13)&" "
�@�@�@end if
�@�@�@s=s&"a="&a&",n="&n
�@�@end if
�@next
next
kotae=kotae&chr(13)&"3:"&s
msgbox kotae
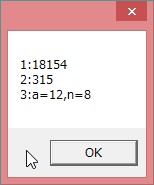
�@���R�̓��́C
�@�@�P�Q�Q�{�P�R�Q�{�P�S�Q�{�E�E�E�{�P�X�Q���P�X�U�S
�i�ʉ��j
���P
�@�@�����P�̂Ƃ��C[log�Q��]���O
�@�@�Q�P�������Q�Q�̂Ƃ��C[log�Q��]���P
�@�@�Q�Q�������Q�R�̂Ƃ��C[log�Q��]���Q
�@�@�Q�R�������Q�S�̂Ƃ��C[log�Q��]���R
�@�@�E�E�E
�@�@�Q���������Q���{�P�̂Ƃ��C[log�Q��]�����i���͐������j
�ł��邩��C
�@�@���P�������Q�O�P�X[log�Q��]�����P�������Q�O�S�V[log�Q��]�|���Q�O�Q�O�������Q�O�S�V[log�Q��]
�@�@�@��(�P�E�Q�P�{�Q�E�Q�Q�{�R�E�Q�R�{�E�E�E�{�P�O�E�Q�P�O)�|�P�O�E�Q�W
�@�����ŁC�r�����P�E�Q�P�{�Q�E�Q�Q�{�R�E�Q�R�{�E�E�E�{���E�Q���i���͐������j�Ƃ���ƁC
�@�@�@�r�����P�E�Q�P�{�Q�E�Q�Q�{�R�E�Q�R�{�E�E�E�{���E�Q��
�@�@�Q�r�����@�@�@�@�@�P�E�Q�Q�{�Q�E�Q�R�{�E�E�E�{(���|�P)�E�Q���{���E�Q���{�P
�@�����Ƃ�ƁC
�@�@�|�r�����Q�P�{�Q�Q�{�Q�R�{�E�E�E�{�Q���|���E�Q���{�P
�@�@�@�@�@���Q(�Q���|�P)�^(�Q�|�P)�|���E�Q���{�P
�@�@�@�@�@��(�P�|��)�Q���{�P�|�Q
�@�@���r����(���|�P)�Q���{�P�{�Q
�@�@���r�P�O���X�E�Q�P�P�{�Q���P�W�S�R�S
�@�@���^�����P�W�S�R�S�|�Q�W�O���P�W�P�T�S�E�E�E�i���j
���Q
�@�r�����Q�O�P�W���r���{�P�i���͐������j�Ƃ���ƁC�r����(���|�P)�E�Q���{�P�{�Q���C
�@�@(���|�P)�E�Q���{�P���Q�O�P�U�����E�Q���{�Q
�@��(��)��(���|�P)�E�Q���{�P�Ƃ���ƁC�����P�ŁC��(��)�͒P���������ł���C
�@�@��(�V)���P�T�R�U�C��(�W)���R�T�W�S
����C��(�V)���Q�O�P�U����(�W)
�@�r�V���P�T�R�W���Q�O�P�W�|�S�W�O���Q�O�P�W�|�W�E�U�O�Ȃ̂ŁC
�@�@�����Q�W�{(�U�O�|�P)���Q�T�U�{�T�X���R�P�T�E�E�E�i���j
���R
�@����(���{���|�P)�{(���|�P)��(�Q���|�P)�^�U���P�X�U�S���C
�@�@����(���{���|�P)���P�X�U�S�|(���|�P)��(�Q���|�P)�^�U���O
�@�@��(���|�P)��(�Q���|�P)�^�U���P�X�U�S
�@��(��)��(���|�P)��(�Q���|�P)�^�U�Ƃ���ƁC�����P���C��(��)�͒P��������
�@��(�P�W)���P�V�W�T�C��(�P�X)���Q�P�O�X�Ȃ̂ŁC
�@�@�����P�W
i). �����P�̂Ƃ��C���Q���P�X�U�S���Q�Q�E�S�X�P
�@�S�X�P�͑f���Ȃ̂ŁC���͐����ɂȂ�Ȃ��D
ii). �����Q�̂Ƃ��C�Q��(���{�P)���P�X�U�S�|�P
�@(����)��(�)�ƂȂ�̂ŁC��������D
iii). �����R�̂Ƃ��C�R��(���{�Q)���P�X�U�S�|�T���P�X�T�X
�@�@����(���{�Q)���U�T�R�i�f���j
�@��������������͑��݂��Ȃ��D
iv). �����S�̂Ƃ��C�S��(���{�R)���P�X�U�S�|�Q�E�V
�@�@���Q��(���{�R)���X�W�Q�|�V
�@(����)��(�)�ƂȂ�̂ŁC��������D
v). �����T�̂Ƃ��C�T��(���{�S)���P�X�U�S�|�Q�E�T�E�R
�@�@���T{��(���{�S)�{�Q�E�R}���P�X�U�S
�@�E�ӂ͂T�̔{���ł͂Ȃ��̂ŁC��������D
vi). �����U�̂Ƃ��C�U��(���{�T)���P�X�U�S�|�T�E�P�P
�@(����)��(�)�ƂȂ�̂ŁC��������D
vii). �����V�̂Ƃ��C�V��(���{�U)���P�X�U�S�|�V�E�P�R
�@�@���V{��(���{�U)�{�P�R}���Q�Q�E�S�X�P
�@�E�ӂ͂V�̔{���ł͂Ȃ��̂ŁC��������D
viii). �����W�̂Ƃ��C�W��(���{�V)���P�X�U�S�|�V�E�S�E�T
�@�@���Q��(���{�V)���S�X�P�|�V�E�T���S�T�U
�@�@����(���{�V)���Q�Q�W���P�Q�E�P�X
�@�����O�Ȃ̂ŁC��(���{�V)�́C���̒P��������
�@�@�������P�Q
ix). �����X�̂Ƃ��C�X��(���{�W)���P�X�U�S�|�S�E�R�E�P�V
�@�@���R{�R��(���{�W)�{�S�E�P�V}���Q�Q�E�S�X�P
�@�E�ӂ͂R�̔{���ł͂Ȃ��̂ŁC��������D
x). �����P�O�̂Ƃ��C�P�O��(���{�X)���P�X�U�S�|�R�E�T�E�P�X
�@�@���T{�Q��(���{�X)�{�R�E�P�X}���P�X�U�S
�@�E�ӂ͂T�̔{���ł͂Ȃ��̂ŁC��������D
xi). �����P�P�̂Ƃ��C�P�P��(���{�P�O)���P�X�U�S�|�T�E�P�P�E�V
�@�@���P�P{��(���{�P�O)�{�T�E�V}���Q�Q�E�S�X�P
�@�E�ӂ͂P�P�̔{���ł͂Ȃ��̂ŁC��������D
xii). �����P�Q�̂Ƃ��C�P�Q��(���{�P�P)���P�X�U�S�|�P�P�E�Q�E�Q�R
�@�@���U��(���{�P�P)���X�W�Q�|�P�P�E�Q�R
�@(����)��(�)�ƂȂ�̂ŁC��������D
xiii). �����P�R�̂Ƃ��C�P�R��(���{�P�Q)���P�X�U�S�|�Q�E�P�R�E�Q�T
�@�@���P�R{��(���{�P�Q)�{�Q�E�Q�T}���Q�Q�E�S�X�P
�@�E�ӂ͂P�R�̔{���ł͂Ȃ��̂ŁC��������D
xiv). �����P�S�̂Ƃ��C�P�S��(���{�P�R)���P�X�U�S�|�P�R�E�V�E�X
�@�@���V{�Q��(���{�P�R)�{�P�R�E�X}���Q�Q�E�S�X�P
�@�E�ӂ͂V�̔{���ł͂Ȃ��̂ŁC��������D
xv). �����P�T�̂Ƃ��C�P�T��(���{�P�S)���P�X�U�S�|�V�E�T�E�Q�X
�@�@���T{�R��(���{�P�S)�{�V�E�Q�X}���P�X�U�S
�@�E�ӂ͂T�̔{���ł͂Ȃ��̂ŁC��������D
xvi). �����P�U�̂Ƃ��C�P�U��(���{�P�T)���P�X�U�S�|�T�E�W�E�R�P
�@�@���S��(���{�P�T)���S�X�P�|�T�E�Q�E�R�P
�@(����)��(�)�ƂȂ�̂ŁC��������D
xvii). �����P�V�̂Ƃ��C�P�V��(���{�P�U)���P�X�U�S�|�W�E�P�V�E�P�P
�@�@���P�V{��(���{�P�U)�{�W�E�P�P}���Q�Q�E�S�X�P
�@�E�ӂ͂P�V�̔{���ł͂Ȃ��̂ŁC��������D
xviii). �����P�W�̂Ƃ��C�P�W��(���{�P�V)���P�X�U�S�|�P�V�E�R�E�R�T
�@(����)��(�)�ƂȂ�̂ŁC��������D
�@�ȏ���C(���C��)��(�P�Q�C�W)
�@�E�E�E
���R�i�Q�l�j
�@�@����(���{���|�P)���P�X�U�S�|(���|�P)��(�Q���|�P)�^�U���P�X�U�S�E�E�E(1)
�@���O���������|�P���Q��(���|�P)��(�Q���|�P)�^�U�ł��邩��C
�@�@�����P�C�S�C�T�C�W�C�X�C�P�Q�C�P�R�C�P�U�C�P�V
�̂Ƃ��C(1)�̉E�ӂ͋����C
�@�@�����Q�C�R�C�U�C�V�C�P�O�C�P�P�C�P�S�C�P�T�C�P�W
�̂Ƃ��C(1)�̉E�ӂ͊�D
�@���������̂Ƃ��C(1)�̍��ӂ͋����Ȃ̂ŁC�����P�W�͈̔͂ł́C
�@�@�����Q�C�U�C�P�O�C�P�S�C�P�W
�̂Ƃ��C(1)�͕s�����D
�@�̂ɂP�V�ȉ��̑��̐������ōl����悢�D
�@�������C���̂P�R�̒l�Ōv�Z���Ă��C���X�̂P�W�̒l�Ōv�Z���Ă�����Ȃɕς��Ȃ��C������D
�@���ɂ����ƌ����I�ȉ�����������Εʂł��邪�D
NO2�u�X���[�N�}���v 09/02 23��51���@��M
�X�V 9/29
(1)
[log(2)1]+[log(2)2]+...+[log(2)2019]
1...0
2〜3...1
4〜7...2
...
2^9〜2^10-1=1023...9
2^10=1024〜2019...10
so...
1*2+2*4+3*8+4*16+5*32+6*64+7*128+8*256+9*512+�{10*(2019-1023)
=18154
(2)
1*2+2*4+3*8+4*16+5*32+6*64+7*128=1538
2018-1538=480
480/8=60
so...
�Q�O�W�{�U�O�|�P=315=n
(3)
�q���g���...
n(6a^2+6a(n-1)+(n-1)(2n-1))=6*1964
6*1964=2^4*3*491
n����ł�...1 or 3 or
491�Ŗ��������̂��Ȃ�...
n=2,4,6,8,12,24��...
�Ђ�����v�Z������...
n=8,a=12�܂���...^^
so...
12^2+13^2+14^2+�E�E�E+19�O2
���ۂ�...
(19*20*39-11*12*23)/6=1964 ��
���������̂��āA���܂����@���Ă���̂ł��傤�������...?
NO3�u���N���̂�������v 09/09 17��03���@��M �X�V 9/29
377�@���N���̂�������
���1

��̕\���A
![]()
��������S�Ƃ����ƁA
![]()
![]()
![]()
![]()
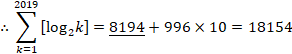
���2
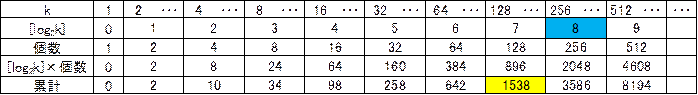
��̕\���A
![]()
![]()
���3
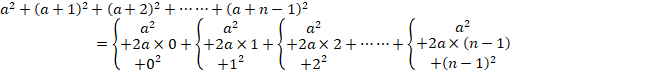

![]()
����āA
![]()
���̎���10�i�@��11784�ƕ\����鐔��n�i�@�ł�(2)(6a�|3)(6a2�|6a�{1)(0)�ƂȂ�ƍl���܂��B
(��������4���ł�)
a�Ő�������Ɓu1�v�̈ʂ�(0)�łȂ��̂ŏꍇ�̐��������܂��B
11784��f������������ƁA
![]()
�܂�A11784�̖o2�A4�A8�A3�A6�A12�A24�A����p�Ȃǂ̐i�@���l����悢�킯�ł��B
 �Ⴆ�A12�i�@�ŕ\���ƉE�̌v�Z���A
�Ⴆ�A12�i�@�ŕ\���ƉE�̌v�Z���A
![]()
��4���ɂȂ�܂��B
��̌v�Z�ł́An��3��̌���2�Ȃ̂ŁA
![]()
![]()
��(1)���݂�ƁAn2�̈ʂ��n�̈ʂ̐����̕����傫���̂ŁAm����n�̈ʂɈڂ��܂��B
����ƁA
![]()
��̎����Am��60�|6a
���̎��ɓ���āA
![]()
![]()
![]()
a�͐��Ȃ̂ŁA
![]()
a�������ɂȂ�Ȃ��̂ł��̕��j�ł̉��͂���܂���B
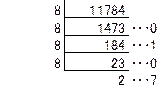 ���ɁA�Ⴆ��8�i�@�ŕ\���ƉE�̌v�Z���A
���ɁA�Ⴆ��8�i�@�ŕ\���ƉE�̌v�Z���A
![]()
��5���ɂȂ��Ă��܂��܂��B
��̌v�Z�ł́An��3��̌���2�Ȃ̂ŁA
![]()
![]()
![]()
��(1)���݂�ƁAn2�̈ʂ��n�̈ʂ̐����̕����傫���̂ŁAm����n�̈ʂɈڂ��܂��B
����ƁA
![]()
��̎����Am��171�|6a
���̎��ɓ���āA
![]()
![]()
![]()
a�͐��Ȃ̂ŁA
![]()
�ȏォ��An��8�Aa��12
NO4�u��x�Ђ����v 09/14 15��26���@��M
�X�V 9/29
�y���l�[���F��x�Ђ�����
[���1]
floor(log{2}k)=n �� n��log{2}k��n+1 �� 2^n��k��2^(n+1)�D
2^10��2019��2^11�D
����āC
��[k=1�`2019]floor(log{2}k)
=��[n=0�`9]n*(2^(n+1)-2^n)
+ 10*(2019-2^10+1)
=8194+9960
=18154 (��)
[���2]
��[k=0�`7]k*(2^(k+1)-2^k)=1538�C
��[k=0�`8]k*(2^(k+1)-2^k)=3586�D
1538 + 8*(n - 2^8
+ 1) = 2018 �������āC
n=315(��)
[���3]
��[k=0�`n-1](a+k)^2=1964
�����悤�Ȏ��R�� a�Cn �����߂�悢�D
��[k=0�`n-1](a+k)^2=1964
��
n*(a^2+(n-1)*a+(n-1)*(2*n-1)/6)=1964
��
n*(6*a^2+6*(n-1)*a+(n-1)*(2*n-1))=2^3*3*491 --- (��)
1964�͕������ł͂Ȃ�����C2��n�D
�܂��C��[k=0�`18-1](1+k)^2 = 2109 �� 1964 ���Cn��17�D
����āC2��n��17--- (����)�D
�����������ɕ��ׁC������4�Ŋ������]��ɒ��ڂ���ƁC
1��0�����݂ɌJ��Ԃ��o������D
1964��4�̔{���ł��邱�Ƃ��l����Cn�̕�����
a^2�C(a+1)^2�C�c�C(a+n-1)^2
�̒��ɂ́C4�Ŋ������]�肪 1 �ƂȂ�悤�Ȃ��̂�
4�̔{����������D
����ƁC(��)�����(����)�Ƃ���Cn�̒l�Ƃ��ĉ\��
�̂�����̂́Ca�̒l�ɂ�����炸�Cn=8 �̂݁D
����ɁCn=8 �̂Ƃ���(��)���� ���R�� a �͑��݂���D
(��)�ɂ����� n=8 ��������� a=12 ��D
���͎��̂悤�ɂȂ�D
12^2+13^2+14^2+15^2+16^2+17^2+18^2+19^2
= 1964�D
�ȏ�
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
