令和２年３月１５日

[流れ星]

　　　　第384回数学的な応募問題

　　　　＜解答募集期間：3月15日〜4月12日＞

［南宮大社奉納算額１］

江戸時代後期の和算家谷松茂（1800〜1841）がいました。諱は松茂、通称は次郎八、字は士好、号は幽斎。代々美濃国大垣城下で印刷彫刻を業とし、屋号は版木屋、父は良八。　　　

彼は和算を大垣藩の儒者水野民興らに学び、当時全国的に著名な和算家で名古屋の北川猛虎に弟子入りをしている。また、自らも大垣で和算塾を開き算法・算術を多く人に教えている。さらに、和算家谷幽斎は数学の問題を算額として神社等に掲げている。著作に「綴術新意」「幽斎算約初編」などがある。彼が1841年に亡くなったとき門弟が美濃国南宮大社に1842年奉献算額12題を残しました。でも、残念ながら算額は現存していません。そこで、皆さんの力を借りで、解法を現代に伝えたく、出題しました。

　第384回から3回続きます。

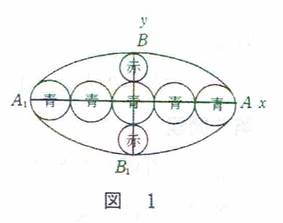
第１問題　楕円内に赤円二個と最も多くの青等円を入れる。赤円２個と青円一個との直径の和は短径に等しい。青円三個から初めて逐次偶数個を増すとする。赤円径と青円径をそれぞれ知って青等円の個数を求めよ。

第２問題　多角形（辺数は無関係、ここで仮に五角形とする）の内へ赤円を入れる。互いに外接する３個の青円は甲辺に接し、乙辺に接するように青等円数個を互いに外接させる。甲辺、乙辺の長さをそれぞれ知って青等円の個数を求めよ。

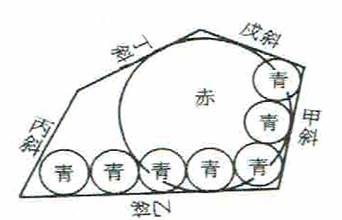
参考図

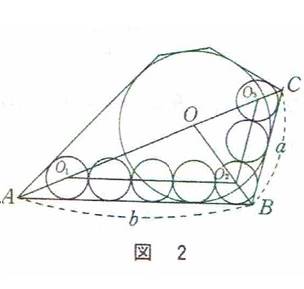
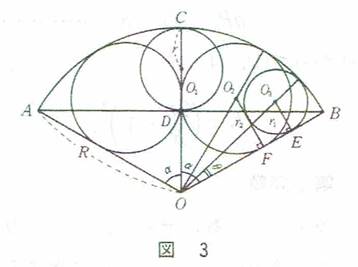
第３問題　扇面内に直線を引き黄円一個、青円二個（黄円の直径の４÷３を青円の直径とする）と赤円（等円）数個（仮に七個）を入れる。青円、赤円の直径を知って赤等円の個数を求めよ。

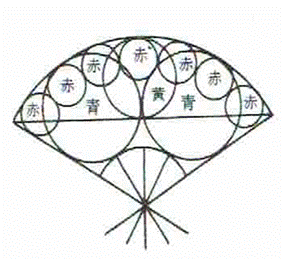
参考図

＜水の流れ　訂正のお詫び　答えの（Ａ）ですが、「早起きおじさん」から指摘があり、４/３の分数を１/３にしてください。3月31日夜記＞

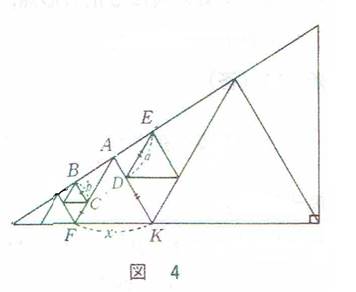
第４問題　直角三角形の内へ、異なる五個の正三角形を入れる。赤、黒の一辺の長さをそれぞれ知って白の一辺の長さを求めよ

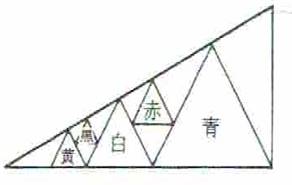
参考図

出典　岐阜県の算額の解説　��木重之　著　自費出版　

　

追加問題　出題者「ジョーカー」さん

＜水の流れ：綺麗な算額風の問題です＞

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。