�ߘa�V�N�R���Q��
 [���ꐯ]
[���ꐯ]
�@�@��452�����w�I�ȘA��������
�@�@�@����W���ԁF�R���Q���`�R���R�O����
�m�P�ʕ����n
�@���q���P�̕�����P�ʕ����Ƃ����A�������قȂ�P�ʕ����̘a�ŕ\�����Ƃ��P�ʕ��������Ƃ����B
���́A�P�ʕ��������̕��@�͖����ʂ肠��A�ؖ����邱�Ƃ��\�ł��B
��q�ɂ���Q�l���Q�Ƃ��������B
�P�ʕ��������̕��@�́A2�ʂ肠��܂��B
�P�@������������������A�ő�̒P�ʕ������Ђ��Ă������@
�Q�@�s�����ɂ���āA����ɂ��Ă͂܂鎩�R�������ڂ��Ă������@
�P�ʕ��������̕��@�P
�@�@���Ƃ̕�������A�����菬�����ő�̒P�ʕ������Ђ��B
�A�@���̌��ʂ��P�ʕ����Ȃ�I���B�P�ʕ����łȂ��Ȃ�A���̕�����菬�����ő�̒P�ʕ������Ђ��B
�B�@�A���J��Ԃ��B
���@�L����̌v�Z�ŕK���P�ʕ������o�ꂷ��B
��@ ![]() �̒P�ʕ�������
�̒P�ʕ�������
�@�@![]()
![]() �@��菬�����ő�̒P�ʕ����́A
�@��菬�����ő�̒P�ʕ����́A ![]() �@�Ȃ̂ŁA
�@�Ȃ̂ŁA
![]() ���@
���@![]()
�A�@ ![]() �͒P�ʕ����̂��߁A�����I���B
�͒P�ʕ����̂��߁A�����I���B
�P�ʕ��������̕��@�Q
�@�@���Ƃ̕��� ![]() (x<y) �Ƃ����B
(x<y) �Ƃ����B
�A�@x �ɂ��Ă͂܂�\���̂��鎩�R�������߂�B
�B�@ x �����ꂼ�������A���̂Ƃ���y �̒l�����R���i![]() ���P�ʕ���)�Ȃ�I�����A�����łȂ�����̕����ɂ���(1)���瓯����Ƃ��s���Ă����B
���P�ʕ���)�Ȃ�I�����A�����łȂ�����̕����ɂ���(1)���瓯����Ƃ��s���Ă����B
�� x �ɂ��Ă͂܂�\���̂��鎩�R���́An ���傫���A2n ��菬���������ƂȂ�܂��B
�����ŁA���ł�
���@![]() �̂悤�ɂR�̒P�ʕ����ɕ����ł��܂��B
�̂悤�ɂR�̒P�ʕ����ɕ����ł��܂��B
�P���S���P�ʕ����ɕ������Ă��������B
�]�͖��@�P���T�̈قȂ��P�ʕ����ɕ�������ƁB���g�ɂȂ�܂����B
���̏�ŁA����������ɂ́A�����Ȏ��Ԃ�������A�r���Œ��߂܂����B�@
�N���APC�ŋ��߂Ē����܂��B
�@�@�@�@�@�@
�Q�l�����@BLUEBACKS�@��w�Ō�鐔�_�̐��E�@��������@�u�k��
�Q�l��


�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y11,12���
�@����ŏI���ł��B
���1
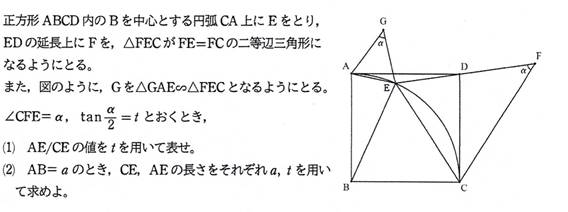
���Q
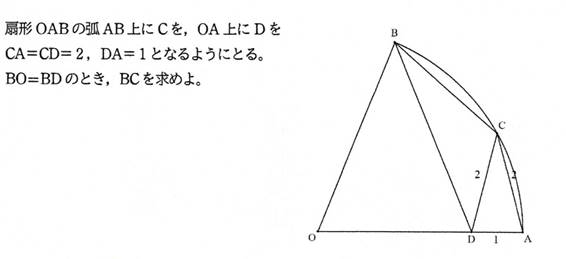
�@
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���, �ƃy���l�[����Y����, ���[���ő����Ă��������B�҂��Ă��܂��B
