令和８年１月４日

[流れ星]

　　第463回数学的な連続応募問題

　　　＜解答募集期間：１月４日〜２月１日＞

［2026の雑題(1)］
令和８年丙午（ひのえうま）明けましておめでとうございます。

昨年までのご応募に深く感謝申し上げます。

今年も引き続きご愛顧賜りますようよろしくお願いいたします。

問題１　

（１）ｘ^８−ｘ＋１　を因数分解せよ。

（２）2026⁸−2025は素数か合成数か判定せよ。

ヒント　−１の3乗根

問題２　ｘ^２＋２ｘ＋４＝０の解をα,βとするとき,

（１）α^ｎ＋β^ｎをｎで表せ。

（２）｜α²⁰²⁶＋β²⁰²⁶｜を31で割った余りを求めよ。

ヒント　８の3乗根

問題３　

（１）2026を自然数の3乗和で表し,その個数を6個以内でできるだけ見つけてください。　　　　　

（２）（１）で見つけたなかで、2026²⁰²⁶をできるだけ少ない個数の自然数の３乗和でひとつ表せ。

補足　（１）は数学ソフトで見つけても可

追加問題（出題者は「ジョーカー」）　新作シリーズ

四分円内の正方形と正三角形の1辺について『３』　

問題１　　シリーズ5問目

正方形と正三角形の1辺が異なる（ａ＞ｂ),

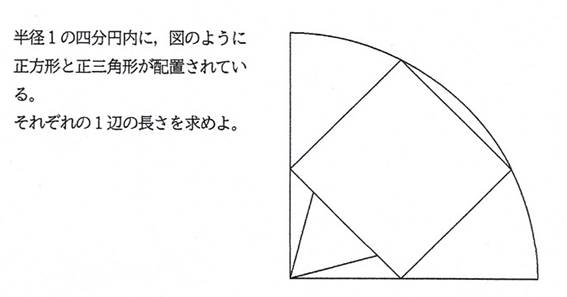
問題２　シリーズ6問目

正方形と正三角形の1辺が異なる（ａ＞ｂ),

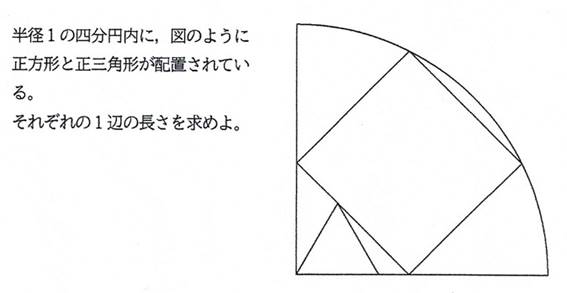
皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。