�����P�T�N�V���U��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@�@�@�@��P�Q�P�����w�I�ȉ������
�@�@�@�@�@�@�@�@�@�@����W���ԁF�U���P�T���`�V���U����
�m�T�捪�E�P�O�捪�n
�@�@�@
����́A�P�̂T�捪��P�O�捪�ɊW�̐[���R�p���̐ς̖��ł��B

�m�n�P�uH7K�v���� 6/16: 23��04�� ��M �@�X�V�V���U��
���܂��Ɂu�s���s�b�h���Q�v�͉����ł��Ă��܂���C�Ƃ������C���Ԃ��Ȃ��Ă��܂�l�����Ȃ������̂ł���...
���āC��121��ł����C��܂��ɂ͎��̊����ł��D
(1) sin 5x=sin(2x+3x)=...(�v�Z��)=16sin^5 x-20sin^3 x+5sin x
sin 5x=0�Ȃ�0<=x<2 pi��k*pi/5(k=0...9)�����C�����sin x���Ƃ��Ă݂�ƒl��0,+- sin pi/5,+-
sin 2pi/5��5��C
����āC����0,+- sin pi/5,+- sin 2pi/5��16x^2-20x^3+5x=0�̉��C
���ƌW���̊W���C5/16=sin pi/5 * -sin pi/5 * sin 2pi/5 * -sin 2pi/5=sin^2 pi/5 * sin^2
2pi/5...(1).
�����ŁCsin 4pi/5=sin pi/5�Csin 3pi/5=sin 2pi/5���Csin pi/5 * sin 2pi/5 * sin 3pi/5 *
sin 4pi/5=5/16.
(2) cos x=sin x+pi/2�����p����ƁC���ǂ��̎��͗e�Ղ�sin pi/5 * sin
2pi/5 * sin 3pi/5 * sin 4pi/5�ɕό`�ł���̂ŁC���R�l��5/16.
�m�n�Q�uKashiwagi�v���� 6/17: 08��00�� ��M�@�X�V�V���U��
�������������Ē����܂����B�\�肪�T�捪�Ƃ���܂����̂ŁAe��i���g���Ηǂ��Ȃ�
�z�������̂ł����A�F�X����Ă��邤���ɂT�{�p���g���Ă݂���ƑM���A�v�Z���Ă݂�� �Y��Ȓl�ɂȂ�̂ŋ��Q�v���܂����B�������A�����Ƃ������l�Ƃ͎��R�E�̕s�v�c���� �_�Ԍ������Ē����܂����B
��121���
��P.
��sin5��![]() ��sin�Ƃŕ\���ƁA
��sin�Ƃŕ\���ƁA
��sin5�Ɓ�sin(�R�Ɓ{�Q��)��sin�R��cos�Q�Ɓ{cos�R��sin�Q���ƂȂ�B
�����łR�{�p��Q�{�p�̌������g���ό`����ƁA
sin5�Ɓ�16sin5�Ɓ|20 sin3�Ɓ{5sin���ƂȂ�B
�����Asin5�Ɓ���(sin��)�ł���B
�����Ń��Ƀ�/�T�A�Q��/�T�A�R��/�T�A�S��/�T�A���������5�Ƃ͊e�X
�A�Q�A�R�A�S�ł���A���̒l�̓[���i�O�j�ł���B
�����Ă����S�̒l�͏�L�T��������̉��ł���A�v�X�̒l�͈قȂ�Asin(�^5)�Ȃ�
�S���[���i�O�j�łȂ��B
�����A��L��������sin�Ɓ��O�ȊO�̂S�̉��ł���B
������16sin4�Ɓ|20 sin2�Ɓ{5 ���O�ɉ��ƌW���̊W��K�p���A�T/1�U�����߂���̂ł���B
��Q.
��L�ƑS�����l�̌v�Z������Ƌ��߂���̂͂T/1�U�Ɠ����l�ɂȂ�B
�m�n�R�utoru�v����@�@�@ 6/17: 16��01�� ��M�@�X�V�V���U��
���P��=cos��/5+��sin��/5�Ƃ����ƃ�^5=-1 �����ŁAa=-(��+1/��),b=��^2+1/��^2
�Ƃ���ƃ�^4-��^3+��^2-��^1+1=0, ��� (��^2+1/��^2)-(��+1/��)+1=0����a+b=-1,
�܂�ab=-(��^2+1/��^2)(��+1/��)=-(��^3+1/��^3+��+1/��)=((��^2+1/��^2)-(��+1/
��))=a+b=-1����炩��Asin��/5 sin2��/5 sin3��/5
sin4��/5=(��-1/��) (��^2-1/
��^2)(��^3-1/��^3)(��^4-1/��^4))�^(2��)^4= (-2-(��+1/��))(-2-(��^3+1/��^3))
�^16=(-2-(��+1/��))(-2+(��^2+1/��^2))�^16=((-2+a)(-2+b))�^16=(4-2(a+b)+ab)
�^16=5/16--------�����@���łɃ������߂Ă݂�ƁAa,b�͕������@t^2+t-1=0�̂Q
��������a= -cos��/5<0�ƍ����čl���āAa=(-1-��5)�^2, b=(-1+��5)�^2�@���ꂩ��
���͎��������������ł��邱�Ƃ��l���āA��=(-a+��(4-a^2) ��)�^2=(��5+1)�^4 +
��(10-2��5)�^4 ���A�܂�sin��/5=��(10-2��5)�^4�A���l�Ƀ�^2=(b+��(4-b^2) ��)
�^2=(��5-1)�^4 +��(10+2��5)�^4 �� ��^3=-1/��^2=(-��5+1)�^4 +��(10+2��5)�^4
��,��^4=-1/��=-(��5+1)�^4 +��(10-2��5)�^4 �����̂S�̋������܂��߂ɂ�������
���Ă�5/16 �����Ƃ܂�܂��B
���Q cos��/10=sin(��/10+��/2)=sin3��/5, cos3��/10=sin(3��/10+��/2)=sin4
��/5, cos7��/10=sin(7��/10+��/2)=sin6��/5=-sin��/5, cos9��/10=sin(9��/10+
��/2)=sin7��/5=-sin2��/5, ����炩��cos��/10 cos3��/10 cos7��/10 cos9
��/10=sin��/5 sin2��/5 sin3��/5 sin4��/5=5/16�\�\�\�\����
�{����1/���Ȃǂ̂����Ƀ��̋��f�����i�o�[�j�Ƃ����������̂ł����L������
�܂������܂���ł����B��= cos2��/5+��sin2��/5 �Ƃ���P�̂T�捪�����߂邱��
�ɂȂ�܂����A���܂�v�Z���ȒP�ɂȂ�܂���ł����̂ŏ�L�̂܂܂ɂ��܂����B����
�ƃX�b�L�����������肻���ł����A���Ԃ����܂��ꂸ����͂���Œ��߂܂����B
���Q�͒P�ʉ~����ɐ��܊p�`�������ĂȂ��߂Ă���Ɩ��炩�Ȃ̂ł����A�}������
�Đ�������̂����܂��ł����A���낢��s���͎c��Ƃ���ł����A���̐l�����̉�@
���y���݂ɂ��Ă��܂��B
�m�n�S�u�O�p��K�v����@ 6/21: 22��23�� ��M �@�X�V�V���U��
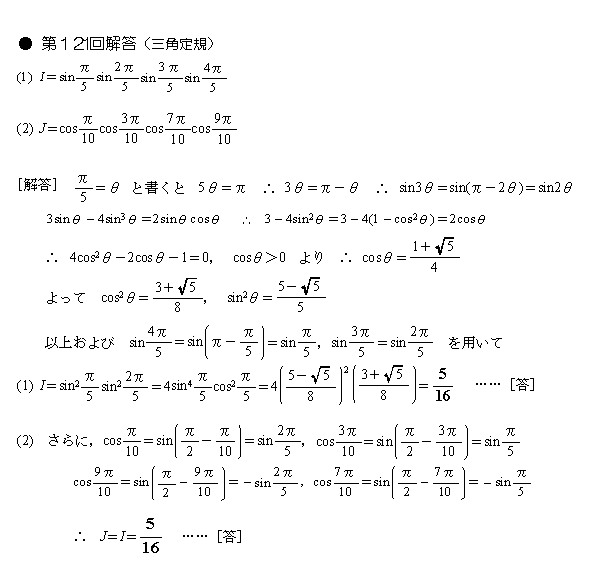
�m�n�T�u�j�[�X�P���X�v���� 6/23: 12��06����M �@�X�V�V���U��

�m�n�U�uUnderBird�v���� 6/24: 16��20���@��M �@�X�V�V���U��

�m�n�V�ukibomasa�v����@7/02: 21��28���@��M �@�X�V�V���U��
���P
��/5���R�U�x�Ȃ̂ŁA��p���V�Q�x�A���p�R�U�x�̓ӎO�p�`�ɂ����āA���p
�����ޕӂ̒������P�Ƃ��Ē�ӂ̒��������߂܂����B�]���藝�ɂ��cos�R�U�x
�̒l���킩��܂��B�Q�{�p�̒藝���cos72�x���킩��܂��B����āA���ꂼ��
��sin�̒l���킩��܂��B�����Ŕ��~�������A�T��������ƁA�usin��/5��sin4��
/5�Asin2��/5��sin3��/5�v�Ȃ̂ŗ\���́u�@{(sin��/5)^2}{sin3��/5)^2}�@�v��
�Ȃ�܂��B����āA�����́u5/16�v
��/5�@��cos�̒l�̕��q�́u1+��5�v�A2��/5�@��cos�̒l�̕��q�́u-1+��5�v�A��
�̂��ƂƁA�}�`�I�ɑΏ̂Ȃ��Ƃ���A3��/5�@��cos�̒l�̕��q�́u1-��5�v�A4��
/5�@��cos�̒l�̕��q�́u-1-��5�v�ł���B�i�����̂��Ƃ͔{�p���g���Ă���
�߂���B�j
���Q
���P�̗��p�����܂��B
�u��/5��2*��/10�v�A�u3��/5��2*3��/10�v�ł��邱�Ƃ��킩��B�����ł܂��A��
�~�������A10��������B�}�`�I�Ɍ��āA�ucos(��/10)��-cos(9��/10)�v�A
�ucos(3��/10)��-cos(7��/10)�v���A
�\���́@[ {cos(��/5)}^2 ]*[ {cos(3��/5)}^2
]�@�����Ƃ߂�悢�B�����ŁA
���ꂼ��̒l�͔{�p��苁�܂�܂��B����ē����́u5/16�v
�m�n�W�ukasama�v�@����@7/4�F22��17���@��M�@�@�X�V�V���U��
�����P�Fsin��/5�~sin2��/5�~sin3��/5�~sin4��/5
�@�}�I����
�@�ŋ߁A���q�̎Z�������Ă���Ă��邹���ŁA�}�I�ɉ��߂���Ȃ��t���Ă�����
���āE�E�E
�@y���ɑ��āAsin��/5�~sin2��/5��sin3��/5�~sin4��/5�͑Ώۂł��B����āA
sin��/5�~sin2��/5���v�Z���Ď��悷��Ηǂ��ƍl�����܂��B
�@���Z�����ɍl����ƁAsin(��-��)��sin���𗘗p����̂ł��傤���B
�Asin��/5�~sin3��/5�̎���̌v�Z
��L�̍l�@����Ɏ���ό`���܂��B
�@�^����{sin��/5�~sin2��/5}^2��{2�~(cos��/5-cos^3��/5)}
������ƃT�{���āAcos��/5=(��5+1)/4�͊��m�̂������ĉ������B������㎮��
����Đ�������ƁA��5/4�ƂȂ�܂��B
�����E�E�E�T/�P�U
�����Q�Fcos��/10�~cos3��/10�~cos7��/10�~cos9��/10
�����I�ɖ��P�̓����Ɠ����C�����܂����E�E�E����Ă݂�ƁA
�@�}�I����
�@����������l�ɁAcos��/10�~cos3��/10���v�Z���Ď��悷��Ηǂ��ƍl�����
�܂��B
�Acos��/10�~cos3��/10�̎���̌v�Z
�@���P�̌��ʂ�L���ɗ��p���܂��B
�@�@cos��/10��sin(��/2-��/10)��sin2��/5
�@�@cos3��/10��sin(��/2-3��/10)��sin��/5
�@�ƂȂ�܂�����A�v�Z����܂ł��Ȃ��A�����������܂��B
�����E�E�E�T/�P�U
�@
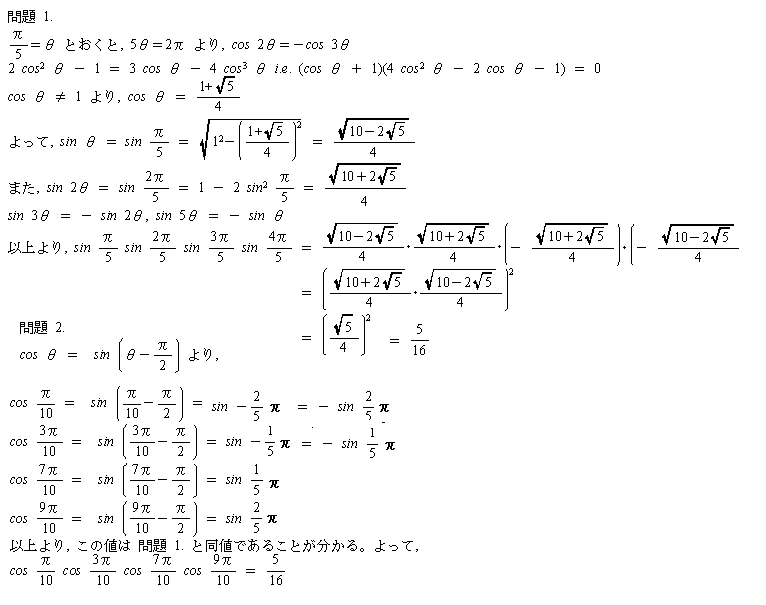 �@
�@�w��121��̉�����u�T�捪�E10�捪�v�̖�����ʉ��������̂������܂����B
(1)n��2�ȏ�̐����Ƃ���ƁA
�@�@��_{i=1}^{n-1}{sin(i��/n)} = n/{2^(n-1)}�@�ƂȂ�B
(2)n��3�ȏ�̊�Ƃ���ƁA
�@�@��_{i=1}^{(n-1)/2} {cos((2i-1)��/(2n))}
�@ ��_{i=(n+1)/2}^{n} {cos((2i-1)��/(2n))}= ((-1)^{(n-1)/2})n/{2^(n-1)}�@�ƂȂ�B
[�ؖ�]
(1)�Ă�1�̋�2n�捪 cos(��/n)+sqrt(-1)*sin(��/n)�Ƃ���B
��^(2n) = 1, ��^n = -1�@�͗e�Ղɓ�����B
��^i(i=1,2,...,2n-1)�݂͌��ɈقȂ�̂ŁA
x^(2n-1)+x^(2n-2)+...+x+1=(x-��)(x-��^2)(x-��^3)...(x-��^(2n-1))�@----- (*) �ƂȂ�B
(*)��x=1��������ƁA
�@2n=(1-��)(1-��^2)(1-��^3)...(1-��^(2n-1))
�܂�A��_{i=1}^{2n-1} {(1-��^i)} = 2n ��B
i=1,2,...,n-1�ɑ��āA
��^i = cos(i��/n)+sqrt(-1)*sin(i��/n)
��^(-i) = cos(i��/n)-sqrt(-1)*sin(i��/n) �Ȃ̂ŁA
sin(i��/n)=(��^i-��^(-i))/(2*sqrt(-1)) �ƂȂ�B
�@ ��^i-��^(-i)=-��^(-i)(1-��^(2i))=-��^(-i)(1-��^i)(1+��^i)
=-��^(-i)(1-��^i)(1-��^(n+i)) ���A
�@��_{i=1}^{n-1}{sin(i��/n)}
=(1/{(2*sqrt(-1))^(n-1)})��_{i=1}^{n-1}{��^i-��^(-i)}
= ({(-1)^(n-1)}/{(2*sqrt(-1))^(n-1)})*��_{i=1}^{n-1}{��^(-i)}
*(1/2)*��_{i=1}^{n-1}{1-��^i}*(1-��^n)*��_{i=1}^{n-1}{1-��^(n+i)}
=({(-1)^(n-1)}/{(2*sqrt(-1))^(n-1)})*��^{-n(n-1)/2}*(1/2)*��_{i=1}^{2n-1}{1-��^i}
= ({(-1)^(n-1)}/{(2*sqrt(-1))^(n-1)})*{sqrt(-1)^(n-1)}*(1/2)*(2n)
= n/{2^(n-1)} ��B
(2)n��3�ȏ�̊�Ȃ̂ŁAn=2m+1(m>=1)�Ƃ����B
i=1,2,...,m�ɑ��āA
�@cos((2i-1)��/(2n))=cos((2i-1+n)��/(2n)-��/2)=sin((2i-1+n)��/(2n))
=sin((i+m)��/n)
i=m+2,m+3,...,2m+1�ɑ��āA
�@cos((2i-1)��/(2n))=cos((2i-1-n)��/(2n)+��/2)=-sin((2i-1-n)��/(2n))
=-sin((i-1-m)��/n) �Ȃ̂ŁA(1)���A
�@��_{i=1}^{(n-1)/2} {cos((2i-1)��/(2n))} ��_{i=(n+1)/2}^{n}
{cos((2i-1)��/(2n))}= ��_{i=1}^{m} {sin((i+m)��/n)} ��_{i=m+2}^{2m+1} {-sin((i-1-m)��/n)}
= ��_{i=m+1}^{2m} {sin(i��/n)} *{(-1)^m}*��_{i=1}^{m} {sin(i��/n)}
= {(-1)^m}*��_{i=1}^{2m}{sin(i��/n)}
= {(-1)^((n-1)/2)}*��_{i=1}^{n-1}{sin(i��/n)}
= ((-1)^{(n-1)/2})*n/{2^(n-1)} ��B
[�NjL] �ȉ��������炭�ؖ��ł���Ǝv���܂��B
(3)n��2�ȏ�̋����Ƃ���ƁA
�@�@��_{i=1}^{n/2} {cos((2i-1)��/(2n))} ��_{i=(n/2)+1}^{n} {cos((2i-1)��/(2n))}
= {(-1)^(n/2)}/{2^(n-1)} �ƂȂ�B�x
<���̗���F�R�����g����ʉ��Ȃ�čl�������Ȃ���������ǂ��A�u�����v����̂������ł��B���肪�Ƃ��������܂��B
 �@
�@������@�@mizuryu@aqua.ocn.ne.jp
![]()
