暯惉侾俆擭俈寧俀俈擔
 [棳傟惎]
[棳傟惎]
丂丂丂丂丂丂丂丂戞侾俀俀夞悢妛揑側墳曞栤戣夝摎
丂丂丂丂丂丂丂丂丂丂亙夝摎曞廤婜娫丗俈寧俇擔乣俈寧俀俈擔亜
乵憹偊偨侾們倣俀乶
丂丂丂
懢榊偝傫偼丄寧梛擔戞俈尷偺乽憤崌揑側妛廗偺帪娫乿偵侾擭惗傪懳徾偵偟偰丄乽妝偟偄悢妛乿偲徧偟偨島嵗傪庴偗帩偭偰偄傑偡丅尰嵼偼乽僼傿儃僫僢僠悢楍乿偺挷傋妛廗傪偟偰偄傑偡丅偙偺拞偱丄師偺傛偆側壽戣傪惗搆偵揱偊偰偄傑偡丅
奆偝傫傕丄峫偊偰丄憹偊偨侾們倣俀丂偼偳偆偟偰偐丂峫偊偰偔偩偝偄丅
丂嶲峫丗乷倎値乸丗乷侾丆侾丆俀丆俁丆俆丆俉丆侾俁丆俀侾丆俁係丆俆俆丆俉俋丆丒丒丒乸傪僼傿儃僫僢僠悢楍偲偄偆丅
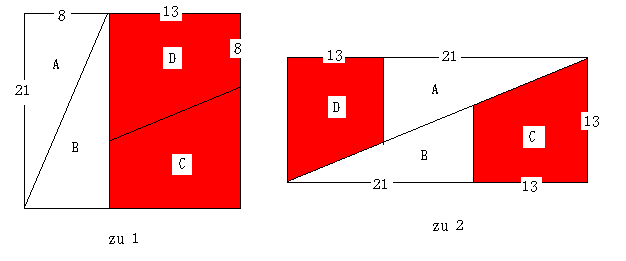
栤戣丗嵟弶丂侾曈偑俀侾們倣偺惓曽宍傪壓偺恾偺傛偆偵係偮偺晹暘偵暘偗傑偟偨丅嶰妏宍俙偲嶰妏宍俛偼崌摨丄
丂丂丂嶰妏宍俠偲嶰妏宍俢偼崌摨偱偡丅師偵丄偙偺係偮傪堏摦偝偣偰丄乵倸倳俀乶偺恾宍傪嶌傝傑偟偨丅
丂丂丂尒偨栚偼挿曽宍偱偡偐傜丄柺愊傪峫偊偰傒傞偲丄墶侾俁們倣丄廲乮侾俁亄俀侾乯們倣偵側傝傑偡丅
丂丂丂係偮偺晹暘傪堏摦偟偨偩偗偱偡偐傜丄柺愊偼摨偠偵側傞偼偢偱偡丅偳偆偟偰丄侾們倣俀堘偆偺偱偟傚偆偐丅
丂丂丂偙偺堘偄偼丄乽僼傿儃僫僢僠悢楍乿偵偳傫側惈幙偑偁傞偐傜偱偟傚偆偐丅
NO1乽kiyo乿偝傫丂丂丂7/06:
13帪32暘 庴怣
偄偮傕偍悽榖偵側偭偰偄傑偡丅kiyo偱偡丅
夝摎
F(n)=F(n-1)+F(n-2)丂
摿惈曽掱幃偼丄
X^2-X-1=0
俀崻傪兛丄兝 (兛>兝)
兛*兝=-1
丂丂丂F(n)=(兛^n-兝^n)/(兛-兝)
(1)
丂丂丂 F(n+1)*F(n-1)-F(n)^2=(-1)^n (2)
丂丂丂 (2)幃傪徹柧偡傞丅
嵍曈=((兛^(n+1)-兝^(n+1))/(兛-兝))*((兛^(n-1)-兝^(n-1))/(兛-兝))-((兛^n-兝^n)/(兛-兝))^2
丂丂 =(兛^(n-1)*兝^(n-1)*(2*兛*兝-兛^2-兝^2))/(兛-兝)^2
=((兛*兝)^(n-1))*(-1)
=(-1)^n =塃曈
丂丂丂乽悢妛偺晹壆乿偺乽崱廡偺栤戣乿偱徯夘偝傟偰偄傑偟偨丅
NO2乽Kashiwagi乿偝傫 7/06: 14帪49暘
庴怣
崱夞偺僼傿儃僫僢僠悢楍偼旕忢偵柺敀偄偱偡偹丅偙傫側偲偙傠偵傑偱僼傿儃僫僢僠悢楍偑娭學偟偰偄傞偲偼丒丒丒丒丅
屻敿偺娭學幃偼恾傪悢枃昤偄偰偄傞偆偪偵暘偐傝傑偟偨丅偟偐偟丄
徹柧偼柺搢側偺偱姩曎偟偰壓偝偄丅悢妛揑婣擺朄傪巊偆偺偱偟傚偆偹丅媂偟偔偛巜摫偺掱偍婅偄怽偟忋偘傑偡丅
戞122夞夝摎
丂zu2偺嶰妏宍B偺孹偒傪寁嶼偡傞偲8/21偱偁傞丅枖丄戜宍C偺孹偒偼(13-8)/13亖5/13偱偁傝丄5/13亜8/21偱偁傞丅傕偟丄zu2偺條側恾宍偑昤偗傞偲偡傞偲丄摉慠孹偒偼摍偟偔側偗傟偽側傜側偄丅偲偙傠偑摍偟偔側偄丄懄偪丄杮摉偼戜宍C偑嶰妏宍A偲廳側偭偰偍傝丄柺愊偼21亊21偱偁傞丅
僼傿儃僫僢僠悢楍偺抣傪怓乆曄偊偰zu1偲zu2傪嶌惉偟偰傒傞偲丄埲壓偺娭學偑惉棫偡傞帠偑暘偐傞丅栜榑丄悢妛揑婣擺朄偱徹柧偣偹偽偄偗側偄偺偱偟傚偆偑丄偦偙傑偱偼姩曎婅偄傑偡丅
値亞2偲偡傞偲丄
値偑嬼悢偺帪丂丂an2
= an+1 亊an-1亅 1
値偑婏悢偺帪丂丂an2
= an+1 亊an-1亄1
NO3乽kibomasa乿偝傫丂7/07:
03帪07暘 庴怣
乽栤戣122乿偺夝摎
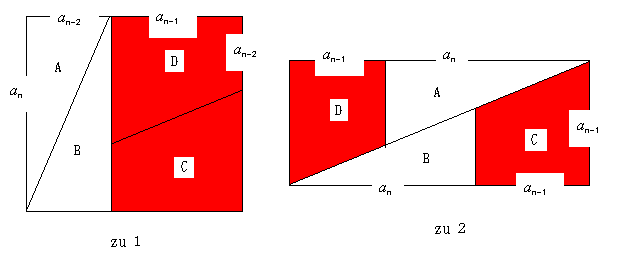
恾俀偵偍偄偰幚偼4揰ABCD偼堦捈慄偱偼偁傝傑偣傫丅埲壓偺傛偆側棟桼偵偍偗傞偐傜偱偡丅
恾侾偵偍偄偰丄巐妏宍D傪壓婰偺傛偆偵挿曽宍偲嶰妏宍偵暘妱偟傑偡丅嶰妏宍偺幬曈偺孹偒偼乽5/13乿偱偁傞丅偟偐偟丄恾B偵偍偄偰偼偳偆偐偲偄偆偲丄幬曈偺孹偒偼乽8/ 21乿偲側傞偙偲傛傝
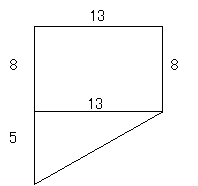

傛偭偰丄恾俀偵偍偗傞4揰ABCD偼捈慄偱偼側偔丄惓妋偵偼暯峴巐曈宍ABCD傪側偡丅偦偺柺愊偑侾傛傝丄偙偺傛偆側嶖妎傪堷偒婲偙偟偨丅
乽kibomasa乿偝傫 7/09: 23帪06暘 庴怣
僼傿儃僫僢僠悢楍偺掕媊傛傝峫偊傑偡丅
![]() 偨偩偟
偨偩偟![]() 偲偡傞丅
偲偡傞丅
偝偰丄偙偺堦斒崁傪媮傔傞丅
![]() 偺夝傪兛,兝偲偡傞丅
偺夝傪兛,兝偲偡傞丅
兛+兝亖1,兛兝亖亅1
摿惈曽掱幃傪梡偄傞偙偲傛傝
 乧嘆丂偲媮傔傜傟傞丅
乧嘆丂偲媮傔傜傟傞丅
偙偙偱兛亖![]() ,兝亖
,兝亖![]() 偲偍偔偙偲偵偡傞丅
偲偍偔偙偲偵偡傞丅
偝偰丄栤戣偺恾宍偵偍偄偰丄壓婰偺傛偆偵曈偺挿偝傪偍偔丅
偙偙偱丄偦傟偧傟偺柺愊傪媮傔丄柺愊偺嵎傪峫偊傞丅
(zu1)亖![]() 丆(zu2)亖
丆(zu2)亖![]() 丂傛傝
丂傛傝
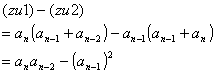 丂丂丂丂丂丂
丂丂丂丂丂丂
嘆傪戙擖偟偰丄
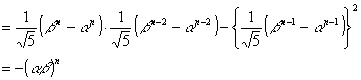
(丂堦斒偵偼丂![]() 偑惉傝棫偮傢偗偱偁傞丅)
偑惉傝棫偮傢偗偱偁傞丅)
偝偰丄偙偙偱偺栤戣偵娭偟偰丄n亖5丄兛兝亖亅1丂傛傝
(zu1)亅(zu2)亖亅(亅1)5亖1
偑惉傝棫偮丅
No4乽H7K乿偝傫 7/07: 19帪00暘 庴怣
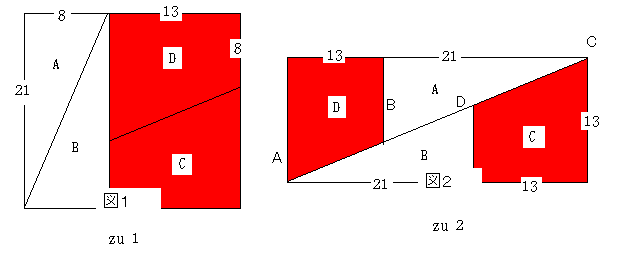
[zu1][zu2]偵偮偄偰偼丆
乽A丒B偺幬曈偺孹偒偲C丒D偺孹偒偑堘偆堊丆[zu2]偺乽懳妏慄乿偵尒偊傞偲偙傠偵偼幚偼寗娫偑偁傞偺偱側偔丄廳側偭偰偄傞偼偢偱偡丅
堦墳恾傪嶌偭偰傒傑偟偨丏
偙偺偙偲偑偱偒傞偺偼僼傿儃僫僢僠悢楍偺椬愙3崁傪fn,f(n+1),f(n+2)偲偟偨偲偒
fn*f(n+2)=(f(n+1))^2+(-1)^n
偲偄偆娭學偑偁傞偙偲偱暘偐傞丏
(f0=1,f1=1,f2=2,f3=3,...)
徹柧偼悢妛揑婣擺朄偵傛傞丏
乽H7K乿偝傫 7/07: 22帪22暘 庴怣
f(n+2)/fn=(f(n+1)+fn)/fn=f(n+1)/fn +1.
(f(n+1)/fn)^2=1+2 f(n-1)/fn+(f(n-1)/fn)^2.
傛傝
f(n+2)/fn-(f(n+1)/fn)^2=f(n+1)/fn-f(n-1)/fn-f(n-1)/fn-(f(n-1)/fn)^2
=f(n-2)/fn-(f(n-1)/fn)^2
therefore,
f(n+2)fn-(f(n+1))^2=f(n)f(n-2)-(f(n-1))^2.
g(n):=f(n+2)fn-(f(n+1))^2偲偡傞偲偙傟傛傝g(n)=g(n-2).
g(0)=1*2-1=1^2,g(1)=1*3-2^2=-1側偺偱
g(n)=(-1)^n.//
----
NO5乽kasama乿偝傫丂 7/08: 23帪24暘 庴怣
崱夞偼杮摉偵嫽枴怺偄栤戣偩偲巚偄傑偡丅堦
尒丄柺愊偑憹偊偰晄巚媍丠側婥偑偟傑偟偰丄偟偽傜偔峫偊崬傫偱偟傑偄傑偟偨丅
偨傇傫丄昞尰偼揔愗偱偼偁傝傑偣傫偑丄僼傿儃僫僢僠悢楍偺
丂A(n)丒A(n-2) - A(n-1) = 亇1 (n > 2)
偺惈幙傪墳梡偟偨栤戣偲悇懁偱偒傑偡丅揑奜傟偐傕偟傟傑偣傫偑丄偙偺悇應偑揔摉側傕偺偲偟偰丄挷傋偨寢壥傪婰嵹偟傑偡丅
堦晹暘丄崅峑悢妛偺斖埻傪挻偊傞抦幆傪巊偭偰偟傑偄傑偟偨乮曋棙側偺偱乯丅偟偐偟丄愄偺崅峑惗偼峴楍幃偵偮偄偰懡彮抦偭偰偄傑偟偨偟丄悈偺棳傟偝傫偺俫俹偵傾僋僙僗偟偰偔傞崅峑惗偼偒偭偲桪廏側恖偑懡偄偱偟傚偆偐傜栤戣側偄偲敾抐偝偣偰捀偒傑偟偨丅
巹偼愱栧壠偱偁傝傑偣傫偟丄傑偨曌嫮晄懌偱傕偁傞偨傔乮悢妛揑側嫽枴傪堦斒恖傛傝帩偭偰偄傞偩偗偱偡偺偱乯丄婰嵹偵偼懡乆晄旛偑偁傞偐偲巚偄傑偡丅偛巜揈捀偗傞偲桳傝擄偄偱偡丅
亙悈偺棳傟丗僐儊儞僩亜偄偄偊丄夝朄傊偺夁掱偼偄傠偄傠偲偁傝傑偡偐傜丄峔偄傑偣傫丅
嘆恾偺柺愊偺寁嶼
傑偢丄恾侾偺柺愊偼
丂柺愊侾 = A(n)亊{A(n-2) + A(n-1)} = A(n)^2 丒丒丒 (1)
偱偡偐傜丄戞値崁偺抣傪俀忔偟偨傕偺偱偡丅
傑偨丄恾俀偺柺愊偲巚傢傟傞傕偺偼
丂柺愊俀 = A(n-1)亊{A(n-1) + A(n)} = A(n-1)亊A(n+1) 丒丒丒 (2)
側偺偱丄戞値崁偺椉椬偺崁傪妡偗崌傢偣偨傕偺偱偡丅
嘇柺愊偺嵎偺寁嶼偲悇應
嘆偱媮傔偨柺愊偺嵎偼
丂嚈(n) = 柺愊俀 - 柺愊侾 = A(n-1)亊A(n+1) - A(n)^2 丒丒丒 (3)
偱偡丅嚈(n)偺抣傪弴偵寁嶼偡傞偲丄
丂嚈(2) = 1亊1 - 1^2 = 1
丂嚈(3) = 1亊3 - 2^2 = -1
丂嚈(4) = 2亊5 - 3^2 = 1
丂丂丂丂丒丒丒
偲側傝丄侾偲亅侾傪孞傝曉偡偺偱偼側偄偐偲悇應偱偒傑偡丅
嘊柺愊偺嵎偺娭學
偙偙偱丄崅峑悢妛偺斖埻傪彮偟偩偗挻偊偰媍榑偟傑偡乮偛傔傫側偝偄乯丅幃(3)
偼峴楍幃偺寁嶼幃偵傛偔帡偰偄傑偣傫偐丠丅幚嵺偺偲偙傠丄埲壓偺峴楍幃偦偺傕
偺偱偡丅
丂|A(n-1) A(n) |
嚈(n) = |
|
丂|A(n) A(n+1)|
忋婰偺峴楍幃偵拝栚偟偰丄嚈(n)偲嚈(n+1)偺娭學傪挷傋傑偡丅
峴楍幃偺侾楍栚偵俀楍栚傪壛偊傑偡乮峴楍幃偺惈幙偱偡偑丄偁傞楍偵暿偺楍偵偨
偟偰傕抣偼曄傢傝傑偣傫乯丅
丂|A(n-1) A(n) | |A(n-1)+A(n) A(n)
| |A(n+1) A(n) |
丂| | =
|
| = | |
丂|A(n) A(n+1)| |A(n)+A(n+1)
A(n+1)| |A(n+2) A(n+1)|
侾楍栚偲俀楍栚傪擖傟懼偊傑偡乮偙偺応崌峴楍幃偺晞崋偑斀揮偟傑偡乯丅
丂|A(n+1) A(n) | |A(n)
A(n+1)|
丂| | =
-1亊| |
= -嚈(n+1)
丂|A(n+2) A(n+1)| |A(n+1) A(n+2)|
傛偭偰丄柺愊嵎偼侾偲亅侾傪孞傝曉偟傑偡丅
嘋寢榑
丂値亜俀偺応崌丄戞値崁偺俀忔偲偦偺椉懁乮戞値亅侾崁丄戞値亄侾崁乯偲偺嵎偼
侾傑偨偼亅侾偱偡丅
亙悈偺棳傟丗僐儊儞僩亜偱丄傕偆侾偮旈枾偑偁傞傫偱偡傛丅偳偆偟偰丄恾俀偑嶌傟傞偐側傫偱偡丅
偙偺揰傪峫偊偰偔偩偝偄丅 僸儞僩偼俀崁偺斾偵偁傝傑偡丅
乽kasama乿偝傫 7/10: 20帪52暘 庴怣
丂偦偆偱偡偹丅偛巜揈偺傛偆偵恾俀傪嶌傟傞棟桼傑偱偼峫偊偰偄傑偣傫偱偟偨丅
丂僼傿儃僫僢僠悢楍偲墿嬥斾偲偺娭學偼嵟傕椙偔抦傜傟偰偄傑偡偑丄恾俀偑嶌惉
偱偒傞偙偲偲壗偐娭學偁傞傛偆側婥偑偟傑偡丅偙偺曈傝傪挷嵏偟偰傒傑偡丅
丂摎偊偑傢偐傝傑偟偨傜丄嵞搙曉摎偝偣偰捀偒傑偡丅偦偺偲偒偼傛傠偟偔偍婅偄
抳偟傑偡丅
乽kasama乿偝傫 7/11: 23帪43暘 庴怣
偛巜揈捀偄偨俀崁偺斾偵偮偄偰峫偊偰傒傑偟偨丅
僼傿儃僫僢僠悢楍偺惈幙偺拞偱乽俀崁偺斾乿偼嵟傕戝愗側偙偲偱偡偹丅尒棊偲偟偰偄傑偟偨丅
偄傠傫側暥專傗嶨帍偵僼傿儃僫僢僠悢楍偵偮偄偰彂偐傟偰偄傞偺傪椙偔栚偵偟傑偡丅
悈偺棳傟偝傫偺俫俹偱傕僼傿儃僫僢僠悢楍偺堦斒崁偲曣娭悢偵偮偄偰偺婰嵹偑偁傝傑偟偨乮愭擔僇僞儔儞悢傪挷傋偰偄偨偲偒偵婥晅偒傑偟偨乯丅偟偐偟丄戝恖偵側偭偰丄崱夞偺傛偆偵僼傿儃僫僢僠悢楍偵偮偄偰偁傟偙傟偲挷傋偰傒傞婡夛偼偁傝傑偣傫偱偟偨乮巇帠偱巊偆悢妛側傫偰掱搙偑掅偄偟斖埻偑尷傜傟偰偄傑偡偐傜偹丒丒丒乯丅
挷嵏偺夁掱偱丄崱傑偱抦傜側偐偭偨偙偲偵傕婥晅偒傑偟偨丅乽偁乣僼傿儃僫僢僠悢楍偵偦傫側惈幙偑偁傞偩乿側偳姶寖偟偨偙偲偑懡乆偁傝傑偟偨丅椙偔抦傜傟偰偼偄偰傕丄側偐側偐墱偺怺偄傕偺偱偡偹丅
丂埲壓偵丄峫偊偨偙偲傪婰嵹偝偣偰捀偒傑偡偑丄晄旛側偳懡乆偁傞偐偲巚偄傑偡丅偛巜揈捀偗傞偲桳傝擄偄偱偡丅
恾俀偺挿曽宍偺傛偆側恾宍傪嶌傞偵偼丄嶰妏宍A丄B偲戜宍C丄D傪挿曈乮嵟傕挿偄曈乯偱挘傝崌傢偣傞昁梫偑偁傝傑偡丅
恾偑側偄偲愢柧偟擄偄偺偱偡偑丄棎朶側尵偄曽偱偡偑丄帇妎揑偵嶰妏宍偺挿曈偲戜宍偺挿曈偺孹偒偑傎傏摨偠偱偁傟偽丄
挿曽宍偺傛偆側恾宍偼嶌惉偱偒傞偲峫偊傑偟偨丅
---- 埲壓偼夞摎偱偡 ----------------------------------------------------
恾宍傪堏摦偝偣偰丄恾俀偺傛偆側宍傪嶌傞偲丄彮偟寗娫偑偱偒偰偟傑偄傑偡偹丅
壗屘側傜丄嶰妏宍偲戜宍偺嵟傕挿偄曈乮埲壓丄挿曈偲屇傇乯傪宷偓崌傢偣偨偲偒偵丄孹偒偑彮偟堘偆偺偱丄僺僢僞儕偲偼挘傝崌傢偣傞偙偲偑偱偒側偄偐傜偱偡丅偱傕丄捈姶揑偵悢偑戝偒偔側傞偲丄寗娫偼偩傫偩傫彫偝偔側偭偰偔傞傛偆側婥偑偟傑偣傫偐丠
寗娫偺嬶崌偼孹偒偵娭學偟偰偄傞栿偱丄奺曈偺挿偝偑戝偒偔側傞偵偟偨偑偄丄嶰妏宍偲戜宍偺挿曈偺孹偒偑偁傞堦掕抣偵嬤偯偔偺偱偼丠偲偄偆偙偲偵拝栚偟偰傒傑偟偨丅
嘆嶰妏宍偲戜宍偺挿曈偺孹偒
A(n)丄A(n-1)丄A(n-2)偺俁偮偺崁傪巊偭偰丄恾俀傪慻傒棫偰偲偒
嶰妏宍偺挿曈偺孹偒偼
丂A(n-2)/A(n) = 1 - A(n-1)/A(n) 丒丒丒(1)
堦曽丄戜宍偺挿曈偺孹偒偼
丂{A(n-1)-A(n-2)}/A(n-1) = 1 - A(n-2)/A(n-1)丒丒丒(2)
偲側傑偡丅偮傑傝丄孹偒偼悢楍偺椬傝崌偆俀崁偺斾偵娭學偟偰偄傑偡丅
嘇悢楍偺椬傝崌偆俀崁偺斾
傑偢丄A(n) = A(n-1) + A(n-2)偺椉曈傪A(n-1)偱妱傞偲丄
丂A(n)/A(n-1) = 1 + A(n-2)/A(n-1)
偲側傝傑偡丅彮偟棎朶偱偡偑乮偁傞掱搙寢壥偑傢偐偭偰偄傞偺偱乯丄A(n)/A(n-1)
偑n仺亣偺偲偒偵兛偵廂懇偡傞傕偺偲峫傟偽丄
丂兛 = 1 + 1/兛
偱偡丅兛 = (併5亇1)/2偲側傝傑偡偑丄兛=(併5-1)/2<1偼晄搒崌側偺偱丄兛=(併
5+1)/2偱偡丅偮傑傝丄A(n)/A(n-1)偼n仺亣偺偲偒偵(併5+1)/2偵廂懇偡傞偲峫偊傜傟傑偡丅
偙偺斾偼偄傢偄傞墿嬥悢偩偦偆偱丄廲墶偺斾偑墿嬥斾偵嬤偄挿曽宍偑嵟傕旤偟偄偲偝傟偰偄傑偡丅
嘊挿曈偺孹偒偲墿嬥斾
嘆丄嘇偺峫嶡傛傝丄崁偑戝偒偔側傞偵偟偨偑偄丄幃(1)丄(2)偼摨偠抣偵嬤偯偒傑偡丅偮傑傝丄恾俀偺挿曽宍偺傛偆側恾宍偑尷傝側偔挿曽宍偵嬤偯偒傑偡丅偙傟偑丄恾俀傪嶌惉偱偒傞棟桼偲峫偊傜傟傑偡丅
NO6乽toru乿偝傫丂丂丂7/15: 11帪34暘 庴怣
戞侾俀俀夞栤戣偵墳曞偄偨偟傑偡丅乽憤崌妛廗乿妝偟偦偆偱偡偹丅崅峑堦擭惗偲偄偊偽丄侾俆嵥偐侾俇嵥偱偡丄
偦偺偙傠偙傫側愭惗偑偄傟偽,傕偭偲悢妛偑岲偒偵側偭偰偄偨偩傠偆側偲巚偄傑偡丅丂
枅夞,弌戣傪妝偟傒偵偟偰偄傑偡丅栤戣嶌惉偨偄傊傫偱偟傚偆偑丄偙傟偐傜傕丄傛傠偟偔偍婅偄偟傑偡丅丂儁儞僱乕儉丂俿倧倰倳
夝摎丂A偲D傪ZU俀偺傛偆偵暲傋偨応崌丄巐妏宍D偺堦斣彫偝偄妏兛丄嶰妏宍A偺捈妏埲
奜偱戝偒偄曽偺妏傪兝偲偡傞偲tan兛=13/5<21/8=tan兝
傛傝兛亙兝偱幬曈偼ZU俀偺傛
偆偵堦捈慄偵偼側傜偢偵丄愜傟慄偵側傞丅B丄C偵娭偟偰傕摨條偱丄傑傫拞偵偡偒娫偑
偱偒傞丅偙偺柺愊偑侾cm2偲偄偆偙偲偱偡偹丅
僼傿儃僫僢僠偺悢楍偺戞n崁傪a(n)偲偡傞偲a(n+2)=a(n+1)+a(n)丄a(1)=a(2)=1,
a(n)^2+a(n+1)^2=a(n)(a(n)+a(n+1))+a(n+1)(a(n+1)-a(n))=a(n)a(n+2)+a(n+1)a(n-1
) (n亞2)
乮堦曈偑a(n)偲a(n+1)偺惓曽宍傪墶偵暲傋偰丄挿曽宍擇偮偵嬫愗傝側偍偟偨乯傛傝
a(n+1)^2-a(n)a(n+2)=-(a(n)^2-a(n+1)a(n-1))=(-1)^(n-1)(a(2)^2-a(1)a(3))=(-1)^
n (n=1偱傕惉棫)偲側傞偐傜丄僼傿儃僫僢僠偺悢楍偺楢懕偡傞俁崁傪偲傞帪丄傑傫拞
偺崁偺暯曽偲戞侾崁偲戞俁崁偺愊偺嵎偺愨懳抣偼忢偵侾偵側偭偰偄傞丅
乽toru乿偝傫 7/17: 12帪20暘 庴怣
屼巜揈偺丄僼傿儃僫僢僠偺悢楍偺俀崁娫偺斾偵偮偄偰彮偟峫偊偰傒傑偟偨偺偱丄嵞搙
墳曞偝偣偰捀偒傑偡丅側偐側偐旤偟偄寢壥偱丄妝偟傑偣偰捀偒傑偟偨丅偁傝偑偲偆偛
偞偄傑偡丅丂儁儞僱乕儉丂俿倧倰倳
慜夞媮傔偨俁崁娫偺幃a(n+1)^2-a(n)a(n+2)= (-1)^n丂偺椉曈傪-a(n)a(n+1)偱妱偭偰丄
a(n+2)乛a(n+1) -a(n+1)乛a(n) = (-1)^(n-1)乛a(n)a(n+1),丂
b(n)= a(n+1)乛a(n), c(n)=1乛a(n)a(n+1)偲偡傞偲b(n+1)-b(n)= (-1)^(n-1) c(n),
b(1)=1丄c(n)>0,偱 b(n)-1=c(1)-c(2)+c(3)-c(4)+------c(n-1) (n亞2)偲偄偆岎戙媺
悢偺宍偵側偭偰偄傞丅c(n)>c(n+1)傛傝丄
2=b(2)>b(4)> --- >b(2m)> --- >b(2m+1)> ---
>b(3)>b(1)=1偑惉傝棫偪丄 n仺亣偺
帪b(2m)-b(2m+1)=c(2m)仺侽傛傝b(n)偼廂懇偡傞偙偲偑暘偐傞丅a(n+2)=a(n+1)+a(n)
傪a(n+1)偱妱偭偰b(n+1)=1+1/b(n)偺椉曈偱n仺亣偲偡傟偽丄b(n)偑廂懇偡傞偙偲偼暘
偐偭偰偄傞偺偱偙傟傪b偲偡傞偲b=1+1/b丂(1<b<2)傪夝偄偰b=(1+併5)乛2丂偮傑傝丄
僼傿儃僫僢僠悢楍偺俀崁娫偺斾偺悢楍b(n)偼侾偲俀偺娫傪偩傫偩傫怳暆傪彫偝偔偟側
偑傜怳摦偟堦揰b=(1+併5)乛2丂傊嬤偯偄偰偄偔偙偲偑暘偐傞丅堦捈慄偵尒偊傞偙偲傪
尵偆偨傔偵偼偝傜偵廂懇偺僗僺乕僪偑懍偄偙偲傪尵偆昁梫偑偁傝偦偆偱偡偑丄
乥b(n)-b乥<c(n)=1乛a(n)a(n+1)偩偐傜懍偦偆偱偡偑丄偳傫側傕偺偱偟傚偆丠
丂丂丂丂亙帺戭亜丂丂mizuryu@aqua.ocn.ne.jp
![]()
