�����P�T�N�W���P�V��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@�@�@�@��P�Q�R�����w�I�ȉ������NO�Q
�@�@�@�@�@�@�@�@�@�@����W���ԁF�V���Q�V���`�W���P�V����
�m�t�B�{�i�b�`�����n
�@�@�@
���Y����́A���j����V���́u�����I�Ȋw�K�̎��ԁv�ɂP�N����Ώۂɂ��āA�u�y�������w�v�Ə̂����u���������Ă��܂��B���݂́u�t�B�{�i�b�`����v�̒��w�K�����Ă��܂��B���̒��ŁA���̂悤�Ȑ���������̂ł͂Ȃ����Ɛ��k�ɓ`���Ă��܂��B
�@�Q�l�F�o�����p�F�o�P�C�P�C�Q�C�R�C�T�C�W�C�P�R�C�Q�P�C�R�S�C�T�T�C�W�X�C�E�E�E�p���t�B�{�i�b�`����Ƃ����B

H
(Hn�|�d)
��
H
�{H2�{�E�E�E�{Hn-1
�g
��
��
-
1
�|
�P
�P
�P
�O
�O
�P
�P
�P
��
(
H�|�d)-1
H
2
��
�P
�P
�P
�Q
��
�{
�P
�O
�O
�P
�O
�P
�P
�P
��
H
�{�d
H
n+1
��
��
�e
n
�e
n+1
�e
n+1
�e
n+2
��
�e
n
F
n+1
F
n+Fn-1
F
n+Fn+1
�O
�P
�P
�P
��
�e
n-1
�e
n
�e
n
�e
n+1
H
n�E�g
��
�O
�P
�P
�P
�e
0
�e
1
�e
1
�e
2
��
H
��
H
n
�e
n-1
�e
n
�e
n

�F����A�l�������킩������A�S���łȂ��Ă����ł�����A�ƃy���l�[����Y���āA���[���ő����Ă��������B
�҂��Ă��܂��B
�m�n�P�uH7K�v���� 7/26:
10��34�� ��M �X�V8/17
�A�[�@�łȂ��Ă�������悤�ȋC�������ł���...
1: ��n=1,2�̂Ƃ�
�@�@1+F1=2=F3.����
1+F1+F2=3=F4.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�C1+F1+F2+...+Fk=F(k+2)�Ɖ��肷���
�@�@ ���ӂ�F(k+1)�𑫂��C1+F1+F2+...+Fk+F(k+1)=F(k+2)+F(k+1)=F(k+3)=F(k+1+2).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
2: ��n=1,2�̂Ƃ�
�@�@ F1=F2.����
�@�@ F1+F3=3=F4.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�CF1+F3+...+F(2k-1)=F(2k)�Ɖ��肷���
�@�@ ���ӂ�F(2k+1)�𑫂��CF1+F3+...+F(2k-1)+F(2k+1)=F(2k)+F(2k+1)=F(2k+2)
����F1+F3+...+F(2k-1)+F(2(k+1)-1)=F(2(k+1)).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
3: ��n=1,2�̂Ƃ�
�@�@1+F2=2=F3.����
1+F2+F4=5=F6.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�C1+F2+F4+...+F(2k)=F(2k+1)�Ɖ��肷���
�@�@ ���ӂ�F(2k+2)�𑫂��C1+F2+F4+...+F(2k)+F(2k+2)=F(2k+1)+F(2k+2)=F(2k+3)
����1+F2+F4+...+F(2k)+F(2(k+1))=F(2(k+1)+1)
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
4: �u�Δ�сv�ōl����D
�@�@O O O O ...O O O��2n+1���̐�����C������1,2,3,..,2n+1�̔ԍ����t���Ă���Ƃ���D
�@�@�����ŁC1��n�܂Ŕ�ԁi�A�������̂�1������̂݁j�Ƃ���ƁC���̏ꍇ�̒ʂ萔��F(n).
�@�@����C2n+1��ԏꍇ��
�@�@�En-1��n+1���ԁin�͒ʉ߁jF(n-1)F(2)F(n+1)=F(n-1)F(n+1)�ʂ�
�@�@�En���ԁc�cFnF(n+2)=Fn^2+Fn(Fn+1)�ʂ�
�@�@�Ȃ̂ŁC�vFn^2+(F(n-1)+Fn)F(n+1)=Fn^2+F(n-1)^2�ʂ肾���C�S�̂͂܂�F(2n+1)�ʂ�ł�����͂��C
�@�@����Ď����ꂽ�D
5: ��n=1,2�̂Ƃ�
�@ F1^2=1=F1F2.����
F1^2+F2^2=2=F2F3.����
��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@ �@���Ȃ킿�CF1^2+F2^2+...+Fk^2=FkF(k+1)�Ɖ��肷���
�@ �@���ӂ�F(k+1)^2�������CF1^2+F2^2+...+Fk^2+F(k+1)^2=FkF(k+1)+F(k+1)^2=F(k+2)F(k+1)=F(k+1)F(k+1+1).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
�m�n�Q�utoru�v����@�@�@7/29: 13��54�� ��M �X�V8/17
�P�DFn+2�\Fn+1��Fn �@�ɂ�����n=1,2,3,------,n�Ƃ��ĕӕӂ�������Fn+2�\F2��F1
�{F2�{F3�{-------�{Fn F2��1�����琫���P�����藧�B
�Q�DF2n+2�\F2n��F2n+1 (n=1,2,3----)��, F0��0�Ƃ����n=0�ł����藧����A
n=0,1,2,3,------,n-1 �Ƃ��ĕӕӂ�����F2n��F1�{F3�{F5�{---�{F2n-1
�R�D F2n+1�\F2n-1��F2n �ɂ�����n=1,2,3,------,n�Ƃ��ĕӕӂ�������F2n+1�\F1
��F2�{F4�{F6�{-------�{F2n, F1��1�����琫��3�����藧�B
�S�D F2n��2FnFn+1�\Fn^2, F2n+1��Fn^2�{Fn+1^2�Ɖ��肵�Đ��w�I�A�[�@�ŏؖ�����A
n=1�̂Ƃ�F2=2F1F2�\F1^2��1,F3=F1^2�{F2^2��2,�Ő��藧�An=n+1�Ƃ��āAF2n+2
��F2n�{F2n+1��(2FnFn+1�\Fn^2)�{(Fn^2�{Fn+1^2)��2FnFn+1�{Fn+1^2��2(Fn+2
�\Fn+1)Fn+1�{Fn+1^2��2Fn+1Fn+2�\Fn+1^2, F2n+3��F2n+1�{F2n+2��(Fn^2�{Fn+1^2)
�{(2Fn+1Fn+2�\Fn+1^2)��Fn^2�{2Fn+1Fn+2��(Fn+2�\Fn+1)^2�{2Fn+1Fn+2��Fn+1^2
�{Fn+2^2 ��萫���S�͏ؖ����ꂽ�B
�T�DFn+1Fn+2�\FnFn+1��Fn+1(Fn+Fn+1)�\FnFn+1=Fn+1^2 �ɂ�����F0=0 �Ƃ������
��n=0�ł����藧����n=0,1,2,---n-1�Ƃ��ĕӕӂ����AFnFn+1��F1^2�{F2^2
�{F3^2�{-------�{Fn^2
���R�����g�������P�A�Q�A�R�A�T�����w�I�A�[�@���g���ΊȒP�ɏؖ��ł��܂����A�ǂ�������^�����Ċm���߂Ă��邾���̂悤�ŋC�ɓ���Ȃ��̂ŁA�Ȃ�ł���Ȏ����o�Ă���̂��l�����ł��A���ړ����Ă݂܂����B�Ƃ��낪�A�ǂ����S�͂��܂��s�����Ɍ��NjA�[�@���g������ɂ��܂�X�}�[�g�łȂ��ɂȂ��Ă��܂��܂����B�����ƁA�����ƃG
���K���g�ȕ��@������̂ł��傤���A�Ȃ��Ȃ����Ԃ��Ƃꂸ�A��肠�������𑗂��Ă����܂��B�@
�utoru�v���� 8/01: 11��07��
��M �X�V8/17
�t�B�{�i�b�`����F0=0,F1=1,Fn+2=Fn+1+Fn (n=0,1,2---)�̈�ʍ���x^2-x-1=0�̂Q��
�����A��(��<��)�Ƃ���� ���{��=1,����=-1�� Fn=(��^n�\��^n)�^(���\��)�@
������(��^(2n+1)�\��^(2n+1))(���\��)����^2(n+1)�{��^2(n+1)�{��^(2n)�{��^(2n)
��(��^n�{��^n)^2�{(��^(n+1)�{��^(n+1))^2�����藧����A���ӂ�(���\��)^2�Ŋ�
��AF2n+1��Fn^2�{Fn+1^2�����藧���Ƃ�������܂��B�����Ń���=-1�͎g���Ă�
�܂����A���{��=1�̕��͎g���Ă��܂���̂ŁA���̊W��F0=0,F1=1,Fn+2=kFn+1+Fn
�ł����藧�Ǝv���܂��B�Ⴆ��k���Q�Ƃ���ƁA���̐���
��(0),1,2,5,12,29,70,169,408,985,2378,5741,-----�ƂȂ�܂����A1^2+2^2=5,
2^2+5^2=29, 5^2+12^2=169 �Ƃ����悤�Ȋ����Ő��藧���Ă��܂��B
���R�����g�������S�ɂ��ĕʉ�������Ă݂܂����B��ʉ������߂Ă��育��v�Z����̂͂ǂ����Ƃ��v���܂������A����Ă݂�Ƃ��̖��Ɋւ��Ă͂��̕����悢���ƁH�A�ǂ�Ȃ���ł��傤�B
�m�n�R�ukasama�v����@ 7/29: 23��01�� ��M �X�V8/17
�y�����P�z
�@�Q������K���ɑ��삷��Əo�������ł��ˁB�Q���������Ԃɕ��ׂĂ݂�ƁA
�@�@F(n) + F(n+1) = F(n+2)
�@�@F(n-1) + F(n) = F(n+1)
�@�@F(n-2) + F(n-1) = F(n)
�@�@�@�@�@�E�E�E
�@�@F(1) + F(2) = F(3)�@�ƂȂ�܂��B�����̎������Z�����
�@2�~{F(1)+F(2)+�E�E�E+F(n)} - F(1) + F(n+1) =
�@�@ {F(1)+F(2)+�E�E�E+F(n)} - F(1) - F(2) + F(n+1) + F(n+2)
�@�� F(1)+F(2)+�E�E�E+F(n) = F(n+2) - F(2)
�@�ƂȂ�܂��B�����ŁAF(2)=1�ł����琫���P�͐��藧���܂��B�ȉ��̐����Q�A�R���瓱�����Ƃ��ł���Ǝv���܂��B�ł����Ԓʂ�ɁI
�y�����Q�z
�@������Q������K���ɑ��삷��Əo�������ł��ˁB
�@�@F(2n) = F(2n-1) + F(2n-2)
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-4)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-5) + �E�E�E + F(3) + F(2)
�@�����ŁAF(2)=F(1)�ł�����A�����Q�͐��藧���܂��B
�y�����R�z
�@��������l�ɂ���
�@�@F(2n+1) = F(2n) + F(2n-1)
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-3)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-4) + �E�E�E + F(2) + F(1)
�@�����ŁAF(1)=1�ł�����A�����R�͐��藧���܂��B
�y�����S�z
�@���[�����A�Q���������܂��ό`����Ƃł���(�H)��������܂��A�Z�ʂ��Ȃ��̂ŏ�����蓹�����čl���܂����B
�@�܂��A�����ʂ̕�������l���āA���R��m�An�ɑ��āA
F(n) = F(m+1)F(n-m) + F(m)F(n-m-1) �E�E�E (1)
�@�����藧���Ƃ��m���߂܂��Bm�Ɋւ��鐔�w�I�A�[�@�ŏؖ����܂��B
�@m=1�̏ꍇ
�@F(n) = F(1+1)F(n-1) + F(1)F(n-1-1)
�@�@�@ = F(2)F(n-1) + F(1)F(n-2)
�@�@�@ = F(n-1) + F(n-2)
�@�ƂȂ萬�藧���܂��B
�Am=k�̂Ƃ�(1)������������Ƃ��āAm=k+1�̏ꍇ
�@������A
�@�@F(n) = F(k+1)F(n-k) + F(k)F(n-k-1)
�@�ł��B�����ό`���āA
�@�@F(n) = F(k+1){F(n-k-1) + F(n-k-2)} + F(k)F(n-k-1)
�@�@�@�@ = F(k+1)F(n-k-1) + F(k+1)F(n-k-2) + F(k)F(n-k-1)
�@�@�@�@ = {F(k+1) + F(k)}F(n-k-1) + F(k+1)F(n-k-2)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����A(1)����m=k+1��������
�@�@F(n) = F((k+1)+1)F(n-(k+1)) + F(k+1)F(n-(k+1)-1)
�@�@�@�@ = F(k+1+1)F(n-k-1) + F(k+1)F(n-k-1-1)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����āAm=k+1�̏ꍇ�����藧���܂��B
�B��L�@�A�A��肷�ׂĂ̎��R��m�An�ɑ��āA(1)�������藧���܂��B
�@���āA���Ȃ蓹�������Ă��܂��܂������A���������ł��B(1)�ɂ�����n��2n+1�Am��n�Ƃ����
�@�@F(2n+1) = F(n+1)F(2n+1-n) + F(n)F(2n+1-n-1)
�@�@�@�@�@�@= F(n+1)^2 + F(n)^2
�@����āA�����S�͐��藧���܂��B
�y�����T�z
�@�����������蓹�����܂��B
�@�@F(i)F(i+1) = F(i){F(i-1)
+ F(i)} = F(i)F(i-1) +
F(i)^2
�@�@�� F(i)^2 = F(i)F(i+1)
- F(i)F(i-1) �E�E�E(1)
�@(1)����i=2,3,�E�E�E,n�͈̔͂ʼn��Z�����
�@�@���� = F(2)^2 + F(3)^2 + �E�E�E + F(n)^2
�@�@�E�� = F(2)F(3) + F(3)F(4) + �E�E�E + F(n)F(n+1)
�@�@�@�@ - { F(2)F(1) + F(3)F(2) + �E�E�E + F(n)F(n-1) }
�@�@�@�@ = F(n)F(n+1) - F(2)F(1)
�@�܂�A
�@�@F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1) - F(2)F(1)
�@�ƂȂ�AF(2)=F(1)=F(1)^2�ɒ��ӂ���ƁA
�@�@F(1)^2 + F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1)
�@����āA�����T�͐��藧���܂��B
���R�����g�����āA���肸�ɑ�123����ɒ��킵�Ă݂܂����i��Ƃ𑝂₵�Ă��܂����Ƃ������ى������j�B
�@���̃t�B�{�i�b�`����̊W���͂悭�ڂɂ��܂����A�u�ؖ����Ă݂ĉ������v�ƌ�����ƁE�E�E���[��ƌ����������ł��ˁB�ł����Ƃ������t����]�����ďؖ��������肷�B��{�I�ɂ́A�R�c�R�c�Ɛ��w�I�A�[�@�ł��A���ׂďؖ��ł�����̂Ǝv���܂����A�����S�ȊO�͑Q������ό`���ďؖ����Ă݂܂����B
�ukasama�v���� 8/01: 22��41�� ��M �X�V817
�y�����z
�@�O��̖��ł͍s�i����͑�w�ŏK���j���g���Ă��܂��܂������A����͍��Z���w�ŏK���s��𗘗p���܂��B�����Ȃ�ؖ�����̂͑�ςȂ̂ŏ��������̑������Ă����܂��B
�܂��A�t�B�{�i�b�`������ȉ��̂悤�ȍs��ŕ\�����܂��B
|
|
NO3�uKasama�v���� 7/29: 23��01�� ��M �X�V8/17
�y�����P�z
�@�Q������K���ɑ��삷��Əo�������ł��ˁB�Q���������Ԃɕ��ׂĂ݂�ƁA
�@�@F(n) + F(n+1) = F(n+2)
�@�@F(n-1) + F(n) = F(n+1)
�@�@F(n-2) + F(n-1) = F(n)
�@�@�@�@�@�E�E�E
�@�@F(1) + F(2) = F(3)
�@�ƂȂ�܂��B�����̎������Z�����
�@2�~{F(1)+F(2)+�E�E�E+F(n)} - F(1) + F(n+1) =
�@�@ {F(1)+F(2)+�E�E�E+F(n)} - F(1) - F(2) + F(n+1) + F(n+2)
�@�� F(1)+F(2)+�E�E�E+F(n) = F(n+2) - F(2)
�@�ƂȂ�܂��B�����ŁAF(2)=1�ł����琫���P�͐��藧���܂��B�ȉ��̐����Q�A
�R���瓱�����Ƃ��ł���Ǝv���܂��B�ł����Ԓʂ�ɁI
�y�����Q�z
�@������Q������K���ɑ��삷��Əo�������ł��ˁB
�@�@F(2n) = F(2n-1) + F(2n-2)
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-4)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-5) + �E�E�E + F(3) + F(2)
�@�����ŁAF(2)=F(1)�ł�����A�����Q�͐��藧���܂��B
�y�����R�z
�@��������l�ɂ���
�@�@F(2n+1) = F(2n) + F(2n-1)
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-3)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-4) + �E�E�E + F(2) + F(1)
�@�����ŁAF(1)=1�ł�����A�����R�͐��藧���܂��B
�y�����S�z
�@���[�����A�Q���������܂��ό`����Ƃł���(�H)��������܂��A�Z��
���Ȃ��̂ŏ�����蓹�����čl���܂����B
�@�܂��A�����ʂ̕�������l���āA���R��m�An�ɑ��āA
F(n) = F(m+1)F(n-m) + F(m)F(n-m-1) �E�E�E (1)
�@�����藧���Ƃ��m���߂܂��Bm�Ɋւ��鐔�w�I�A�[�@�ŏؖ����܂��B
�@m=1�̏ꍇ
�@F(n) = F(1+1)F(n-1) + F(1)F(n-1-1)
�@�@�@ = F(2)F(n-1) + F(1)F(n-2)
�@�@�@ = F(n-1) + F(n-2)
�@�ƂȂ萬�藧���܂��B
�Am=k�̂Ƃ�(1)������������Ƃ��āAm=k+1�̏ꍇ
�@������A
�@�@F(n) = F(k+1)F(n-k) + F(k)F(n-k-1)
�@�ł��B�����ό`���āA
�@�@F(n) = F(k+1){F(n-k-1) + F(n-k-2)} + F(k)F(n-k-1)
�@�@�@�@ = F(k+1)F(n-k-1) + F(k+1)F(n-k-2) + F(k)F(n-k-1)
�@�@�@�@ = {F(k+1) + F(k)}F(n-k-1) + F(k+1)F(n-k-2)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����A(1)����m=k+1��������
�@�@F(n) = F((k+1)+1)F(n-(k+1)) + F(k+1)F(n-(k+1)-1)
�@�@�@�@ = F(k+1+1)F(n-k-1) + F(k+1)F(n-k-1-1)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����āAm=k+1�̏ꍇ�����藧���܂��B
�B��L�@�A�A��肷�ׂĂ̎��R��m�An�ɑ��āA(1)�������藧���܂��B
�@���āA���Ȃ蓹�������Ă��܂��܂������A���������ł��B(1)�ɂ�����n��2n+1�A
m��n�Ƃ����
�@�@F(2n+1) = F(n+1)F(2n+1-n) + F(n)F(2n+1-n-1)
�@�@�@�@�@�@= F(n+1)^2 + F(n)^2
�@����āA�����S�͐��藧���܂��B
�y�����T�z
�@�����������蓹�����܂��B
�@�@F(i)F(i+1) = F(i){F(i-1)
+ F(i)} = F(i)F(i-1) + F(i)^2
�@�@�� F(i)^2 = F(i)F(i+1) -
F(i)F(i-1) �E�E�E(1)
�@(1)����i=2,3,�E�E�E,n�͈̔͂ʼn��Z�����
�@�@���� = F(2)^2 + F(3)^2 + �E�E�E + F(n)^2
�@�@�E�� = F(2)F(3) + F(3)F(4) + �E�E�E + F(n)F(n+1)
�@�@�@�@ - { F(2)F(1) + F(3)F(2) + �E�E�E + F(n)F(n-1) }
�@�@�@�@ = F(n)F(n+1) - F(2)F(1)
�@�܂�A
�@�@F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1) - F(2)F(1)
�@�ƂȂ�AF(2)=F(1)=F(1)^2�ɒ��ӂ���ƁA
�@�@F(1)^2 + F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1)
�@����āA�����T�͐��藧���܂��B
���R�����g�����āA���肸�ɑ�123����ɒ��킵�Ă݂܂����i��Ƃ𑝂₵�Ă��܂����Ƃ������ى������j�B
�@���̃t�B�{�i�b�`����̊W���͂悭�ڂɂ��܂����A�u�ؖ����Ă݂ĉ������v�ƌ�����ƁE�E�E���[��ƌ����������ł��ˁB�ł����Ƃ������t����]������
�ؖ���������ł��B��{�I�ɂ́A�R�c�R�c�Ɛ��w�I�A�[�@�ł��A���ׂďؖ��ł�����̂Ǝv���܂����A�����S�ȊO�͑Q������ό`���ďؖ����Ă݂܂����B
H
(Hn�|�d)
��
H
�{H2�{�E�E�E�{Hn-1
�g
��
��
-
1
�|
�P
�P
�P
�O
�O
�P
�P
�P
��
(
H�|�d)-1
H
2
��
�P
�P
�P
�Q
��
�{
�P
�O
�O
�P
�O
�P
�P
�P
��
H
�{�d
H
n+1
��
��
�e
n
�e
n+1
�e
n+1
�e
n+2
��
�e
n
F
n+1
F
n+Fn-1
F
n+Fn+1
�O
�P
�P
�P
��
�e
n-1
�e
n
�e
n
�e
n+1
H
n�E�g
��
�O
�P
�P
�P
�e
0
�e
1
�e
1
�e
2
��
H
��
H
n
�e
n-1
�e
n
�e
n

�F����A�l�������킩������A�S���łȂ��Ă����ł�����A�ƃy���l�[����Y���āA���[���ő����Ă��������B
�҂��Ă��܂��B
�m�n�P�uH7K�v���� 7/26:
10��34�� ��M �X�V8/17
�A�[�@�łȂ��Ă�������悤�ȋC�������ł���...
1: ��n=1,2�̂Ƃ�
�@�@1+F1=2=F3.����
1+F1+F2=3=F4.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�C1+F1+F2+...+Fk=F(k+2)�Ɖ��肷���
�@�@ ���ӂ�F(k+1)�𑫂��C1+F1+F2+...+Fk+F(k+1)=F(k+2)+F(k+1)=F(k+3)=F(k+1+2).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
2: ��n=1,2�̂Ƃ�
�@�@ F1=F2.����
�@�@ F1+F3=3=F4.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�CF1+F3+...+F(2k-1)=F(2k)�Ɖ��肷���
�@�@ ���ӂ�F(2k+1)�𑫂��CF1+F3+...+F(2k-1)+F(2k+1)=F(2k)+F(2k+1)=F(2k+2)
����F1+F3+...+F(2k-1)+F(2(k+1)-1)=F(2(k+1)).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
3: ��n=1,2�̂Ƃ�
�@�@1+F2=2=F3.����
1+F2+F4=5=F6.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�C1+F2+F4+...+F(2k)=F(2k+1)�Ɖ��肷���
�@�@ ���ӂ�F(2k+2)�𑫂��C1+F2+F4+...+F(2k)+F(2k+2)=F(2k+1)+F(2k+2)=F(2k+3)
����1+F2+F4+...+F(2k)+F(2(k+1))=F(2(k+1)+1)
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
4: �u�Δ�сv�ōl����D
�@�@O O O O ...O O O��2n+1���̐�����C������1,2,3,..,2n+1�̔ԍ����t���Ă���Ƃ���D
�@�@�����ŁC1��n�܂Ŕ�ԁi�A�������̂�1������̂݁j�Ƃ���ƁC���̏ꍇ�̒ʂ萔��F(n).
�@�@����C2n+1��ԏꍇ��
�@�@�En-1��n+1���ԁin�͒ʉ߁jF(n-1)F(2)F(n+1)=F(n-1)F(n+1)�ʂ�
�@�@�En���ԁc�cFnF(n+2)=Fn^2+Fn(Fn+1)�ʂ�
�@�@�Ȃ̂ŁC�vFn^2+(F(n-1)+Fn)F(n+1)=Fn^2+F(n-1)^2�ʂ肾���C�S�̂͂܂�F(2n+1)�ʂ�ł�����͂��C
�@�@����Ď����ꂽ�D
5: ��n=1,2�̂Ƃ�
�@ F1^2=1=F1F2.����
F1^2+F2^2=2=F2F3.����
��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@ �@���Ȃ킿�CF1^2+F2^2+...+Fk^2=FkF(k+1)�Ɖ��肷���
�@ �@���ӂ�F(k+1)^2�������CF1^2+F2^2+...+Fk^2+F(k+1)^2=FkF(k+1)+F(k+1)^2=F(k+2)F(k+1)=F(k+1)F(k+1+1).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
�m�n�Q�utoru�v����@�@�@7/29: 13��54�� ��M �X�V8/17
�P�DFn+2�\Fn+1��Fn �@�ɂ�����n=1,2,3,------,n�Ƃ��ĕӕӂ�������Fn+2�\F2��F1
�{F2�{F3�{-------�{Fn F2��1�����琫���P�����藧�B
�Q�DF2n+2�\F2n��F2n+1 (n=1,2,3----)��, F0��0�Ƃ����n=0�ł����藧����A
n=0,1,2,3,------,n-1 �Ƃ��ĕӕӂ�����F2n��F1�{F3�{F5�{---�{F2n-1
�R�D F2n+1�\F2n-1��F2n �ɂ�����n=1,2,3,------,n�Ƃ��ĕӕӂ�������F2n+1�\F1
��F2�{F4�{F6�{-------�{F2n, F1��1�����琫��3�����藧�B
�S�D F2n��2FnFn+1�\Fn^2, F2n+1��Fn^2�{Fn+1^2�Ɖ��肵�Đ��w�I�A�[�@�ŏؖ�����A
n=1�̂Ƃ�F2=2F1F2�\F1^2��1,F3=F1^2�{F2^2��2,�Ő��藧�An=n+1�Ƃ��āAF2n+2
��F2n�{F2n+1��(2FnFn+1�\Fn^2)�{(Fn^2�{Fn+1^2)��2FnFn+1�{Fn+1^2��2(Fn+2
�\Fn+1)Fn+1�{Fn+1^2��2Fn+1Fn+2�\Fn+1^2, F2n+3��F2n+1�{F2n+2��(Fn^2�{Fn+1^2)
�{(2Fn+1Fn+2�\Fn+1^2)��Fn^2�{2Fn+1Fn+2��(Fn+2�\Fn+1)^2�{2Fn+1Fn+2��Fn+1^2
�{Fn+2^2 ��萫���S�͏ؖ����ꂽ�B
�T�DFn+1Fn+2�\FnFn+1��Fn+1(Fn+Fn+1)�\FnFn+1=Fn+1^2 �ɂ�����F0=0 �Ƃ������
��n=0�ł����藧����n=0,1,2,---n-1�Ƃ��ĕӕӂ����AFnFn+1��F1^2�{F2^2
�{F3^2�{-------�{Fn^2
���R�����g�������P�A�Q�A�R�A�T�����w�I�A�[�@���g���ΊȒP�ɏؖ��ł��܂����A�ǂ�������^�����Ċm���߂Ă��邾���̂悤�ŋC�ɓ���Ȃ��̂ŁA�Ȃ�ł���Ȏ����o�Ă���̂��l�����ł��A���ړ����Ă݂܂����B�Ƃ��낪�A�ǂ����S�͂��܂��s�����Ɍ��NjA�[�@���g������ɂ��܂�X�}�[�g�łȂ��ɂȂ��Ă��܂��܂����B�����ƁA�����ƃG
���K���g�ȕ��@������̂ł��傤���A�Ȃ��Ȃ����Ԃ��Ƃꂸ�A��肠�������𑗂��Ă����܂��B�@
�utoru�v���� 8/01: 11��07��
��M �X�V8/17
�t�B�{�i�b�`����F0=0,F1=1,Fn+2=Fn+1+Fn (n=0,1,2---)�̈�ʍ���x^2-x-1=0�̂Q��
�����A��(��<��)�Ƃ���� ���{��=1,����=-1�� Fn=(��^n�\��^n)�^(���\��)�@
������(��^(2n+1)�\��^(2n+1))(���\��)����^2(n+1)�{��^2(n+1)�{��^(2n)�{��^(2n)
��(��^n�{��^n)^2�{(��^(n+1)�{��^(n+1))^2�����藧����A���ӂ�(���\��)^2�Ŋ�
��AF2n+1��Fn^2�{Fn+1^2�����藧���Ƃ�������܂��B�����Ń���=-1�͎g���Ă�
�܂����A���{��=1�̕��͎g���Ă��܂���̂ŁA���̊W��F0=0,F1=1,Fn+2=kFn+1+Fn
�ł����藧�Ǝv���܂��B�Ⴆ��k���Q�Ƃ���ƁA���̐���
��(0),1,2,5,12,29,70,169,408,985,2378,5741,-----�ƂȂ�܂����A1^2+2^2=5,
2^2+5^2=29, 5^2+12^2=169 �Ƃ����悤�Ȋ����Ő��藧���Ă��܂��B
���R�����g�������S�ɂ��ĕʉ�������Ă݂܂����B��ʉ������߂Ă��育��v�Z����̂͂ǂ����Ƃ��v���܂������A����Ă݂�Ƃ��̖��Ɋւ��Ă͂��̕����悢���ƁH�A�ǂ�Ȃ���ł��傤�B
�m�n�R�ukasama�v����@ 7/29: 23��01�� ��M �X�V8/17
�y�����P�z
�@�Q������K���ɑ��삷��Əo�������ł��ˁB�Q���������Ԃɕ��ׂĂ݂�ƁA
�@�@F(n) + F(n+1) = F(n+2)
�@�@F(n-1) + F(n) = F(n+1)
�@�@F(n-2) + F(n-1) = F(n)
�@�@�@�@�@�E�E�E
�@�@F(1) + F(2) = F(3)�@�ƂȂ�܂��B�����̎������Z�����
�@2�~{F(1)+F(2)+�E�E�E+F(n)} - F(1) + F(n+1) =
�@�@ {F(1)+F(2)+�E�E�E+F(n)} - F(1) - F(2) + F(n+1) + F(n+2)
�@�� F(1)+F(2)+�E�E�E+F(n) = F(n+2) - F(2)
�@�ƂȂ�܂��B�����ŁAF(2)=1�ł����琫���P�͐��藧���܂��B�ȉ��̐����Q�A�R���瓱�����Ƃ��ł���Ǝv���܂��B�ł����Ԓʂ�ɁI
�y�����Q�z
�@������Q������K���ɑ��삷��Əo�������ł��ˁB
�@�@F(2n) = F(2n-1) + F(2n-2)
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-4)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-5) + �E�E�E + F(3) + F(2)
�@�����ŁAF(2)=F(1)�ł�����A�����Q�͐��藧���܂��B
�y�����R�z
�@��������l�ɂ���
�@�@F(2n+1) = F(2n) + F(2n-1)
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-3)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-4) + �E�E�E + F(2) + F(1)
�@�����ŁAF(1)=1�ł�����A�����R�͐��藧���܂��B
�y�����S�z
�@���[�����A�Q���������܂��ό`����Ƃł���(�H)��������܂��A�Z�ʂ��Ȃ��̂ŏ�����蓹�����čl���܂����B
�@�܂��A�����ʂ̕�������l���āA���R��m�An�ɑ��āA
F(n) = F(m+1)F(n-m) + F(m)F(n-m-1) �E�E�E (1)
�@�����藧���Ƃ��m���߂܂��Bm�Ɋւ��鐔�w�I�A�[�@�ŏؖ����܂��B
�@m=1�̏ꍇ
�@F(n) = F(1+1)F(n-1) + F(1)F(n-1-1)
�@�@�@ = F(2)F(n-1) + F(1)F(n-2)
�@�@�@ = F(n-1) + F(n-2)
�@�ƂȂ萬�藧���܂��B
�Am=k�̂Ƃ�(1)������������Ƃ��āAm=k+1�̏ꍇ
�@������A
�@�@F(n) = F(k+1)F(n-k) + F(k)F(n-k-1)
�@�ł��B�����ό`���āA
�@�@F(n) = F(k+1){F(n-k-1) + F(n-k-2)} + F(k)F(n-k-1)
�@�@�@�@ = F(k+1)F(n-k-1) + F(k+1)F(n-k-2) + F(k)F(n-k-1)
�@�@�@�@ = {F(k+1) + F(k)}F(n-k-1) + F(k+1)F(n-k-2)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����A(1)����m=k+1��������
�@�@F(n) = F((k+1)+1)F(n-(k+1)) + F(k+1)F(n-(k+1)-1)
�@�@�@�@ = F(k+1+1)F(n-k-1) + F(k+1)F(n-k-1-1)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����āAm=k+1�̏ꍇ�����藧���܂��B
�B��L�@�A�A��肷�ׂĂ̎��R��m�An�ɑ��āA(1)�������藧���܂��B
�@���āA���Ȃ蓹�������Ă��܂��܂������A���������ł��B(1)�ɂ�����n��2n+1�Am��n�Ƃ����
�@�@F(2n+1) = F(n+1)F(2n+1-n) + F(n)F(2n+1-n-1)
�@�@�@�@�@�@= F(n+1)^2 + F(n)^2
�@����āA�����S�͐��藧���܂��B
�y�����T�z
�@�����������蓹�����܂��B
�@�@F(i)F(i+1) = F(i){F(i-1)
+ F(i)} = F(i)F(i-1) +
F(i)^2
�@�@�� F(i)^2 = F(i)F(i+1)
- F(i)F(i-1) �E�E�E(1)
�@(1)����i=2,3,�E�E�E,n�͈̔͂ʼn��Z�����
�@�@���� = F(2)^2 + F(3)^2 + �E�E�E + F(n)^2
�@�@�E�� = F(2)F(3) + F(3)F(4) + �E�E�E + F(n)F(n+1)
�@�@�@�@ - { F(2)F(1) + F(3)F(2) + �E�E�E + F(n)F(n-1) }
�@�@�@�@ = F(n)F(n+1) - F(2)F(1)
�@�܂�A
�@�@F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1) - F(2)F(1)
�@�ƂȂ�AF(2)=F(1)=F(1)^2�ɒ��ӂ���ƁA
�@�@F(1)^2 + F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1)
�@����āA�����T�͐��藧���܂��B
���R�����g�����āA���肸�ɑ�123����ɒ��킵�Ă݂܂����i��Ƃ𑝂₵�Ă��܂����Ƃ������ى������j�B
�@���̃t�B�{�i�b�`����̊W���͂悭�ڂɂ��܂����A�u�ؖ����Ă݂ĉ������v�ƌ�����ƁE�E�E���[��ƌ����������ł��ˁB�ł����Ƃ������t����]�����ďؖ��������肷�B��{�I�ɂ́A�R�c�R�c�Ɛ��w�I�A�[�@�ł��A���ׂďؖ��ł�����̂Ǝv���܂����A�����S�ȊO�͑Q������ό`���ďؖ����Ă݂܂����B
�ukasama�v���� 8/01: 22��41�� ��M �X�V817
�y�����z
�@�O��̖��ł͍s�i����͑�w�ŏK���j���g���Ă��܂��܂������A����͍��Z���w�ŏK���s��𗘗p���܂��B�����Ȃ�ؖ�����̂͑�ςȂ̂ŏ��������̑������Ă����܂��B
�܂��A�t�B�{�i�b�`������ȉ��̂悤�ȍs��ŕ\�����܂��B
|
|
�uKasama�v���� 8/01: 22��41�� ��M �X�V8/17
�y�����z
�@�O��̖��ł͍s�i����͑�w�ŏK���j���g���Ă��܂��܂������A����͍��Z���w�ŏK���s��𗘗p���܂��B�����Ȃ�ؖ�����̂͑�ςȂ̂ŏ��������̑������Ă����܂��B
�܂��A�t�B�{�i�b�`������ȉ��̂悤�ȍs��ŕ\�����܂��B
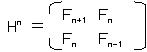
���ɁA�����P�̏ꍇ��
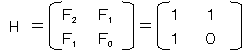
�ŁAF0=0�Ɩ��Ă����܂��B����ƁA
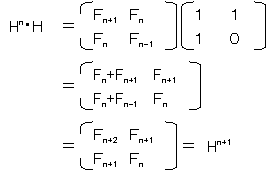
���l�ɁA�g�EHn��Hn+1�ł��B
�܂��AE��P�ʍs��Ƃ��āA
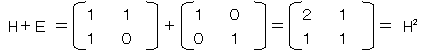
�ł�����A���ӂ���Hn-1���|����ƁA
�@Hn�{Hn-1��Hn+1
�ł��B����ɁA
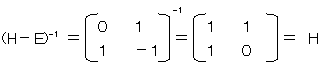
�ł��B�ȏ�ŏ��������I
�y�����P�z
�܂��A���䐔��̌�������
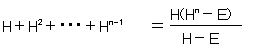
�ł��B(H�{�d)-1���g�ł�����A�E�Ӂ�H2(Hn�|�d)��Hn+2�|H�ƂȂ�A
�@H�{H2�{�E�E�E�{Hn-1��Hn+2�|H
�ł��B�s���2�s1��ڂ̗v�f�ɒ��ڂ���ƁA
�@F1�{F2�{�E�E�E�{Fn��Fn+2�|1
�ƂȂ��Ă��܂��ˁB
���R�����g����������肵���ؖ������������ǂ��������ȂƂ���A���M������܂��A�ʔ����������Ă��邱�Ƃ͎����ł��ˁB
�@�����ʂ̊p�x������g�����Ƃ��Ă��܂��B�s��ƊW�t���ďؖ����悤���ȂƂ��Ă��܂��B�������A�Ώۂ����Z�P�N���ƕ����Ă���̂ŁA�ǂ̒��x���w�܂łȂ�m���Ă���̂��悭����܂���B�T�x�Q�����ȂǂŁA�������Z�����������Ƒ啪�l�q������Ă���悤�ȋC�����܂��E�E�E
�@�Y�t���X�g�ɐ����P�����̏ؖ����L�ڂ��܂����B���̂悤�ȕ��@�ł͂������Ȃ��̂ł��傤���H
H
(Hn�|�d)
��
H
�{H2�{�E�E�E�{Hn-1
�g
��
��
-
1
�|
�P
�P
�P
�O
�O
�P
�P
�P
��
(
H�|�d)-1
H
2
��
�P
�P
�P
�Q
��
�{
�P
�O
�O
�P
�O
�P
�P
�P
��
H
�{�d
H
n+1
��
��
�e
n
�e
n+1
�e
n+1
�e
n+2
��
�e
n
F
n+1
F
n+Fn-1
F
n+Fn+1
�O
�P
�P
�P
��
�e
n-1
�e
n
�e
n
�e
n+1
H
n�E�g
��
�O
�P
�P
�P
�e
0
�e
1
�e
1
�e
2
��
H
��
H
n
�e
n-1
�e
n
�e
n

�F����A�l�������킩������A�S���łȂ��Ă����ł�����A�ƃy���l�[����Y���āA���[���ő����Ă��������B
�҂��Ă��܂��B
�m�n�P�uH7K�v���� 7/26:
10��34�� ��M �X�V8/17
�A�[�@�łȂ��Ă�������悤�ȋC�������ł���...
1: ��n=1,2�̂Ƃ�
�@�@1+F1=2=F3.����
1+F1+F2=3=F4.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�C1+F1+F2+...+Fk=F(k+2)�Ɖ��肷���
�@�@ ���ӂ�F(k+1)�𑫂��C1+F1+F2+...+Fk+F(k+1)=F(k+2)+F(k+1)=F(k+3)=F(k+1+2).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
2: ��n=1,2�̂Ƃ�
�@�@ F1=F2.����
�@�@ F1+F3=3=F4.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�CF1+F3+...+F(2k-1)=F(2k)�Ɖ��肷���
�@�@ ���ӂ�F(2k+1)�𑫂��CF1+F3+...+F(2k-1)+F(2k+1)=F(2k)+F(2k+1)=F(2k+2)
����F1+F3+...+F(2k-1)+F(2(k+1)-1)=F(2(k+1)).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
3: ��n=1,2�̂Ƃ�
�@�@1+F2=2=F3.����
1+F2+F4=5=F6.����
�@ ��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@�@ ���Ȃ킿�C1+F2+F4+...+F(2k)=F(2k+1)�Ɖ��肷���
�@�@ ���ӂ�F(2k+2)�𑫂��C1+F2+F4+...+F(2k)+F(2k+2)=F(2k+1)+F(2k+2)=F(2k+3)
����1+F2+F4+...+F(2k)+F(2(k+1))=F(2(k+1)+1)
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
4: �u�Δ�сv�ōl����D
�@�@O O O O ...O O O��2n+1���̐�����C������1,2,3,..,2n+1�̔ԍ����t���Ă���Ƃ���D
�@�@�����ŁC1��n�܂Ŕ�ԁi�A�������̂�1������̂݁j�Ƃ���ƁC���̏ꍇ�̒ʂ萔��F(n).
�@�@����C2n+1��ԏꍇ��
�@�@�En-1��n+1���ԁin�͒ʉ߁jF(n-1)F(2)F(n+1)=F(n-1)F(n+1)�ʂ�
�@�@�En���ԁc�cFnF(n+2)=Fn^2+Fn(Fn+1)�ʂ�
�@�@�Ȃ̂ŁC�vFn^2+(F(n-1)+Fn)F(n+1)=Fn^2+F(n-1)^2�ʂ肾���C�S�̂͂܂�F(2n+1)�ʂ�ł�����͂��C
�@�@����Ď����ꂽ�D
5: ��n=1,2�̂Ƃ�
�@ F1^2=1=F1F2.����
F1^2+F2^2=2=F2F3.����
��n=k�̂Ƃ��C�������Ă���Ɖ���C
�@ �@���Ȃ킿�CF1^2+F2^2+...+Fk^2=FkF(k+1)�Ɖ��肷���
�@ �@���ӂ�F(k+1)^2�������CF1^2+F2^2+...+Fk^2+F(k+1)^2=FkF(k+1)+F(k+1)^2=F(k+2)F(k+1)=F(k+1)F(k+1+1).
�@�@ ����āCn=k+1�̏ꍇ���������邱�Ƃ�������D//
�m�n�Q�utoru�v����@�@�@7/29: 13��54�� ��M �X�V8/17
�P�DFn+2�\Fn+1��Fn �@�ɂ�����n=1,2,3,------,n�Ƃ��ĕӕӂ�������Fn+2�\F2��F1
�{F2�{F3�{-------�{Fn F2��1�����琫���P�����藧�B
�Q�DF2n+2�\F2n��F2n+1 (n=1,2,3----)��, F0��0�Ƃ����n=0�ł����藧����A
n=0,1,2,3,------,n-1 �Ƃ��ĕӕӂ�����F2n��F1�{F3�{F5�{---�{F2n-1
�R�D F2n+1�\F2n-1��F2n �ɂ�����n=1,2,3,------,n�Ƃ��ĕӕӂ�������F2n+1�\F1
��F2�{F4�{F6�{-------�{F2n, F1��1�����琫��3�����藧�B
�S�D F2n��2FnFn+1�\Fn^2, F2n+1��Fn^2�{Fn+1^2�Ɖ��肵�Đ��w�I�A�[�@�ŏؖ�����A
n=1�̂Ƃ�F2=2F1F2�\F1^2��1,F3=F1^2�{F2^2��2,�Ő��藧�An=n+1�Ƃ��āAF2n+2
��F2n�{F2n+1��(2FnFn+1�\Fn^2)�{(Fn^2�{Fn+1^2)��2FnFn+1�{Fn+1^2��2(Fn+2
�\Fn+1)Fn+1�{Fn+1^2��2Fn+1Fn+2�\Fn+1^2, F2n+3��F2n+1�{F2n+2��(Fn^2�{Fn+1^2)
�{(2Fn+1Fn+2�\Fn+1^2)��Fn^2�{2Fn+1Fn+2��(Fn+2�\Fn+1)^2�{2Fn+1Fn+2��Fn+1^2
�{Fn+2^2 ��萫���S�͏ؖ����ꂽ�B
�T�DFn+1Fn+2�\FnFn+1��Fn+1(Fn+Fn+1)�\FnFn+1=Fn+1^2 �ɂ�����F0=0 �Ƃ������
��n=0�ł����藧����n=0,1,2,---n-1�Ƃ��ĕӕӂ����AFnFn+1��F1^2�{F2^2
�{F3^2�{-------�{Fn^2
���R�����g�������P�A�Q�A�R�A�T�����w�I�A�[�@���g���ΊȒP�ɏؖ��ł��܂����A�ǂ�������^�����Ċm���߂Ă��邾���̂悤�ŋC�ɓ���Ȃ��̂ŁA�Ȃ�ł���Ȏ����o�Ă���̂��l�����ł��A���ړ����Ă݂܂����B�Ƃ��낪�A�ǂ����S�͂��܂��s�����Ɍ��NjA�[�@���g������ɂ��܂�X�}�[�g�łȂ��ɂȂ��Ă��܂��܂����B�����ƁA�����ƃG
���K���g�ȕ��@������̂ł��傤���A�Ȃ��Ȃ����Ԃ��Ƃꂸ�A��肠�������𑗂��Ă����܂��B�@
�utoru�v���� 8/01: 11��07��
��M �X�V8/17
�t�B�{�i�b�`����F0=0,F1=1,Fn+2=Fn+1+Fn (n=0,1,2---)�̈�ʍ���x^2-x-1=0�̂Q��
�����A��(��<��)�Ƃ���� ���{��=1,����=-1�� Fn=(��^n�\��^n)�^(���\��)�@
������(��^(2n+1)�\��^(2n+1))(���\��)����^2(n+1)�{��^2(n+1)�{��^(2n)�{��^(2n)
��(��^n�{��^n)^2�{(��^(n+1)�{��^(n+1))^2�����藧����A���ӂ�(���\��)^2�Ŋ�
��AF2n+1��Fn^2�{Fn+1^2�����藧���Ƃ�������܂��B�����Ń���=-1�͎g���Ă�
�܂����A���{��=1�̕��͎g���Ă��܂���̂ŁA���̊W��F0=0,F1=1,Fn+2=kFn+1+Fn
�ł����藧�Ǝv���܂��B�Ⴆ��k���Q�Ƃ���ƁA���̐���
��(0),1,2,5,12,29,70,169,408,985,2378,5741,-----�ƂȂ�܂����A1^2+2^2=5,
2^2+5^2=29, 5^2+12^2=169 �Ƃ����悤�Ȋ����Ő��藧���Ă��܂��B
���R�����g�������S�ɂ��ĕʉ�������Ă݂܂����B��ʉ������߂Ă��育��v�Z����̂͂ǂ����Ƃ��v���܂������A����Ă݂�Ƃ��̖��Ɋւ��Ă͂��̕����悢���ƁH�A�ǂ�Ȃ���ł��傤�B
�m�n�R�ukasama�v����@ 7/29: 23��01�� ��M �X�V8/17
�y�����P�z
�@�Q������K���ɑ��삷��Əo�������ł��ˁB�Q���������Ԃɕ��ׂĂ݂�ƁA
�@�@F(n) + F(n+1) = F(n+2)
�@�@F(n-1) + F(n) = F(n+1)
�@�@F(n-2) + F(n-1) = F(n)
�@�@�@�@�@�E�E�E
�@�@F(1) + F(2) = F(3)�@�ƂȂ�܂��B�����̎������Z�����
�@2�~{F(1)+F(2)+�E�E�E+F(n)} - F(1) + F(n+1) =
�@�@ {F(1)+F(2)+�E�E�E+F(n)} - F(1) - F(2) + F(n+1) + F(n+2)
�@�� F(1)+F(2)+�E�E�E+F(n) = F(n+2) - F(2)
�@�ƂȂ�܂��B�����ŁAF(2)=1�ł����琫���P�͐��藧���܂��B�ȉ��̐����Q�A�R���瓱�����Ƃ��ł���Ǝv���܂��B�ł����Ԓʂ�ɁI
�y�����Q�z
�@������Q������K���ɑ��삷��Əo�������ł��ˁB
�@�@F(2n) = F(2n-1) + F(2n-2)
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-4)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@= F(2n-1) + F(2n-3) + F(2n-5) + �E�E�E + F(3) + F(2)
�@�����ŁAF(2)=F(1)�ł�����A�����Q�͐��藧���܂��B
�y�����R�z
�@��������l�ɂ���
�@�@F(2n+1) = F(2n) + F(2n-1)
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-3)
�@�@�@�@�E�E�E�E�E
�@�@�@�@�@�@= F(2n) + F(2n-2) + F(2n-4) + �E�E�E + F(2) + F(1)
�@�����ŁAF(1)=1�ł�����A�����R�͐��藧���܂��B
�y�����S�z
�@���[�����A�Q���������܂��ό`����Ƃł���(�H)��������܂��A�Z�ʂ��Ȃ��̂ŏ�����蓹�����čl���܂����B
�@�܂��A�����ʂ̕�������l���āA���R��m�An�ɑ��āA
F(n) = F(m+1)F(n-m) + F(m)F(n-m-1) �E�E�E (1)
�@�����藧���Ƃ��m���߂܂��Bm�Ɋւ��鐔�w�I�A�[�@�ŏؖ����܂��B
�@m=1�̏ꍇ
�@F(n) = F(1+1)F(n-1) + F(1)F(n-1-1)
�@�@�@ = F(2)F(n-1) + F(1)F(n-2)
�@�@�@ = F(n-1) + F(n-2)
�@�ƂȂ萬�藧���܂��B
�Am=k�̂Ƃ�(1)������������Ƃ��āAm=k+1�̏ꍇ
�@������A
�@�@F(n) = F(k+1)F(n-k) + F(k)F(n-k-1)
�@�ł��B�����ό`���āA
�@�@F(n) = F(k+1){F(n-k-1) + F(n-k-2)} + F(k)F(n-k-1)
�@�@�@�@ = F(k+1)F(n-k-1) + F(k+1)F(n-k-2) + F(k)F(n-k-1)
�@�@�@�@ = {F(k+1) + F(k)}F(n-k-1) + F(k+1)F(n-k-2)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����A(1)����m=k+1��������
�@�@F(n) = F((k+1)+1)F(n-(k+1)) + F(k+1)F(n-(k+1)-1)
�@�@�@�@ = F(k+1+1)F(n-k-1) + F(k+1)F(n-k-1-1)
�@�@�@�@ = F(k+2)F(n-k-1) + F(k+1)F(n-k-2)
�@����āAm=k+1�̏ꍇ�����藧���܂��B
�B��L�@�A�A��肷�ׂĂ̎��R��m�An�ɑ��āA(1)�������藧���܂��B
�@���āA���Ȃ蓹�������Ă��܂��܂������A���������ł��B(1)�ɂ�����n��2n+1�Am��n�Ƃ����
�@�@F(2n+1) = F(n+1)F(2n+1-n) + F(n)F(2n+1-n-1)
�@�@�@�@�@�@= F(n+1)^2 + F(n)^2
�@����āA�����S�͐��藧���܂��B
�y�����T�z
�@�����������蓹�����܂��B
�@�@F(i)F(i+1) = F(i){F(i-1)
+ F(i)} = F(i)F(i-1) +
F(i)^2
�@�@�� F(i)^2 = F(i)F(i+1)
- F(i)F(i-1) �E�E�E(1)
�@(1)����i=2,3,�E�E�E,n�͈̔͂ʼn��Z�����
�@�@���� = F(2)^2 + F(3)^2 + �E�E�E + F(n)^2
�@�@�E�� = F(2)F(3) + F(3)F(4) + �E�E�E + F(n)F(n+1)
�@�@�@�@ - { F(2)F(1) + F(3)F(2) + �E�E�E + F(n)F(n-1) }
�@�@�@�@ = F(n)F(n+1) - F(2)F(1)
�@�܂�A
�@�@F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1) - F(2)F(1)
�@�ƂȂ�AF(2)=F(1)=F(1)^2�ɒ��ӂ���ƁA
�@�@F(1)^2 + F(2)^2 + F(3)^2 + �E�E�E + F(n)^2 = F(n)F(n+1)
�@����āA�����T�͐��藧���܂��B
���R�����g�����āA���肸�ɑ�123����ɒ��킵�Ă݂܂����i��Ƃ𑝂₵�Ă��܂����Ƃ������ى������j�B
�@���̃t�B�{�i�b�`����̊W���͂悭�ڂɂ��܂����A�u�ؖ����Ă݂ĉ������v�ƌ�����ƁE�E�E���[��ƌ����������ł��ˁB�ł����Ƃ������t����]�����ďؖ��������肷�B��{�I�ɂ́A�R�c�R�c�Ɛ��w�I�A�[�@�ł��A���ׂďؖ��ł�����̂Ǝv���܂����A�����S�ȊO�͑Q������ό`���ďؖ����Ă݂܂����B
�ukasama�v���� 8/01: 22��41�� ��M �X�V817
�y�����z
�@�O��̖��ł͍s�i����͑�w�ŏK���j���g���Ă��܂��܂������A����͍��Z���w�ŏK���s��𗘗p���܂��B�����Ȃ�ؖ�����̂͑�ςȂ̂ŏ��������̑������Ă����܂��B
�܂��A�t�B�{�i�b�`������ȉ��̂悤�ȍs��ŕ\�����܂��B
|
|
�uKasama�v���� 8/07: 23��47�� ��M �X�V8/17
�y�����z
�@���Z�Q�`�R�ŏK���s��𗘗p���܂��B�ƌ����Ă����܂�[���K��Ȃ��悤�Ȃ̂ŁA�܂��A����Ȃ���������Ȃ��`�ƌ������x�ɂ݂Ă��炦��ƗL���ł��B�����Ȃ�ؖ�����̂͑�ςȂ̂ŏ��������̑������Ă����܂��B
�܂��A�t�B�{�i�b�`������ȉ��̂悤�ȍs��ŕ\�����܂��B
�@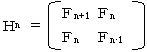
���ɁA�����P�̏ꍇ��
�@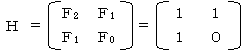
�ŁA�e0��0�Ɩ��Ă����܂��B����ƁA
�@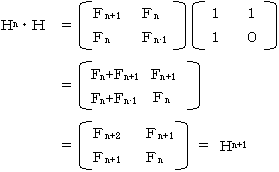
���l�ɁA�g�E�gn���gn+1�ł��B
�܂��A�d��P�ʍs��Ƃ��āA
�@
�ł�����A���ӂ���gn-1���|����ƁA
�@�gn�{�gn-1���gn+1
�ł��B����ɁA
�@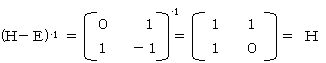
�ł��B�ȏ�łЂƂ܂����������I
�y�����P�z
�܂��A���䐔��̌�������
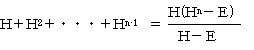
�ł��B�����ŁA(�g�{�d)-1���g�ł�����A�E�Ӂ��g2(�gn�|�d)���gn+2�|�g�ƂȂ�A
�@�g�{�g2�{�E�E�E�{�gn-1���gn+2�|�g
�ł��B�s���2�s1��ڂ̗v�f�ɒ��ڂ���ƁA
�@�e1�{�e2�{�E�E�E�{�en���en+2�|1
�ƂȂ��Ă��܂��ˁB
�y�����Q�z
������A���䐔��̌�������
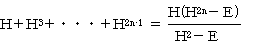
�ł��B�g�{�d= �g2�˂g2�|�d���g�ł�����A
�@�g�{�g3�{�E�E�E�{�g2n-1���g2n�|�d
�ł��B�s���2�s1��ڂ̗v�f�ɒ��ڂ���ƁA
�@�e1�{�e3�{�E�E�E�{�e2n-1���e2n
�ł��B
�y�����R�z
������A���䐔��̌�������
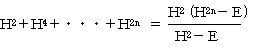
�܂�A�y�����Q�z�ł�����悤�ɁA�g2�|�d���g�ł�����A
�@�g2�{�g4�{�E�E�E�{�g2n���g2n+1�|�g�@�E�E�E(1)
�ł��B�s���2�s1��ڂ̗v�f�ɒ��ڂ���ƁA
�@�e2�{�e4�{�E�E�E�{�e2n���e2n+1�|�P
�ł��B
�@
�y�����S�z
�܂��A
�@�g2n+1���gn+1�E�gn�@�E�E�E(2)
�ł��BH2n+1�̗v�f���s��ŕ\������ƁA
�@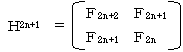
�܂��A�gn+1�E�gn�ɂ��Ă����l�ɂ��āA
�@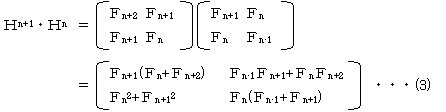
�ł��B�g2n+1�Ƃgn+1�E�gn�̂Q�s�P��ڂ̗v�f���r����ƁA
�@�en2+�en+12���e2n+1
�ł��B
�@
�y�����T�z
�@�y�����R�z��(1)�����y�����S�z��(2)���Ń`���b�g�ό`���܂��B
�@�g2�{�g4�{�E�E�E�{�g2n���g2n+1�|�g
�˂g��g�{�g2��g2�{�E�E�E�{�gn��gn���gn+1�E�gn�|�g
�gn��gn�̗v�f���s��ŕ\������ƁA
�@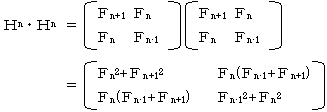
���l�ɁA�gn+1�E�gn�|�g�̗v�f���s��ŕ\������Ɓi�y�����S�z��(3)���Ōv�Z�������ʂ����p���܂��j�A
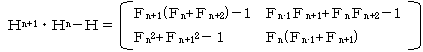
�ł��B�g��g�{�g2��g2�{�E�E�E�{�gn��gn�Ƃgn+1�E�gn�|�g�̂Q�s�Q��ڂ̗v�f���r����ƁA
�@(�e02+�e12)�{(�e12+�e22)�{����{(�en-12+�en2)���en(�en-1�{�en+1)
�˂e02�{2(�e12�{�e22�{����{�en2)�|�en2���en(�en-1�{�en+1)
�˂e02�{2(�e12�{�e22�{����{�en2)���en(�en-1�{�en�{�en+1)
�����ŁA�e0��0�A�en-1�{�en���en+1�Ȃ̂ŁA
��2(�e12�{�e22�{����{�en2)���en(�en+1�{�en+1)��2�en�en+1
�˂e12�{�e22�{����{�en2���en�en+1
�ƂȂ�܂��B
���R�����g�����āA�����x�̒��͌��Ă����Ȃ���Ȃ�Ƃ������܂��A�Ƃ肠�����A�s��𗘗p�����ؖ���������v���܂��B���Z���P�N���ɂƂ��āA���܂�ǂ������ł͂���܂���̂ŁA�Q�l���x�Ɉ����Ă��炦����ǂ��̂ł͂Ȃ����Ǝv���܂��B
�@�@�@�@������@�@mizuryu@aqua.ocn.ne.jp


 [���ꐯ]
[���ꐯ]

![]()
![]()
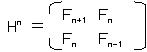
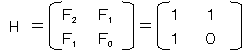
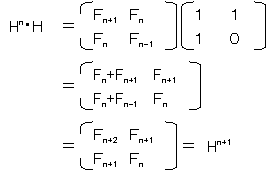
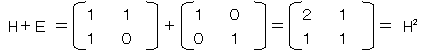
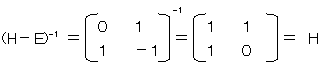
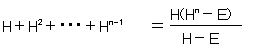
![]()
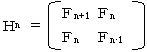
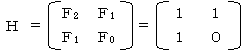
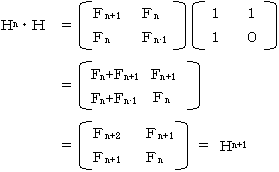

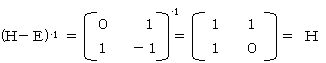
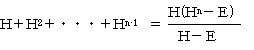
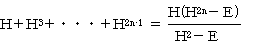
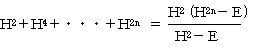
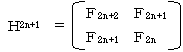
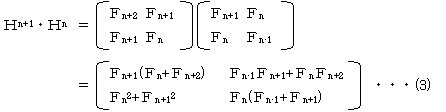
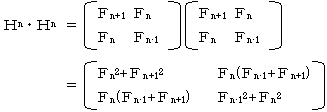
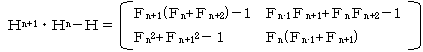
![]()
