平成15年9月7日
 [流れ星]
[流れ星]
第124回数学的な応募問題解答
<解答募集期間:8月17日~9月7日>
[指数型母関数]
太郎さんは、8月5日に全国算数・数学教育研究(愛知)大会に参加しました。このとき、2003年国際算数・数学能力検定ガイドという冊子をもらいました。この中で指数型母関数について、興味深い問題を見つけました。これを参考にして、今回は作成しました。皆さん!チャレンジください。

NO1「中川幸一」さん
8/17: 23時08分 受信 更新9/7

NO2「toru」さん 8/19: 16時19分 受信 更新9/7
第124回数学的応募問題に応募いたします。 添付ファイルは使っていませんので多分大丈夫かと思いますが、MACからなのでいつものように文字化けはあるやもし
れません。よろしくお願いします。
問題1~3 f(x)=e^(e^x-1)とするとf'(x)=e^x f(x),
f''(x)=(1e^x+1e^2x)f(x),
f'''(x)=(1e^x+3e^2x+1e^3x)f(x), f(4)(x)=((1e^x+7e^2x+6e^3x+1e^4x)f(x)
となって、第2種スターリング数があらわれる。数学的帰納法を使って、
f(n)(x)=(S(n,1)e^x+S(n,2)e^2x+-+S(n,k)e^kx+---+S(n,n)e^nx)f(x) ---(A)
(f(n)(x) はn回微分)が成り立つと仮定すると、
f(n+1)(x)=(S(n,1)e^x+2S(n,2)e^2x+-+kS(n,k)e^kx---+nS(n,n)e^nx)f(x)
+(S(n,1)e^x+S(n,2)e^2x+-+S(n,k)e^kx+---+S(n,n)e^nx)e^x f(x) から
S(n+1,k)=S(n,k-1)+kS(n,k),
S(n+1,1)=S(n,1)=1, S(n+1,S+1)=S(n,n)=1となり、
一般に成り立つことがわかる。f(n)(0)=S(n,1)+S(n,2)+----+S(n,n)=B(n)とすると、
f(x)のマクローリン展開、F(x)=1+B(1)x+B(2)/2!x^2+B(3)/3!x^3+--+B(n)/n!x^n+---
でa(n)=B(n)= S(n,1)+S(n+2)+-------+S(n,n) はベル数となる。
問題4 e^y=1+y+y^2/2+y^3/3!+---においてy=e^xとすると
f(x)=e^y/e=(1+e^x+e^2x/2+e^3x/3!+-----)/e これは項別に任意回微分できて、
f(n)(x)=(e^x+2^n/2 e^2x+3^n/3! e^3x+--+k^n/k! e^kx+---)/e ---(B) x=0とすれ
ば、a(n)=f(n)(0)=1/eΣk^n/k! (k=1~∞) が得られる。(k=0の時はk^n=0で同じ)
おまけ e^(-y)=1-y+y^2/2-y^3/3!+--------において、y=e^xとすることにより、
1/f(x)= e^(1-y) =e(1-e^x+e^2x/2-e^3x/3!+--------)が得られる。これと(B)を
かけ合わせると、おのおのは任意のxについて絶対収束で分配律が成り立つから、展
開できて、e^xの係数はΣ(-1)^r/r!・(k-r)^n/(k-r)!=Σ(-1)^r kCr (k-r)^n/k!
(r=0~k)、これをyについてのべき級数展開と考えれば、展開の仕方は一意であるか
ら、 (A)とくらべればこれがS(n,k)の一般項となる。
毎回面白い問題をありがとうございます。スターリング数、いつもながらこんなところにも出てくるのかと感動を覚えます。高校生のレベルでは、無限級数を項別に微
分してよいのか、無限級数どうしの積を有限級数と同様に展開してよいのかというところが疑問になると思われますが、(私は解析概論をチェックしてわかったつもり?)
高校生を相手にした時はどのように扱っておられるのでしょうか?(最近の高校生は解析概論ぐらい読んでいる?)
<水の流れコメント:うまくて凄い解答です。スムーズにいっています。感動しました。さて、最近の高校生は 解析概論はまだ、知りません。
ただ、優秀な私立の高校では、解析概論そのものは知らないけれども(私の推測)
無限級数を項別に微分してよいのか、無限級数どうしの積を有限級数と同様に展開してよいのかという質問ですが、
この点は 入試問題を解く中で、技法的に行っているでしょう。>
NO3「H7K」さん 8/20: 11時53分
受信 更新9/7
e^(e^x)=1+e^x/1!+e^{2x}/2!+e^{3x}/3!+e^{4x}/4!+...
=1+(1+x/1!+x^2/2!+x^3/3!+x^4/4!+...)/1!+(1+2x/1!+2^2x^2/2!+2^3x^3/3!+2^4x^4/4!+...)/2!+(1+3x/1!+3^2x^2/2!+3^3x^3/3!+3^4x^4/4!+...)/3!+(1+4x/1!+4^2x^2/2!+4^3x^3/3!+4^4x^4/4!+...)/4!+...
=(1+1/1!+1/2!+1/3!+....)+(1/1!+2/2!+3/3!+4/4!+...)x/1!+(1/1!+2^2/2!+3^2/3!+4^2/4!+...)x^2/2!+(1/1!+2^3/2!+3^3/3!+4^3/4!+...)x^3/3!+(1/1!+2^4/2!+3^4/3!+4^4/4!+...)x^4/4!+...
=sum{n=0 to inf.}sum{m=0 to inf.}{m^n/m! x^n/n!}.
g(k):=sum{m=1 to inf.}{m^k/m! x^{m-1}}とする.
すると,(x g(k))'=sum{m=0 to inf.}{m^{k+1}/m! x^{m-1}}=g(k+1)となる.
g(1)=e^xであることを考えると,g(2)=(x+1)e^x,g(3)=(x^2+3x+1)e^x,…となる.
すなわち.g(k)は,第2種Stirling数をS(n,k)を用いて,g(k)=e^x sum(n=1 to k){S(k,n)x^{n-1}}と書ける.
よって,
e^(e^x)=sum{n=0 to inf.}sum{m=0 to inf.}{m^n/m! x^n/n!}=sum{n=0 to
inf.}{g(n)(1)x^n/n!}.
=sum{n=0 to inf.}{e B(n) x^n/n!}.(B(n)はBell number.)
.
問題1:いまいち意味が良く分かりません.nCrとかを使って表せということでしょうか?
問題2:上より,a_n=B(n).(但し,a_0=1.) 具体的な値は,a_0=1, a_1=1,
a_2=2, a_3=5, …
問題3:ベル数.
問題4:上より明らか.//
NO4「kasama」さん 8/20: 23時53分 受信 更新9/7
さて、「第124回応募問題」についてです。第2種スターリング数について、先生のHPやその他文献で調査して、何とか回答できるレベルに達しました。前回
のフィボナッチ数列は結構ポピュラーな話題ですから、1から調べる必要はほとんどありませんでしたが、今回は見るものほとんどが新しいもので、問題を解く
というより勉強させて頂いたという方が適当だったと思います。専門家にとっては目新しいくはないでしょうけど、私にとっては新鮮な知識がたくさん詰まった
良いトピックでありました。
先生が教える生徒さんには、興味深い話題に出会える機会がたくさんあり、本当に羨ましい限りです。
問題1
n回微分を計算するのに少し工夫が必要ですね。f(x)=exp{ex-1}を直接微分するのは手間がかかるので、対数をとって
log{f(x)} = ex-1
と変形して微分すると、
f(x)(1)/f(x) = ex ⇒ f(x)(1) = exf(x)
となりますが、exは何回微分してもexですので有り難いですね。
Libnizの公式を利用して、上式をn回微分すると、
f(x)(n+1) = ∑nCr exf(x)(r)
(r=0,1,2,・・・,n)
f(0)(n+1) = ∑nCr f(0)(r) (r=0,1,2,・・・,n)
となります。ここで、f(0)=1です。先生が指示されている「指数型母関数」
(http://www2.ocn.ne.jp/~mizuryu/toukou/toukou18.html)の「分配の方法からの発見」の記載を参考にすると、上記の∑中のnCr f(0) (r)は第2種スターリン
グ数です(名前は聞いたことがありますが、内容はほんど理解していませんでした)。先生の記述ではS(n,r)と表されていましたので、この表記方法を利用
すると、F(x)つまりf(x)のマクローリン展開は
F(x) = ∑∑{S(k,r)}xk/k!
(内側r=0,1,2,・・・,n)、(外側k=0,1,2,・・・,∞) ・・・ (1) となります。
問題2、3
F(x)を指数型母関数とすると、一般項anは上記(1)式の内側の∑です。これは第2種スターリング数S(n,1)、S(n,2)、・・・S(n,n)の和ですが、「ベル指数の漸
化式の発見」によるとベル指数B(n)です。漸化式は「定理6」より
B(n+1) = ∑nCr B(r) (r=0,1,2,・・・,n)・・・ (2) で、{1,2,5,15,51,203,877,・・・}です。
問題4
一般項がベル指数なので、その漸化式を利用して、数学的帰納法で証明します。
①n=0の場合
B(0)=1
一方、
a0 = 1/e ∑k0/k! = e/e = 1
ですから、両者は等しいです。
②n≦rの場合
ar= B(r) = 1/e ∑kr/k!
(k=0,1,2,・・・,∞)
が成り立つと仮定します。
③n=r+1の場合
ar+1= B(r+1) =∑rCjB(j) (j=0,1,2,・・・,r)
= ∑rCj1/e∑kj/k! (内側k=0,1,2,・・・,∞)、(外側j=0,1,2,・・・,r)
=1/e∑1/k!∑rCjkj (内側k=0,1,2,・・・,∞)、(外側j=0,1,2,・・・,r) ←外側と内側の∑を入替え
= 1/e∑(k+1)r/k! (k=0,1,2,・・・,∞) ←二項定理の適用
= 1/e∑(k+1)r+1/(k+1)! (k=0,1,2,・・・,∞) ←分子、分母にk+1を掛ける
= 1/e∑kr+1/k! (k=0,1,2,・・・,∞)
①、②、③より
an= 1/e∑kn/k! (k=0,1,2,・・・,∞) が成り立ちます。
<水の流れコメント:この時期、添付ファイルが開けなくて、ご迷惑をおかけしていました。「kasama」さんにはお手数をおかけしたことをお許し下さい。>
NO5「UnderBird」さん 8/27: 13時59分 受信 更新9/7
第124回数学的な応募問題[指数型母関数]
《コメント》
問題1では、微分しても第n次導関数を導けず、GiveUpです。
もしかしたら具体的に数項求めるだけでよいのかしらとも勝手に思い込んで、ひたすら計算しました。
![]() となるので、
となるので、
![]()
・また、![]() を指数型母関数としたときの数列
を指数型母関数としたときの数列![]() は上の結果から
は上の結果から
![]() ですが、ここでも一般項は導けませんでした。
ですが、ここでも一般項は導けませんでした。
第18話 「第2種スターリング数S(n,k)」を参考に読もうとしましたが、
頭がついていかずこれもGiveUpです。
・
しかし、この中でこの数列が第2種スターリング数の和として定義されるベル指数と呼ばれるものであることがわかりました。
・最後の証明は、おそらく問題1~3までと、第18話の部分から導かれるのでしょうが、強引に導いてしまったような気がします。
では、問題4のみお願いいたします。
問題4の証明
![]() とおくと、
とおくと、![]() だから
だから
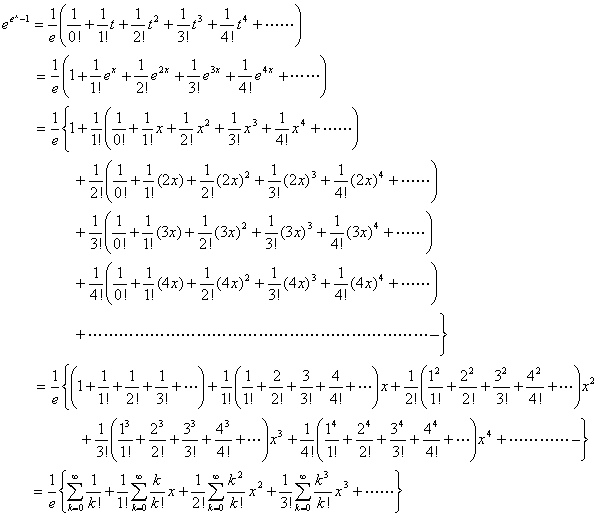
よって、![]() が成り立つ。 Q.E..D
が成り立つ。 Q.E..D
NO6「Kashiwagi」さん 8/29: 21時51分 受信 更新9/7
お世話になります。解答を送信させて頂きます。家庭のパソコンのため数学関連のソフトを入れておらず、非常に分かり難い答案になってしまい申し訳ございません。
大文字Xと小文字xで区分したつもりなのですが・・・・。それと問題4.は少々略
第124回
問1.
両辺の対数をとり、整理すると
![]()
![]() logf(x) = ex-1
両辺をxで微分すると、f’(x) = f(x)ex ①
logf(x) = ex-1
両辺をxで微分すると、f’(x) = f(x)ex ①
更に微分して、f’’(x) = ( f(x)+f’(x) )ex ②
![]() 更に微分して、f’’’(x) = ( f(x)+2f’(x) + f’’(x))ex ③
更に微分して、f’’’(x) = ( f(x)+2f’(x) + f’’(x))ex ③
以上と同様な操作を繰り返し、xに0を代入すると、
f(0) = 1, f’(0) = 1, f’’(0) = 2, f’’’(0) = 5, …………
以上より F(x) = 1 + x + x2 + (5/3!)x3 + (15/4!)x4 +…………・
問題2.
題意より求める数列は{1,1,2,5,15,…・・}
問題3.
ベル指数
問題4.
①
![]()
![]()
![]()
![]()
![]() 式のex = X ④ と置くと、
式のex = X ④ と置くと、
f(x) = G(X) = eX-1 ⑤
両辺をxで微分すると、f’(x) = (d G(X)/dX)(dX/dx)
⑤よりd G(X)/dX = eX-1 ⑥
④よりdX/dx = ex = X ⑦
因って、f’(x) = eX-1・X = (1/e) ex ・ X = (1/e)Σ(k=0…・・∞)Xk+1/k! ⑧
この両辺をxで更にn-1回微分する、但し、dX/dx = ex = Xを忘れずにかける、そして
xに0を代入するとそれがanであり、
f(n)(x) = an = (1/e)Σ(k=1…・・∞)kn-1/(k-1)!
ここで 分母、分子にkをかけて、
= (1/e)Σ(k=0…・・∞)kn/k! となる。
因って題意は証明された。
<水の流れコメント:皆さんがそれぞれ技法を駆使しながらの解答で、いずれにしても 第2種スターリング数やベル数の発見ができていました。>
![]()
