�����P�U�N�Q���P��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@�@�@�@��P�R�Q�����w�I�ȉ������No�Q
�@�@�@�@�@�@�@�@�@�@����W���ԁF�P���P�P���`�P���R�P����
�m�t�B�{�i�b�`���n
�@�@�@
�P�Q�O�Q�N�A�C�^���A�ɏZ��ł����t�B�{�i�b�`�͓����̑㐔�w�Ɛ����_�̒m���𑍍��������e�́u�Z�Ղ̏��v�Ƃ������̖{�����e����ŏo�ł��܂����B����͂P�O�i�@��p���Ċw�K���郈�[���[�p�ōŏ��̖{�̂P���ƂȂ�܂����B
�@�t�B�{�i�b�`�͓����̕��K�ł��������w���Z��i��������ō��E�ő��ʼn������J���Z�j�ɎQ�����܂����B�t�B�{�i�b�`�̖���������@�݂͂�Ȃ��������܂����B�t�B�{�i�b�`�̖����́A���w�O���[�v�s���ă��[�}�鍑�̃s�U��K�ꂽ�t���[�h���b�`�U���c��ɂ܂łƂǂ낫�t�B�{�i�b�`�Ƃ̌��J�������Â���܂����B�����ɏo�肳�ꂽ���̈�͎��Ɏ������ł��B
�u�����ɂT�������Ă��A��������T�������Ă����S�����ƂȂ鐔��������v
�������A���̂悤�Ȑ��͕����ŁA�����ł͂���܂���B�܂��A�t�B�{�i�b�`�͂P���������܂������A���ɂ����肻���ł��B
�����o�T�F�u���w�Z���X�v�R���f�B���X�L�[�@���@��ؕq���@��@�i�ۑP������Ёj��
�m�n�P�uH7K�v
1/11: 17��11�� ��M �X�V2/1
�m�n�Q�ukiyo�v�@�@ 1/11: 20��48�� ��M �X�V2/1
�m�n�R�u�����v�@�@ 1/11: 22��49�� ��M �X�V2/1
�����̗���F�m�n�P����m�n�R�܂ł͉m�n�P�ɍڂ��Ă���܂���
�m�n�S�u����K��v 1/11: 23��41�� ��M �X�V2/1
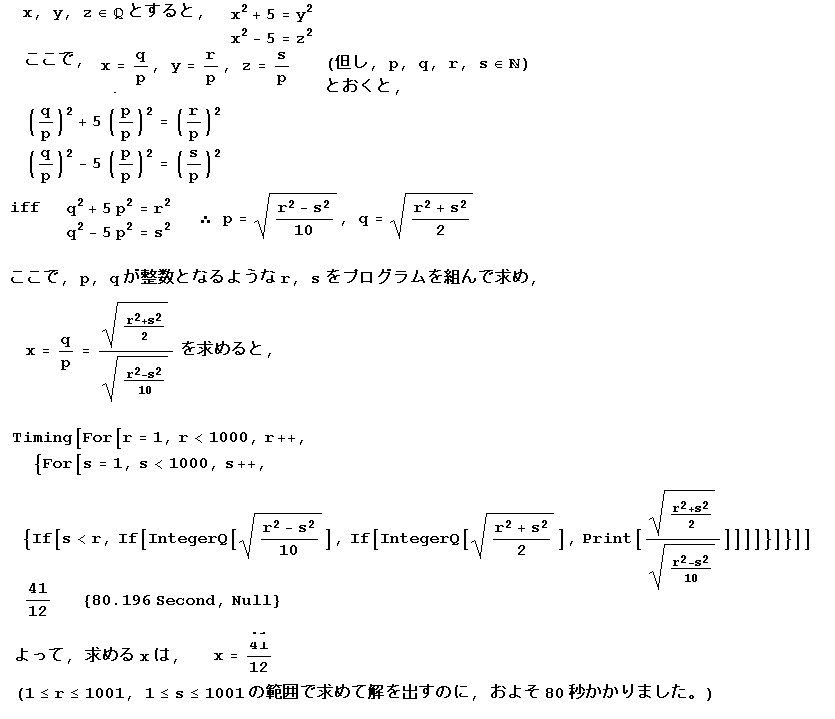 �m�n�T�utoru�v�@�@ 1/15: 11��03�� ��M �X�V2/1
�m�n�T�utoru�v�@�@ 1/15: 11��03�� ��M �X�V2/1
�����b�ɂȂ��Ă���܂��B�u�t�B�{�i�b�`���v�̉i�炵�����́H�j�𑗂�܂��B
�@���߂镪����p/q(p,q�݂͌��ɑf�Ȑ�����)�Ƃ���ƁA��ӂ̏�����
p^2-5q^2=m^2, p^2+5q^2=n^2 (m,n�͐�����)�ƂȂ�B���ꂩ��
p^2=(m^2+n^2)/2�Aq^2=(n^2-m^2)/10
�@m�An�͂Ƃ��Ɋ�ƂȂ�A�܂�(n^2-m^2)��10�Ŋ��肫���B
�@�����̏�������(m,n)��p+q=��(m^2+n^2)/2�@�{��(n^2-m^2)/10���A�G�N�Z���Ōv�Z���Ă݂܂�����A
m=31,n=49�̎�p+q=53�Ɛ����ɂȂ��āA���ꂩ��p=12,q=41������ƈ�����������邱�Ƃ��ł��܂���
41/12 ----����
���̌�A�C���^�[�l�b�g�łς�ς�ƕʂ̃T�C�g�����Ă���ƁA�ȉ~�Ȑ��̗L���_�����������ɂȂ�Ƃ��A�����������Ƃ��Ƃ��A
�łĂ��܂������A���Ԃ��Ƃꂽ��A�ȉ~�Ȑ��_�̓��发�ł������Ă��āA�ǂ݂����Ǝv���܂����A���̂��ƂɂȂ�ł��傤�B
�m�n�U�ukasama�v 1/15: 18��24�� ��M �X�V2/1
�x���Ȃ�܂������C�V�N�����܂��Ă��߂łƂ��������܂��B���N���ǂ�����낵�����肢�������܂��B
�����y���������o�肵�Ē������肪�Ƃ��������܂��B
�@����͐����_�̖��ł��ˁB���S�����Ɋւ���g�s�b�N�͐̂���悭��������Ă���ƕ����܂����A���������g�ނƂȂ�ƌ��\������̂ł��ˁB�@�������S�ɉ����ł��Ă��܂��A�r���o�߂����v���܂��B
�@�t�B�{�i�b�`�͖��̐����P�������悤�ł����A���݂͌v�Z�@������܂�����A�]���̑傫�Ȑ����łȂ�����N�ł����ȒP�Ɍ����邱�Ƃ��ł��܂��ˁB�����A�ȒP�ȃv���O�����ňȉ��̗L�������݂��邱�Ƃ��ł��܂����B
�@41/12
�@3344161/1494696
�@���ɁA���w�I�ɍl���Ă݂��̂ł����A�ȉ��̓_����������ɂ͎����Ă���܂���B
�@���t�B�{�i�b�`���͖����ɂ���̂��ǂ���
�����I�ɂ́A��L�̂Q�����̂悤�ȋC�����܂����A���炩�̍����Ɉ˂���̂ł͂���܂���̂ŁA���������������Ă݂܂��̂Ŏ��Ԃ��������B�ł́A�i�W������܂����炨�m�点�v���܂��B
������ӂ̐���u�Ƃ��܂��ƁA�����ɂT�������Ă��A��������T�������Ă����S�����ƂȂ�킯�ł�����A
�@u2 - 5 = v2�@���(1)
�@u2 + 5 = w2�@���(2)
�ƂȂ�悤�ȁA�L����v�Aw�����݂��܂��B(1)�A(2)���u����������ƁA
�@(w - v)*(w + v) = 10�@�ƂȂ�܂��B
�@w - v = a�@�@w + v = b�@�Ƃ����ƁAb = 10/a�ł�����
�@v = (10 - a2)/2a�@���(3)
�@w = (10 + a2)/2a�@���(4)
(1)����(3)���������āAv���������āAu�ɂ��ĉ�����
�@u2 - 5 =
{(10 - a2)/2a}2
�@�� u = ��(100 + a4)/2a
�����ŁAu�͊��S�����ł�����A100 + a4�����S�����łȂ���Ȃ�Ȃ����ƂɂȂ�܂��B�����āA���̂悤��u�����߂�Ηǂ��̂ł����A���w�I�ɋ��߂���@���ł��Ă��炸�A��ӂ������������ɑ��݂���̂��ǂ������킩���Ă���܂���B
�Ƃ肠�����APARI/GP�̊ȒP�ȃv���O�����ŁA�͂܂����ɂ��܂����B
�y���ʁz
1681/144 �� 41/12
11183412793921/2234116132416 �� 3344161/1494696
�y�v���O�����z
f(n)=
{
local(i,j,a,g,u);
for (j=1,n,
for (i=1,n,
if (gcd(i,j) == 1,
a = j/i;
g = 100 + a^4;
if (issquare(g),
u2 = g/(2*a)^2;
print(u2)
)
)
)
)
}
�m�n�V�u�����v�@�@ 1/15: 22��57�� ��M �X�V2/1
�������̕�����x�����߂���Ƃ��āA���������܂����B�@�܂��A�ȉ��̖���̏ؖ���lj����܂����B
�u����n�ɑ��āA(x_n,y_n)=��(n(5,25))�Ƃ���Bn����Ȃ�́A(x_n)^2�}5�͕�������5�{�ł���B
�܂��An��(0�łȂ�)�����Ȃ�́A(x_n)^2�}5�͕������ł���B�v
---------------------------------------------------
��P�R�Q�w�I�ȉ�����(��)
---------------------------------------------------
���߂�L������x�Ƃ���B
��ӂ��A����L����u,v�ɑ��āA
x^2+5=u^2 ------- (1)
x^2-5=v^2 ------- (2)
��B
(1),(2)���A
x^4-25=(x^2+5)(x^2-5)=(uv)^2
��By=uv�Ƃ���ƁA(x,y)�́A�ȉ~�Ȑ�
C: y^2=x^4-25 ------- (3)
�̗L���_�ł���B
�Ȑ�C�͑o�L���ϊ���:(x,y)��(X,Y)
X={-50}/{y-x^2}, ------ (4)
Y={-100x}/{y-x^2} ----- (5)
[�t�ϊ���:(X,Y)��(x,y)�́A
x=Y/{2X}, ------------- (6)
y={-200X+Y^2}/{4X^2} ---- (7)
�ł���B]�ɂ���āA�ȉ~�Ȑ�
E: Y^2=X^3+100X ----- (8)
��Q-���^�ł���B
����āA�ȉ~�Ȑ�E�̗L���_(X,Y)�����߂�Ηǂ��B
E�̂˂���_�Q�́AZ/2Z={(0,0), O}�ł���B�������AO�͖������_�Ƃ���B
2-descent�ɂ��AE�̗L���_�Q��rank��1�ł���A���̐�������(5,25)�ł��邱�Ƃ�������B
�܂�A
E(Q)=Z�~(Z/2Z)
={ n(5,25) : n \in Z }��{ n(5,25)+(0,0) : n \in Z
}�@�ł���B
�ȒP�Ȍv�Z�ŁAE(Q)��O�������C�ӂ̓_(X,Y)�ɑ��āA
2(X,Y)=({X^4-200X^2+10000}/{4Y^2},{X^6+500X-50000X^2+1000000}/{8Y^3}),�@-----
(9)
(X,Y)+(0,0)=({100}/{X},{-100Y}/{X^2}),�@ ----- (10)
(X,Y)+(5,25)=({5(X^2+25X+100-10Y)}/{(X-5)^2},{25(X^3+15X^2+300X+500-7XY-65Y)}/{(X-5)^3})�@----
(11)
�ł��邱�Ƃ�������B
E(Q)�̌�(X,Y)���������v�Z����B
n
n(5,25)
n(5,25)+(0,0)
-- -------------------------------------
-------------------------------
0
O
(0,0)
1 (5,
25)
(20, -100)
2 (9/4,
-123/8)
(400/9, 8200/27)
3 (25205/121,
-4006175/1331)
(2420/5041, 2482700/357911)
4 (2307361/242064, 5079780559/119095488)
(24206400/2307361,-164532721200/3504881359)
.....
C(Q)�̌�(x,y)=��(X,Y)���������v�Z����B�������A��^+,��^-�͋Ȑ�C�̖������_�Ƃ���B
n
��(n(5,25))
��((5,25)+(0,0))
-- -------------------------------------
------------------------------
0
��^+
��^-
1 (5/2,
-15/4)
(5/2, 15/4)
2 (-41/12,
-1519/144)
(41/12, 1519/144)
3 (-11285/1562,
126765585/2439844) (11285/1562,
-126765585/2439844)
4 (3344161/1494696, -535583225279/2234116132416)
(-3344161/1494696,535583225279/2234116132416)
.....
�ȒP�Ȍv�Z�ŁA(x,y)=��(X,Y)�̂Ƃ��A
��((X,Y)+(0,0))=(-x,-y),
��(-(X,Y))=(-x,y)�@�ł��邱�Ƃ�������B
����n(�������An!=0)�ɑ��āA�L����x_n,y_n,X_n,Y_n��
(X_n,Y_n)=n(5,25),
(E(Q)���n�{�_)
(x_n,y_n)=��(X_n,Y_n)�@�Œ�`����B
�������AC(Q)�̌�(x,y)��蓾��ꂽ�L����x���S��(1),(2)�����킯�ł͂Ȃ��B
�Ⴆ�Ax=�}41/12, �}3344161/1494696�̂Ƃ��Ax^2�}5�͕������ɂȂ邪�A
x=�}5/2, �}11285/1562�̂Ƃ��Ax^2�}5�͕�������5�{�ɂȂ�B
��ʂɁAn����Ȃ�́A(x_n)^2�}5�͕�������5�{�ł���̂ŁAx=x_n��(1),(2)
�����Ȃ��B�܂��An��(0�łȂ�)�����Ȃ�́A(x_n)^2�}5�͕������ł���̂ŁA�@x=x_n��(1),(2)�������Ƃ�������B
[�ؖ�]
���ŏ��ɁA"(x_n)^2�}5�������� <====> X_n��������"�������B
�@�@�ȒP�̂��߂ɁAn���ȗ�����B(x,y)=��(X,Y)�Ƃ���ƁA(6),(7),(8)���A
x^2�}5=(Y/(2X))^2�}5=(Y^2�}20X^2)/(4X^2)=(X^3+100X�}20X)/(4X^2)
=X(X�}10)^2/(4X^2)=X({X�}10}/{2X})^2
X�͗L�����Ȃ̂ŁAx^2�}5���������ł���̂́AX���������ł���Ƃ��ł���A�@���̂Ƃ��Ɍ���B
�����ɁAn��0�ȊO�̐����̂Ƃ��AX_{2n}�͕������ł��邱�Ƃ������B
(9)�����(X_{2n},Y_{2n})=2(X_n,Y_n)���A
X_{2n}={(X_n^2-100)^2}/{4Y_n^2}=({X_n-100}/{2Y_n})^2�@ ����āAX_{2n}�͕������ł���B
���Ō�ɁAn�������̂Ƃ��AX_{2n+1}�͕�������5�{�ł��邱�Ƃ������B
�@�@n=0�̂Ƃ��́AX_1=5���A���炩�B
�@�@n!=0�̂Ƃ��́A
(11)�����(X_{2n+1}+Y_{2n+1})=(X_{2n},Y_{2n})+(5,25)���A
�@�@�@�@X_{2n+1}={5(X_{2n}^2+25X_{2n}+100-10Y_{2n])}/{(X_{2n}-5)^2}
={5(X_{2n}^3+25X_{2n}^2+100X_{2n}-10X_{2n}Y_{2n])}/{X_{2n}(X_{2n}-5)^2}
={5(Y_{2n}^2+25X_{2n}^2-10X_{2n}Y_{2n])}/{X_{2n}(X_{2n}-5)^2}
={5(Y_{2n}-5X_{2n})^2}/{X_{2n}(X_{2n}-5)^2}
=(5/X_{2n})*({Y_{2n}-5X_{2n}}/{X_{2n}-5})^2
X_{2n}�͗L�����̕������AY_{2n}�͗L�����Ȃ̂ŁAX_{2n+1}�͕�������5�{�ł���B
[�ؖ��I���]
�܂��A(10)���AE(Q)�̔C�ӂ̓_(X,Y)�ɂ��āA
�@�@�@�@�@(X,Y)��X���W�������� <===>(X,Y)+(0,0)��X���W���������ł��邱�Ƃ�������B
����āA����(1),(2)�����L����x�����߂�ɂ́A����n(n!=0)�ɑ��āA
(x_n,y_n)=��(n(5,25))��x���Wx_n���v�Z����Ώ\���ł���B
�����ŁA��(n(5,25)+(0,0))=(-x_n,-y_n)�ł���̂ŁAn>0�̏ꍇ�̂v�Z����B
n=2,4,6,...�ɑ��ă�(n(5,25))��x���Wx_n�����߂�ƁA�ȉ��̂悤�ɂȂ�B
-41/12,
3344161/1494696,
-654686219104361/178761481355556,
-249850594047271558364480641/5354229862821602092291248,
160443526614433014168714029147613242401001/50016678000996026579336936742637753055940,
-209239116668342644167838867143329714389679018137228536721441/93092380947563478644577555596900542802151091304399908363272,
653152954009158143378427536560733420320797953915756014095625317096936904977985961/165212943236364556817454960196622119200395589469467839738735336681091141974929836,
3896941041458487485320832722469963686366256264486004169772710584821176712668535259971051251201565099266561/167019439477564254804819333692197516475269570978824403519721702282259070147808848039273138602363503527584,
-39237885850430493626909674952750943784591172430352517285024742033896533808220451105238021689439529973471632789306928489835884212163241/12952454930469561017859054695383398376216914979916496971716496296075783109382658016757987519838824348906938668524076790678410751270508,
819115590828533344363410662412264643379752066019183683929303651124586853669504387320308409413889983068897449835893620439166082535269226761968418573264897156499604001/361099956694584921325844298628071074932266255535444467758581806245113643624628862872331108319421687852576797589404506630373073554588284615643777818720192420057751880,
....
������A���L�����ł����x=|x_n|�����߂�ƁA
41/12,
3344161/1494696,
654686219104361/178761481355556,
249850594047271558364480641/5354229862821602092291248,
160443526614433014168714029147613242401001/50016678000996026579336936742637753055940,
209239116668342644167838867143329714389679018137228536721441/93092380947563478644577555596900542802151091304399908363272,
653152954009158143378427536560733420320797953915756014095625317096936904977985961/165212943236364556817454960196622119200395589469467839738735336681091141974929836,
3896941041458487485320832722469963686366256264486004169772710584821176712668535259971051251201565099266561/167019439477564254804819333692197516475269570978824403519721702282259070147808848039273138602363503527584,
39237885850430493626909674952750943784591172430352517285024742033896533808220451105238021689439529973471632789306928489835884212163241/12952454930469561017859054695383398376216914979916496971716496296075783109382658016757987519838824348906938668524076790678410751270508,
819115590828533344363410662412264643379752066019183683929303651124586853669504387320308409413889983068897449835893620439166082535269226761968418573264897156499604001/361099956694584921325844298628071074932266255535444467758581806245113643624628862872331108319421687852576797589404506630373073554588284615643777818720192420057751880,
....
�ƂȂ�B����ɁA������|x_{2n}| (�������An�͐�����)�ȊO�ɂ�(1),(2)�̐�
�L������x�͂Ȃ����Ƃ�������B
���łɁA�L�����̕�����x^2�́A
1681/144,
11183412793921/2234116132416,
428614045485163378013009218321/31955667216432795403292069136,
62425319345774489875576913540908007654663493663770881/28667777423930631959129990083752908396266457397504,
25742125232476274945600804344670821085186747239792972834270694018194679471285802001/2501668078255319881397266106072508369628265230233648767096664663655320808769283600,
43781007944148304548244210396281989964103136439445456775192309124306675701466399112933759276955808140583881001229116481/8666191390486279754082343551208369565243342312911502069880314222532921884497792974334497667304622471072390889918545984,
426608781330889452801634842349311903911234872598242992095908202911520460074823221702666116328171946744340015074718237397239762331073242631060353386066027913093521/27295316612822217161273099207575492045965455960163391163605190041343587975559930961845574372758947682450233333730822269136896257920943624483822742853937122986896,
15186149480603561077873486951173749559525479302211996827405127217678870732032108537181044477898873408310514497391618637431614257333642103164013127658012672837118280294149649202051220990692972277960589780132766721/27895493163399749075975576686531661804502467274390286244455076465675913453039254381581795143230099427207818140220697782396804741139066893940555963636702931247304221072896856752708889710376859209702011848877056,
1539611686011413542083853952876101197813720598928842362281142122759999414139721553168823583530573400260628057642251722956499411322456242317077763749152723454622785137872066217490415494927685153231297369778666247288095457938486721045156630353438379089460093328831624081/167766088725845240741629149618209524558953232824585954175859084429812231591512275744978565038525417963266067181939823910059627946958305306445772534813068796160387217063376062654475164246390564601247792814781346570898903010493898213658424521601656058055071936190578064,
670950351138377259092284101030243992075735187961753049569437576149342919163534134400715328304041011837130473979926268744958367991476835308684797605148274351463092401046820105830147087240950183114781656537205018150428604021899028891442218330614015805991732344436245975625469537413578241893861017592120388948596840231846469815208001/130393178724831105540499888728123964993760914585113543805532300725628752816193378723210058935003671538698505176647864287100113923212470726672664068391983522571009534051653751290362266567203731273645568902122686257417548425629372093443265825101539026315379232291183634502413110016687819238877658951167400492237012436834479643534400,
....
�ł���B
�m�n�W�ukasama�v 1/20: 20��03�� ��M �X�V2/1
�y���j�z��ӂ̊��S�������̎Z�o��x�Ax+n�Ax-n�����ׂėL�����̕������@�ˍ�����n�Ɋւ���ȉ~�Ȑ���̗L���_�̎Z�o
�ƍl���āA�ȉ~�Ȑ���̗L���_���v�Z���邱�ƂŁA�t�B�{�i�b�`�����Z�o���܂��B
�y�z
�@������n�Ƒȉ~�Ȑ�y2 = x3 - n2x��̗L���_�̊W�@n���������i���j�Ƃ���ƁA�K���ȗL����a�Ab�Ac>0�����݂��āA
�@a2 + b2 = c2�@n = ab/2�@�ł��B�����ŁA
�@x = c2/4�@�Ƃ����ƁA�@x + n = (a+b)2/4�@x
- n = (a-b)2/4�@�ł�����A
x�Ax+n�Ax-n���S�ėL�����̕�������x(x+n)(x-n)�͗L�����̕������ł��B
���̂��Ƃ́A�ȉ~�Ȑ�En�@�@y2 = x(x+n)(x-n)�@�ˁ@y2
= x3 - n2x�@�������łȂ�(y��0�Ȃ�)�L���_(x,y)�������ƂƓ��l�ł��B
����������̏ꍇ�A�������Ƃ͂R�ӂ��L�����ƂȂ�悤���p�O�p�`�̖ʐςƒ�`����Ă��܂����A��L�̑ȉ~�Ȑ�En�����悤��n�ƒ�`���Ă��邱�Ƃ�����悤�ł��B
�A�T�͍�����
H.Nakao's Elliptic Curves
Topics(http://www.kaynet.or/~kay/misc/index.html)�ɂ��ƁA�T�͍������ŁA�ȉ~�Ȑ�En�̗L���_�Q�̈ʐ���rank
En(Q)=1�ŁAEn(Q)/tor(En(Q))�̐�����=[-4
: -6 : 1]�ł���悤�ł��B
2004/01/20�NjL�F���ۂɁAmwrank2.8(John Cremona���쐬�̃v���O����)�삳���Ē��ׂĂ݂����ʂ�⑫�P�ɋL�ڂ��܂��B
�B�t�B�{�i�b�`�����Z�o
�T���������Ȃ̂ŁA�ȉ~�Ȑ�y2 = x3 - 52x��̗L���_���v�Z���邱�ƂŁA�t�B�{�i�b�`�����Z�o���邱�Ƃ��ł��܂��Bpari/gp�ŊȒP�ȃv���O�����i�⑫�Q�Q�Ɓj�Ōv�Z���܂����B�v���O�����̓��e�́A������[-4, -6]����L���_(x,y)���v�Z���āA
�@a = |(52 - x2)/y|�@�@b = |2nx/y|�@�@c = |(52 + x2)/y|
�̗L����a�Ab�Ac�����߁A�@��x = �}c/2�@�@���Z�o���܂��B
�m���s���ʁn
(00:13) gp > read("���w/���̗���/��132��/dai132.gp")
(00:13) gp > dai132(5,ellinit([0, 0, 0, -25,
0]),[-4, -6],15)
41/12
-41/12
-3344161/1494696
3344161/1494696
654686219104361/178761481355556
-654686219104361/178761481355556
249850594047271558364480641/5354229862821602092291248
-249850594047271558364480641/5354229862821602092291248
����ȉ��A���͂������Ȃ�̂ŏȗ����
�y�⑫�P����ȉ~�Ȑ�En�̗L���_�Q�̈ʐ��Ɛ������z�@�Q�l�܂łɁA���샍�O���L�ڂ��܂��B
[kasama@KEN tmp]$ mwrank
Program mwrank: uses 2-descent (via 2-isogeny if
possible) to
����������
using base arithmetic option LiDIA_INTS (LiDIA bigints, no multiprecision floating point)
Enter curve: [0, 0, 0, -25, 0] �� �ȉ~�Ȑ�En�̎w��
Curve [0,0,0,-25,0] :
����������
-------------------------------------------------------
Computing full set of 2 coset representatives for
2E(Q) in E(Q) (modulo torsion), and sorting into height order....done.
Rank = 1 �� �ʐ�
After descent, rank of points found is 1
Generator 1 is [-4 : 6 : 1]; height 1.8994821725318 �� �������ƍ���
The rank has been determined unconditionally.
The basis given is for a subgroup of full rank of the Mordell-Weil
group
(modulo torsion), possibly of index greater than 1.
Regulator (of this subgroup) = 1.8994821725318
(0.4 seconds)
�y�⑫�Q����v���O����(dai132.gp)�z
�Q�l�܂łɁA�v���O�������L�ڂ��܂��B
dai132(n, e, ptE, num)=
{local(i);�@ for (i = 1, num,�@printPoint(n, ellpow(e, ptE, i));�@ printPoint(n, ellpow(e, ptE, -i)) );}
printPoint(n, pt)={ local(x, y, c);�@ x = pt[1]; y =
pt[2];�@ c = (n^2 + x^2) / y;�@print(c/2);�@}
�m�n�X�ukiyo�v�@�@ 1/21: 01��09�� ��M �X�V2/1
�����́B�ikiyo�j�ł��B���������b�ɂȂ��Ă��܂��B
�����I���@�łQ�ڂ������܂����B
(3344161/1494696)^2+5=(4728001/1494696)^2=22353993456001/2234116132416
(3344161/1494696)^2-5=(113279/1494696)^2=12832131841/2234116132416
�m�n10�u�X���v�@�@ 1/22: 21��58�� ��M �X�V2/1
�S�P/12�ł��B�@�i�S�P/�P�Q)^�|�T���i�R�P/�P�Q)^�@�i�S�P/�P�Q)^�{�T���i�S�X/�P�Q�j�O�@�O�͂Q��̈Ӗ��ł��B
�m�n11�u�O�p��K�v 1/25: 00��29�� ��M �X�V2/1
���R�����g����132��i�t�B�{�i�b�`���j����܂��B
�u���L�v��q�����Ă���܂��ƁA�F����u�ȉ~�Ȑ���̗L���_�v�Ƃ���������Ă��܂����A���ɂ� ?? �Ȃ̂ŁA���͎����ɂł���l�����ʼn����܂����B
���̉����̂��̂�10���قǑO�ɂł��Ă����̂ł����A�Ӓn�ł������P��{�����ƃ��L�ɂȂ��Ă���܂����B
�G�N�Z���ő{�����̂ł����A�ꎞ��(���̉��Łj�T���� p �������������Ǝv�����̂ł����A11����
p^2 ���G�N�Z���̓����� Sqrt() �ŊJ���ۂ̌덷�i�P�̈ʂ̂P�j�ŁA���ɏI����Ă��܂��܂����B����A�̕��X�̉�����w���Ă��������܂�

�����̗���F�m�n�S����m�n�P�P�܂ł͉m�n�Q�ɍڂ������Ē����܂���
�@�@�@�@������@�@mizuryu@aqua.ocn.ne.jp
![]()
