平成17年1月23日
 [流れ星]
[流れ星]
第149回数学的な応募問題解答NO2
<解答募集期間:1月3日〜1月23日>
[外接する3円]
最近、中央新書から出版された秋山仁著の「知性の織りなす数学美」という本を読んでいます。その中に、
江戸時代の和算家『関孝和』のこぼれ話が出ていました。次の問題が出ていて、生徒と一緒に解き始めましたが、
未だに解けていません。では、その問題です。
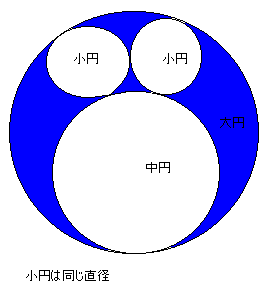
図の青の部分の面積が120、中円と小円の直径の差が5であるとき、大、中、小の3種類の直径を求めよ。
だだし、中円と小円は互いに外接、中円と大円は内接、2つの小円と大円は内接している。
【追記】1月3日の夜記入
実は、問題文は「知性の織りなす数学美」にある通りですが、生徒と考えていたとき気がついたのですが、図の青の部分の面積が120は誤記のような気がします。そこで、面積を120π(πは円周率)としても考えてください。
さらに、類題として、図の通りの4つの円で、大円、中円、小円の半径をそれぞれ、R,r ,t としたとき、tをR,rで表してください。(この類題が和算の本にあるものです)
NO11「浜田明巳」01/12:17時10分受信 更新1/23
類題の解答
xy座標を導入する.大円の中心を原点O1(0,0),中円の中心をO2(0,−R+r),右側の小円の中心をO3とし,左右の小円がy軸で接しているとする.
O1O3とx軸の正の向きとなす角をθ(0<θ<π/2)とすると,
O3((R−t)cosθ,(R−t)sinθ)
またO3のx座標はtであるから,
(R−t)cosθ=t
R−t>0から,cosθ=t/(R−t)
0<θ<π/2から,sinθ>0
∴sinθ=(1−cos2θ)1/2=[1−{t/(R−t)}2]1/2={(R−t)2−t2}1/2/(R−t)(∵R−t>0)
∴sinθ=(R2−2Rt)1/2/(R−t)
故にO3のy座標は,
(R−t)sinθ=(R−t)・(R2−2Rt)1/2/(R−t)=(R2−2Rt)1/2
∴O3(t,(R2−2Rt)1/2)
∴O2O32=(t−0)2+{(R2−2Rt)1/2−(−R+r)}2=t2+(R2−2Rt)−2(R2−2Rt)1/2(−R+r)+(−R+r)2
∴O2O32=t2+2R2−2Rt+2(R2−2Rt)1/2(R−r)−2Rr+r2………(1)
またO2O3=r+tであるから,
O2O32=(r+t)2=r2+2rt+t2………(2)
(1),(2)から,
t2+2R2−2Rt+2(R2−2Rt)1/2(R−r)−2Rr+r2=r2+2rt+t2
∴2R2−2Rt+2(R2−2Rt)1/2(R−r)−2Rr=2rt
∴R2−Rt+(R2−2Rt)1/2(R−r)−Rr=rt
∴(R2−2Rt)1/2(R−r)=(R+r)t−R(R−r)
故にこの式は,次の2つと同値である.
(R2−2Rt)(R−r)2=(R+r)2t2−2R(R+r)(R−r)t+R2(R−r)2………(3)
かつ (R+r)t−R(R−r)≧0………(4)
(3)から,
R2(R−r)2−2R(R−r)2t=(R+r)2t2−2R(R2−r2)t+R2(R−r)2
∴−2R(R−r)2t=(R+r)2t2−2R(R2−r2)t
∴(R+r)2t2=2R(R2−r2)t−2R(R−r)2t=2R(2Rr−2r2)t=4Rr(R−r)t
R+r>0,t>0から,
t=4Rr(R−r)/(R+r)2………(答)
問題の解答
上記の結果から,
t=4Rr(R−r)/(R+r)2………(5)
(R+r)t−R(R−r)≧0………(4)
問題の条件から,
2r−2t=5………(6)
π(R2−r2−2t2)=120π………(7)
(6)から,r=5/2+t………(6)'
(7)から,R2=r2+2t2+120………(7)'
この連立方程式(5),(4),(6)',(7)'を次のVBSRIPTで解く.
option explicit
dim S
dim dankai1
dim dankai2
dim Rr
dim r2
dim t
dim t_min
dim t_max
dim kotae_Rr
dim kotae_r2
dim kotae_t
dim kizami
dim sa
dim min
for dankai1=1 to 2
if dankai1=1 then
S=120
else
S=120*pi
end if
for dankai2=1 to 14
if dankai2=1 then
t_min=1
t_max=20
kizami=.1
min=1000000
else
t_min=kotae_t-kizami
t_max=kotae_t+kizami
kizami=kizami*.1
end if
for t=t_min to t_max step kizami
r2=2.5+t
Rr=sqr(r2*r2+2*t*t+S/pi)
if (Rr+r2)*t-Rr*(Rr-r2)>=0 then
sa=abs(t-4*Rr*r2*(Rr-r2)/(Rr+r2)/(Rr+r2))
if min>sa then
min=sa
kotae_Rr=Rr
kotae_r2=r2
kotae_t=t
end if
end if
next
next
if dankai1=2 then
S="120π"
end if
document.write("S="&S&"のとき,大円の直径="&(kotae_Rr*2)&",
中円の直径="&(kotae_r2*2)&", 小円の直径="&(kotae_t*2)&",
誤差="&min&"< br>")
next
function pi()
pi=4*atn(1)
end function
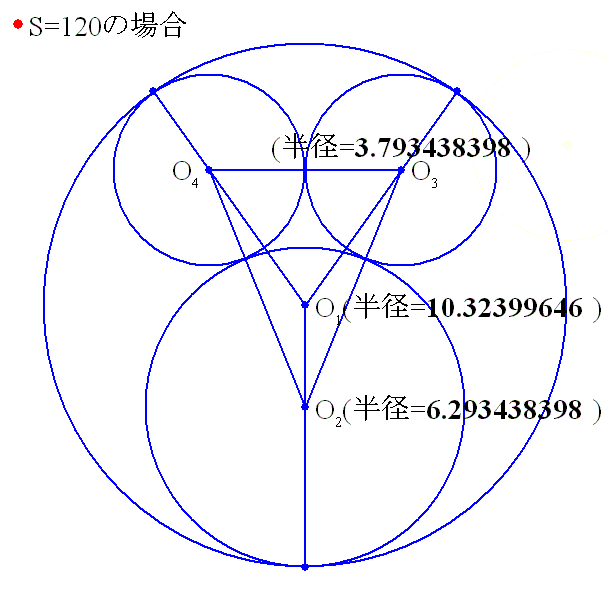
S=120のとき,大円の直径=20.6479929272978, 中円の直径=12.586876796801, 小円の直径=7.586876796801,
誤差=1.77635683940025E-15
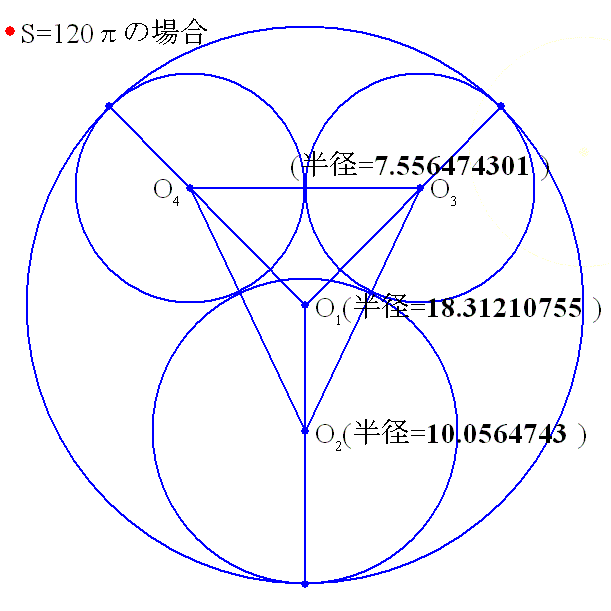
S=120πのとき,大円の直径=36.6242151082522, 中円の直径=20.1129486013588, 小円の直径=15.1129486013588,
誤差=1.77635683940025E-15
NO12「三角定規」01/12: 22時00分受信 更新1/23

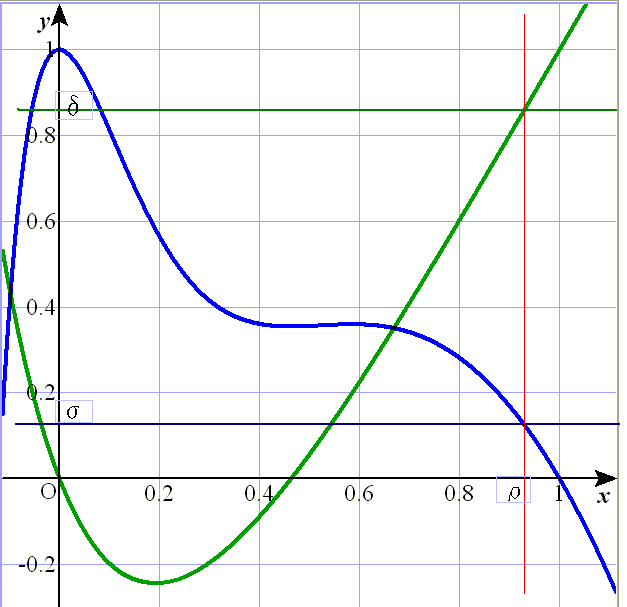
ところで,添付の一太郎文書に分数関数のグラフを貼り付けましたところ,サイズが3Mを超え,1回で送信できなくなりました。
そこでグラフのみ別送しますので,お手数ですが,そちらで文書右下の空所に縮小して貼り付けてくださいませんでしょうか。
その際,文書中に残っている2つの数式をグラフ上適所に置いてください。
y=1−x^2−… が青線,y=x(1−… が緑線です。
よろしくお願いします。
<水の流れ: そうしてあげたいのですが、ちょっと トラブって いまして、今回はお許しください。>
NO13「kashiwagi」01/14:18時36分受信
更新1/23
本当ですね。面積の関係式から値を出して、それに代入し合っているという基本 的な間違いを犯しておりました。早速Excel計算を致しました。
R=18.30、r=10.05、t=7.55となりました。
うーんー、コンピュータの偉大さを垣間見させて頂きました。宜しくお願い申し上げ ます。
NO14「kiyo」
01/18:04時09分受信 更新1/23
いつもお世話になっています。清川(kiyoI)です。
今後とも宜しくお願いします。
REM へロンの公式による。120πとする。
REM 16*X^6-144*X^5+1152*X^4-7780*X^3+33680*X^2-35850*X-23225=0 Xは小円の半
径。
LET X=2.214915159043
LET Y=SQR(12*X^2+20*X+505)/2-2*X
PRINT "面積";(2*X+Y)^2-2*X^2-(X+2.5)^2;"π"
PRINT "小円の直径";2*X
PRINT "中円の直径";2*X+5
PRINT "大円の直径";2*(2*X+Y)
出力
面積 120 π
小円の直径 4.429830318086
中円の直径 9.429830318086
大円の直径 24.6610724244093
<水の流れ:この値ではなさそうです>
No15「中川幸一」
01/23:23時34分受信 更新1/25
![]()
