�����P�V�N�T���P�T��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��P�T�S�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�S���P�V���`�T���P�V��
�m�s�b�N�̌����n
�F����A���p�`�̖ʐς����߂�f���炵���������Љ�܂��B�����ł́A�菇�ɂ��������āA�ؖ����Ă����܂��B
|
�����F���ׂĂ̒��_���i�q�_�ɂ��鑽�p�`���A�����ɂ��̊i�q�_�������A����ɂ��̊i�q�_�����Ƃ��A���̖ʐς� |
�菇�P�F�i�q�̐���ɂS�ӂ����钷���`�̂Ƃ��A�s�b�N�̌������ؖ�����B
�菇�Q�F�i�q�̐���ɒ��p���͂��ނQ�ӂ����钼�p�O�p�`�̂Ƃ��A�s�b�N�̌������ؖ�����B
�菇�R�F���p�`�`���Q�̑��p�`�a�C�b�ɕ��������Ƃ��i���̂P�j
�@�@�@�@�@���p�`�a�C�b�ɑ��ăs�b�N�̌��������藧�Ȃ�`�ɑ��Ă����藧���Ƃ��ؖ�����B
�菇�S�F���p�`�`���Q�̑��p�`�a�C�b�ɕ��������Ƃ��i���̂P�j
�@�@�@�@�@���p�`�`�C�a�ɑ��ăs�b�N�̌��������藧�Ȃ�b�ɑ��Ă����藧���Ƃ��ؖ�����B
�菇�T�F�i�q�_��ɒ��_������ʂ̎O�p�`�̂Ƃ��A�O�p�`�̒��_��ʂ�A�S�ӂ��i�q����ɂ���}�̂悤�Ȓ����`���l����B
�@�@�@�@�@���̐}�𗘗p���āA�s�b�N�̌������ؖ�����B�i���͕\���ɂȂ�j
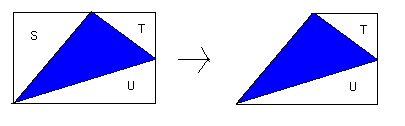
�_���U�F�i�q�_������łł����ʂ̑��p�`�̂Ƃ��A�s�b�N�̌������ؖ�����B�i���͕\���ɂȂ�j
�����̏o�T�F������ѐ��w�R�[�X�u���w�T�����̂��ށv�u��_�@��g���X��
�m�n�P �ucbc�v�@�@ 4/20: 22��37����M �X�V5/15

�m�n�Q�uToru�v 4/21:
14��41����M �X�V5/15
��P�T�S��@�s�b�N�̒藝�̉𑗂�܂��B
�ƂĂ��������ؖ��Ō��ʂ��������A�m���ɂ��炵���藝���Ǝv���܂��B�菇�Q���菇�R�A�S�̌��ɂ����Ă���A���̌��ʂ��g����̂ŁA
�X�ɂ�������Ƃ����ؖ��ɂȂ邩�Ƃ��v���܂������A�菇�R���l����\�s���K�Ƃ��Ď菇�Q������Ƃ���A
���҂ɔz�������e�ȏo��Ȃ̂��ȂƎv�������܂����B�@
�菇�P�@�����`�̕ӂ̒������@x,y �Ƃ���Ɓ@a=(x-1)(y-1),�@b=2(x+y)
a+(b/2)-1=xy �ƂȂ��Ă��̎��A�����͂Ȃ肽�B
�菇�Q�@���p�����ނQ�ӂ�x,y�@�Εӏ�i�[���܂܂��j�̊i�q�_�̐������Ƃ����
a=�i(x-1)(y-1)-���j�^2, �@b=x+y+1+���@
a+(b/2)-1=xy/2 �ƂȂ��Ă��̎��������͐��藧�B
�菇�R�@���p�`A�̓����̊i�q�_�̐�a(A), ����̊i�q�_�̐�b(A)�ȂǂƂ���킷�B
�@B�AC�̋��ʕ�����A�̓����ɂȂ�i�q�_�i���Ȃ킿��������̓_��A�����ɂȂ�_�j�̐������Ƃ���
a(A)=a(B)+a(C)+��, b(A)= b(B)+b(C)-2��-2���
a(A)+(b(A)/2)-1= a(B)+(b(B)/2)-1+ a(C)+(b(C)/2)-1 �ƂȂ���B�AC�Ő��藧�Ă�A
�ł������͐��藧�B
�菇�S�@�菇�R�Ɠ����L����p���āA
a(C)+(b(C)/2)-1=a(A)+(b(A)/2)-1-( a(B)+(b(B)/2)-1) ��� A,B�Ő��藧�Ă�C��
�������͐��藧�B
�菇�T�@�菇�P��蒷���`�ł͌��������藧���A�菇�Q���S,T,U���ꂼ��ł����������藧����A�菇�S��蒷���`����AS,T,U�̕��������ɏ����ƍl����A�C�ӂ̊i�q�O�p�`�Ō����͐��藧�B
�菇�U�@��ʂ̑��p�`�́A�L���̎O�p�`�ɕ����ł���̂ŁA�菇�T����ю菇�R������Ԃ��p����A���̎��������͐��藧�B
�m�n�R�ukashiwagi�v4/22: 08��28����M
�X�V5/15
�����b�ɂȂ�܂��B����̖��͖{���ɋ����[���A�Y��ȊW�ł��ˁB���߂Ēm��܂����B
���㉽���Ɏg�������ł��ˁB�������A�ؖ��̎菇�����ɓK���Ă���A�{���Ɉ���X�[������ ����A�y���݂Ȃ���菇�U�܂ŒH�蒅���A��ʂ̑��p�`�ł̏ؖ��������v���܂����B�̂͘_�� �I�ؖ��͖ь������Ă����̂ł����A���̔N�ɂȂ萔�w�̘_�̔������Ɋ����������܂����B
154���
�菇�P�D
�@����M�A�c��N�̊i�q�_���������`VWXY���l����B����Ƃ��̖ʐ�A�́AA=�iM-1�j�iN-1�j�ł���B
�Ƃ���ŊO���̊i�q�_��b���Q�iM+N�j-�S���Q�iM+N-2�j�A�����̊i�q�_��a��MN�|�Q�iM+N-2�j�ł���B������a�{�ib/2�j-1���v�Z����ƁA
MN�|�Q�iM+N-2�j+�iM+N-2�j-1=�iM-1�j�iN-1�j=A
�����ăs�b�N�̌������ؖ����ꂽ�B
�菇�Q�D
�@��L�����`�̒��_Y���ЂƂ��iX�����j�̊i�q�_Z��U,Y�̎O�_���Ȃ钼�p�O�p�`���l����ƁA���̖ʐ�B�́AB���iM-1�j/2
�ł���B
���̒��p�O�p�`�̊O���̊i�q�_��b��M+1,�����i�q�_��a���O�ł��邩��Aa�{�ib/2�j-1���v�Z����ƁA�iM-1�j/2��B�ƂȂ�B
�����ăs�b�N�̌������ؖ����ꂽ�B
�菇�R�D
�@��L�����`�̂����A���p�O�p�`UYZ�ȊO�̑��p�`UVXZ�̖ʐς�C�Ƃ����
C���iM-1�j�iN-1�j-�iM-1�j/2=�iM-1�j�iN-3/2�j/2�A�O���̊i�q�_��b���Q�iM+N-2�j-�iM-1�j�A
�����i�q�_��a��MN�|�Q�iM+N-2�j�ł��邩��Aa�{�ib/2�j-1���v�Z����ƁA�iM-1�j�iN-3/2�j/2��C�ƂȂ�B
�����ăs�b�N�̌������ؖ����ꂽ�B�����AB�ɂ��Ă͎菇�Q�ŏؖ�����Ă���̂�B��C�ɂ��ăs�b�N�̌��������藧�B
����A�ł��邪���łɎ菇�P�Ńs�b�N�̌��������藧���Ƃ͏ؖ�����Ă���B
������A�������B�AC�Ńs�b�N�̌��������藧�Ă�A�ł����藧���Ƃ��ؖ����ꂽ�B
�菇�S�D
�@�菇�P�C�Q��蒷���`A�ƒ��p�O�p�`B�ɂ��ăs�b�N�̌������������Ă���B�c��C�ɂ��Ă��菇�R�ŏؖ������B�����āA���X��A�Ɠ����ꂽ�Е�B�Ńs�b�N�̌�������������Γ����ꂽ�c���C�ł��s�b�N�̌������������邱�Ƃ��ؖ����ꂽ�B
�菇�T�D
�@�菇�P��肱�̒����`�ɂ��Ă̓s�b�N�̌�������������B���A�������������p�O�p�`S�ɂ��Ă��菇�Q�ɂ�萬�����Ă���B
����Ǝ菇�S���c��̑�`�ɂ��Ă���������B
�@���ɑ�`�p�O�p�`T�Ǝl�p�`�ɕ�������B�����T�ɂ��Ă͎菇�Q���s�b�N�̌�������������̂ŁA
�菇�S���l�p�`�ɂ��Ă���������B���A���̎l�p�`�p�O�p�`U�Əؖ����ׂ���ʂ̎O�p�`�ɕ�������B
U�ɂ��Ă͎菇�Q���s�b�N�̌�������������̂ŁA�菇�S���c��̈�ʂ̎O�p�`�ɂ��Ă��s�b�N�̌�������������B
�菇�U�D
�@���p�`�͕K�������̎O�p�`�ɕ��������B�����S�Ă̎O�p�`�ɂ��Ď菇�Q�y�тT���s�b�N�̌�������������B
����ƍŏ��̓�̎O�p�`�Ŏ菇�R���s�b�N�̌����������A���̐}�`�Ǝ��̎O�p�`�̂������ɂ��菇�R���s�b�N�̌�������������B
���̗l�Ɏ菇�R���J��Ԃ��K�p���Ă����Α��p�`�ɑ��s�b�N�̌�������������B�@�@�@
�m�n�S�ukasama�v�@4/28�@16��12����M�@�X�V5/15�@
����ɂ��́A(kasama)�ł��B�����y���������o�肵�Ē������肪�Ƃ��������܂��B
�i�q��ɕ`���ꂽ���p�`�̖ʐς��Y��Ȍ`�ŕ\���ł���̂ł��ˁB
���낢��ƒ��ׂĂ���ߒ��ŁA�w���_�ȊO�ɓ����ɂ��ӏ�ɂ��i�q�_�̂Ȃ��O�p�`�̖ʐς�1/2�x�Ƃ������Ƃ��킩��܂��āA�ƂĂ��s�v�c�ȋC�����܂����B
�y�菇�P�z
�����I�Ȃ����ł����A���}�̂悤�ɁA�ʐ�1�̊i�q�Ɗi�q�_�ɔԍ���t���܂��B

�ŁA���̂悤�Ɋ֘A�t�����܂��B
�@A1��P1,A2��P2,���,Aa��Pa
�@B1��Q1,B2��Q2,���,Bb/2-1��Qb/2-1
�֘A�t����ꂽ�i�q�_�̌�a+b/2-1���ʐςȂ̂ŁA�s�b�N�̌����͐������܂��B
�y�菇�Q�z
��L�̒����`�ɑΊp��(���F)���Ђ��A���p�O�p�`�����܂��B
�@�@
�����āA�����`�̓����̊i�q�_��=a�A����̊i�q�_��=b�A�Ίp����ɂ���i�q�_��=p�Ƃ��܂��B
����ƁA�菇�P��蒷���`�̖ʐ�S��
�@S=a+b/2-1
�ł��B�����ŁA���p�O�p�`�ɂ���
�@S1/2=�����̊i�q�_��+����̊i�q�_��/2-1={a-(p-2)}/2+(b/2+p-1)/2-1=a/2+b/4-1/2
�@��2�S1/2=a+b/2-1=S
�Ȃ̂ŁA��L��S1/2�͎O�p�`�̖ʐς�\���Ă��܂��B����āA�s�b�N�̌����͐������܂��B
�y�菇�R�z
�@���p�`A�AB�AC�̖ʐρA�i�q�_����
|
���p�` |
�ʐ� |
�i�q�_�� |
|
|
���� |
���� |
||
|
A |
�| |
aA |
bA |
|
B |
SB |
aB |
bB |
|
C |
SC |
aC |
bC |
�Ƃ��܂��B�������A���p�`B�AC��p�̊i�q�_�����L���Ă���Ƃ���ƁA
�@aA=aB+aC+p-2
�@bA=bB+bC-2p+2
�ł����ASA=aA+bA/2-1�ƒ�`����ƁA
�@SA=aB+aC+p-2+(bB+bC-2p+2)/2-1=(aB+bB/2+1)+(aC+bC/2+1)
�����ŁA����ɂ��A���p�`B�AC�ɂ̓s�b�N�̌����͐�������̂ŁA
�@SB=aB+bB/2-1
�@SC=aC+bC/2-1
�ł�����ASA=SB+SC�ƂȂ�ASA=aA+bA/2 -1�͑��p�`A�̖ʐς�\���Ă��邱�ƂɂȂ�܂��B
����āA�s�b�N�̌����͐������܂��B
�y�菇�S�z
�@���p�`A�AB�AC�̖ʐρA�i�q�_����
|
���p�` |
�ʐ� |
�i�q�_�� |
|
|
���� |
���� |
||
|
A |
SA |
aA |
bA |
|
B |
SB |
aB |
bB |
|
C |
�| |
aC |
bC |
�Ƃ��܂��B�������A���p�`A�AB��p�̊i�q�_�����L���Ă���Ƃ���ƁA
�@aC=aA-aB-p+2
�@bC=bA-bB+2p-2
�ł����ASC=aC+bC/2-1�ƒ�`����ƁA
�@SC=aA-aB-p+2+(bA-bB+2p-2)/2-1=(aA+bA/2+1)-(aB+bB/2+1)
�����ŁA����ɂ��A���p�`A�AB�ɂ̓s�b�N�̌����͐�������̂ŁA
�@SA=aA+bA/2-1
�@SB=aB+bB/2-1
�ł�����ASC=SA-SB�ƂȂ�ASC=aC+bC/2 -1�͑��p�`C�̖ʐς�\���Ă��邱�ƂɂȂ�܂��B
����āA�s�b�N�̌����͐������܂��B
�y�菇�T�z
�@�菇�P��蒷���`�Ƀs�b�N�̌����͐��藧���܂��B�菇�Q��蒼�p�O�p�`S�AT�AU�Ƀs�b�N�̌����͐��藧���܂��B�菇�S��蒷���`����S�����������p�`�ɂ��s�b�N�̌����͐��藧���܂��B���̑��p�`����T�AU���������O�p�`�ɂ��s�b�N�̒藝�����藧���܂��B����āA��ʂ̎O�p�`�Ƀs�b�N�̌����͐��藧���܂��B
�y�菇�U�z
�@�����I�ɁA���p�`�̒��_��K���Ɍ��ׂA�������̎O�p�`�ɕ����ł���̂ŁA�s�b�N�̌����͐��藧���܂��B
�m�n5�u����K��v5/19:
04��19����M �X�V5/21
�u�v�ł��B
�����̗���F�R�����g��
![]()
