kadai78

平成１８年１月２９日

[流れ星]

　　　　　第16６回数学的な応募問題解答

　　　　　　＜解答募集期間：1月９日～１月２９日

［平面幾何］

皆さん、今月の２１日２２日大学入試センター試験が全国各地で行われ、新課程の最初の生徒が受験生します。
その中で数学Ⅰ・Ａの科目に「平面幾何」があります。
前日、次のような問題を「上様」から受け取りました。解いてみてください。

問１：三角形ABCの内心をDとしてできる三角形ABD、三角形DBCの内心をそれぞれP,Qとし、
AB=４　BC=８角B＝９０としたときPQの長さを　解き方を添えて答えよ。

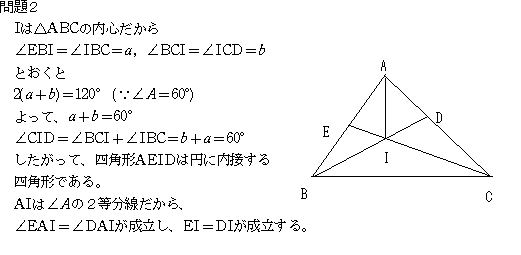
問２：三角形ABCの内心をIとし、角A＝６０゜、直線CIの延長とABの交点をE、直線BIの延長とACの交点をDとした時
EI＝IDを証明せよ。

問３（難）：三角形ABCの内心をI　外心をO　外接円の半径をR　内接円の半径をｒとした時

　　　　　　２Rｒ＝R2乗―OI２乗　　になることを証明せよ。

問４（有名：円に内接する正三角形ABCがあり弧BC（とりあえず短いほうと設定します）上に勝手な点Pを取るとき

　　　　　　PA＝PB+PC　であることを二通りの証明をせよ。

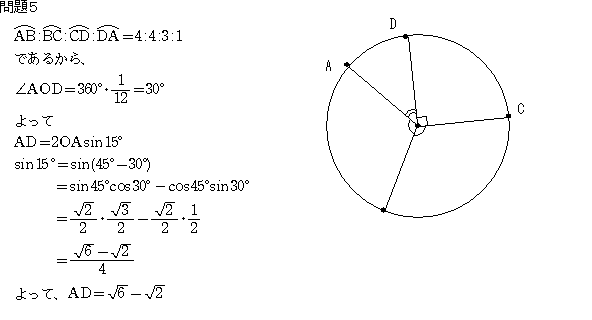
問５：半径２の円周上に４点ABCDを弧AB：弧BC：弧CD：弧DA＝４：４：３：１となるようにとるとき

　　　ADの長さを答えよ。

　　以上、１問２０点で１００点満点。

＜訂正：１月２６日夜に「上様」からありました。問１の問題で、内心を重心にという訂正です。締め切りが間近ということですが、修正前の問題も有効としておきます。この点については、深くお詫びします。＞

問１：三角形ABCの重心をDとしてできる三角形ABD、三角形DBCの重心（１月２９日訂正）をそれぞれP,Qとし、
AB=４　BC=８角B＝９０としたときPQの長さを　解き方を添えて答えよ。

＜問題に関しては、問題３は有名な定理でして、平面図形のオイラーの定理と言われています。２００２年のセンター試験にありました。問題２は鹿児島大学の入試問題（何年かは分かっていないけど）

ＮＯ１「H7K」 1/09　20時07分受信更新1/29

さて，今回の問題ですが……問1がまだ解けていません．困った．
テキストでは記号類が打ちづらいので今回は概略だけです．角度は度数法．

2. a:=∠ABI=∠IBC, b:=∠ACI=∠BCI，a+b=60がすぐわかる．
IからABに下ろした垂線の足をF, ACへの足をGとすると，
FI=GIが成り立つ．これと，∠DIG, ∠FIEを計算すると，両者とも
|30-a|=|30-b|になることから，三角形DGIとEFIは合同．

3. これは中3か高1かのころにやったことがあります．懐かしい．
当時は方べきの定理を覚えてなくて解くのに時間が(1weekほど？)
かかった記憶が．

AIの延長と円Oの交点をPとする．円周角定理とかをひたすら使うと，
BI=CI=PIがわかる．POの延長と円Oの交点をQとし，IからABに引いた
垂線の足をDとすると，三角形AIDとQPBが相似であることがわかる．
BI=PIも使うと，AI*PI=2rRを得る．IOと円Oの交点をX, Y
(I側をXとする)とおく．IO=dとすると，方べきの定理より
R^2-d^2=XI*YI=AI*PI=2rR.

4. 一つめ：三角形ABPをAに中心として60度回転(ACB'に移るとする）すると，
円周角定理などからPCB'は一直線上．これから三角形APB'は正三角形．
よってPA=PB'=PC+CB'=BP+CP.

二つめ：円周角定理を使って，
CP=AB*CR/AR, BP=AB*BR/ARより，BP+CP=AB^2/AR.
一方，円周角定理を何回か使って，
三角形ABPとARB (APとBCの交点をRとおいた)を得る．
これより題意の式が求まる．

5. (三角比は使いたくない，できれば)
求める長さをxとおく．二等辺三角形OADを2枚張り合わせて凧型を作る．
すると，この凧型は1辺1の正三角形と，頂角150度，等辺xの二等辺三角形にわかれる．
これにより，二等辺三角形の面積を2通りの方法で出す．
S = 2*(2/2*2/2) - 2*2*√3/4 = 1/2 * x * x/2
を得るから，これより，x^2=8-4√3．x>0より，x=√6-√2.

ＮＯ２「cbc」 1/11　22時58分受信更新1/29

166回の解答です。よろしくお願いいたします。

問題1はベクトルを使って計算に持ち込んだのですが恐ろしく汚い式になってしまいました。２重根号がはずれず

整理する気にもなりませんでした。

3はベクトルの公式を知っていたのでさほど迷わずできました。ベクトルを利用しないと難問と思います。

今回は各問題を1個の画像で作成しています。（計5枚）

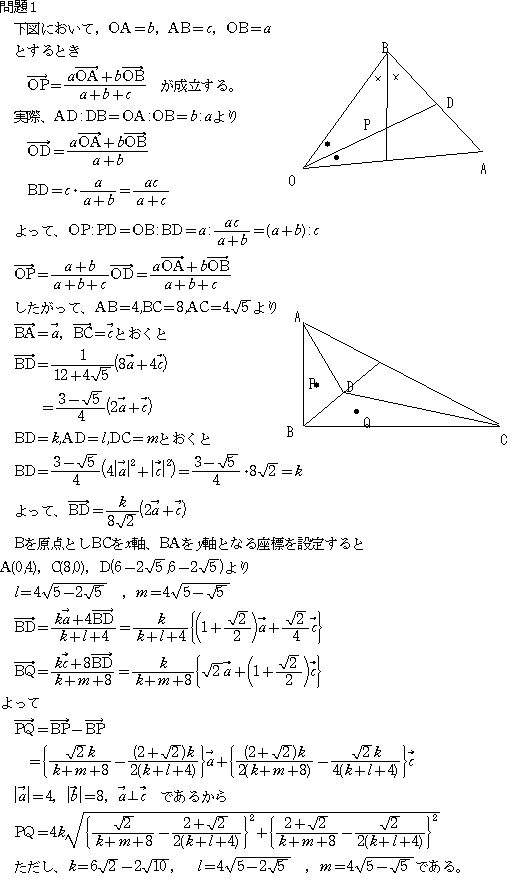
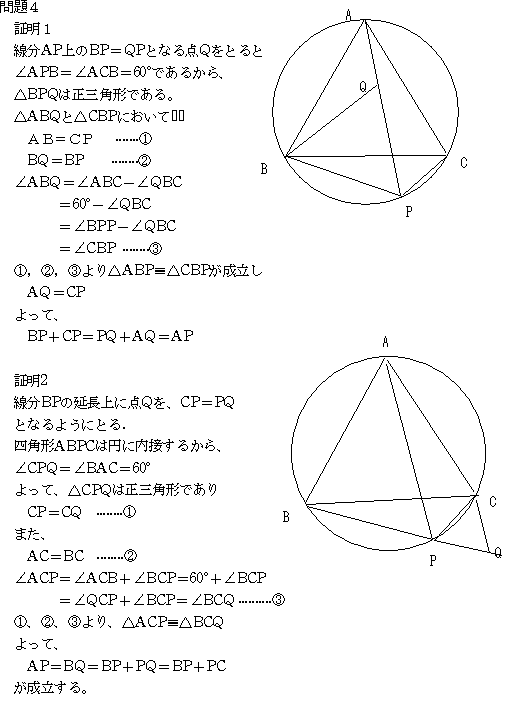
ＮＯ３「Toru」 1/13　17時56分受信更新1/29
あけましておめでとうございます。今年もよろしくお願いします。
新年からなかなか重い問題で、苦労いたしました。
　問１、問５についてはどうも？で途中経過のようになってしまいましたが、一部でもよろしいですからとの言葉に甘えて取りあえず、第1報と言うことで送ってしまいます。　

問２　IからAB,AC へおろした垂線の足をP,Qとする。角B=角Cの時は三角形ABCは正三
角形となり題意は明らかに成り立つので、角B>角C（角B<角Cなら左右反対となるのみ）として、
角B=60+2θ（0<θ<30）とすると、角C=60-2θ
三角形EBCを考えて、角BEC=180-(60+2θ)-(30-θ)=90-θ
三角形DBCを考えて、角BDA=(30+θ)+(60-2θ)=90-θ
よって直角三角形EPIと直角三角形DCIは２角が等しく、対応する辺、IP=IQより合同
となってEI=IDが示された。

問３　外心Oを原点として　A,B,Cの位置ベクトルをα、β、γとし、BC=a,CA=b,AB=c
とすると
ベクトルOI=(aα+bβ+cγ)／(a+b+c)
OI２乗 =(a^2R^2+b^2R^2+c^2R^2+2ab(α,β)+2bc(β,γ)+2ca(γ,α))／(a+b+c)^2
R2乗―OI２乗=(2ab R^2+2bc R^2+ 2ca R^2-(2ab(α,β)+2bc(β,γ)+2ca(γ,α)))
／(a+b+c)^2=(ab((α,α)+(β,β))+bc((β,β)+(γ,γ))+ca((γ,γ)+(α,
α))-(2ab(α,β)+2bc(β,γ)+2ca(γ,α)))／(a+b+c)^2=(ab｜α-β｜^2+bc｜β-γ
｜^2+ca｜γ-α｜^2)／(a+b+c)^2=(abc^2+bca^2+cab^2)／(a+b+c)^2=abc/(a+b+c)

また三角形ABCの面積をSとすれば
r=2S/(a+b+c)
2R=a/sinA=abc/2S (正弦定理と2S=bc sinAより)
から2Rr=abc/(a+b+c)
よって2Rr= R2乗―OI２乗

問４　
解答１）三角形ABPを６０度回転させてABがACに重なるようにして、Pの移り先をQと
すると角ABP+角ACP=180度よりPCQは直線でAP=AQ 角PAQ=60度だから、三角形PAQは正
三角形でAP=PQ,
PQ=PC+CQ=PC+BPより題意は示された。
解答２）角BPA,角CPAはAB,ACに対する円周角で、Pの位置に関わらず60度　角BAP=θ
とすると角ABP=120-θ　角PAC=60-θ 角ACP=60+θ
三角形BAPに正弦定理を使うと　AP/sin(120-θ)=BP/sinθ
三角形APCに正弦定理を使うと　AP/sin(60+θ)=CP/sin(60-θ)
sin(120-θ)=sin(60+θ)=(sinθ+√3 cosθ)/2 sin(60-θ)=(-sinθ+√3 cosθ)/2
よりBP+CP=AP(sinθ+sin(60-θ))/sin (60+θ)=AP

問１　DよりAB,BC,CAへ降ろした垂線の足をK,M,Lとすると
AK=AL,BK=BM,CM=CLより
BK+BM=AB-AK+AC-CM=AB+BC-(AK+CM)=AB+AC-(AL+CL)=AB+BC-CA
からBK=BM=(AB+BC-CA)/2=6-2√5
よってBを原点にBC方向にx軸、BA方向にy軸の座標を置けば
D(6-2√5, 6-2√5)
BD=√2(6-2√5) ,AD^2=(2-2√5)^2+(6-2√5)^2=80-32√5 よりAD=4√(5-2√5)
同様に、CD=4√(5-√5)

前と同じに考えて　Pのy座標Py=(AB+BD-DA)/2=2+√2(3-√5)-2√(5-2√5)
tan 15°=√2-1よりPx=(√2-1) (2+√2(3-√5)-2√(5-2√5))
同様にQx=(BC+BD-CD)/2=4+√2(3-√5)-2√(5-√5)
Qy=(√2-1)(4+√2(3-√5)-2√(5-√5))
とP,Qの座標は求まって
PQ=√((Px-Qx)^2+(Py-Qx)^2)
ですが、これを計算するときれいな形になるものやら？で降参です。
一応エクセルで近似値を求めてみると、1.40697025　となりました。

問５　弧が4:4:3:1であるから1に対する中心角は360°/(4+4+3+1)=30°
AD=2x2sin15°=√6-√2
これでは4:4:3:1の意味がありませんね？

弧でなくて弦だとすれば、
AD=a 、角BCD=θとして　三角形ABDと三角形BCDに余弦定理を適用すると　
a^2+(4a)^2-2a(4a)cos(180-θ)=(3a)^2+(4a)^2-2(3a)(4a)cosθ
からcosθ=1/4 BD=√19 a
半径２の円の中心をOとして三角形ODBを考えると角ODB=2θだから
√19 a/2/2=sinθ=√15/4よってa=√(15/19)

ＮＯ４「uchinyan」1/14　14時28分受信更新1/29
さて、第166回数学的な応募問題の解答、を送ります。
ただ、問1 が、考え方が悪いのでしょうが、どうにも計算ができず、
取り敢えず、近似値を出しました。簡単になるのでしょうか。
「uchinyan」1/27　11時18分受信更新1/29
問題1の修正版に対する解答を追加しました。
添付したもので置き換えてください。
これならば、簡単です ^^v
第166回数学的な応募問題の解答
［平面幾何］できるだけ、初等幾何、それが難しそうな場合は三角関数、を用いた解答に努めました。
問１：三角形ABCの内心をDとしてできる三角形ABD、三角形DBCの内心をそれぞれP,Qとし、
AB=4, BC=8, 角B＝90としたときPQの長さを、解き方を添えて答えよ。
(解答)
△ABC、△ABD、△DBC の内接円の半径をそれぞれ r、p、q とします。
まず、三平方の定理より、AC = 4 * sqrt(5) です。
次に △ABC の面積の関係から、
1/2 * r * (4 + 8 + 4 * sqrt(5)) = 1/2 * 4 * 8
r = 8/(3 + sqrt(5)) = 6 - 2 * sqrt(5) = (sqrt(5) - 1)^2
になります。さらに、∠ABC = 90度に注意すると、三平方の定理を使って、
BD = sqrt(2) * r
AD = sqrt(r^2 + (4-r)^2)
CD = sqrt(r^2 + (8-r)^2)
そこで、△ABD、△DBC の面積の関係から、
1/2 * p * (4 + sqrt(2) * r + sqrt(r^2 + (4-r)^2)) = 1/2 * 4 * r
p = 4r/(4 + sqrt(2) * r + sqrt(r^2 + (4-r)^2))
1/2 * q * (8 + sqrt(2) * r + sqrt(r^2 + (8-r)^2)) = 1/2 * 8 * r
q = 8r/(8 + sqrt(2) * r + sqrt(r^2 + (8-r)^2))
これらと、∠ABP = ∠PBD = ∠DBQ = ∠QBC = 45/2 度より、
BP = p/sin(45/2)
BQ = q/sin(45/2)
となり、△BPQ に余弦定理を用いて、
PQ^2 = BP^2 + BQ^2 - 2 * BP * BQ * cos(∠PBQ)
= BP^2 + BQ^2 - 2 * BP * BQ * cos(45)
= 1/(sin(45/2))^2 * (p^2 + q^2 - sqrt(2) * pq)
ここで、倍角の公式より
、sin(45/2)^2 = (1 - cos(45))/2 = (sqrt(2) - 1)/(2 * sqrt(2))
なので、
PQ^2 = 2 * sqrt(2) * (sqrt(2) + 1) * (p^2 + q^2 - sqrt(2) * pq)
後はこれを計算するだけです。しかし．．．二重根号が外れないなど、どうにも式が簡単になりそうにありません。仕方がないので、取り敢えず、電卓をたたき、近似値を出しておきます。
r = 1.52786404500042
p = 0.674040605314395
q = 0.727088751421737
PQ = 3.67659044315881
(別解)　この方が自然かな。
座標で考えます。A(0,4), B(0,0), C(8,0) とおきます。三平方の定理から、AC = 4 * sqrt(5) です。
BD を D の方に延長した線と AC との交点を E、DP を P の方に延長した線と AB との交点を F、
DQ を Q の方に延長した線と BC との交点を G とします。
すると、BE は ∠ABC の二等分線なので、よく知られた定理から、AE：EC = BA：BC = 1：2 です。
そこで、E(8/3,8/3) になります。
さらに、AD は ∠BAE の二等分線なので、BD：DE = AB：AE = 3：sqrt(5) で、
D(8/3 * 3/(3 + sqrt(5)), 8/3 * 3/(3 + sqrt(5))) = D(6 - 2 * sqrt(5), 6 - 2 * sqrt(5))
になります。今、r = 6 - 2 * sqrt(5) とおいておきます。
この r は、△ABC の内接円の半径になります。
同様のことを
AD = sqrt(r^2 + (4-r)^2)), BD = sqrt(2) * r, CD = sqrt(r^2 + (8-r)^2)
に注意して、F, G を使って P, Q に対しても行うと、
p = 4r/(4 + sqrt(2) * r + sqrt(r^2 + (4-r)^2))
q = 8r/(8 + sqrt(2) * r + sqrt(r^2 + (8-r)^2))
として、
P(p, (sqrt(2) + 1) * p), Q((sqrt(2) + 1) * q, q)
になります。そこで、
PQ^2 = (p - (sqrt(2) + 1) * q)^2 + ((sqrt(2) + 1) * p - q)^2
= (4 + 2 * sqrt(2)) * (p^2 + q^2) - 4 * (sqrt(2) + 1) * pq
= 2 * sqrt(2) * (sqrt(2) + 1) * (p^2 + q^2) - 4 * (sqrt(2) + 1) * pq)
= 2 * sqrt(2) * (sqrt(2) + 1) * (p^2 + q^2 - sqrt(2) * pq)
これは、先ほどの式と同じです。そこで、以下は、先ほどと同じになります。
(感想)かなり素直な解法だと思うのですが、他の問題と比較すると、問３が難しいのはいいとしても、上記の解法の計算の複雑さは異常です。何か、基本的に勘違いしているか、重要なことを見落としているのでしょうか。

修正後の...
問１：三角形ABCの重心をDとしてできる三角形ABD、三角形DBCの重心をそれぞれP,Qとし、AB=4, BC=8, 角B＝90としたときPQの長さを、解き方を添えて答えよ。

(解答)
AD の中点を M とします。重心の性質から、
MP：PA = 1：2, MQ：QC = 1：2
です。したがって、△MPQ ∽ △MAC になり、PQ//AC で PQ = 1/3 * AC です。
三平方の定理より、AC = 4 * sqrt(5) なので、
PQ = 4/3 * sqrt(5)　になります。

(別解)
座標で考えます。A(0,4), B(0,0), C(8,0) とおきます。
重心は、三角形の三点の座標を足して 3 で割って求められるので、
D(8/3,4/3)
P(8/9,16/9)
Q(32/9,4/9)
そこで、
PQ = sqrt((8/9 - 32/9)^2 + (16/9 - 4/9)^2)
= 1/9 * sqrt(24^2 + 12^2)
= 12/9 sqrt(2^2 + 1^2)
= 4/3 * sqrt(5)　　になります。

(感想)
あは、これならば簡単です ^^v

問２：三角形ABCの内心をIとし、角A＝60゜、直線CIの延長とABの交点をE、直線BIの延長とACの交点をDとした時、EI＝IDを証明せよ。
(証明)
AB = AC、AB > AC、AB < AC に場合分けして考えます。
(1) AB = AC の場合
∠BAC = ∠A = 60度なので、△ABC は正三角形です。
したがって、EI ⊥ AB、ID ⊥ AC で、EI = 内接円の半径 = ID になります。
(2) AB > AC の場合
∠BAC = ∠A = 60度なので、∠ABC < 60 < ∠ACB になります。
そこで、BD, CE は ∠ABC, ∠ACB の二等分線なので、∠ABD < 30 < ∠ACE になり、
∠BDA > 90 > ∠CEA となります。そこで、I より AB, AC に垂線を下ろし、
その足を P, Q とすると、P は AE 上に、Q は CD 上にあります。
また、∠DBC + ∠ECB = 1/2 * (180 - ∠BAC) = 60 に注意しておきます。
△IEP, △IDQ において。
IP = 内接円の半径 = IQ, ∠IPE = 90 = ∠IQD です。さらに、
∠IEP= ∠CEA = ∠ABC + ∠ECB = ∠ABD + ∠DBC + ∠ECB = 60 + ∠ABD
= ∠BAC + ∠ABD = ∠BDC = ∠IDQ
よって、△IEP≡△IDQ になります。したがって、EI = ID です。
(3) AB < AC の場合
大小関係が反対になっていることに注意して、AB > AC の場合と同様に証明できます。
(証明終)
(感想)
EI, ID を含む直角三角形の位置関係、向きなどに注意すれば、証明自体は容易です。
∠A = 60度が、ポイントになっていますね。
問３（難）：三角形ABCの内心をI　外心をO　外接円の半径をR　内接円の半径をｒとした時
２Rｒ＝R^2―OI^2 になることを証明せよ。
(証明)
まず特殊な場合、O と I とが一致する場合、を考えます。
このときは、各辺の垂直二等分線がその対角の二等分線に一致するので、△ABC は正三角形です。
したがって、OI = 0, R = 2r ですが、これは、与えられた式を満たします。
次に、O と I とが一致しない場合を考えます。
OI を延長し外接円との交点を I 側を D、O 側を E とします。OD = OE = R です。
このとき、D や E が △ABC の頂点と一致する可能性があります。
そこで、以下を明確にするために、改めて、一致していない頂点、少なくとも一つ存在、であって、
D から反時計回りに最初に現れる点を A とし、さらに反時計回りに B, C としておきます。
次に、A と I とを結び、AI のI の方の延長と外接円との交点を F とします。
さらに、F と O とを結び、FO の O の方の延長と外接円との交点を P とします。PF = 2R です。
また、I から AC に垂線を下ろし、その足を H とします。IH = r です。
さて、△PFB, △IAH において。
∠PBF = ∠R = ∠IHA, ∠FPB = ∠FAB = ∠IAH (円周角及び I は内心) より、△PFB ∽ △IAH です。
そこで、PF：FB = AI：IH で、PF * IH = FB * AI、つまり、2Rr = FB * AI になります。
次に、△FBI において。円周角と I が内心であることから、
∠FBI = ∠FBC + ∠CBI = ∠FAC + ∠CBI = ∠BAI + ∠ABI = ∠FIB なので、FB = FI です。
そこで、2Rr = FI * AI になります。
さらに、△FEI, △DAI において。
∠FEI = ∠FED = ∠FAD = ∠IAD (円周角), ∠FIE = ∠DIA (対頂角) なので、
△FEI ∽ △DAI になります。そこで、FI：DI = EI：AI で FI * AI = DI * EI です。
そこで、2Rr = DI * EI になります。ここで、
DI = DO - OI = R - OI, EI = EO + OI = R + OI
なので、
2Rr = DI * EI = (R - OI) * (R + OI) = R^2 - OI^2
になります。
(証明終)
(感想)これは確かに難しいです。ただ、それなりに有名な結果ではないのでしょうか。実は、ここで書いた証明は、残念ながら私のオリジナルではありません。私がまだ学生の頃、30年以上前、に一度、比較的最近、といっても1年ぐらい前かな、にもう一度、本か雑誌かで定理として証明を読んだ記憶があります。どちらも証明自体は忘れてしまいましたが、1年ぐらい前の方は、補助線の引き方をある程度覚えていたので、それをもとに再構成しました。初等幾何は、図形の位置関係で場合分けが必要になります。気付いた範囲で、それも意識したつもりですが、抜けがないとは言い切れない点が心配です。

問４（有名）：円に内接する正三角形ABCがあり弧BC（とりあえず短いほうと設定します）上に勝手な点Pを取るとき、PA＝PB+PC、であることを二通りの証明をせよ。

(証明1)
PA 上に P から PD = PB となるような点 D をとります。
すると、円周角より ∠BPD = ∠BPA = ∠BCA = 60度なので、△PBD は正三角形です。
△DAB, △PCB において。
AB = CB, ∠DAB = ∠PAB = ∠PCB (円周角),
∠DBA = ∠ABC - ∠CBD = 60 - ∠CBD = ∠PBD - ∠CBD = ∠PBC
なので、△DAB ≡ △PCB になり、DA = PC になります。
そこで、PA = PD + DA = PB + PC です。
(証明1終)
(証明2)
PB を P の方に延長しその上に PD = PC となるような点 D をとります。
□ABPC は円に内接しているので ∠CPD = ∠ABC = 60度で、△PCD は正三角形です。
△PAC, △DBC において。
AC = BC, ∠PAC = ∠PBC = ∠DBC (円周角),
∠PCA = ∠PCB + ∠BCA = ∠PCB + 60 = ∠BCP + ∠PCD = ∠BCD
なので、△PAC ≡ △DBC になり、PA = DB = BD になります。
そこで、PA = BD = PB + PC です。
(PC の延長を考えても同様に証明できます。)
(証明2終)

(証明3)
三角関数を使います。今、∠BAP = x とします。
すると、円周角より、∠APB = ∠ACB = 60度、∠APC = ∠ABC = 60度なので、
∠ABP = 180 - 60 - x = 120 - x, ∠ACP = 180 - 60 - (60 - x) = 60 + x
になります。
そこで、△ABP, △ACP に正弦定理を用いて
PA/sin(120-x) = PB/sin(x), PA/sin(60+x) = PC/sin(60-x)
PB = sin(x)/sin(120-x) * PA, PC = sin(60-x)/sin(60+x) * PA
ここで、sin(120-x) = sin(180-(120-x)) = sin(60+x) なので、
PB + PC = PA * (sin(x) + sin(60-x))/sin(60+x)
sin の和の公式を使うと、
sin(x) + sin(60-x) = sin(60-x) + sin(x) = 2 * sin(30) * cos(30-x) = cos(30-x)
さらに、90度ずらして cos を sin に変換すると
cos(30-x) = sin(90-(30-x)) = sin(60+x)
したがって、
PB + PC = PA * sin(60+x)/sin(60+x) = PA
(証明3終)
(感想)　これは易しい。座標やベクトルでもできるかもしれませんが、ルートが出てきて気持ちが悪いので避けました (^^;

問５：半径２の円周上に４点ABCDを弧AB：弧BC：弧CD：弧DA＝４：４：３：１となるようにとるとき、ADの長さを答えよ。
(解答)
円の中心を O とします。
四点 A, B, C, D の位置関係を考えてみると、円周上に A, B, C, D の順番に並ぶ場合、
しかないようです。
そこで、四点は360度を 4：4：3：1 に分けることになるので、
弧DA に対する中心角は 360/(4 + 4 + 3 + 1) = 30度になります。
そこで、△OAD に余弦定理を使って、
AD = sqrt(2^2 + 2^2 - 2 * 2 * 2 * cos(30)) = sqrt(8 - 4 * sqrt(3))
= sqrt(2) * sqrt(4 - 2 * sqrt(3))
= sqrt(2) * (sqrt(3) - 1)
= sqrt(6) - sqrt(2)
(感想)うーむ、簡単すぎる気が．．．引っ掛け問題なのかな？　他の位置関係があるのかな？なお、最後のところは、sin(15) = (sqrt(6) - sqrt(2))/2 を使えば　AD = 2 * sin(15) = 2 * (sqrt(6) - sqrt(2))/2 = sqrt(6) - sqrt(2)
とやってもよく、さらに、△OAD を OD に関して折り返し A の移動先を B として、△OAB が正三角形になることを利用する方法もあります。この場合は、AB と OD との交点を H とすると、AH = 1, OH = sqrt(3) なので、三平方の定理より、
AD = sqrt(AH^2 + (OD - OH)^2) = sqrt(1^2 + (2 - sqrt(3))^2) = sqrt(8 - 4 * sqrt(3))
で、後は、(解答)と同じです。

ＮＯ５「ICE」 1/15　22時24分受信更新1/29
166回の解答をお送りします。
(1)はうまい方法が思いつきませんでした。
計算をやる気力がでなかったので、パスします。
数学の問題を集めたWEBページを作りました。
http://www13.plala.or.jp/wonder3/
WEBや本などで見つけた、おもしろそうな問題を載せています。
（私自身はほとんど解けていませんが）気が向いたら、解いてみてください。