平成１８年６月１０日
[流れ星]
第1７３回数学的な応募問題解答
＜解答募集期間：５月１４日〜６月１１日
［３点を通る放物線］
皆さん、前回の件は大変失礼しました。今回は生徒からの質問です。
点Ａ（１，−２）から放物線 ｙ＝ｘ２へ２本の接線を引き、接点をそれぞれＢ，Ｃとする。このとき、３点Ａ，Ｂ，Ｃを通る放物線の方程式を求めよ。できたらエレガントな解答を考えてください。
ＮＯ１「uchinyan」5/15 11時32分受信 更新6/10
＜コメント：うーんと、何がエレガントと思うかは、個人差がありそうなので、取り敢えず、思いついた解法を上げておきます。＞
第１７３回数学的な応募問題への解答
［３点を通る放物線］
(解法1)
まずは、例によって、地道にやってみます。
接線の傾きを m とすると、接線は、点 A(1.-2) を通ることから、
y - (-2) = m * (x - 1)
y = m * x - m - 2
になります。これが、y = x^2 と接するには、y を消去した x の二次方程式
x^2 - m * x + m + 2 = 0
が重解、重根、をもてばいいです。そこで、判別式 = D = 0 より、
D = m^2 - 4m - 8 = 0
これは、明らかに、二つの異なる実数解をもちます。そしてそのときに、もとの x の二次方程式は、
x = m/2 となる重解をもちます。この x を改めて t とおくと、m = 2t なので、
t^2 - 2t - 2 = 0
になります。この解が、接点の x 座標です。これを α, β とおくと、明らかに等しくなく、
解と係数の関係から、
α + β = 2, αβ = -2
になります。以下では、これをフルに使います。
さて、ここまで分かれば、求める放物線の方程式を y = a * x^2 + b * x + c とおいて、
これが A(1,-2), B(α,α^2), C(β,β^2) を通る条件から、a, b, c を決定するだけです。つまり、
a + b + c = - 2
a * α^2 + b * α + c = α^2
a * β^2 + b * β + c = β^2
最初の式から、
c = - a - b - 2
なので、c を消去すると、
a * (α^2 - 1) + b * (α - 1) = α^2 + 2
a * (β^2 - 1) + b * (β - 1) = β^2 + 2
二式を足し算して、
a * (α^2 + β^2 - 2) + b * (α + β - 2) = α^2 + β^2 + 4
a * ((α + β)^2 - 2αβ - 2) + b * ((α + β) - 2) = (α + β)^2 - 2αβ + 4
a * (2^2 - 2 * (-2) - 2) + b * (2 - 2) = 2^2 - 2 * (-2) + 4
6 * a = 12
a = 2
一方、二式を引き算して、
a * (α^2 - β^2) + b * (α - β) = α^2 - β^2
α not= β なので、
a * (α + β) + b = α + β
2 * a + b = 2
b = - 2
そこで、
c = - 2
結局、求める放物線の方程式は、
y = 2 * x^2 - 2 * x - 2
になります。
(解法2)
もし、微分を知っていれば、y' = 2x なので、接点を (t,t^2) とおいて、接線の方程式が
y - t^2 = 2t * (x - t)
y = 2t * x - t^2
とかけるので、これが、A(1,-2) を通ることから、上式で x = 1, y = -2 として、
t^2 - 2t - 2 = 0
が得られます。後は、(解法1)と同じにやればいいです。
(解法3)
接点の x 座標を与える方程式
t^2 - 2t - 2 = 0
を導くまでは、(解法1)や(解法2)と同じとします。この後の放物線の方程式の求め方を工夫します。
放物線の方程式を
y = a * (x-α)(x-β) + b * ((x-α) + (x-β)) + c
とおいてみます。このとき、B(α,α^2), C(β,β^2) を通る条件から、
+ b * (α - β) + c = α^2
- b * (α - β) + c = β^2
これら二式を足して
2 * c = α^2 + β^2 = (α + β)^2 - 2αβ = 2^2 - 2 * (-2) = 8
c = 4
これら二式を引いて、α not= β にも注意して、
2 * b * (α - β) = α^2 - β^2 = (α + β) * (α - β)
2 * b = α + β = 2
b = 1
そこで、放物線の方程式は、
y = a * (x-α)(x-β) + ((x-α) + (x-β)) + 4
y = a * (x^2 - (α+β) * x + αβ)
+ 2 * x - (α+β) + 4
y = a * (x^2 - 2 * x - 2) + 2 * x - 2 + 4
y = a * (x^2 - 2 * x - 2) + 2 * x + 2
A(1,-2) を通ることから、
- 2 = a * (1 - 2 - 2) + 2 + 2
a = 2
そこで、
y = 2 * x^2 - 2 * x - 2
になります。
(解法4)
接点の x 座標を与える方程式
t^2 - 2t - 2 = 0
を導くまでは、(解法1)や(解法2)と同じとします。この後の放物線の方程式の求め方を、さらに、工夫します。
放物線の方程式を
y = a * (x-α)(x-β) + b * x^2 + c
とおいてみます。このとき、B(α,α^2), C(β,β^2) を通る条件から、
b * α^2 + c = α^2
b * β^2 + c = β^2
これら二式を引いて、α not= β にも注意して、
b * (α^2 - β^2) = α^2 - β^2
b = 1
これら二式を足して
b * (α^2 + β^2) * c = α^2 + β^2
(α^2 + β^2) * c = α^2 + β^2
c = 0
そこで、放物線の方程式は、
y = a * (x-α)(x-β) + x^2
y = a * (x^2 - (α+β) * x + αβ)
+ x^2
y = a * (x^2 - 2 * x - 2) + x^2
A(1,-2) を通ることから、
- 2 = a * (1 - 2 - 2) + 1
a = 1
そこで、
y = 2 * x^2 - 2 * x - 2
になります。
(解法5)
接点の x 座標を与える方程式
t^2 - 2t - 2 = 0
を導くまでは、(解法1)や(解法2)と同じとします。この後の放物線の方程式の求め方を、さらに、工夫します。
一般に、二つの曲線 y = f(x), y = g(x) の共有点を通る曲線は、
p * (f(x) - y) + q * (g(x) - y) = 0
と書けます。これは、明らかだと思います。これを使います。
まず、二つの接点 B(α,α^2), C(β,β^2) を通る直線を求めておきます。これは、α not= β なので、
y - α^2 = (α^2 - β^2)/(α - β) * (x - α)
y = (α + β) * x - αβ
y = 2 * x + 2
そこで、B(α,α^2), C(β,β^2) が y = x^2 と y = 2 * x + 2 の共有点であることから、
求める放物線の方程式は、
p * (x^2 - y) + q * (2 * x + 2 - y) = 0
と書けます。これが、A(1,-2) を通ることから、
3 * p + 6 * q = 0
p = - 2 * q
そこで、
q * (- 2 * x^2 + 2 * x + 2 + y) = 0
q = 0 は p = 0 で意味がないので、結局、求める放物線の方程式は、
y = 2 * x^2 - 2 * x - 2
になります。
(解法6)
ふと気付いたのですが、(解法4)の方向は、かなり一般化できるようです。
今、y = f(x) に、点 A(p,q) から接線を引くことを考えます。
接点を T(t,f(t)) とすると、接線の方程式は、
y - f(t) = f'(t) * (x - t)
これが、点 A(p,q) を通るので、
q - f(t) = f'(t) * (p - t)
f'(t) * (t - p) - f(t) + q = 0
になります。ここで、次の式を考えます。
y = g(x) = (f'(x) * (x - p) - f(x) + q) + f(x)
すると、
g(t) = (f'(t) * (t - p) - f(t) + q) + f(t) = 0 + f(t) = f(t)
g(p) = (f'(p) * (p - p) - f(p) + q) + f(p) = q
つまり、y = g(x) は、点 A(p,q) 及び T(t,f(t))
を通ります！
したがって、
y = g(x) = (f'(x) * (x - p) - f(x) + q) + f(x)
y = f'(x) * x - f'(x) * p + q
が、求める曲線の方程式になっています。
今回の問題では、f(x) = x^2, p = 1, q = -2 なので、結局、
y = 2 * x^2 - 2 * x - 2
になります。
(感想)
取り敢えず、求める放物線の方程式の置き方を工夫してみましたが、
(解法4)が少し気になり、再検討して(解法6)が得られました。ちょっと驚きです。
なお、点 B と C の x 座標の中点が A の x 座標になっています。
これは、接線の式から明らかで、放物線ではよく知られた性質です。
一部の計算にもこの性質が現れていますが、(解法1)で a が直接に求まる辺り、図形的考察を加えてさらに何か考えられるかもしれません
ＮＯ２「kashiwagi｣5/16 07時28分受信 更新6/10
<コメント：お世話になります。早速の変更問題どうも有難うございました。通常は三点の値を 代入し連立方程式を解くのでしょうが、エレガントな解法とありましたので敢えて、根と 面積の関係や微分係数、面積比及び接線の性質などを使ってみました。
どうも時間はかかるし、連立方程式の方が早いですね。他の方々のエレガントな解法 に期待致します。＞
72解答
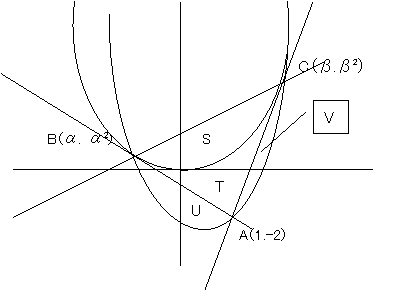題意より右の図が描けます。
S〜Vは直線や放物線で囲まれた面積です。
点Aを通る接線を
とおくと、
この方程式が重根を持つことから
判別式が0
これより
このとき2次方程式の
重根は
即ちα＝
β＝
ところで、面積SとTの間にはS＝2Tの関係がある。又、直線と曲線で囲まれた部分の面積Sは、
S＝
＝
、因ってS＝2TよりT＝
即ち、S+T＝
ここでA,B及びCの3点を通る放物線を
と置くと、先ほどと同様に
S+T+U+V=＝
同様にしてU=V=
であるからU+V=
これらよりS+T＝＝-＝
となる。
は題意より当然正の数であるから ＝2となる。
次にB,Cを通る直線の勾配をみると
である。
ところで放物線の性質より点Aに於ける接線の勾配に直線BCの勾配は等しいので微分係数を使い
の
に1を代入した値は2であるから
-2となる。
最後に、この放物線は点A（1.-2）を通るので値を代入し、
-2を得る。
以上より求める放物線は
となる。
ＮＯ３「Toru」 5/16 13時08分受信 更新6/10
＜コメント：エレガントな解法というのには程遠いようですがとりあえず。どうも最近ねばりがなくなっているようですが、ままならず。
この機会に、２次曲線というのを少し復習してみようと思いましたが、こちらも中途半端です。 ＞
y=x^2 の(p,p^2)での接線はy=2px-p^2でこれが(1,-2)を通るとして、
B(1-√3,4-2√3) C(1+√3,4+2√3)
X=x-1 ,Y=y+2 ---1) としてAを原点に移動すると B(-√3,6-2√3) C(√3,6+2√3)
原点を通る放物線の方程式を
(aX+bY)^2+cX+dY=0 (ad-bc≠0) として、これに B,Cを代入して計算すると
(6b±√3(a+2b))^2+(6d±√3(c+2d))=0
36b^2+3(a+2b)^2+6d±√3(12b(a+2b)+c+2d)=0
3a^2+12ab+48b^2+6d±√3(12ab+24b^2+c+2d)=0
この二つの式を足したり引いたりすると
3a^2+12ab+48b^2+6d=0, 12ab+24b^2+c+2d=0
よりd=-(a^2+4ab+16b^2)/2, c=a^2-8ab-8b^2
1)を代入して
(ax+by)^2-(a^+4ab+8b^2)x-(a^2/2+4ab+4b^2)y −a^2-4b^2=0
ただし(ad-bc≠0)よりa^3+6a^2b-16b^3≠0
たとえば、a=1,b=0としてみると、
x^2-x-y/2-1=0 より y=2(x^2-x-1)
a=0, b=1なら y^2-8x-4y-4=0よりx=y^2/8-y/2-1/2
a=2,b=-1なら 4x^2-4xy+y^2-4x+2y-8=0 などなどです。
