平成18年8月20日
 [流れ星]
[流れ星]
第176回数学的な応募問題解答
<解答募集期間:7月30日〜8月20日
[ゲームの引き際]
皆さん、賭け事のゲームをしていて、いつやめるかの引き際を考えたことはありませんか。
『A』 ここに、目が自然数の1から6までの正6面体のサイコロがあります。
問題1:正6面体のサイコロを1回または2回振り、最後に出た目の数を得点とするゲームを考える。1回振って出た目を見たうえで2回目を振るか否かを決めるのである。どのように引き際を判断すると良いか。
問題2:上と同様のゲームを3回振ることが可能なら、2回目、3回目を振るか否かの決定は、どのようにするに引き際を判断すると有利か。また、このゲームで得点の100倍のお金がもらえるとき、掛け金400円を払って挑戦するのは得か損か。
さて、『B』今度は目が自然数の1から20までの正二十面体のサイコロに変えます。
問題3:正20面体サイコロを1回または2回振り、最後に出た目の数を得点とするゲームを考える。1回振って出た目を見たうえで2回目を振るか否かを決めるのである。どのように引き際を判断すると良いか。
問題4:上と同様のゲームを3回振ることが可能なら、2回目、3回目を振るか否かの決定は、どのように引き際を判断すると良いか。
問題5:さらに、上と同様のゲームを5回振ることが可能なら、2回目、3回目、4回目、5回目を振るか否かの決定は、どのように引き際を判断すると良いか。
また、このゲームに得点の100倍のお金がもらえるとき、掛け金1500円を払って挑戦するのは得か損か。
NO1「uchinyan」8/03 13時58分受信
更新
「uchinyan」8/03 18時34分受信 更新
「uchinyan」8/06 11時27分受信 更新8/20
第176回数学的な応募問題
[ゲームの引き際]
一度、解答を提出したのですが、間違っていたようなので、水の流れ先生のご指導を受けて、再考しました。
問題1:
通常の正6面体のサイコロなので、1回振った場合の出る目の期待値は、
1 * 1/6 + 2 * 1/6 + 3 * 1/3 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6
= 21/6 = 7/2 = 3.5
つまり、1回振るごとに 3.5 の目が出ると期待できます。そこで、
・今出ている目が 3.5 よりも小さければ、もう1回振ってそれよりも大きな目が出る可能性が高い。
・今出ている目が 3.5 よりも大きければ、もう1回振ってそれよりも大きな目が出る可能性が低い。
と考えられます。
したがって、
・1回目の目が 1, 2, 3 ならば、2回目を振る。
・1回目の目が 4, 5, 6 ならば、2回目を振らない。という戦略が妥当だと思います。
問題2:
2回目にサイコロを振った後の時点では、問題1:の戦略を取るのが妥当です。つまり、
・2回目の目が 1, 2, 3 ならば、3回目を振る。
・2回目の目が 4, 5, 6 ならば、3回目を振らない。
そこで、2回目を振った場合にはこの戦略を取るとして、2回目を振るべきかどうかを検討します。
この場合の2回目以降の出る目の期待値は、
3/6 * (1 * 1/6 + 2 * 1/6 + 3 * 1/3 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6) + 4 * 1/6 + 5
* 1/6 + 6 * 1/6
3/6 * 7/2 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6
= 7/4 + 5/2 = 17/4 = 4.25
になります。つまり、1回目を振った後で、さらに振った場合の出る目は 4.25 が期待されます。
そこで、
・1回目の目が 1, 2, 3, 4 ならば、2回目を振る。
・1回目の目が 5, 6 ならば、2回目を振らない。という戦略が妥当になります。
結局、戦略をまとめると、
・1回目の目が 1, 2, 3, 4 ならば、2回目を振る。
・2回目の目が 1, 2, 3 ならば、3回目を振る。
・2回目の目が 4, 5, 6 ならば、3回目を振らない。
・1回目の目が 5, 6 ならば、2回目を振らない。となります。
この戦略をとった場合、得られる金額の期待値は、
(4/6 * 17/4 + (5 * 1/6 + 6 * 1/6)) * 100
= (17/6 + 11/6) * 100
= 14/3 * 100
= 466 + 2/3 円
これは 400 円よりも多いので、挑戦する方が得になります。
問題3:
正20面体のサイコロなので、1回振った場合の出る目の期待値は、
1 * 1/20 + 2 * 1/20 + ... + 19 * 1/20 + 20 * 1/20
= 20 * 21 * 1/2 * 1/20 = 21/2 = 10.5
つまり、1回振るごとに 10.5 の目が出ると期待できます。そこで、
・今出ている目が 10.5 よりも小さければ、もう1回振ってそれよりも大きな目が出る可能性が高い。
・今出ている目が 10.5 よりも大きければ、もう1回振ってそれよりも大きな目が出る可能性が低い。
と考えられます。
したがって、、
・1回目の目が 1, 2, ..., 9, 10 ならば、2回目を振る。
・1回目の目が 11, 12, ..., 19, 20 ならば、2回目を振らない。という戦略が妥当だと思います。
問題4:
問題2:と同様に考えられます。
2回目にサイコロを振った後の時点では、問題3:の戦略を取るのが妥当です。つまり、
・2回目の目が 1, 2, ..., 9, 10 ならば、3回目を振る。
・2回目の目が 11, 12, ..., 19, 20 ならば、3回目を振らない。
そこで、2回目を振った場合にはこの戦略を取るとして、2回目を振るべきかどうかを検討します。
この場合の2回目以降の出る目の期待値は、
10/20 * 21/2 + 11 * 1/20 + 12 * 1/20 + ... + 19 * 1/20 + 20 * 1/20
= 21/4 + 155/20 = 21/4 + 31/4 = 13
になります。つまり、1回目を振った後で、さらに振った場合の出る目は 13 が期待されます。
そこで、
・1回目の目が 1, 2, ..., 12 ならば、2回目を振る。
・1回目の目が 13, 14, ..., 19, 20 ならば、2回目を振らない。
又は
・1回目の目が 1, 2, ..., 12, 13 ならば、2回目を振る。
・1回目の目が 14, 15, ..., 19, 20 ならば、2回目を振らない。
という戦略が考えられます。どちらを選んでもOKです。念のために確認しておくと...
前者の出る目の期待値を求めてみると、
12/20 * 13 + 13 * 1/20 + 14 * 1/20 + ... + 19 * 1/20 + 20 * 1/20
= 39/5 + 132/20 = 39/5 + 33/5 = 72/5 = 14.4
一方、後者の出る目の期待値は、
13/20 * 13 + 14 * 1/20 + 15 * 1/20 + ... + 19 * 1/20 + 20 * 1/20
= 169/20 + 119/20 = 288/20 = 72/5 = 14.4
で、一致します。
結局、戦略をまとめると、
・1回目の目が 1, 2, ..., 12 ならば、2回目を振る。
・2回目の目が 1, 2, ..., 9, 10 ならば、3回目を振る。
・2回目の目が 11, 12, ..., 19, 20 ならば、3回目を振らない。
・1回目の目が 13, 14, ..., 19, 20 ならば、2回目を振らない。
又は
・1回目の目が 1, 2, ..., 12, 13 ならば、2回目を振る。
・2回目の目が 1, 2, ..., 9, 10 ならば、3回目を振る。
・2回目の目が 11, 12, ..., 19, 20 ならば、3回目を振らない。
・1回目の目が 14, 15, ..., 19, 20 ならば、2回目を振らない。
のどちらかを選択すればいいことになります。
なお、このときの出る目の期待値は、いずれの戦略でも 72/5 になります。
問題5:
同様に考えます。まず、4回振ることができる場合です。
2回目にサイコロを振った後の時点では、問題4:の戦略を取るのが妥当です。つまり、
・2回目の目が 1, 2, ..., 12 ならば、3回目を振る。
・3回目の目が 1, 2, ..., 9, 10 ならば、4回目を振る。
・3回目の目が 11, 12, ..., 19, 20 ならば、4回目を振らない。
・2回目の目が 13, 14, ..., 19, 20 ならば、3回目を振らない。
又は
・2回目の目が 1, 2, ..., 12, 13 ならば、3回目を振る。
・3回目の目が 1, 2, ..., 9, 10 ならば、4回目を振る。
・3回目の目が 11, 12, ..., 19, 20 ならば、4回目を振らない。
・2回目の目が 14, 15, ..., 19, 20 ならば、3回目を振らない。
そこで、2回目を振った場合にはこのどちらかの戦略を取るとして、2回目を振るべきかどうかを検討します。
この場合の2回目以降の出る目の期待値は、どちらの戦略を取っても 72/5 = 14.4 でした。
つまり、1回目を振った後、さらに振った場合の出る目は 14.4 が期待されます。
そこで、
・1回目の目が 1, 2, ..., 12, 13, 14 ならば、2回目を振る。
・1回目の目が 15, 16, ..., 19, 20 ならば、2回目を振らない。という戦略が妥当になります。
結局、戦略をまとめると、
・1回目の目が 1, 2, ..., 12, 13, 14 ならば、2回目を振る。
・2回目の目が 1, 2, ..., 12 ならば、3回目を振る。
・3回目の目が 1, 2, ..., 9, 10 ならば、4回目を振る。
・3回目の目が 11, 12, ..., 19, 20 ならば、4回目を振らない。
・2回目の目が 13, 14, ..., 19, 20 ならば、3回目を振らない。
・1回目の目が 15, 16, ..., 19, 20 ならば、2回目を振らない。
又は
・1回目の目が 1, 2, ..., 12, 13, 14 ならば、2回目を振る。
・2回目の目が 1, 2, ..., 12, 13 ならば、3回目を振る。
・3回目の目が 1, 2, ..., 9, 10 ならば、4回目を振る。
・3回目の目が 11, 12, ..., 19, 20 ならば、4回目を振らない。
・2回目の目が 14, 15, ..., 19, 20 ならば、3回目を振らない。
・1回目の目が 15, 16, ..., 19, 20 ならば、2回目を振らない。のどちらかを選択すればいいことになります。
なお、この戦略をとった場合の出る目の期待値は、
2回目以降の出る目の期待値がどちらの戦略でも 72/5 だったので、
14/20 * 72/5 + 15 * 1/20 + 16 * 1/20 + ... + 19 * 1/20 + 20 * 1/20
= 252/25 + 105/20
= 252/25 + 21/4
= (1008 + 525)/100
= 1533/100
になります。
次に、5回振ることができる場合です。
2回目にサイコロを振った後の時点では、4回振ることができた場合の戦略を取るのが妥当です。
そこで、2回目を振った場合にはこの方針を取るとして、2回目を振るべきかどうかを検討します。
この場合の2回目以降の出る目の期待値は、1533/100 = 15.33 でした。
つまり、1回目を振った後、さらに振った場合の出る目は 15.33 が期待されます。
そこで、
・1回目の目が 1, 2, ..., 12, 13, 15 ならば、2回目を振る。
・1回目の目が 16, 17, 18, 19, 20 ならば、2回目を振らない。という戦略が妥当になります。
結局、戦略をまとめると、
・1回目の目が 1, 2, ..., 12, 13, 15 ならば、2回目を振る。
・2回目の目が 1, 2, ..., 12, 13, 14 ならば、3回目を振る。
・3回目の目が 1, 2, ..., 12 ならば、4回目を振る。
・4回目の目が 1, 2, ..., 9, 10 ならば、5回目を振る。
・4回目の目が 11, 12, ..., 19, 20 ならば、5回目を振らない。
・3回目の目が 13, 14, ..., 19, 20 ならば、4回目を振らない。
・2回目の目が 15, 16, ..., 19, 20 ならば、3回目を振らない。
・1回目の目が 16, 17, 18, 19, 20 ならば、2回目を振らない。
又は
・1回目の目が 1, 2, ..., 12, 13, 15 ならば、2回目を振る。
・2回目の目が 1, 2, ..., 12, 13, 14 ならば、3回目を振る。
・3回目の目が 1, 2, ..., 12, 13 ならば、4回目を振る。
・4回目の目が 1, 2, ..., 9, 10 ならば、5回目を振る。
・4回目の目が 11, 12, ..., 19, 20 ならば、5回目を振らない。
・3回目の目が 14, 15, ..., 19, 20 ならば、4回目を振らない。
・2回目の目が 15, 16, ..., 19, 20 ならば、3回目を振らない。
・1回目の目が 16, 17, 18, 19, 20 ならば、2回目を振らない。
のどちらかを選択すればいいことになります。
そして、この戦略をとった場合の出る目の期待値は、
2回目以降の出る目の期待値がどちらの戦略でも 1533/100 だったので、
(15/20 * 1533/100 + 16 * 1/20 + 17 * 1/20 + 18 * 1/20 + 19 * 1/20 + 20 * 1/20)
* 100
= (4599/400 + 90/20) * 100
= (4599 + 1800)/400 * 100
= 6399/4
= 1599.75 円
になります。
これは 1500 円よりも多いので、挑戦する方が得になります。
(感想)
最初単純に、各回ごとにその回の目とその次の出る目の期待値とを比較して判断する戦略をよしとしていました。
しかし、水の流れさんに、ある回における戦略は、その後の出る目の可能性の連鎖を考慮しなければならないことを指摘されて、
誤りであることを認識し、再考しました。
この戦略でいくと、無限回振れる場合には、ある回以降に出る目の期待値はサイコロの最大の目になります。
一見奇妙な気もしたのですが、要は、何回でも振れる場合には、サイコロの最大の目が出るまで振り続けることが可能なので、この考えは、常識的にも妥当です。
No2「スモークマン」 8/04 16時10分受信 更新8/20
前回は意味がわからなかったです。。。(^^)
今回は単純に(常識的に)考えましたが、、、まずいのかなあ??
問題1
単純に、毎回目の出方は独立なので、
1+2+...+6=21,21/6=3.5
よって、1回目が3以下ならもう一回振る。4以上なら止める。
<水の流れコメント:正解です>」
問題2
4以上がでるまで振る。
4以上になる確率は、1/2
(4+5+6)/3*1/2*100=250<400
だから損。
<水の流れコメント: 期待値の計算になっていないのでは>」
問題3
(1+2+・・・+20)/20=10.5
なので、10以下なら振り、11以上なら止める。
<水の流れコメント:正解です>」
問題4
11以上がでるまで振る。
問題5
11以上がでるまで振る。
(11+12+・・・+20)/10*1/2*100=775
だから、損。
<水の流れコメント:以後は、以下問題2のヒントを参考に。
私の考え方;最後の3回目を振るかどうかから最初考えます。
<ステップ1> 3回目までサイコロを振った場合の得点の期待値は
(3日目に出た目の数だけで決まるので)7/2=3.5になります。
したがって、(1回目に出た目が”あまりよくなかった”ために)2回目を振った場合に出た目の数は
3以下であったなら、3日目を振った方が有利であり、
4以上であったなら、2回目をやめておいた方が有利です。
<ステップ2> 次に、2回目を振るか否か、1回目に出た目によってどのように判断すると良いかを調べる。
NO3「Toru」 8/07 14時29分受信 更新8/20
数学的にはやはり期待値で考えるのでしょう。
(A)
問題1 サイコロを1回振った時の得点の期待値
は1x1/6+2x1/6+3x1/6+4x1/6+5x1/6+6x1/6=3.5
よって1回めに3.5より大きい目すなわち4,5,6が出れば、2回目は振らない。
1回めに3.5より小さい目すなわち1,2,3が出れば、2回目を振る。
問 題 2 問題1の規則に従って1or2回 振った時の得点の期待値をもとめる。
得点が4(,5,6)となる確率はそれぞれ、1回目に4(,5,6)が出るか、1回目は1,2,3
のいずれか出で2回目に4(,5,6)がでる場合で、1/6+1/2x1/6=1/4
得点が1(,2,3)となる確率は 1回目に1,2,3のいずれかが出て、2回目に1(,2,3)がでる場合で、1/2x1/6=1/12
よって期待値は1x1/12+2x1/12+3x1/12+4x1/4+5x1/4+6x1/4=4.25
よって、3回振ることが可能な場合は
1回目が5,6なら終わり、1,2,3,4なら2回目へ、2回目が4,5,6なら終わり、1,2,3なら3回目へとする。
またこの規則によって行った場合の期待値は
得点5,6の確率は1/6+2/3x1/6+2/3x1/2x1/6=1/3
得点4の確率は 2/3x1/6+2/3x1/2x1/6=1/6
得点1,2,3の確率は2/3x1/2x1/6=1/18
より1x1/18+2x1/18+3x1/18+4x1/6+5x1/3+6x1/3=14/3=4.66- - ->4
だから400円はらって挑戦するのは得と考えられる。
(B)
問題3 正20面体のさいころを1回振った時に出る目の期待値は
1x1/20+2x1/20+-------+20x1/20=10.5
より1〜10なら2回目を振る。11〜20なら1回で止めておく。
問題4 上記の方針で2回目まで触れる場合の得点の期待値は
1〜10 の確率がそれぞれ1/2x1/20=1/40
11〜20の確率がそれぞれ1/20+1/2x1/20=3/40
より1x1/40+2x1/40+----+10x1/40+11x3/40+12x3/40+----+20x3/40=13
よって、
1回目13〜20なら終わり 1〜12なら2回目を振る。
2回目、11〜20なら終わり 1〜10なら3回目を振る。
(1回目13の時も、2回目を振ってもよい)
問題5 上記の方針で3回振れる時の得点の期待値を求める
1〜10の確率はそれぞれ、12/20x10/20x1/20=3/200
11,12の確率はそれぞれ、12/20x1/20+12/20x10/20x1/20=9/200
13〜20の確率はそれぞれ1/20+12/20x1/20+12/20x10/20x1/20=19/200
よって期待値は
1x3/200+----+10x3/200+11x9/200+12x9/200+13x19/200+---+20x19/200=14.4
よって4回目まで振れる時の方針は
1回目15〜20なら終わり1〜14なら2回目を振る。
2回目13〜20なら終わり1〜12なら3回目を振る
3回目11〜20なら終わり1〜10なら4回目を振る。
この方針で4回目まで振れる時の期待値は
1〜10の確率はそれぞれ14/20x12/20x10/20x1/20=21/2000
11,12の確率はそれぞれ14/20x12/20x1/20+14/20x12/20x10/20x1/20=63/2000
13,14の確率はそれぞれ
14/20x1/20+14/20x12/20x1/20+14/20x12/20x10/20x1/20=133/2000
15〜20の確率はそれぞれ
1/20+14/20x1/20+14/20x12/20x1/20+14/20x12/20x10/20x1/20=233/2000
よって期待値は
(1+2+------10)x21/2000+(11+12)x63/2000+(13+14)x133/2000+(15+---+20)x233/2000
=15.33
4回目までですでに期待値が15を超えましたので、掛け金1500円なら得だとい
うことになりますが、
5回目まで振れる場合の方針は
1回目16〜20なら終わり1〜15なら2回目を振る。
2回目15〜20なら終わり1〜14なら3回目を振る。
3回目13〜20なら終わり1〜12なら4回目を振る
4回目11〜20なら終わり1〜10なら5回目を振る。
となりこの時の期待値も同様に求めますと
1〜10の確率はそれぞれ15/20x14/20x12/20x10/20x1/20=63/8000
11,12の確率はそれぞ
れ15/20x14/20x12/20x1/20+15/20x14/20x12/20x10/20x1/20=189/8000
13,14の確率はそれぞれ
15/20x14/20x1/20+15/20x14/20x12/20x1/20+15x2014/20x12/20x10/20x1/20=399/8000
15の確率は
15/20x1/20+15/20x14/20x1/20+15/20x14/20x12/20x1/20+15/20x14/20x12/20x10/20x1
/20
=699/8000
16〜20の確率はそれぞれ
1/20+15/20x1/20+15/20x14/20x1/20+15/20x14/20x12/20x1/20+15/20x14/20x12/20x10
/20x1/20
=1099/8000
よって期待値は
(1+--+10)x63/8000+(11+12)x189/8000+(13+14)x399/8000+15x699/8000+(16+--+20)x1
099/8000
=15.9975
実際の世の中では、期待値で考えて得になるような賭け事は存在しませんよね。
そんなこと分かっていても、運試しに賭けをする人がいるわけですが、個人的にはやっぱり世の中うまい話はないので、地道が一番と思っています。
NO4「πP」
8/13 09時32分受信 更新8/20
出た目の期待値で決定すればよいと思います
つまり(1)は出た目と2回目に振りなおす時の期待値の大小関係を考えます
1回目の値はいくつかわかっていますから2度目は期待値でしか表せないとかそんなかんじです
2度目の期待値は(1+2+3+4+5+6)×1/6=21/6=3.5であるから3以下なら振りなおすほうが得であり4以上であればそのまま それがこの問題全てに関係するところですか
「πP」 8/14 00時05分受信 更新8/20
(1)より3以下は振りなおし4以上ならそのままであるから
振りなおしたあとの期待値=一度目の期待値より大きい(つまり4.5.6.がでる場合)と一度目にすでに3.5以上でた場合です(なぜ3以上にしないかというとせっかく(1)で出したのですしこっちのほうが正確ですから
(出題者の意図するところ?)
3.5×1/2+(4+5+6)×1/6=1.75+2.5=4.25になります
よって2回目振りなおしたあとの期待値というのは4.25になります
したがって3回目をするかどうかは4.25以上つまり5または6の出た場合はそのままで1・2・3・4が出た時は振りなおすということになります
で、掛け金400円払ってとくかどうかですが3回目振りなおしたあとの期待値×100と考えられますから
3回目までの期待値の総和=2回目まで振ったときの期待値+3回目に5または6のでる期待値ですから
4.25×2/3+(5+6)×1/6>2.8+1.8=4.6となります
したがって400円払ってこのゲームをするなら得といえます
NO5「kashiwagi」8/14 08時20分受信
更新8/20
176回問題
問1.一つのさいころを振って出る数の期待値は![]()
因って、3以下なら2回目を振り、4以上なら振らない。
問2.上記条件でのもらえる点の期待値は![]() であるから、
であるから、
1回目が4以下なら2回目を振り、5以上なら振らない。又、2回目は問1.より3以下なら3回目を振り、4以上なら振らない。
この場合のもらえる点の期待値は![]()
以上の事から2回まで振れる場合は400円払って425円戻りが期待できる
3回まで振れる場合は466円期待できるから挑戦する価値がある。
問3.普通のさいころの場合と全く同様に![]()
因って、10以下なら2回目を振り、11以上なら振らない。
問4.問2.と同様な計算よりもらえる点の期待値は13となる。
因って、1回目が13以下なら2回目を振り、14以上なら振らない。又、2回目は10以下なら3回目を振り、11以上なら振らない。
問5.もらえる点の期待値は13.7となる。更に計算を重ね、以下の結論を得る。
1回目:15以下なら再度振り、16以上なら振らない。もらえる点の期待値は139
2回目:14以下なら再度振り、15以上なら振らない。もらえる点の期待値は14.4
3回目:13以下なら再度振り、14以上なら振らない。もらえる点の期待値は15.3
4回目:10以下なら再度振り、11以上なら振らない。もらえる点の期待値は15.9
以上より
5回振る場合は1500円払い1590円戻りが期待できる。4回振る場合も1530円期待できる。その他の2,3回振れる場合は1500円未満である。即ち、4回以上振れるなら挑戦する。
NO6「kasama」 8/18 11時11分受信 更新8/20
<コメント:今回も面白い問題ですね。ゲームの引き際はどの時点か計算式で表現できるのでしょうけど、よくわからなかったので、ゲームのツリーを描いて期待値を求めて考察しました。
もっといいやり方があると思いますが、皆様の解答をみて勉強させてもらいます。>
【考え方】
正6面体のサイコロを振って、
1回目に5,6が出たら止める。
2回目に4,5,6が出たら止める。
という方法でゲームをする場合、各々のケースをツリーで表現すると、
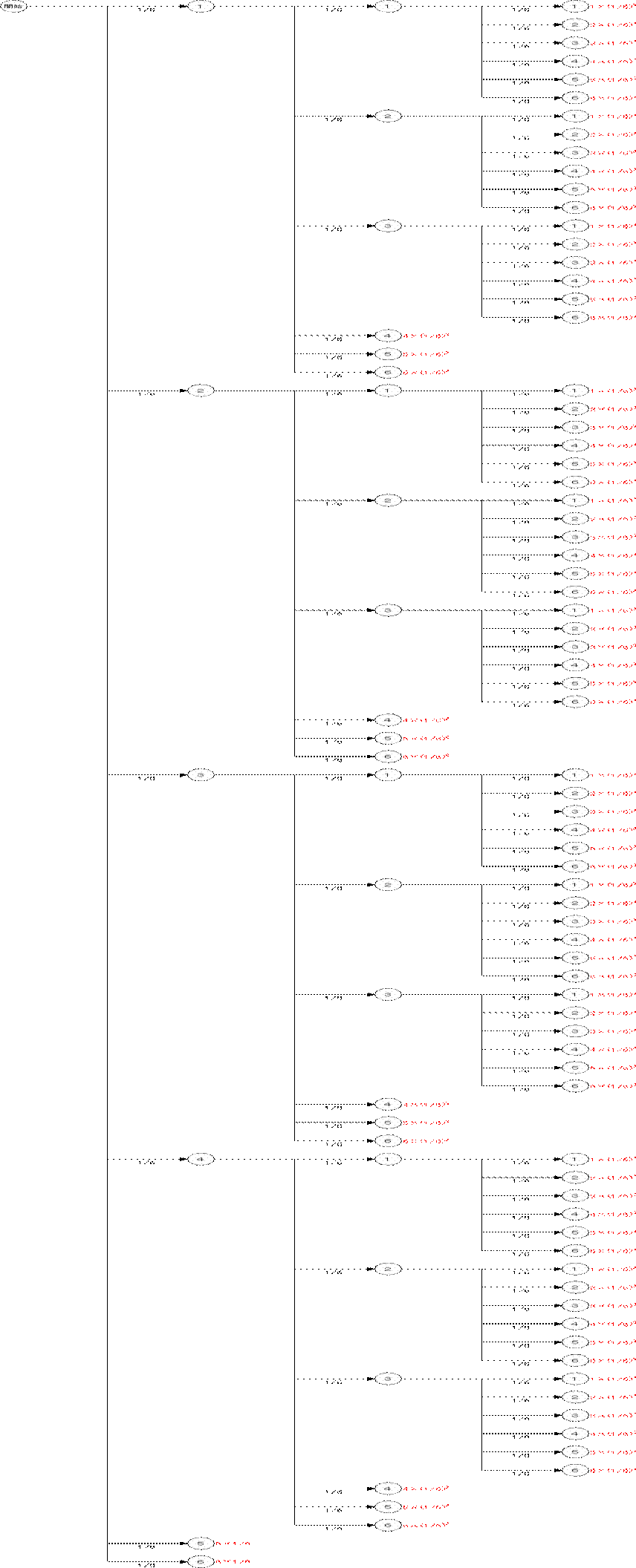
となります。このツリーの期待値は、赤字の個所をすべて加算して、
(5+6)×1/6 + (4+5+6)×(1/6)2×4 + (1+2+3+4+5+6)×(1/6)3×4×3 = 11/6 + 5/3 + 7/6 =
14/3
となります。ゲームを有利に進めるには、この期待値が最大になるようなツリーを見つけ出せば良いのです。
期待値を最大にするツリーの一般的な見つけ方はわかりませんが、ある程度範囲を絞って素手で最適解を見つけるとよいと思います。ただ、素手でやるのは手間なので、プログラムにやらせた方がいいでしょう。下記にその結果を示します。
|
面数 |
振る回数 |
止める数・・・この数字以上なら止める |
期待値 |
||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
6 |
2 |
4 |
- |
- |
- |
- |
17/4 |
|
3 |
5 |
4 |
- |
- |
- |
14/3 |
|
|
4 |
5 |
5 |
4 |
- |
- |
89/18 |
|
|
5 |
5 |
5 |
5 |
4 |
- |
277/54 |
|
|
6 |
6 |
5 |
5 |
5 |
4 |
1709/324 |
|
|
20 |
2 |
11 |
- |
- |
- |
- |
13 |
|
3 |
13 |
11 |
- |
- |
- |
72/5 |
|
|
4 |
15 |
13 |
11 |
- |
- |
1533/100 |
|
|
5 |
16 |
15 |
13 |
11 |
- |
6399/400 |
|
|
6 |
16 |
16 |
15 |
13 |
11 |
26397/1600 |
|
参考までにプログラムを載せておきます
Dai176(m, n)=
{
emax = -9999999;
Dai176Sub(m, 1, vector(n));
print(vmax, ": ", emax);
}
Dai176Sub(m, n, v)=
{
local(i, e);
if (n <= length(v),
for (i=1, m,
v[n] = i; Dai176Sub(m, n+1, v));
,
e = CaliculateExpectation(m,
1, 1, v);
if (e > emax,
vmax = v; emax = e);
);
}
CaliculateExpectation(m, n, k, v)=
{
local(i, s);
s = 0;
if (n <= length(v),
for (i=v[n], m,
s += 1/m*k*i);
s += CaliculateExpectation(m,
n+1, k*(v[n]-1)/m, v);
,
for (i=1, m, s
+= 1/m*k*i);
);
s;
}
【問題1】
1回目に4,5,6が出たら止める。
【問題2】
1回目に5,6が出たら止める。
2回目に4,5,6が出たら止める。
掛け金400円で100倍のお金がもらえる場合、1回の挑戦の期待値は負(-50)なので、損だと思われます。
【問題3】
1回目に11〜20が出たら止める。
【問題4】
1回目に13〜20が出たら止める。
2回目に11〜20が出たら止める。
【問題5】
1回目に16〜20が出たら止める。
2回目に15〜20が出たら止める。
3回目に13〜20が出たら止める。
4回目に11〜20が出たら止める。
掛け金1500円で100倍のお金がもらえる場合、1回の挑戦の期待値は負(-450)なので、損だと思われます。
皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。
![]()
