�����P�W�N�X���R�O��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��1�V�W�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�X���P�O���`�X���R�O��
�m���S����n
�F����A���퐶���̏o�����Ŋ��S����Ƃ����l�����͂悭����܂��B
�@
�P���炎�܂ł̔ԍ��̂��Ă��锠�Ƌ��������āA�P�̔��ɂP�̋������Ă����܂��B
���̔ԍ��Ƌ��̔ԍ������ׂĈقȂ��悤���ꍇ�̐�������o�����p�Ƃ���Ƃ��A���̖�ɓ�����B
�����̗���F��̐̂悤�ɂP�O���ߌ�X���������܂����B��
�����w�E�������uuchinyan�v����ɍő�̊��ӂ����܂��B���肪�Ƃ��������܂����B��
��P�F����o�����p�̏��������S���܂ŋ��߂Ă��������B
��Q�F�����@��n�@�C�����\�P�@�C�@�@�����\�Q�@��p���ĊW�������߂Ă��������B
��R�F����o�����\�������\�P�p�̈�ʍ������ŋ��߂Ă��������B
��S�F���̔ԍ��Ƌ��̔ԍ������ׂĈقȂ�m����Pn�Ƃ���B
�������̂Ƃ��APn�̋Ɍ��l���߂Ă��������B
�m�n�P�uuchinyan�v9/10�@14��19����M �X�V9/30
��P�V�W�w�I�ȉ�����
�m���S����n
9/10 14:00 ���_�ł̖��́A�������������悤�ł��B
���P���炎�܂ł̔ԍ��̂��Ă��锠�Ƌ��������āA�P�̔��ɂP�̋������Ă����܂��B
�����̔ԍ��Ƌ��̔ԍ������ׂĈقȂ鋅�̌��𐔗�o�����p�Ƃ���Ƃ��A���̖�ɓ�����B
�u���̔ԍ��Ƌ��̔ԍ������ׂĈقȂ鋅�̌��v�́A�u���ׂāv����������� a(n) = n �ł��B
�����łȂ��ꍇ�ɂ́A0 <= k <= n �Ƃ��� a(n) = k �ł悭�A���肵�܂���B
������ɂ���A��ӂ��s���m�ŁA���Ƃ��Đ������܂���B
�u���̔ԍ��Ƌ��̔ԍ������ׂĈقȂ�悤�ȏꍇ�̐��v�Ȃ�A�Ӗ����ʂ�܂��B
�����ŁA���̉ł́A
�P���炎�܂ł̔ԍ��̂��Ă��锠�Ƌ��������āA�P�̔��ɂP�̋������Ă����܂��B
���̔ԍ��Ƌ��̔ԍ������ׂĈقȂ�悤�ȏꍇ�̐��𐔗�o�����p�Ƃ���Ƃ��A���̖�ɓ�����B
���Ǝv���āA�ȉ��������܂��B
�����̗���F�쐬�̈Ӑ}�͖��S�������āAe���o�Ă��邱�Ƃ�m���Ă��炤�̂��˂炢�ł����B
�ŁA�����ݖ�`�������Ƃ���ŁA���w�E�̂悤�ȕ��͂ɂȂ�A���l�т��܂��B�܂��A�uuchinyan�v����ɐ[�����ӂ��܂��B��
��P�F
��̓I�ɒ��ׂāA
a(1) = 0, a(2) = 1, a(3) = 2, a(4) = 9
��Q�F
a(n) �́A�� 1 �` n �̔ԍ����� 1 �` n ���ԍ��Ƃ��ׂĈقȂ�ꍇ�ł��B
������������邽�߂ɂ́A�� n �� k �� n �ƂȂ�ԍ��̔��ɓ���Ȃ���Ȃ�܂���B
����́An-1 �ʂ�ł��B���̂Ƃ��A
�c���Ă��鋅�� 1, 2, ..., n-1
�c���Ă��锠�� 1, 2, ..., k-1, k+1, ..., n
�ł��B������A�������בւ��āA
�c���Ă��鋅�� 1, 2, ..., k-1, k+1, ..., n-1, k
�c���Ă��锠�� 1, 2, ..., k-1, k+1, ..., n-1, n
�Ə����Ă݂܂��B��������ƁA�� k ���� n �ɑΉ�����悤�ɂł��܂��B
�����ŁA
a) �� k �� n �ɓ���Ȃ��Ƃ�
b) �� k �� n �ɓ����Ƃ�
�̓�ɕ����čl���邱�Ƃ��ł��܂��B
a) �� k �� n �ɓ���Ȃ��Ƃ�
���̏ꍇ�ɂ́A�ꎞ�I�ɁA���̔ԍ� n �����߂� k �ƐU�蒼���A�ƍl����ƁA
�c���Ă��鋅�� 1, 2, ..., k-1, k+1, ..., n-1, k
�c���Ă��锠�� 1, 2, ..., k-1, k+1, ..., n-1, k(���� n)
�ƂȂ��āA�� 1 �` n-1�A�� 1 �` n-1 �̏ꍇ�ɋA�����܂��B����́A��`��� a(n-1) �ʂ�ł��B
b) �� k �� n �ɓ����Ƃ�
���̏ꍇ�ɂ́A
�c���Ă��鋅�� 1, 2, ..., k-1, k+1, ..., n-1
�c���Ă��锠�� 1, 2, ..., k-1, k+1, ..., n-1
�ƂȂ��āA�ꎞ�I�ɁAk+1 �ȍ~�̔ԍ�������Ȃ��U�蒼���ƍl����ƁA
�� 1 �` n-2�A�� 1 �` n-2 �̏ꍇ�ɋA�����܂��B����́A��`��� a(n-2) �ʂ�ł��B
�ȏ�ł��ׂĂł��B���������āA
a(n) = (n-1) * (a(n-1) + a(n-2))
�ɂȂ�܂��B
��R�F
a(n) = (n-1) * (a(n-1) + a(n-2))
a(1) = 0, a(2) = 1
�����������ł��B�ŏ��̎���ό`���āA
a(n) - n * a(n-1) = (-1) * (a(n-1) - (n-1) * a(n-2))
a(n) - n * a(n-1) = (-1)^(n-2) * (a(2) - 2 * a(1)) = (-1)^(n-2) = (-1)^n
�܂�A
a(n) - n * a(n-1) = (-1)^n
��S�F
���̔ԍ��Ƌ��̔ԍ��̂��ׂĂ̏���̏ꍇ�̐��� n! �ł��B�����ŁA
P(n) = a(n)/n!, P(1) = 0
�ł��B��R�F����
a(n) - n * a(n-1) = (-1)^n
�Ȃ̂ŁA
a(n)/n! - n * a(n-1)/n! = (-1)^n * 1/n!
a(n)/n! - a(n-1)/(n-1)! = (-1)^n * 1/n!
P(n) - P(n-1) = (-1)^n * 1/n!
P(n) = P(1) + ��[k=2,n]{(-1)^k * 1/k!}
P(n) = ��[k=2,n]{(-1)^k * 1/k!} = ��[k=0,n]{(-1)^k * 1/k!}
�Ō�̂Ƃ���́A(-1)^0 * 1/0! + (-1)^1 * 1/1! = 0 ���g���Ă��܂��B
������̓I�ɏ����ƁA
P(n) = (-1)^0 * 1/0! + (-1)^1 * 1/1! + (-1)^2 * 1/2! + ... + (-1)^n * 1/n!
�����ŁA�V����I�ł����A�E�ӂ́A���� e^x �̃}�N���[�����W�J
e^x = 1 + x/1! + x^2/2! + ... + x^n/n!
+ ...
�̒� n ���܂łɂȂ��Ă��܂��B�ؖ��͏ȗ����܂����A�����A���̖��̎�|�ł��Ȃ��ł��傤�A
e^x �̓W�J���͂��ׂĂ̎����Ŏ������邱�Ƃ��m���Ă���A
e^(-1) = 1 + (-1)/1! + (-1)^2/2! + ... + (-1)^n/n! + ...
�ƂȂ�܂��B���̎��̉E�ӂ́Alim[n->��] P(n) �Ȃ̂ŁA���ǁA
lim[n->��] P(n) = e^(-1) = 1/e
�ɂȂ�܂��B
(�l�@)
P(n)�̎����疾�炩�ł����A
a(n) = n! * ��[k=0,n]{(-1)^k * 1/k!} = ��[k=0,n]{(-1)^k * n!/k!}
�Ə����܂��B
����́A��Ⓖ���I�ł����A���̂悤�ɂ��āA���ړI�ɂ����߂��܂��B
�Ȃ��A�ȉ��ł́A�g�ݍ��킹�̐��� C(n,k) �ȂǂƏ����܂��B
�܂��An ����ׂ邷�ׂĂ̏��� n! ����A�� i �ɋ� i
���������ꍇ�A
C(n,1) * (n-1)! �������܂��B
n! - C(n,1) * (n-1)!
�Ƃ��낪����ł́A�� i �ɋ� i ������A�� j �ɋ�
j ���������ꍇ�A
C(n,2) * (n-2)! �������߂��Ă���̂ŁA�����₤���߂ɉ����܂��B
n! - C(n,1) * (n-1)! + C(n.2) * (n-2)!
�Ƃ��낪���x�́A�� i �ɋ� i ������A�� j �ɋ�
j ������A�� k �ɋ� k ���������ꍇ
C(n,3) * (n-3)! �𑫂��߂��Ă���̂ŁA�����₤���߂Ɉ����܂��B
n! - C(n,1) * (n-1)! + C(n.2) * (n-2)! - C(n.3) * (n-3)!
�D�D�D�ȉ����l�ɂ��āA���ǁA
n! - C(n,1) * (n-1)! + C(n.2) * (n-2)! - C(n.3) * (n-3)! + ... + (-1)^n * C(n,n) * 0!
�܂�A
a(n) = ��[k=0,n]{(-1)^k * C(n,k) * (n-k)!}
= ��[k=0,n]{(-1)^k * n!/k!(n-k)! * (n-k)!}
= ��[k=0,n]{(-1)^k * n!/k!}
�ɂȂ�܂��B
���́A�u�����đ����āv�̌J��Ԃ��́A��ʂɁA��̌����Ƃ����炵���̂ł����A
�v����ɁA�a�W���ŗv�f�𐔂���ۂ̌v�Z�A
n(A��B��C) = n(A) + n(B) + n(C) - n(A��B) - n(B��C) - n(A��C) + n(A��B��C)
�̈�ʉ��ł��ˁB
(���z)
�������߂������ĉ����܂����B����ł悩�����̂ł��傤���H
�ꉞ�A��������ŁAWeb�Łu���S����v���������Ă݂��Ƃ���A���̉��߂̂��̂��o�Ă����̂ŁA
�����Ǝv���̂ł����D�D�D
�Ȃ��A�u���S����v�́A�u�����g�[�����v�A�u������(����)����v�ȂǂƂ������悤�ł��ˁB
�����̗���F�w�Z�̐����ł́u�ȑւ����v�Ƃ��āA�����Ă��܂��B
�������������āA�O��Ɠ����Ȃɒ������k�����Ȃ��Ƃ��P�l�ȏア��m���͂P�|1/e���O�D�U�R�@�i��j���܂��āA���w�I�Ȋm���͘b���Ă݂�ƁA���Ƃ��Ë����Ă���܂��B�܂��A����̒��ł́u�l�ԂƌC�v�A�u�l�ԂƖX�q�v�A�u�莆�ƈ��������v�A�u�p�[�e�C�̂Ƃ��̂��݂��ɍs���v���[���g�����v
�u�e�X�g�̂Ƃ��{�b�N�X�ɈقȂ鐔�����P�����Ă͂߂���v�����k�ɂ͘b���Ă��܂��B��
�m�n�Q�u��P�v�@ 9/10�@16��34����M �X�V9/30
��P�F������n=1�̎��H0
��2����n=2�̎�1
�@�@�@��3����n=3�̎�2
�@�@�@��4����n=4�̎�9
�S�Ď��`�}�ŏ����܂����@�����Ɛ��������Ƃ܂��͍ŏ����P�łȂ����̂�S�ĕ��ׂĂ�������2�Ԗڂ�2�@�O�Ԗڂ�3�E�E�E�ł�����̂������悢�̂ł����E�E�E�@�������Ȃ����́i���ɉ���ɂ������̂́j��͂���`�}�ł���
��2�F�ǂ�������ɂ����@�ł�����Ƃ肠�������`�}��`���čl���Č��܂�
�@�������g����n=3�̎����l���Č��܂��@����ƈȉ��̂悤�ɂȂ�܂�
�Q�|�R�|�P
�R�|�P�|�Q
���̂Q�ʂ肾���ƂȂ�܂��@�@�@���Ă��ꂩ����邱�Ƃ́E�E�E
�܂��͍ŏ��͂P�łȂ�����ŏ��̐��̂Ƃ����3-1=2�ʂ�
�܂��Ō�̐��͍ŏ��̐������܂�킩��̂ōŌ�̐��̎�����1�ʂ�
����čl����̂͊Ԃ̐��̊��S����ƂȂ�܂����猋�ǂ́i3-1�j�~�iA3-2�j�@�ƂȂ�͂��E�E�E�ł������I�ǂ���������s�K�ɂȂ�悤�ł�
�ł����牽���������Ă�Ƃ������ƂɂȂ�܂��@��蕶��苰�炭�����A3-1�Ȃ̂ł��傤�@�����ɑ����Ă݂�Ɓi3-1�j�~�iA3-1+A3-2�j���Q�ƂȂ�܂����炱�ꂪ�����ƂȂ�K���ł���܂�
����������ł͐��w�I�ȉ������͈���Ă܂���I�@����͍���I��@�ł�
�ł͐��𑝂₵��n=4�̎����l���Č��܂�
2-1-4-3 3-1-4-2 4-1-2-3
-3-4-1 -4-1-2
-4-1-3
2-1 -2-1
����ʼn���悤�ɂǂ���犮�S����ɂ̓p�^�[����������āE�E�E
�i�@�j�@�ŏ�����Ō�܂łŕ������̂���Ԗڂ̎�
�@�@�@�@�@�@����͈�̂������邩�Ƃ����܂��ƁE�E�E�@
�@�@�@�@�@�ŏ��̐��͉��ʂ肠�邩�͕s���@�������ŏ������܂�Ō������̐��i���Ȃ킿���̏ꍇ��4�j�͏�����܂����猋�ǂ��̏ꍇ�̊��S����̌��͒��ۓI�ɂȂ�܂����E�E�EAn-2�ʂ�@�i���̗�̈�Ƃ��čŏ���2�̏���ƍŏ���3�̏����4�|�̏ꍇ�����������̂ƍŏ���4��3-�̏ꍇ�����������̂ōŏ��ƍŌ���������ꍇ�̂��ƂɂȂ�܂��E�E�E�^�u���j
�i�A�j�ŏ�����Ō�̒��œr���̕����������ԖڂłȂ�����
�@�@����̐��͂Ƃ����ƁE�E�E
�@�@�Ƃ肠�����͕������Ƃ������ԖڂƂ��܂��Ă��̊��S����̌��Ƃ����̂͌��ǂ͍ŏ��̐���������An-1�̊��S����ł���܂�
�@�@���̗�ł�3��������3�̊��S����Ƃ����܂���
���āE�E�E�����݂͌��ɔw���ł�����a�̖@����芮�S����̌��Ƃ����̂͌��ǁ@A����An-2+A��-1
�ł͂Ȃ��āE�E�E����ɍŏ��̐��̑I�ѕ����|�����@An��(n-1)�~�iAn-1+An-2)
���ꂪ�������ȁ@�@�@���̌`�͂ǂ����ŏ��̐����킩��ǂ�ǂ�킩���Ă����Ƃ������̂̂悤�ł���
�ꉞ���Z�����Ă����ƁE�E�E
A4���i4-1�j�~�iA4-1+A4-2�j
�@�@���R�~�iA3��2+A2��1�j
�@�@���X
�ƂȂ�K�@���ꂾ���ł͂܂��s�\���i������g���Đ��_���Ă�������j A5���S�~�i�X+�Q�j��44
�ꉞ���`�}���`���Ċm���߂܂�������ȏ�͔��܂������R�@�S�@�T�@�̏ꍇ���K���Ȃ̂����瑼�������ƁE�E�E
�����̗���F�u��P�v����̉������́A�ŏ��A�A�[�I�ɒ��ׂāA��������A�K���������Ă����l�����ł��B�܂��A���`�}�������Ď��ۂɊm���߂Ă��܂��B���w�I�ȍl���̊�{�ł��B��
�m�n�R�uToru�v�@
9/12�@15��16����M �X�V9/30
��P�@a1=0,
a2=1, a3=2 (231,312)
�@�@ ,a4=9 (2143,2341,2413,3142,3412,3421,4123,4312,4321)
��Q�@��n�ɂ͂����Ă��鋅��k�@�ik��1,2,---,n-1�̂����ꂩ�j�Ƃ���B
�@��n ����k�ɂ͂����Ă���ꍇ�̐��́A1,2,--,k-1,k+1,--n-1�@��n-2�����S����
�̏ꍇ�̐���a(n-2)
�@��n����k�ȊO�ɓ����Ă���ꍇ�̐��́A��n����k�Ǝv���A1,2,----,n-1��n-1��
�̊��S����ꍇ�̐��Ł@a(n-1)
�@k=1,2,----,n-1�̂�����ł����l�ł��邩��
�@an=(n-1)(a(n-1)+a(n-2))
��R�@��Q�̑Q������ό`���āA
�@an-n a(n-1)=-(a(n-1)-(n-1) a(n-2))=--
-=(-1)^(n-2) (a2-2a1)=(-1)^(n-2)=(-1)^n
��S�@��R�̗��ӂ�n!�Ŋ�����
Pn-P(n-1) =(-1)^n/n! , P1=0�Ƃ���@n=2,3,4,----,n�Ƃ��ĕӕӂ�������
Pn=1/2!-1/3!+1/4!-1/5!+------+(-1)^n/n!
n�����Ƃ���Ƃ����e^x�̃e�[���[�W�J
e^x=1+x+x^2/2!+x^3/3!+--------
�ɂ�����x=-1�Ƃ������̂Ɉ�v���邩��@n�����@�̎��@Pn��1/e
��P�V�W����̉𑗂�܂��B�Ȃ��Ȃ����������ł��ˁB���ɖ�S�͉�������
�ŃX�J�b�Ƃ��܂��B�@�@�@
�����̗���F�uToru�v����̉�@�́A�Y��ŗD�낳�������܂��B��������A���z�Ɂu������[�v�Ƃ����[�������\��Ă��܂��B��
�m�n�S�ukashiwagi�9/12�@21��33����M �X�V9/30
178����
��1.�������o���Ă݂�ƁA![]()
![]()
![]()
![]()
![]() �ƂȂ邱�Ƃ�������B
�ƂȂ邱�Ƃ�������B
��2.��̒l��莎�s����̌��ʁA![]() �ƂȂ邱�Ƃ�������B
�ƂȂ邱�Ƃ�������B
��3.��L����ό`����ƁA
![]()
�@�@�@�@�@�@�@��![]()
![]()
�@�@�@�@�@�@�@��![]() �@�@�ƂȂ�B
�@�@�ƂȂ�B
��4.![]() �I�ł��邩��A��L����
�I�ł��邩��A��L����![]() �I�Ŋ����đS�Ă̍���������ƁA
�I�Ŋ����đS�Ă̍���������ƁA
�@�@�@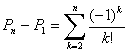 �@�ƂȂ�B������
�@�ƂȂ�B������![]() �@�A1�I���O�I��1�ł��邩��
�@�A1�I���O�I��1�ł��邩��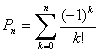 �@�@�@�@�����A
�@�@�@�@�����A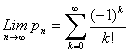 ��
��
�@�@�@![]()
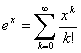 �@�ł��邩��@
�@�ł��邩��@![]() �@�ƂȂ�B
�@�ƂȂ�B
���������g�F����̖��͔��ɖʔ����ł��ˁB��ӂɉ����Čv�Z���� �����Ɖ��Ǝ��R�ΐ���e���łĂ���Ƃ́A�������Ȃ���{���ɓ��̗ǂ��l����������ł��ˁB�}�l�ɂ͔��z���ł��܂���E�E�E�E��
�����̗���F��@�̑�햡�𖡂키���Ƃ��ł��܂������B���h�Ɋ����܂��B�Ƃɂ����Ae�@���łĂ��܂�����ˁB
�@�������肵���������ȉ�@�ł��B��
�m�n�T�u�O�p��K�9/18�@21���S�Q����M
�X�V9/30
���R�����g�F����� �u�������[���̖��v �́C�Y�꓾�ʎv���o������܂��B
���߂Ă̏o��́C�����g�����Z3�N�̂Ƃ��C�w��w�ւ̐��w�x �̒��̒|�V���������̋L���ɂ����Ăł����B
�����ɂ͑Q�����Ɏ����ʘ_�̋L�q�͂���܂���ł������C���̐_��I�Ȗ��͂͐[����ۂƂȂ��Ďc��܂����B
��w�̐}���قŗ��U���w�̖{���E���ǂ݂����Ƃ��C���R�������Q�����Ƃ��̉�������ɐ[����ۂɍ��܂�܂����B
���̏ڍׂ܂Ŋo���Ă�����͂��������͂���܂��C�{��͂��̒��̂ЂƂł��B�v
�����̗���F����͎v���o�[�����̂悤�ł��āA���h�Ɋ����܂��B
���̏ꍇ�͋��������U�N�ڂł��āA�S���Ⴂ�ꍇ�̐����Q�����ŕ\����邱�Ƃ�
���k�ɐ������Ȃ���A�������[�����Ƃ��ė��j�I�ɗL���Ȃ��Ƃ�b���Ă��܂����B��

�m�n�U�ukasama��@����@9/30�@00��36����M �X�V9/30
���R�����g�F����͊��S����̖��ł��ˁB�ݖ�ʂ�ɂ���Ă����ƁA���܂��m���ɒH�蒅���܂����A�Ɍ��l���O�ł͂Ȃ��A����l(1/e)�Ɏ�������Ƃ��낪�����[���ł��ˁB��
��P
a1 0�ʂ�
a2 (2,1) 1�ʂ�
a3 (2,3,1),(3,1,2) 2�ʂ�
a4
(2,1,4,3),(2,3,4,1),(2,4,1,3),(3,1,2,4),(3,4,1,2),(3,4,2,1),(4,1,2,3),(4,3,1,2),(4,3,2,1)
9�ʂ�
��Q
n�Ԗڂ̕�����1�`n-1��n-1�ʂ�ł��B�����ŁAn�Ԗڂ�i��u�������̂ɂ��čl���܂��B
�@i�Ԗڂ�n����ׂ��ꍇ
�@i�Ԗڂ�n�An�Ԗڂ�i������̂�����A�c���n-2���̕��т͊��S����Ȃ̂ŁAan-2�ʂ�ł��B
�Ai�Ԗڂ�n����ׂȂ��ꍇ
�@i�Ԗڂ�n����ׂȂ��̂ŁAn��i�Ɠǂݑւ��Ă��\���܂���B����ƁA1�`n-1�Ԗڂ̕��т͊��S����Ȃ̂ŁAan-1�ʂ�ł��B
�@�A�A��n�Ԗڂ̕����̕��ו���n-1�ʂ肠�邱�Ƃ��A
�@an = (n-1)(an-2+an-1) ���(1)
�ƂȂ�܂��B
��R
(1)�������̂悤�ɕό`���܂��B
�@an = (n-1)(an-2+an-1)��an = (n-1)an-2+nan-1-an-1��an-nan-1 = -{an-1-(n-1)an-2}
����ƁA
�@an-nan-1 = (-1)1{an-1-(n-1)an-2} = (-1)2{an-2-(n-2)an-3} = ��� = (-1)n-2(a2-2a1) = (-1)n
����āA
�@an-nan-1 = (-1)n ���(2)
�ł��B
��S
n�̐����̏����n!�ʂ�Ȃ̂ŁAPn
= an/n!�ł��B��R��(2)���𗘗p���邽�߁AP�̍������Ƃ��āA
�@Pn-Pn-1 = (-1)/n�(Pn-1-Pn-2) = (-1)2/n(n-1)�(Pn-1-Pn-2) = ���
�@= (-1)n-2/n(n-1)���3�(P2-P1) = (-1)n-2/n(n-1)���3�(1/2-0) = (-1)n/n!
�ƂȂ�̂ŁA
�@Pn
= (-1)n/n!-Pn-1 = (-1)n/n!+(-1)n-1/(n-1)!-Pn-2 = ���
�@= (-1)n/n!+(-1)n-1/(n-1)!+���+(-1)2/2!-P1 = ![]() {(-1)k/k!} =
{(-1)k/k!} = ![]() {(-1)k/k!}
{(-1)k/k!}
�ƂȂ�܂��B����͎��R�ΐ��̒�ex���n���܂�Taylor�W�J���āAx=-1�����������̂ł�����An�����̂Ƃ�1/e=0.367879����ł��B
![]()
