�����P�X�N�P�O���P�S��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��1�X�V�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�X���Q�R���`�P�O���P�S��
�m�t�[���G�����i�P�j�n
�F����A�[�[�^�[���������m�ł����B����̖��̓t�[���G�����ƃāi�Q�j�̊W�ł��B
�@
NO1�uuchinyan�v09/23 13��22����M �X�V10/14
��P�X�V�w�I�ȉ�����
�m�t�[���G�����i�P�j�n
�܂��́C�ŏ��̎O�p���̒��𐫂��瓱���Ă��܂��܂��傤�B
(1) m, n �� m, n > 0 �Ȃ鐮���Ƃ��܂��B
I = ��[-�`��] sin(mx)sin(nx) dx
= - 1/2 * ��[-�`��] {cos((m+n)x) - cos((m-n)x)}
dx
�����ŁC
�Em not= n �̏ꍇ
I = - 1/2 * [sin((m+n)x)/(m+n)
- sin((m-n)x)/(m-n)][-�`��]
= 0
�Em = n �̏ꍇ
I = - 1/2 * ��[-�`��] {cos(2mx) - 1} dx
= - 1/2 * [sin(2mx)/(2m) - x][-�`��]
= ��
(2) m, n �� m, n >= 0 �Ȃ鐮���Ƃ��܂��B
I = ��[-�`��] cos(mx)cos(nx)
dx
= 1/2 * ��[-�`��] {cos((m+n)x) + cos((m-n)x)}
dx
�����ŁC
�Em not= n �̏ꍇ
I = 1/2 * [sin((m+n)x)/(m+n)
+ sin((m-n)x)/(m-n)][-�`��]
= 0
�Em = n not= 0 �̏ꍇ
I = 1/2 * ��[-�`��] {cos(2mx) + 1} dx
= 1/2 * [sin(2mx)/(2m) + x][-�`��]
= ��
�Em = n = 0 �̏ꍇ
I = 1/2 * ��[-�`��] {1 + 1} dx
= [x][-�`��]
= 2��
(3)
I = ��[-�`��] sin(mx)cos(nx)
dx
sin(mx)cos(nx) �͊���Ȃ̂ŁC���炩�ɁCI = 0 �ł��B
���āC���悢����ł��B
-�� < x < �� �ŁC
x/2 = ��[m=1,��] b(m) * sin(mx)
�Ə����Ă���Ƃ��܂��B�������C�A�������ɂ���悤�ɁC
(A)�@���̖����a���̏��������͉\
(B)�@���̖����a�Ɛϕ��̏��������͉\
�Ɖ��肵�܂��B
���P�F�� ���Q�F
�����̗��ӂ� sin(nx)�Cn = 1, 2, 3, ...�C���|���āCx �� -�`�� �Őϕ�����ƁC
��[-�`��] {x/2 * sin(nx)} dx = ��[-�`��] {��[m=1,��] b(m) * sin(mx)} * sin(nx) dx
�E�� = ��[-�`��] {��[m=1,��] b(m) *
sin(mx)} * sin(nx) dx
= ��[m=1,��] b(m) * ��[-�`��] sin(mx)sin(nx) dx�@<---�@(B)
= b(n) * �@<---�@(1)
���� = ��[-�`��] {x/2 * sin(nx)} dx
= 1/2 * ��[-�`��] {x * sin(nx)} dx
= 1/2 * [- x * cos(nx)/n][-�`��] - 1/2 * ��[-�`��] {-
cos(nx)/n} dx�@<---�@�����ϕ�
= - ��/2n * 2 * (-1)^n - 1/2 * [- sin(nx)/n^2][-�`��]
= �� * (-1)^(n-1)/n
�����ŁC
b(n) = (-1)^(n-1)/n, n = 1, 2, 3, ...
���ɁC
b(1) = 1, b(2) = - 1/2, b(3) = 1/3
���R�F
���P�F�� ���Q�F���C
x/2 = ��[m=1,��] (-1)^(m-1)/m *
sin(mx)
�Ə����܂��B�����ŁC���ӂ��悵�āCx �� -�`��
�Őϕ�����ƁC
(x/2)^2 = (��[m=1,��]
(-1)^(m-1)/m * sin(mx))^2
x^2/4 = (��[m=1,��] (-1)^(m-1)/m
* sin(mx)) * (��[n=1,��] (-1)^(n-1)/n * sin(nx))
x^2/4 = ��[m=1,�� �� n=1,��] {(-1)^(m-1)/m * (-1)^(n-1)/n * sin(mx) *
sin(nx)}�@<---�@(A)
��[-�`��] {x^2/4} dx
�@= ��[-�`��] {��[m=1,�� �� n=1,��] {(-1)^(m-1)/m * (-1)^(n-1)/n * sin(mx) *
sin(nx)}} dx
�E�� = ��[-�`��] {��[m=1,�� �� n=1,��] {(-1)^(m-1)/m * (-1)^(n-1)/n * sin(mx) *
sin(nx)}} dx
= ��[m=1,�� �� n=1,��] {(-1)^(m-1)/m * (-1)^(n-1)/n * ��[-�`��] sin(mx)sin(nx)
dx}�@<---�@(B)
= ��[n=1,��] {(-1)^(n-1)/n *
(-1)^(n-1)/n * ��}�@<---�@(1)
= �� * ��[n=1,��] 1/n^2
���� = ��[-�`��] {x^2/4} dx
= [x^3/12][-�`��]
= ��^3/6
�����ŁC
��[n=1,��] 1/n^2 = ��^2/6
�ɂȂ�܂��B
(���z)
��[n=1,��] 1/n^2 = ��(2) �ł��ˁB�ȒP�ɏؖ��ł��Ă��܂��̂ɂ͋����ł����B
�܂��C(A)�͖����a����Ύ�������Ƃ��ɁC(B)�͖����a����l��������Ƃ��ɐ������C
�t�[���G�����ł͂���炪������C�̂ł����B
��w�̎��ƂŏK���܂������C�ؖ��܂ł͖Y��Ă��܂��܂����B���Ԃ������ĕ��K���Ă����܂��B
�Ȃ��C�m�t�[���G�����i�P�j�n�Ƃ���̂ŁC����ӂ�́C�m�t�[���G�����i�Q�j�n�H
����ɁA�C��(2)���ȒP�ɋ��܂��Ă��܂��̂ɂ͋����ł����B��
NO2�ubear56�v�@09/23 21��17����M
NO2�ubear56�v�@09/24 13��44����M
NO2�ubear56�v
09/24 17��00����M �X�V10/14
���R�����g�F�t�[���G�����i�P�j�ɂ��āD����l����K�v�͖��������悤�ł��D
����Ă݂���o���܂����D����́C�e�L�X�g���������ł̕\���������̂ŁC
LaTeX���g���āCPDF�o�͂��܂����D�\�[�X�Ƌ��ɓY�t�v���܂��D��

\documentclass[a4paper,fleqn]{jsarticle}
\usepackage{amsmath,amssymb}
\usepackage{type1cm}
\usepackage{txfonts}
\usepackage{euler}
\usepackage[T1]{fontenc}
\usepackage{textcomp}
\pagestyle{empty}
\begin{document}
�܂��C$f(x)=x$�Ƃ��ăt�[���G�����W�J����D
�t�[���G�W���̌�������C
![]() \begin{equation}
\begin{equation}
a_0 = \frac{1}{\pi} \int_{-\pi}^{\pi}
f(x) \ dx
\end{equation}
\begin{equation}
a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} \cos nx \ f(x) \ dx \quad (n = 1, 2,
3, \dots)
\end{equation}
\begin{equation}
b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} \sin nx \ f(x) \
dx \quad (n = 1, 2, 3, \dots)
\end{equation}
�����ŁC$f(x)=x$�͊���̂��߁C$a_n$�̍��͏����C$b_n$�̍����c��C
\begin{gather*}
a_0 = a_1 = a_2 = a_3 = \dots = 0 \\
b_1 = \frac{1}{\pi} \int_{-\pi}^{\pi}
x \sin x \ dx = 2, \
b_2 = \frac{1}{\pi} \int_{-\pi}^{\pi}
x \sin 2x \ dx = -1, \
b_3 = \frac{1}{\pi} \int_{-\pi}^{\pi}
x \sin 3x \ dx = \frac{2}{3},
\
\dots .
\end{gather*}
���������āC
\begin{gather}
f(x) = x = 2 \left( \sin x - \frac{1}{2} \sin 2x + \frac{1}{3} \sin 3x + \dots \right) \\
\frac{x}{2} = \sin x - \frac{1}{2}
\sin 2x + \frac{1}{3} \sin 3x + \dots \label{eq:fsx}
\end{gather}
����ɁC\eqref{eq:fsx}�̗��ӂ�2�悵�āC$-\pi$ ���� $\pi$ �܂Őϕ�����ƁC
\begin{equation}
\int_{-\pi}^{\pi} \frac{x^2}{2^2}\
dx
= \int_{-\pi}^{\pi} \left( \sin x - \frac{1}{2} \sin 2x + \frac{1}{3}
\sin 3x + \dots \right)^2 dx \label{eq:square}
\end{equation}
�����ŁC\eqref{eq:square}�̉E�ӂ�W�J���C���ʂɐϕ�����ƁC����\eqref{eq:sinmxsinnx}�ɂ��C2��̍��ȊO�͏��������D
\begin{equation}
\text{$m$�C$n$�𐳂̐����Ƃ���Ƃ��C} \quad
\int_{-\pi}^{\pi} \sin mx \
\sin nx \ dx =
\begin{cases}
0 & (m \neq n) \\
\pi & (m = n)
\end{cases} \label{eq:sinmxsinnx}
\end{equation}
���������āC
\begin{align}
\int_{-\pi}^{\pi}\frac{x^2}{2^2}\
dx &= \pi + \frac{\pi}{2^2}
+ \frac{\pi}{3^2} + \dots \\
\frac{1}{4} \left[ \frac{1}{3}
x^3 \right]_{-\pi}^{\pi} &= \pi \left( 1 + \frac{1}{2^2}
+ \frac{1}{3^2} + \dots \right) \\
\frac{1}{12} \left[ \pi^3 - \left( -\pi^3 \right)
\right] &= \pi \sum_{n=1}^{\infty} \frac{1}{n^2} \\
\frac{\pi^2}{6} &= \sum_{n=1}^{\infty} \frac{1}{n^2}.
\end{align}
����āC
\begin{enumerate}
\item[���1] : $\displaystyle
b_1 = 1, \ b_2 = -\frac{1}{2}, \ b_3 = \frac{1}{3}.$
\item[���2] : $\displaystyle b_n = (-1)^{n-1}\frac{1}{n}.$
\item[���3] : $\displaystyle
\sum_{n=1}^{\infty} \frac{1}{n^2}
= \frac{\pi^2}{6}.$
\end{enumerate}
\end{document}
NO3�u���[��v09/27 13��39����M �X�V10/14
���P
�@���̗��ӂ�sin
x�Csin
2x�Csin
3x�������C���ꂼ��]p����p�܂Őϕ�����ƁC
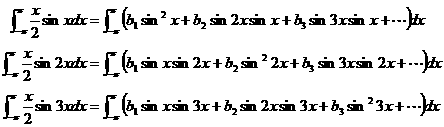
�E�ӂɌ���(1)��K�p����Ƃ��ꂼ��Q��̍������̂���C
![]() �ƂȂ�D����āC
�ƂȂ�D����āC![]() �D
�D
���Q
���l�ɇ@���̗��ӂ�sin
nx�������]p����p�܂Őϕ����Đ�������ƁC
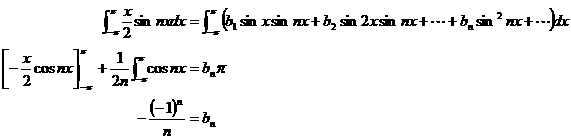
���R
�@�������������ƁC![]() �D
�D
������Q�悵�Đϕ�����ƁC
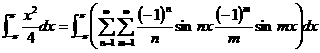 �D
�D
����(1)���E�ӂ�n��m�̍��͏����ĂQ��̍������̂���C![]() �ƂȂ�D
�ƂȂ�D
���������āC![]() �D
�D
���R�����g�F�����t�ɊÂ��āC�����a�̎������ɂ��Ċ��S�����ł����C�����Ƃ�낤�Ƃ���Ɠ����ł��傤�ˁD
�������킹�Ɍ����W�����܂������C�������ꂪ�C�[�[�^���Ƃ�����Ȃ�ł��ˁI�H��
NO4�uToru�v 09/28 16��48����M �X�V10/14
���P
���ӂ�sin x�������ā@�|�`�܂Őϕ����āA(1)�𗘗p����ƉE�ӂ͑�ꍀ�ȊO��0
�ƂȂ��ꍀ�̓�b1���
�i�E�Ӂj=��b1
�i���Ӂj=�E(�|�`��) x sinx dx =[-
x cos x]+�Ecosx dx=��
����� b1=1
���l��sin 2x �������Đϕ�����Ɓ@
(�E��)=��b2
(����)=[-x cos2x/2]+�Ecos2x/2 dx= -��/2
���b2=-1/2
���l��sin 3x �������Đϕ������
(�E��)=��b3
(����)=[-x cos3x/3]+�Ecos3x/3dx= ��/3
���b3=1/3
���Q�@���P���bn=(-1)^(n-1)/n �ƍl������B
����sin nx�������Đϕ������
(�E��)=��bn
(����)=[-x cosnx/n]+�Ecosnx/n dx= (-cosn��)��/n=(-1)^(n-1) /n
���R
?�̗��ӂ��悷��ƉE�ӂ̊e����(1)�̂悤�Ȍ`�ɂȂ邪�A�����ϕ�����Ίe��
���悵�����̂������c��
(�E��)=��(b1^2+b2^2+b3^2+--------)=��1/n^2
�i���Ӂj=�E(-�`��) (x/2)^2 dx =[x^3/12] -�`��)=��^3 /6
���ꂩ�烰1/ n^2=��^2 / 6
���R�����g�F�@���������̍��ʐϕ����A�ς��A�ؖ��Ȃ��ł悢�Ƃ������Ƃł�������ς�C��
�Ȃ�܂��ˁB�܂������Ă݂悤�Ǝv���܂��B
�@zeta(2)�̘a�ɂ��ẮAf(x)=x^2�i0��x���j���t�[���G�W�J���āAx=�ƒu��
���@���{�Ō����o��������܂��B��
�@�@�@�@�@�@�@�@�@�@�@�@�@
NO5�u�V�o�l�����v10/2 17��41����M �X�V10/14
���R�����g�F��P�X�V����ł����A���P���番����܂���ł����B���l��������낢����������ł����A���P������������ό`���v���t���܂���ł����B�����ŁA�t�[���G�����̌��莖���������o���A�t�ɖ��P���l���Ă��܂��܂����B���Q�̐ݒ�i�����j�ɂ�肱��́A�Ⴄ�Ǝv���Ȃ���̉ł��B��

NO�U�ukasama�v
10/11 01��42����M �X�V10/14
�@���R�����g�F����̓t�[���G�����̖��ł��ˁB�t�[���G�����͊w������ɃX�y�N�g����͂ŏK�����o��������܂����A�قƂ�ǖY��Ă��܂����B�̂̃e�L�X�g�����Ȃ�����܂����B
�����a�Ɛϕ��̌����͊m�������a����l�������邱�Ƃ������������C�����܂����悭�o���Ă��܂���B
|
���P�@�����t�[���G�W�������߂�ƁA���̂悤�ɂȂ�܂��B |
|
���Q�@�O����A(-1)n+1/n�Ɛ����ł��܂��B���ۂɂ���Ă݂�ƁA���̂悤�ɂȂ�܂��B |
|
���R�@��ӂɂ���@���Q�悷��ƁA |
NO7�ukashiwagi�10/11 09��01����M �X�V10/14
���R�����g�F���E�̑�D���ł� �����t�[���G�����̖��ŁA�w��������������݂Ȃ���������Ē����܂����B ���X�ȗ������ł����E�E�E��
197����
��1.���@�̗��ӂ�![]() ���|���A-�`�܂Őϕ�����B
���|���A-�`�܂Őϕ�����B
![]()
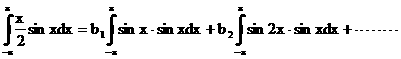
���ӂ͕����ϕ����A�E�ӂ͎O�p���̒��𐫁i1�j��K�p���v�Z����ƁA����![]() �ƂȂ�A
�ƂȂ�A
![]() ��1�ł���B
��1�ł���B
���Ƃ͑S�����l��![]() ���𗼕ӂɊ|���Đϕ����s���ƁA
���𗼕ӂɊ|���Đϕ����s���ƁA![]() �A
�A![]()
��2. �ސ�����![]() �ƂȂ�B
�ƂȂ�B
��3.��L���A
![]() �@�ł��邩��A���ӂ���-�`�܂Őϕ�����B
�@�ł��邩��A���ӂ���-�`�܂Őϕ�����B
![]()
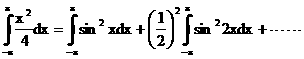
![]() �ł��邩��A
�ł��邩��A
![]() �����߂���̂ł���B
�����߂���̂ł���B
![]()
