平成２０年８月３日

[流れ星]

　　　　　第２１０回数学的な応募問題解答

　　　　　　＜解答募集期間：７月１３日〜８月３日

［相加平均・相乗平均］

皆さん、教科書傍用問題集（数研出版）を見ていたら、相加平均・相乗平均の証明問題がでていました。

一部改題してあります。

NO1「uchinyan」 7/13 11時35分受信 更新8/3

第２１０回数学的な応募問題への解答 を送ります。
新たな相加相乗平均の証明法をご紹介いただきありがとうございました。勉強になりました

第２１０回数学的な応募問題
［相加平均・相乗平均］

問題１：
f(x) = ((x + k)/2)^2/x, x > 0, k > 0
まずは，最小値を求めてみます。
f'(x) = {2 * (x + k)/2 * 1/2 * x - ((x + k)/2)^2 * 1}/x^2
= (x + k)/2 * {x - (x + k)/2}/x^2
= (x + k)/2 * 1/2 * (x - k)/x^2
x > 0, k > 0 においては，
0 < x < k で，f'(x) < 0，f(x) は 単調減少
x = k で，f'(x) = 0，f(x) は 極小かつ最小
k < x で，f'(x) > 0，f(x) は 単調増加
なので，
f(x) >= f(k) = k : 最小値
((x + k)/2)^2/x >= k
となります。ただし，等号は，x = k のときです。
そこで，x = a > 0, k = b > 0 とおくと，
((a + b)/2)^2/a >= b
((a + b)/2)^2 >= ab
a, b は，正の実数なので，
(a + b)/2 >= √(ab)
になります。ただし，等号は，x = k のときなので，a = b のときです。

問題２：
同様にやってみます。
f(x) = ((x + k)/3)^3/x, x > 0, k > 0
f'(x) = {3 * ((x + k)/3)^2 * 1/3 * x - ((x + k)/3)^3 * 1}/x^2
= ((x + k)/3)^2 * {x - (x + k)/3}/x^2
= ((x + k)/3)^2 * 1/3 * (2x - k)/x^2
x > 0, k > 0 においては，
0 < x < k/2 で，f'(x) < 0，f(x) は 単調減少
x = k/2 で，f'(x) = 0，f(x) は 極小かつ最小
k/2 < x で，f'(x) > 0，f(x) は 単調増加
なので，
f(x) >= f(k/2) = (k/2)^2 : 最小値
((x + k)/3)^3/x >= (k/2)^2
となります。ただし，等号は，x = k/2 のときです。
そこで，x = a > 0, k = b + c > 0 とおくと，
((a + b + c)/3)^3/a >= ((b + c)/2)^2
ただし，等号は，a = (b + c)/2 のときです。
ここで，右辺に問題１：の２項の場合の相加相乗平均を使うと，
((b + c)/2)^2 >= (√(bc))^2 = bc
ただし，等号は，b = c のときです。これより，
((a + b + c)/3)^3/a >= ((b + c)/2)^2 >= bc
((a + b + c)/3)^3 >= abc
a, b, c は，正の実数なので，
(a + b + c)/3 >= (abc)^(1/3)
になります。ただし，等号は，a = (b + c)/2 かつ b = c なので，a = b = c のときです。

問題３：
同様にやってみます。
f(x) = ((x + k)/4)^4/x, x > 0, k > 0
f'(x) = {4 * ((x + k)/4)^3 * 1/4 * x - ((x + k)/4)^4 * 1}/x^2
= ((x + k)/4)^3 * {x - (x + k)/4}/x^2
= ((x + k)/4)^3 * 1/4 * (3x - k)/x^2
x > 0, k > 0 においては，
0 < x < k/3 で，f'(x) < 0，f(x) は 単調減少
x = k/3 で，f'(x) = 0，f(x) は 極小かつ最小
k/3 < x で，f'(x) > 0，f(x) は 単調増加
なので，
f(x) >= f(k/3) = (k/3)^3 : 最小値
((x + k)/4)^4/x >= (k/3)^3
となります。ただし，等号は，x = k/3 のときです。
そこで，x = a > 0, k = b + c + d > 0 とおくと，
((a + b + c + d)/4)^4/a >= ((b + c + d)/3)^3
ただし，等号は，a = (b + c + d)/3 のときです。
ここで，右辺に問題２：の３項の場合の相加相乗平均を使うと，
((b + c + d)/3)^3 >= ((bcd)^(1/3))^3 = bcd
ただし，等号は，b = c = d のときです。これより，
((a + b + c + d)/4)^4/a >= ((b + c + d)/3)^3 >= bcd
((a + b + c + d)/4)^4 >= abcd
a, b, c, d は，正の実数なので，
(a + b + c + d)/4 >= (abcd)^(1/4)
になります。ただし，等号は，a = (b + c + d)/3 かつ b = c = d なので，a = b = c =d のときです。

問題４：
同様にやってみます。
f(x) = ((x + k)/n)^n/x, x > 0, k > 0
f'(x) = {n * ((x + k)/n)^(n-1) * 1/n * x - ((x + k)/n)^n * 1}/x^2
= ((x + k)/n)^(n-1) * {x - (x + k)/n}/x^2
= ((x + k)/n)^(n-1) * 1/n * ((n-1)x - k)/x^2
x > 0, k > 0 においては，
0 < x < k/(n-1) で，f'(x) < 0，f(x) は 単調減少
x = k/(n-1) で，f'(x) = 0，f(x) は 極小かつ最小
k/(n-1) < x で，f'(x) > 0，f(x) は 単調増加
なので，
f(x) >= f(k/(n-1)) = (k/(n-1))^(n-1) : 最小値
((x + k)/n)^n/x >= (k/(n-1))^(n-1) ... (A)
となります。ただし，等号は，x = k/(n-1) のときです。
これを使って n 項の場合の相加相乗平均を証明しますが，数学的帰納法を用います。
２項の場合は，問題１：より明らかです。
そこで，(n-1)項の場合
(a1 + a2 + a3 + ... + a_(n-1))/n >= (a1a2a3...a_(n-1))^(1/(n-1))
ただし，等号は，a1 = a2 = a3 = ... = a_(n-1) のとき
を仮定します。
さて，(A) で，x = a1 > 0, k = a2 + a3 + ... + an > 0 とおくと，
((a1 + a2 + a3 + ... + an)/n)^n/a1 >= ((a2 + a3 + ... + an)/(n-1))^(n-1)
ただし，等号は，a1 = (a2 + a3 + ...+ an)/(n-1) のときです。
ここで，右辺に仮定の(n-1)項の場合の相加相乗平均を使うと，
a1 -> a2, a2 -> a3, ..., a_(n-1) -> an
と置き換えて，
((a2 + a3 + ... + an)/(n-1))^(n-1) >= ((a2a3...an)^(1/(n-1)))^(n-1) = a2a3...an
ただし，等号は，a2 = a3 = ... = an のときです。これより，
((a1 + a2 + a3 + ... + an)/n)^n/a1 >= ((a2 + a3 + ... + an)/(n-1))^(n-1) >= a2a3...an
((a1 + a2 + a3 + ... + an)/n)^n >= a1a2a3...an
a1, a2, a3, ..., an は，正の実数なので，
(a1 + a2 + a3 + ... + an)/n >= (a1a2a3...an)^(1/n)
になります。ただし，等号は，
a1 = (a2 + a3 + ... + an)/(n-1) かつ a2 = a3 = ... = an なので，a1 = a2 = a3 = ... = an のときです。

(感想)
相加相乗平均の証明はいろいろ知られているように記憶していますが，これもうまい方法ですね。
勉強になりました。

NO2「kashiwagi」 7/15 07時51分受信 更新8/3

お世話になります。相加平均と相乗平均の大小証明にこんな方法があったのですね。 いやはや眉から鱗が落ちるとは正にこの様なことを云うのでしょうか・・・・。 もう??年も前のことになるのですが、高校1年の授業ではこの様な手法は・・・・、やはり 進化しているのでしょうか、それとも小職が知らなかっただけなのでしょうか。うーんー。 兎も角、久しぶりに新鮮な驚きに頭脳が喜んでおります。 申し訳ございませんが、一般解さえ証明されれば後は随意ですので、解答はかなり省略 し、問題4のみ証明致しました。

210回解答

題意より　　を微分すると、

　となり、で極値をとることが分かる。

ｋは正の定数、ｘ＞0であるので、これに注意して増減を確かめると、以下の様になる。

ｘ
		0
	↘		↗

因って、ｘ＝　で最小値をとることが分かる。

即ち、となる。この式を変形すると、

　となる。ここで、ｘ＝a1、＝a2＝a3＝・・・・・・＝an＞0と置くと、

　となる。これで問題4が証明された。

問題1〜3も全く同様な考え方で用意に証明される。

NO3「kasama」 7/31 13時52分受信 更新8/3

相加平均・相乗平均の関係はよく知られています。その証明方法もいろいろありそうですが、凸型関数の最小値に関連付けての証明は知りませんでした。添付ファイルの通り解答をまとめましたので転送します。

関数f(x)=

^n

を微分すると、

f(x)'=

となり、f(x)'=0⇒x0=

で、ただ１つの極値をとります。

f(x)'をさらに微分して、

f(x)''=

ですが、x=x₀とすると、

f(x0)''=

^n-4

>0

なので、f(x₀)は極小かつ最小で、そのときの値は、

f(x0)=

^n-1

です。よって、

^n

≧

^n-1

⇒

^n

≧

^n-1

x

…(1)

です。これを基にして、問題を考えます。

問題１　(1)式で、n=2、k=a、x=bとすると、

^2

≧

ab

⇒

≧

(ab)^1/2

…(2)

となります。

問題２　(1)式で、n=3、k=a+b、x=cとすると、

^3

≧

^2

c

ですが、(2)式を適用すると、

^3

≧

abc

⇒

≧

(abc)^1/3

…(3)

となります。

問題３　(1)式で、n=4、k=a+b+c、x=dとして、同様にすると、

^4

≧

^3

d

≧

abcd

⇒

≧

(abcd)^1/4

…(4)

となります。

問題４　数学的帰納法で証明します。n=m-1(mは自然数)のとき、以下の不等式が成り立つと仮定します。

^m-1

≧

a1a2a3…am-1

…(5)

(1)式で、n=m、k=a₁+a₂+a₃+…+a_m-1、x=a_mとすると、

^m

≧

^m-1

am

ですが、(5)式を適用すると、

^m

≧

a1a2a3…am

⇒

≧

(a1a2a3…am)^1/m

となり、n=mのときも成り立ちます。よって、すべてのnついて、

≧

(a1a2a3…an)^1/n

が成り立ちます。

NO4「三角定規」 8/02 12時04分受信 更新8/3

[問題210] 解答 <三角定規>

相加平均≧相乗平均　の証明法はいくつか知っていましたが，今回のものは初めて知りました。いろいろな方法があるものですね。感心しました。

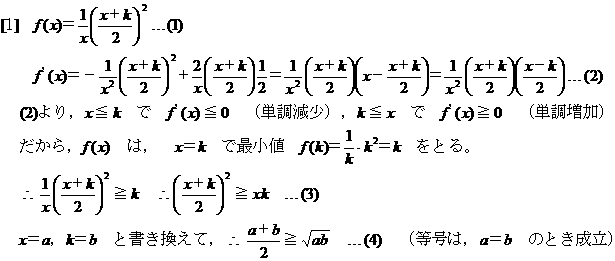
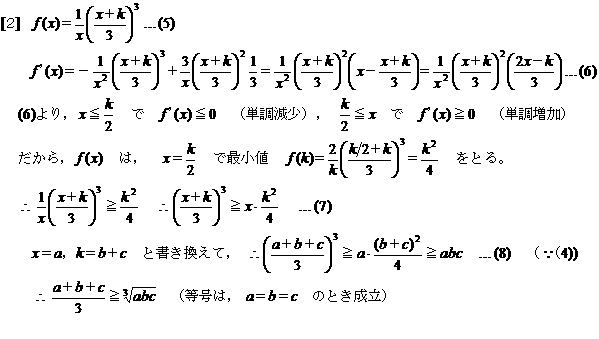
[４] 一般の場合も以上［１］〜［３］をもとにして帰納法で示すことができますが，添え字があまりに

　も煩雑になるので，以後省略します。すみません。