平成２１年１月１８日

[流れ星]

　　　　第２１８回数学的な応募問題解答

　　　　　　＜解答募集期間：12月28日〜1月18日

［バームクーヘン積分］

皆さん。バームクーヘン積分をご存知ですか。ある図形をｙ軸の周りに回転させてできる回転体の体積を求めるのに便利な公式です。ここで、今年の滋賀県立大学前期の問題を一部か改題して紹介します。

この問題を解くにあたって、バームクーヘン積分を参考にしても構いません。

NO1「uchinyan」 12/28 14時12分受信 更新1/18

＜コメント：今年一年，楽しく勉強させて頂き，ありがとうございました。
来年もよろしくお願い致します。＞

第２１８回数学的な応募問題
［バームクーヘン積分］

前回の第２１７回では，ヒントを見ずに解いたのですが，今回は見て解くことにします (^^;

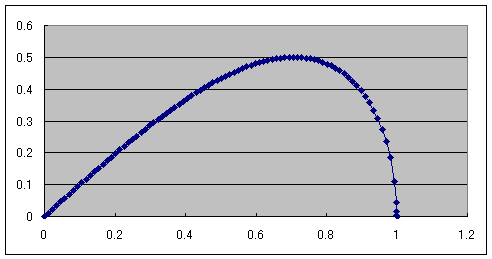
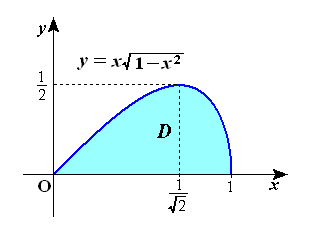
y = f(x) = x * sqrt(1 - x^2), 0 <= x <= 1
最初に，グラフの形状を調べておきます。
y' = f'(x) = sqrt(1 - x^2) + x * 1/2 * 1/sqrt(1 - x^2) * (-2x) = (1 - 2x^2)/sqrt(1 - x^2)
= - 2 * (x + sqrt(2)/2)(x - sqrt(2)/2)/sqrt(1 - x^2)
y'' = f''(x) = (- 4x * sqrt(1 - x^2) - (1 - 2x^2) * 1/2 * 1/sqrt(1 - x^2) * (-2x))/(1 - x^2)
= (- 4x + 4x^3 + x - 2x^3)/(sqrt(1 - x^2))^3
= 2x(x^2 - 3/2)/(sqrt(1 - x^2))^3
= 2x(x + sqrt(6)/2)(x -  sqrt(6)/2)/(sqrt(1 - x^2))^3
そこで，sqrt(6)/2 > 1 に注意すると，0 <= x <= 1 の範囲で，
x = 0　で　y = f(0) = 0
0 < x < sqrt(2)/2　で　単調増加　上に凸
x = sqrt(2)/2　で　極大値 = 最大値 = f(sqrt(2)/2) = 1/2
sqrt(2)/2 < x < 1　で　単調減少　上に凸
x = 1　で　y = f(1) = 0　接線の傾きは -∞
になります。
以上に注意して解きます。

(1)
S = ∫[x=0,1]ydx = ∫[x=0,1]{x * sqrt(1 - x^2)}dx
t = 1 - x^2 とおくと，dt/dx = - 2x，dx/dt = - 1/2x，t : 1 -> 0 なので，
= ∫[t=1,0]{x * sqrt(t) * (- 1/2x)}dt
= ∫[t=0,1]{1/2 * t^(1/2)}dt
= [1/3 * t^(3/2)][t=0,1]
= 1/3

(2)
x 軸回りの回転体の体積の公式より，
Vx = ∫[x=0,1]{πy^2}dx = π∫[x=0,1]{(x * sqrt(1 - x^2))^2}dx
= π∫[x=0,1]{x^2 * (1 - x^2)}dx
= π∫[x=0,1]{x^2 - x^4}dx
= π[x^3/3 - x^5/5][x=0,1]
= π(1/3 - 1/5)
= 2π/15

(3)
ヒントの「バームクーヘン積分」を使います。
Vy = ∫[x=0.1]{2πxf(x)}dx
= 2π∫[x=0,1]{x^2 * sqrt(1 - x^2)}dx
x = sinθ とおくと，dx/dθ = cosθ，θ : 0 -> π/2 なので，
= 2π∫[θ=0,π/2]{(sinθ)^2 * sqrt(1 - (sinθ)^2) * cosθ}dθ
= 2π∫[θ=0,π/2]{(sinθcosθ)^2}dθ
= 2π∫[θ=0,π/2]{(sin2θ)^2/4}dθ
= π/2 * ∫[θ=0,π/2]{(1 - cos4θ)/2}dθ
= π/4 * [θ - sin4θ/4][θ=0,π/2]
= π^2/8

(別解)
通常の y 軸回りの回転体の公式を使って検算しておきます。
y = x * sqrt(1 - x^2)
y^2 = x^2 * (1 - x^2) = x^2 - x^4
x^4 - x^2 + y^2 = 0
グラフより 0 <= y <= 1/2 なので，x^2 の二次方程式だと思うと，
x^2 = (1 - sqrt(1 - 4y^2))/2 or (1 + sqrt(1 - 4y^2))/2
と実数の範囲で書けます。
ここで，
x1^2 = (1 - sqrt(1 - 4y^2))/2　は，0 <= x <= sqrt(2)/2　に対応。
x2^2 = (1 + sqrt(1 - 4y^2))/2　は，sqrt(2)/2 <= x <= 1　に対応。
に注意します。すると，
Vy = ∫[y=0,1/2]{π(x2)^2}dy - ∫[y=0,1/2]{π(x1)^2}dy
= π∫[y=0,1/2]{(1 + sqrt(1 - 4y^2))/2 - (1 - sqrt(1 - 4y^2))/2}dy
= π∫[y=0,1/2]{sqrt(1 - 4y^2)}dy
y = sinθ/2 とおくと，dy/dθ = cosθ/2，θ : 0 -> π/2 なので，
= π∫[θ=0,π/2]{sqrt(1 - (sinθ)^2) * cosθ/2}dθ
= π/2 * ∫[θ=0,π/2]{(cosθ)^2}dθ
= π/2 * ∫[θ=0,π/2]{(1 + cos2θ)/2}dθ
= π/4 * [θ + sin2θ/2][θ=0,π/2]
= π^2/8
となり，確かに一致しています。

(考察)
ヒントで与えられているバームクーヘン積分のページの[2]は少しおかしいようです。
正しくは次のようになるのでは？

[2] 関数 y = f(x) が区間 [a,b] で単調性減少のとき
Vy = π * b^2 * c + ∫[y=c,d]{πx^2}dy - π * a^2 * d
= π * b^2 * c - π * a^2 * d + ∫[x=b,a]{π * x^2 * f'(x)}dx
= π * b^2 * c - π * a^2 * d + [π * x^2 * f(x)][x=b,a] - ∫[x=b,a]{2πxf(x)}dx
= π * b^2 * c - π * a^2 * d + (π * a^2 * d - π * b^2 * c) - ∫[x=b,a]{2πxf(x)}dx
= - ∫[x=b,a]{2πxf(x)}dx
= ∫[x=a,b]{2πxf(x)}dx

また，[3]が少し分かりずらいですが，要するに，単調性のある区間に分けて足し上げればよく，
結果は，全体の区間を [a,b] とすると，同じく，∫[x=a,b]{2πxf(x)}dx になる，
ということですね。

なお，バームクーヘン積分は，要するに，y = f(x) のとき，
y 軸から x だけ離れた幅が微小 dx の円環を考えると，その体積が 2πx * f(x) * dx なので，
それを x = a 〜 b で積分して ∫[x=a,b]{2πxf(x)}dx になる，
と，直感的に捉えた方が分かりやすいかもしれません。

(感想)
前回に続き，便利な公式ですね。高校生のときには知りませんでした。
今の高校生は，いろいろと便利なものがあっていいなぁ。
なお、いろいろと楽しく勉強させて頂いて，ありがとうございました。

NO2「新俳人澄朝」01/05 10時46分受信 更新1/18

＜コメント：明けましておめでとうございます。今年もよろしくお願いします。「バームクーヘン積分」の解答を送付します。楽しく取り組めました。＞

NO3「浜田明巳」　01/05 13時00分受信 更新1/18

<コメント：明けましておめでとうございます。今年もよろしくお願いします。＞

ｆ(ｘ)＝ｘ(１−ｘ^２)^１／２（０≦ｘ≦１）において，
(1) ０≦ｘ≦１から，ｆ(ｘ)＝０⇔ｘ＝０ or １
　またｆ(ｘ)≧０であるから，面積Ｓは，
　Ｓ＝∫_{（ｘ：０〜１）}ｘ(１−ｘ^２)^１／２ｄｘ
　　＝−１／２・∫_{（ｘ：０〜１）}(１−ｘ^２)^１／２(１−ｘ^２)'ｄｘ
　　＝−１／２・[２／３・(１−ｘ^２)^３／２]_{（ｘ：０〜１）}
　　＝−１／２・(−２／３)＝１／３………(答)
(2) (1)から，体積Ｖは，
　Ｖ＝π∫_{（ｘ：０〜１）}{ｘ(１−ｘ^２)^１／２}^２ｄｘ
　　＝π∫_{（ｘ：０〜１）}ｘ^２(１−ｘ^２)ｄｘ
　　＝π∫_{（ｘ：０〜１）}(ｘ^２−ｘ^４)ｄｘ
　　＝π[１／３・ｘ^３−１／５・ｘ^５]_{（ｘ：０〜１）}
　　＝π(１／３−１／５)＝２π／１５………(答)
(3) ｆ'(ｘ)＝(１−ｘ^２)^１／２＋ｘ・１／２・(−２ｘ)／(１−ｘ^２)^１／２
　　　　　 ＝{(１−ｘ^２)−ｘ^２)}／(１−ｘ^２)^１／２
　　　　　 ＝(１−２ｘ^２)／(１−ｘ^２)^１／２
　０≦ｘ≦１から，０＜ｘ＜１／√２で，ｆ'(ｘ)＞０，１／√２＜ｘ＜１で，ｆ'(ｘ)＜０
　故にｆ(ｘ)は，ｘ＝１／√２で極大かつ最大となり，最大値は，ｆ(１／√２)＝１／２
　ｆ(ｘ)のグラフの１／√２≦ｘ≦１の部分をｙ軸で回転したときの体積Ｖ_１は，
　Ｖ_１＝π∫_{（ｙ：０〜１／２）}ｘ^２ｄｙ
　　 ＝π∫_{（ｘ：１〜１／√２）}ｘ^２・(１−２ｘ^２)／(１−ｘ^２)^１／２ｄｘ
　ｘ＝cosθ（０≦θ≦π／２）とすると，
　Ｖ_１＝π∫_{（θ：０〜π／４）}cos^２θ・(１−２cos^２θ)／sinθ・(−sinθ)ｄθ
　　 ＝π∫_{（θ：０〜π／４）}(１＋cos２θ)／２・cos２θｄθ
　　 ＝π／２・∫_{（θ：０〜π／４）}(cos２θ＋cos^２２θ)ｄθ
　　 ＝π／２・∫_{（θ：０〜π／４）}{cos２θ＋(１＋cos４θ)／２}ｄθ
　　 ＝π／４・∫_{（θ：０〜π／４）}(１＋２cos２θ＋cos４θ)ｄθ
　　 ＝π／４・[θ＋sin２θ＋１／４・sin４θ]∫_{（θ：０〜π／４）}
　　 ＝π／４・(π／４＋１)
　ｆ(ｘ)のグラフの０≦ｘ≦１／√２の部分をｙ軸で回転したときの体積Ｖ_２は，同様に，
　Ｖ_２＝π∫_{（ｙ：０〜１／２）}ｘ^２ｄｙ
　　 ＝π∫_{（ｘ：０〜１／√２）}ｘ^２・(１−２ｘ^２)／(１−ｘ^２)^１／２ｄｘ
　　 ＝π∫_{（θ：π／２〜π／４）}cos^２θ・(１−２cos^２θ)／sinθ・(−sinθ)ｄθ
　　 ＝−π／４∫_{（θ：π／４〜π／２）}(１＋２cos２θ＋cos４θ)ｄθ
　　 ＝−π／４・[θ＋sin２θ＋１／４・sin４θ]_{（θ：π／４〜π／２）}
　　 ＝−π／４・(π／４−１)
　故に求める体積Ｖは，
　Ｖ＝Ｖ_１−Ｖ_２
　　＝π／４・(π／４＋１)＋π／４・(π／４−１)
　　＝π^２／８………(答)
（別解）バームクーヘン積分の公式より，体積Ｖは，
　Ｖ＝２π∫_{（ｘ：０〜１）}ｘ・ｘ(１−ｘ^２)^１／２ｄｘ
　　＝２π∫_{（ｘ：０〜１）}ｘ^２(１−ｘ^２)^１／２ｄｘ
　ｘ＝sinθ（０≦θ≦π／２）とすると，
　Ｖ＝２π∫_{（θ：０〜π／２）}sin^２cosθ・cosθｄθ
　　＝π／２・∫_{（θ：０〜π／２）}sin^２２θｄθ
　　＝π／４・∫_{（θ：０〜π／２）}(１−cos４θ)ｄθ
　　＝π／４・[θ−１／４・sin４θ]_{（θ：０〜π／２）}
　　＝π^２／８

NO4「kashiwagi」 01/06 19時58分受信 更新1/18

＜コメント：あけましておめでとうございます。本年も宜しくお願い申し上げます。

今回の問題は昔良くやった積分演習を思い出しながら解いていきまし た。見た目よりは素直な問題でした。 ＞

218回解答

　　より　　よって　で極値をとる。その値前後の正負を調べ、極大値であることが分かる。これより種々の値を代入してグラフを描くと、以下の様になる。

ｘ₁

ｘ₂

　以上の準備に基づき（1）〜（3）を解くと、

（1）　

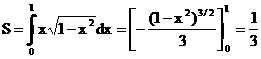
（2）　

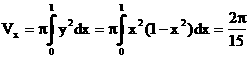
（3）上図に示したようにｘをとれば、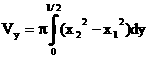であるから、

　より　となる。これより

正にこれがｘ₁とｘ₂であるから、上記積分式に代入すると、

　　

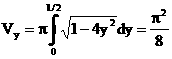
これは　の円の半周面積　π/8を考えれば容易に分かる。

NO5「三角定規」 01/17 10時37分受信 更新1/18

● 第218回 解答 <三角定規>

[問題１]　グラフとx軸で囲まれた部分D の面積 S

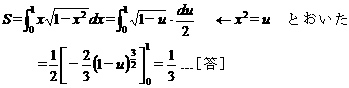
[問題２]　D をx軸の回りに回転した立体の体積 V1

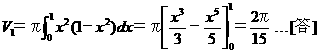
[問題３]　 D をy軸の回りに回転した立体の体積 V2 … バームクーヘン積分の公式より

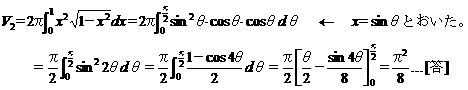
＜コメント：バームクーヘン積分の公式，前回の斜回転体の体積公式とともにすごい公式ですね。また，どなたが命名したのでしょうか，この名前も本質を言い当てていて感心します。

この公式を知るのも私は今回初めてなのですが，　数学屋さんの間ではポピュラーなものなのでしょうか？＞

＜水の流れ：私は平成の初めごろに県の研究会で発表された方から知りえました。

最初はうまい方法があることに驚きをもっていましたが、

　その先生はアメリカに留学し、帰国した生徒が待ちかえったテキストを見たことから、

発表されたようです。ネイミングがその本にあったようです。

最近、高校の範囲外ではありますが、理解されている先生は多いようです。＞

皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、
メールで送ってください。待っています。