�����Q�P�N�T���Q�S��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��Q�Q�S�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF�T���R���`�T���Q�S��
�m�K�i�̏��~���n
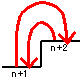
���}�̂悤�Ȃ��i�̊K�i������B���������ɂ��A�~���ɂ��A1�i���ł��A2�i���ł��悢���A�܂�1�i��2�i�Ƃ������Ă��悢�Ƃ���A�����č~���d���͉��ʂ肠�邩�B
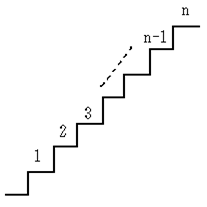 �������A1���~�̊Ԃɂ͊e�i�����Ȃ��Ƃ�1��͕K�����ނ��̂Ƃ���B
�������A1���~�̊Ԃɂ͊e�i�����Ȃ��Ƃ�1��͕K�����ނ��̂Ƃ���B
���̂Ƃ������č~���d���������i����2�ȏ�̎��R���j�Ƃ��āA���̏����œ�����B
��P�F�����Q�C�R�C�S�A�T�̂Ƃ��A���Q�@�C���R�@�@�C���S�@�C���T�̒l��
���ꂼ�ꋁ�߂�B
��Q�@�����{�Q�������{�P�������ŕ\���Q���������߂�B
��R�@���������ŕ\���B
NO1�uuchinyan�v 5/03 15��57����M
�X�V5/24
��Q�Q�S�w�I�ȉ�����
�m�K�i�̏��~���n
���� 0 �i�ڂƂ��Ca �i�ڂ��� b �i�ڂɈړ�����̂� a -> b �Ə������Ƃɂ��܂��B
��1�F
(1) n = 1
01 : 0 -> 1 -> 0
�Ȃ̂ŁC
a(1) = 1
(2) n = 2
01 : 0 -> 1 -> 2 -> 1 -> 0
02 : 0 -> 1 -> 2 -> 0
03 : 0 -> 2 -> 1 -> 0
0 -> 2 -> 0 �́C1 �i�ڂ�ł��Ȃ��̂ŕs��
�Ȃ̂ŁC
a(2) = 3
(3) n = 3
01 : 0 -> 1 -> 2 -> 3 -> 2 -> 1 -> 0
02 : 0 -> 1 -> 2 -> 3 -> 2 -> 0
03 : 0 -> 1 -> 2 -> 3 -> 1 -> 0
04 : 0 -> 1 -> 3 -> 2 -> 1 -> 0
05 : 0 -> 1 -> 3 -> 2 -> 0
06 : 0 -> 2 -> 3 -> 2 -> 1 -> 0
07 : 0 -> 2 -> 3 -> 1 -> 0
�Ȃ̂ŁC
a(3) = 7
(4) n = 4
01 : 0 -> 1 -> 2 -> 3 -> 4 -> 3 -> 2 -> 1 -> 0
02 : 0 -> 1 -> 2 -> 3 -> 4 -> 3 -> 2 -> 0
03 : 0 -> 1 -> 2 -> 3 -> 4 -> 3 -> 1 -> 0
04 : 0 -> 1 -> 2 -> 3 -> 4 -> 2 -> 1 -> 0
05 : 0 -> 1 -> 2 -> 3 -> 4 -> 2 -> 0
06 : 0 -> 1 -> 2 -> 4 -> 3 -> 2 -> 1 -> 0
07 : 0 -> 1 -> 2 -> 4 -> 3 -> 2 -> 0
08 : 0 -> 1 -> 2 -> 4 -> 3 -> 1 -> 0
09 : 0 -> 1 -> 3 -> 4 -> 3 -> 2 -> 1 -> 0
10 : 0 -> 1 -> 3 -> 4 -> 3 -> 2 -> 0
11 : 0 -> 1 -> 3 -> 4 -> 2 -> 1 -> 0
12 : 0 -> 1 -> 3 -> 4 -> 2 -> 0
13 : 0 -> 2 -> 3 -> 4 -> 3 -> 2 -> 1 -> 0
14 : 0 -> 2 -> 3 -> 4 -> 3 -> 1 -> 0
15 : 0 -> 2 -> 3 -> 4 -> 2 -> 1 -> 0
16 : 0 -> 2 -> 4 -> 3 -> 2 -> 1 -> 0
17 : 0 -> 2 -> 4 -> 3 -> 1 -> 0
�Ȃ̂ŁC
a(4) = 17
(5) n = 5
01 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 4 -> 3 -> 2 -> 1
-> 0
02 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 4 -> 3 -> 2 -> 0
03 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 4 -> 3 -> 1 -> 0
04 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 4 -> 2 -> 1 -> 0
05 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 3 -> 2 -> 1 -> 0
06 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 4 -> 2 -> 0
07 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 3 -> 2 -> 0
08 : 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 3 -> 1 -> 0
09 : 0 -> 1 -> 2 -> 3 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
10 : 0 -> 1 -> 2 -> 3 -> 5 -> 4 -> 3 -> 2 -> 0
11 : 0 -> 1 -> 2 -> 3 -> 5 -> 4 -> 3 -> 1 -> 0
12 : 0 -> 1 -> 2 -> 3 -> 5 -> 4 -> 2 -> 1 -> 0
13 : 0 -> 1 -> 2 -> 3 -> 5 -> 4 -> 2 -> 0
14 : 0 -> 1 -> 2 -> 4 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
15 : 0 -> 1 -> 2 -> 4 -> 5 -> 4 -> 3 -> 2 -> 0
16 : 0 -> 1 -> 2 -> 4 -> 5 -> 4 -> 3 -> 1 -> 0
17 : 0 -> 1 -> 2 -> 4 -> 5 -> 3 -> 2 -> 1 -> 0
18 : 0 -> 1 -> 2 -> 4 -> 5 -> 3 -> 2 -> 0
19 : 0 -> 1 -> 2 -> 4 -> 5 -> 3 -> 1 -> 0
20 : 0 -> 1 -> 3 -> 4 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
21 : 0 -> 1 -> 3 -> 4 -> 5 -> 4 -> 3 -> 2 -> 0
22 : 0 -> 1 -> 3 -> 4 -> 5 -> 4 -> 2 -> 1 -> 0
23 : 0 -> 1 -> 3 -> 4 -> 5 -> 3 -> 2 -> 1 -> 0
24 : 0 -> 1 -> 3 -> 4 -> 5 -> 4 -> 2 -> 0
25 : 0 -> 1 -> 3 -> 4 -> 5 -> 3 -> 2 -> 0
26 : 0 -> 2 -> 3 -> 4 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
27 : 0 -> 2 -> 3 -> 4 -> 5 -> 4 -> 3 -> 1 -> 0
28 : 0 -> 2 -> 3 -> 4 -> 5 -> 4 -> 2 -> 1 -> 0
29 : 0 -> 2 -> 3 -> 4 -> 5 -> 3 -> 2 -> 1 -> 0
30 : 0 -> 2 -> 3 -> 4 -> 5 -> 3 -> 1 -> 0
31 : 0 -> 1 -> 3 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
32 : 0 -> 1 -> 3 -> 5 -> 4 -> 3 -> 2 -> 0
33 : 0 -> 1 -> 3 -> 5 -> 4 -> 2 -> 1 -> 0
34 : 0 -> 1 -> 3 -> 5 -> 4 -> 2 -> 0
35 : 0 -> 2 -> 3 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
36 : 0 -> 2 -> 3 -> 5 -> 4 -> 3 -> 1 -> 0
37 : 0 -> 2 -> 3 -> 5 -> 4 -> 2 -> 1 -> 0
38 : 0 -> 2 -> 4 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
39 : 0 -> 2 -> 4 -> 5 -> 4 -> 3 -> 1 -> 0
40 : 0 -> 2 -> 4 -> 5 -> 3 -> 2 -> 1 -> 0
41 : 0 -> 2 -> 4 -> 5 -> 3 -> 1 -> 0
�Ȃ̂ŁC
a(6) = 41
������C��2�F���ӎ����āC�Q�������ۂ��l���Ă݂܂��B
5 �i�ڂ܂ŏ����č~���̂́C
1) �r�� 4 �i�ڂ܂ŏ����č~���ꍇ�́C���̌�C
4 -> 5 -> 4
�Ȃ̂ŁCa(4) * 1 = a(4) �ʂ�B
2) �r�� 3 �i�ڂ܂ŏ����č~���ꍇ�́C���̌�C
����~��Ƃ� 4 �i�ڂ��o�R����̂� 1) �Ɋ܂܂��̂ŁC����������āC
3 -> 4 -> 5 -> 3
3 -> 5 -> 4 -> 3
3 -> 5 -> 3 �� 4 �i�ڂ܂Ȃ��̂ŕs��
�Ȃ̂ŁCa(3) * 2 = 2 * a(3) �ʂ�B
3) �r�� 2 �i�ڂ܂ŏ����č~���ꍇ�́C���̌�C
����~��Ƃ� 4, 3 �i�ڂ��o�R����̂� 1), 2) �Ɋ܂܂��̂ŁC����������āC
2 -> 3 -> 5 -> 4 -> 2
2 -> 4 -> 5 -> 3 -> 2
�����Ȃ��̂ŁCa(2) * 2 = 2 * a(2) �ʂ�B
4) �r�� 1 �i�ڂ܂ŏ����č~���ꍇ�́C���̌�C
����~��Ƃ� 4, 3, 2 �i�ڂ��o�R����̂� 1),
2), 3) �Ɋ܂܂��̂ŁC����������āC
1 -> 2 -> 4 -> 5 -> 3 -> 1
1 -> 3 -> 5 -> 4 -> 2 -> 1
�����Ȃ��̂ŁCa(1) * 2 = 2 * a(1) �ʂ�B
�ȏ�ł��ׂĂȂ̂ŁC
a(5) = a(4) + 2 * a(3) + 2 * a(2) + 2 * a(1)
�ɂȂ�܂��B
a(4) �ɂ��Ă����l�̂��Ƃ��l����ƁC
a(3) �o�R�F3 -> 4 -> 3
a(2) �o�R�F2 -> 3 -> 4 -> 2, 2 -> 4 -> 3
-> 2
a(1) �o�R�F1 -> 2 -> 4 -> 3 -> 1, 1 -> 3
-> 4 -> 2 -> 1
�Ȃ̂ŁC
a(4) = a(3) + 2 * a(2) + 2 * a(1)
�ł��B�����ŁC
a(5) - a(4) = a(4) + a(3)
a(5) = 2 * a(4) + a(3) = 2 * 17 + 7 = 34 + 7 = 41
�ɂȂ�܂��B�m���ɁC�n���ɐ��������̂ƈ�v���Ă��܂��B
��2�F
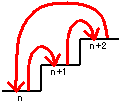
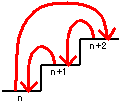
��1�G��(5)�̌㔼�ōl�������@����ʉ����܂��Bn = 1, 2, 3,... �Ƃ��܂��B
n+2 �i�ڂ܂ŏ����č~���̂́C
1) �r�� n+1 �i�ڂ܂ŏ����č~���ꍇ�́C���̌�C
n+1 -> n+2 -> n+1
�Ȃ̂ŁCa(n+1) * 1 = a(n+1) �ʂ�B
2) �r�� n �i�ڂ܂ŏ����č~���ꍇ�́C���̌�C
����~��Ƃ� n+1 �i�ڂ��o�R����̂� 1) �Ɋ܂܂��̂ŁC����������āC
n -> n+1 -> n+2 -> n
n -> n+2 -> n+1 -> n
n -> n+2 -> n �� n+1 �i�ڂ܂Ȃ��̂ŕs��
�Ȃ̂ŁCa(n) * 2 = 2 * a(n) �ʂ�B
3) �r�� k �i�ځC1 <= k <= n-1�C�܂ŏ����č~���ꍇ�́C���̌�C
����~��Ƃ� n+1, n, ..., k+1 �i�ڂ̂��������i���o�R����̂́C���̏ꍇ�Ɋ܂܂��̂ŁC����������܂��B
����ƁC�~��閔�͏���̂� 1 �i���� 2 �i�Ȃ̂ŁCk �` n+2 �̊ԂŁC
�E1 �i�������ď�������~�肽�肪�N����ꍇ
�E1 �i + 2 �i ���� 2 �i + 1 �i ���N����ꍇ
�́C����~��̉����ŁC�K���C���Ȃ��Ƃ�������i���o�R���邱�Ƃ�������̂ŁC
���ꂪ k �i�ږ��� n+2 �i�ڂŋN����ꍇ�ȊO�������܂��B
�����ʼn\�Ȃ̂́C1 �i + 2 �i�C2 �i + 1 �i �����[�ŋN���邩�C2
�i�������ŏ���ꍇ�����ł��B
�������C�i��K�����܂Ȃ��Ƃ����Ȃ��̂ŁC���ǁC
�En+2-k �������̏ꍇ
k -> k+1 -> k+3 -> ...(2 �i����)... -> n-1
-> n+1 -> n+2 -> n -> ...(2 �i����)... ->
k+2 -> k
k -> k+2 -> ...(2 �i����)... -> n -> n+2 ->
n+1 -> n-1 -> ...(2 �i����)... -> k+3 -> k+1
-> k
�En+2-k ����̏ꍇ
k -> k+1 -> k+3 -> ...(2 �i����)... -> n ->
n+2 -> n+1 -> n-1 -> ...(2 �i����)... -> k+2
-> k
k -> k+2 -> ...(2 �i����)... -> n-1 -> n+1
-> n+2 -> n -> ...(2 �i����)... -> k+3 ->
k+1 -> k
�����ł��B�����ŁCa(k) * 2 = 2 * a(k) �ʂ�B
�ȏ�ł��ׂĂȂ̂ŁC
a(n+2) = a(n+1) + 2 * a(n) + 2 * a(n-1) + ... + 2 * a(2) + 2 * a(1)
�ɂȂ�܂��B���l�ɂ��āC
a(n+1) = a(n) + 2 * a(n-1) + 2 * a(n-2) + ... + 2 * a(2) + 2 * a(1)
�Ȃ̂ŁC
a(n+2) - a(n+1) = a(n+1) + a(n)
a(n+2) = 2 * a(n+1) + a(n)
�ɂȂ�܂��B�������Cn = 1, 2, 3, ... �ŁCa(1)
= 1, a(2) = 3 �ł��B
��3�F
a(n+2) = 2 * a(n+1) + a(n), n = 1, 2, 3, ...
a(1) = 1, a(2) = 3
�����������ł��B�������J�ɂ���Ă݂܂��傤�B
�悭���悤�ɁC
a(n+2) - p * a(n+1) = q * (a(n+1) - p * a(n))
�Ƃ����`�ɕό`���邱�Ƃ��l���܂��B����́C
a(n+2) - (p + q) * a(n+1) + pq * a(n) = 0
�Ə����܂��B���̑Q�����́C
a(n+2) = 2 * a(n+1) + a(n)
a(n+2) - 2 * a(n+1) - a(n) = 0
��r����ƁC
p + q = 2
pq = -1
�ƂȂ�悤�ɁCp, q �����߂�����ł��B
���� p, q �́C���� t �ɂ��Ă̓������̉��ɂȂ�܂��B
t^2 - 2t - 1 = 0
t = 1 - sqrt(2), 1 + sqrt(2)
�����ŁC
p = 1 - sqrt(2), q = 1 + sqrt(2)
�Ƃ��܂��B���� p, q �ɑ��āC
a(n+2) - p * a(n+1) = q * (a(n+1) - p * a(n))
a(n+2) - p * a(n+1) = q^n * (a(2) - p * a(1))
a(n+1) - p * a(n) = q^(n-1) * (a(2) - p * a(1))�@... (A)
�܂��C
a(n+2) - (p + q) * a(n+1) + pq * a(n) = 0
�́C
a(n+2) - q * a(n+1) = p * (a(n+1) - q * a(n))
�Ƃ��ό`�ł���̂ŁC
a(n+2) - q * a(n+1) = p^n * (a(2) - q * a(1))
a(n+1) - q * a(n) = p^(n-1) * (a(2) - q * a(1))�@... (B)
�����ŁC(A) - (B) ���C
(q - p) * a(n) = (a(2) - p * a(1)) * q^(n-1) - (a(2) - q * a(1)) * p^(n-1)
q - p = 2 * sqrt(2) not= 0 �Ȃ̂ŁC
a(n) = {(a(2) - p * a(1)) * q^(n-1) - (a(2) - q * a(1)) * p^(n-1)}/(q - p)
p = 1 - sqrt(2), q = 1 + sqt(2), a(1) = 1, a(2) = 3 �������āC
a(n) = {(3 - (1 - sqrt(2)) * 1) * (1 + sqrt(2))^(n-1) - (3 - (1 + sqrt(2)) * 1)
* (1 - sqrt(2))^(n-1)}/((1 + sqrt(2)) - (1 - sqrt(2)))
a(n) = {(2 + sqrt(2)) * (1 + sqrt(2))^(n-1) - (2 - sqrt(2)) * (1 -
sqrt(2))^(n-1)}/(2 * sqrt(2))
a(n) = ((1 + sqrt(2))^(n-1) - (1 - sqrt(2))^(n-1))/sqrt(2) + ((1 +
(sqrt(2))^(n-1) + (1 - sqrt(2))^(n-1))/2
�Ō�̎��͌v�Z���y�ɂȂ�悤�ɂ��܂����B�����āC�m���ɁC
a(1) = ((1 + sqrt(2))^0 - (1 - sqrt(2))^0)/sqrt(2) + ((1 + (sqrt(2))^0 + (1 -
sqrt(2))^0)/2
= 0 + 2/2
= 1
a(2) = ((1 + sqrt(2))^1 - (1 - sqrt(2))^1)/sqrt(2) + ((1 + (sqrt(2))^1 + (1 -
sqrt(2))^1)/2
= 2 + 1
= 3
a(3) = ((1 + sqrt(2))^2 - (1 - sqrt(2))^2)/sqrt(2) + ((1 + (sqrt(2))^2 + (1 -
sqrt(2))^2)/2
= 4 + 3
= 7
a(4) = ((1 + sqrt(2))^3 - (1 - sqrt(2))^3)/sqrt(2) + ((1 + (sqrt(2))^3 + (1 -
sqrt(2))^3)/2
= 10 + 7
= 17
a(5) = ((1 + sqrt(2))^4 - (1 - sqrt(2))^4)/sqrt(2) + ((1 + (sqrt(2))^4 + (1 -
sqrt(2))^4)/2
= 24 + 17
= 41
�ƂȂ��āC��1�F�̌��ʂƈ�v���܂��B
(���z)
���邾���C�~�邾���Ȃ�C�t�B�{�i�b�`����ɂȂ邱�Ƃ͂悭�m���Ă��܂����C
����~��͏��߂Č��܂����B�����悤�ȑQ�����ɂȂ�̂ł��ˁB
NO2�uBossF�v 5/08 5��33����M �X�V5/24
N�i�̊K�i�̏�����i���~����j�������Ƃ���Ƃ���������^2
����N�i�ɏ��邽�߂ɂ́AN�|1�i�ڂ���1�i���邩�AN-2�i�ڂ���2�i���邩�̂����ꂩ������
����������-1+����-2
�ȏ���ȉ���
��P�@���Q��4�@���R��9�@���S��25�@���T��64
��Q�@�����{�Q��{sqrt (�����{�P) +sqrt (����)}^2
��R �osqrt (����) }�@��fibonacci�ł��邩��A������(1/5)[ {(1+��5)/2}^n-{(1-��5)/2}^n]^2
�����̗���R�����g�F���肩�܂��͍~��̂Ƃ��K����x�K�i��ł����܂�����A�t�B�{�i�b�`����̕����ɂ͂Ȃ�܂���B��
NO3�ukashiwagi�v
5/11 12��22����M
�ukashiwagi�v 5/22 22��16����M �X�V5/24
224���
��1.
���A��i�����1�A2�i�����2�ƕ\����
�@
����2�̂Ƃ��́A�����1-2��2��2��ށB�����č~���������2��ށB
�A���A������~���2�A2�Ƃ����1�͓��܂Ȃ����ɂȂ�̂�a2
= 2�~2-1��3�A
�A
����3�̂Ƃ��́A�����1-2-3�A2-3�����1-3��3��ށB�����č~���������3��ށB
�A���A������~���2-3�����1-3�̏ꍇ��1��2�܂Ȃ��̂�a3= 3�~3-2��7
�ȏ�̍l�����P���A���̌��𑝂₵�čl����ƈȉ��̗l�ɂȂ�B
a2 = 2�~2-1��3
a3= 3�~3-2��7
a4 = 5�~5-8��17
a5=8�~8-23��41
a6=13�~13-70��99
��2.
�@��1�̌��ʂ�ǂ�����ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �@�@�ƂȂ��Ă��邱�Ƃ�������B
�@�@�ƂȂ��Ă��邱�Ƃ�������B
��3.
���A������![]() ��2�������A���i�������j�Ƃ����
��2�������A���i�������j�Ƃ����
��+����2�A������-1�ł��邩���2�̌��ʂ��g��
![]() �@�E�E�E�E�E�E�E�E�E�E�@�@�ƂȂ�B������ό`����
�@�E�E�E�E�E�E�E�E�E�E�@�@�ƂȂ�B������ό`����
�@![]()
�����A����![]() �͌�����̓��䐔��ł��邩��
�͌�����̓��䐔��ł��邩��
![]() �@�E�E�E�E�E�E�A�@�ƂȂ�B
�@�E�E�E�E�E�E�A�@�ƂȂ�B
![]() �@�@�E�E�E�E�E�E�B�@�ƂȂ�B
�@�@�E�E�E�E�E�E�B�@�ƂȂ�B
�����ŇA����чB��a2 ��3�Aa3�@��7�������A������i�����A
![]() �@�E�E�E�E�E�E�C�@��B
�@�E�E�E�E�E�E�C�@��B
�����ŁA���ƃ��̒l�����߂�ƁA![]() �@�A
�@�A![]() �ł��邩��A�������
�ł��邩��A�������![]() �@�ƂȂ�B
�@�ƂȂ�B
�ȁ@�@�@��D�@
NO4�ukasama�v 5/21 15��15����M �X�V5/24
|
��1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��3 |
|
���R�����g�F����̓t�B�{�i�b�`����Ɏ����K�i�̏���~��̖��ł��ˁB
�����ȃA�v���[�`������Ǝv���܂����A�K�i�̏���~����R��ނɃp�^�[���������čl���܂����B
����قǍ��x�Ȑ��w�̒m�����Ȃ��Ƃ����g�߂��y���������Ǝv���܂��B��
�F����A�������킩������A�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA
���[���ő����Ă��������B�҂��Ă��܂��B
![]()