暯惉俀侾擭侾侾寧俀俀擔
 [棳傟惎]
[棳傟惎]
丂丂丂丂丂戞俀俁俁夞悢妛揑側墳曞栤戣
丂丂丂丂丂丂亙夝摎曞廤婜娫丗11寧22擔乣12寧13擔
乵俇値乕侾偺慺悢乶
奆偝傫丄崱擭偺愮梩戝妛擖帋栤戣偺拞偱丄慺悢偺娭偡傞栤戣偑偁傝傑偟偨丅
乮侾乯俆埲忋偺慺悢偼丄偁傞帺慠悢値傪傕梡偄偰俇値亄侾傑偨偼俇値亅侾偺宍偵昞偝傟傞偙偲傪帵偣丅
乮俀乯俶傪帺慠悢偲偡傞丅俇俶亅侾偼丄俇値乗侾乮値偼帺慠悢乯偺宍偱昞偝傟傞慺悢傪栺悢偵傕偮偙偲傪帵偣丅
乮俁乯俇値乗侾乮値偼帺慠悢乯偺宍偱昞偝傟傞慺悢偼柍尷偵懡偔懚嵼偡傞偙偲傪帵偣丅
NO1乽uchinyan乿 11/22 16帪15暘庴怣 峏怴12/13
戞俀俁俁夞悢妛揑側墳曞栤戣
乵俇値乕侾偺慺悢乶
(1)
4 埲忋偺惍悢偼丆昁偢丆n 傪帺慠悢偲偟偰丆6n-2丆6n-1丆6n丆6n+1丆6n+2丆6n+3 偲昞偣傑偡偑丆
5 埲忋偺慺悢偼丆2 偺攞悢偱傕丆3 偺攞悢偱傕側偄偺偱丆昁偢丆6n-1 枖偼 6n+1 偺宍偵側傝傑偡丅
(2)
6N-1 偑 6n-1 宆偺慺悢傪栺悢傕偨側偄偲偟傑偡丅
偡傞偲丆(1)傛傝丆6n+1 宆偺慺悢偩偗傪栺悢丆慺場悢丆偵傕偮偙偲偵側傝傑偡偑丆堦斒偵丆
(6k+1)(6m+1) = 6(6km+k+m)) + 1
偲側傝丆 6n+1 宆偺慺悢傪偄偔傜妡偗偰傕 6 偱妱偭偰 +1 梋傞悢偟偐偱偒偢丆6N-1 宆偺惍悢偵側傝傑偣傫丅
偦偙偱丆彮側偔偲傕 1 屄丆堦斒偵偼婏悢屄丆偺 6n-1 宆偺慺場悢丆偮傑傝偼栺悢丆傪昁偢傕偮偙偲偵側傝傑偡丅
(3)
6n-1 宆偺慺悢偑桳尷屄偟偐側偄偲偟傑偡丅偦偟偰丆偦傟傜偺愊傪 N 偲偟傑偡丅N 偼傕偪傠傫帺慠悢偱偡丅
偙偙偱丆6N-1 偲偄偆惍悢傪嶌傞偲丆桳尷屄偺偳偺 6n-1 宆偺慺悢偱妱偭偰傕丆N 傪妱傝愗偭偰偟傑偄丆
6N-1 帺懱傪妱傝愗傞偙偲偼偁傝傑偣傫丅
偲偙傠偑丆(2)傛傝丆6N-1 偼 6n-1 宆偺慺悢傪昁偢栺悢偵傕偪傑偡丅
偙傟偼柕弬偱偡丅
偟偨偑偭偰丆6n-1 宆偺慺悢偼柍尷屄偁傞偙偲偵側傝傑偡丅
(峫嶡)
6n+1 宆偺慺悢偵娭偟偰偼丆彮側偔偲傕丆忋婰偺曽朄偱偼桳尷屄偐柍尷屄偐暘偐傜側偄傛偆偱偡丅
6n-1 宆偺慺悢傪嬼悢屄妡偗傞偲 6n+1 宆偺惍悢偵側偭偰偟傑偆偺偱丅
彮偟峫偊偰傒偨偺偱偡偑丆偙傫側姶偠偱偳偆偱偟傚偆偐丅
6n+1 宆偺慺悢偑桳尷屄偟偐側偄偲偟傑偡丅偦偟偰丆偦傟傜偺愊傪 N 偲偟傑偡丅N 偼傕偪傠傫帺慠悢偱偡丅
偙偙偱丆(6N)^3 + 1 偲偄偆惍悢傪嶌傞偲丆桳尷屄偺偳偺
6n+1 宆偺慺悢偱妱偭偰傕丆N 傪妱傝愗偭偰偟傑偄丆
(6N)^3 + 1 帺懱傪妱傝愗傞偙偲偼偁傝傑偣傫丅
偙偙偱丆傕偟丆(6N)^3 + 1 帺懱偑慺悢側傜偽丆
(6N)^3 + 1 = 6 * (6^2 * N^3) + 1 > N > 婛懚偺 6n+1 宆偺慺悢
偱丆怴偨側 6n+1 宆偺慺悢偵側傝丆6n+1 宆偺慺悢偑桳尷屄偱偁偭偨偙偲偵柕弬偟傑偡丅
(6N)^3 + 1 帺懱偑慺悢偱側偄応崌偼丆(6N)^3 + 1 偑 p 偲偄偆慺場悢傪傕偮偲偟傑偡丅柧傜偐偵 p 偼 5 埲忋偱偡丅
偡傞偲丆mod p 偱峫偊偰丆
(6N)^3 + 1 佭 0
(6N)^3 佭 -1
(6N)^6 佭 +1
偙偙偱丆p 偑 6N 傪妱傝愗傞偙偲偼側偄偺偱丆p 偑慺悢偱偁傞偙偲偐傜丆p 偲 6N 偼屳偄偵慺偲側傝丆
僼僃儖儅乕偺彫掕棟偐傜丆
(6N)^(p-1) 佭 +1
偙偺偙偲偲愭傎偳偺幃偐傜丆q 傪 0 埲忋偺惍悢丆r 傪 0 <= r <= 5 偺惍悢丆偲偟偰丆
p-1 = 6q + r
(6N)^(p-1) 佭 +1
(6N)^(6q + r) 佭 +1
((6N)^6)^q * (6N)^r 佭 +1
1 * (6N)^r 佭 +1
(6N)^r 佭 +1
丒r = 0 偺応崌
(6N)^0 佭 +1
p-1 = 6q丆p = 6q + 1
偙傟偼丆OK丅
丒r = 1 偺応崌
(6N)^1 佭 +1
(6N)^3 佭 +1
偙傟偼丆(6N)^3 佭 -1 偲柕弬偡傞偺偱丆晄壜丅
丒r = 2 偺応崌
(6N)^2 佭 +1
p-1 = 6q + 2丆p = 6q + 3
p 偼 5 埲忋偺慺悢偱側偗傟偽側傝傑偣傫偑丆偦偺傛偆側 p 偼懚嵼偟傑偣傫丅
丒r = 3 偺応崌
(6N)^3 佭 +1
偙傟偼丆(6N)^3 佭 -1 偲柕弬偡傞偺偱丆晄壜丅
丒r = 4 偺応崌
(6N)^4 佭 +1
p-1 = 6q + 4丆p = 6q + 5
偦偺堦曽偱丆
(6N)^2 佭 (6N)^2 * (6N)^4 佭 (6N)^6 佭 +1
偮傑傝丆r = 2 偺応崌偵傕婣拝偟偰偟傑偄丆p = 6q +
3 偵傕側傝傑偡丅
偙偺傛偆側 p 偼懚嵼偟傑偣傫丅
丒r = 5 偺応崌
(6N)^5 佭 +1
p-1 = 6q + 5丆p = 6q + 6
p 偼 5 埲忋偺慺悢偱側偗傟偽側傜側偄偺偱丆晄壜丅
寢嬊壜擻側偺偼丆p = 6q + 1 偺応崌偩偗偱偡丅
偮傑傝丆(6N)^3 + 1 偼 6n+1 宆偺慺悢偱妱傝愗傟傑偡丅
偙傟偼丆婛懚偺偳偺 6n+1 宆偺慺悢傕 (6N)^3 + 1
傪妱傝愗傜側偐偭偨偙偲偵柕弬偟傑偡丅
埲忋傛傝丆6n+1 宆偺慺悢偼柍尷屄偁傞偙偲偑偄偊傑偟偨丅
(姶憐)
偙傟偼丆桳柤側丆儐乕僋儕僢僪偵傛傞慺悢偼柍尷屄偁傞偙偲偺徹柧偺椶帡斉偱偡偹丅
桿摫宍幃偵側偭偰偄傞偺偱丆峫偊傗偡偐偭偨偱偡丅
NO2乽kashiwagi乿 11/25 07帪33暘庴怣 峏怴12/13
233夞夝摎
乮1乯
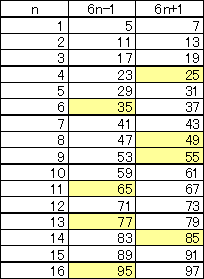
値偺抣偵墳偠偨昞傪嶌惉偡傞偲妋偐偵慺悢偼偙偺2僞僀僾偱昞偝傟傞丅扐偟丄墿怓偱揾傝偮
傇偟偨悢抣偼慺悢偱偼側偄丅
乮2乯忋昞傛傝丄奺乆偺慺悢偼帺傜傪栺悢偵傕偮偺偱忦審傪枮偨偟偰偄傞丅栤戣偼慺悢偱柍偄傕偺偩偑丄35亖5亊7丄65亖5亊13丄77亖7亊11丄95亖5亊19丄119亖7亊17丄161亖7亊23丒丒丒丒偲偄偆傛偆偵6値-1僞僀僾偺慺悢5丄11丄17丄23丒丒丒傪栺悢偵帩偮偙偲偑暘偐傞丅
乮3乯偙偺僞僀僾偺慺悢偑桳尷偩偲偡傞偲丄堦斣戝偒側慺悢偑懚嵼偡傞丅偦偺慺悢傪俙偲偟丄偙偺僞僀僾偺慺悢慡偰偺愊傪俛偲偡傞偲丄
俛亖5亊11亊17亊23亊丒丒丒丒丒丒丒亊俙偲昞偣傞丅偙偙偱丄俛偵1傪壛偊偨悢傪俠偲偡傞偲丄
俠亖5亊11亊17亊23亊丒丒丒丒丒丒丒亊俙亄1偲側傞丅
偙偺俠偼5,11,17丒丒丒丒俙偺偳偺悢偱傕妱傝愗傟偢丄1梋傞丅懄偪丄俠偼偙傟傜慺悢偺栺悢偱偼側偄丅懄偪丄俠偼慺悢偱偁傝丄俛傛傝戝偒側悢偲側傞丅偙傟偼嵟戝偺慺悢偼俙偱偁傞偲偄偆慜採偲柕弬偡傞丅場偭偰丄6値-1僞僀僾偺慺悢偼柍尷偵懚嵼偡傞丅
NO3乽接案陷乿 12/02 22帪59暘庴怣 峏怴12/13
偍媣偟傇傝偱偡 ^^;
崱夞偼庤偑弌偦偆偩偭偨偺偱...僩儔僀偟傑偡 Orz乣
乮侾乯俆埲忋偺慺悢偼丄偁傞帺慠悢値傪傕梡偄偰俇値亄侾傑偨偼俇値亅侾偺宍偵昞偝
傟傞偙偲傪帵偣丅
慺悢傪娷傔偨偁傜備傞5埲忋偺悢偼丄
6n
6n亇1
6n亇2
6n亇3
偺偄偢傟偐偱昞傢偝傟傞...
偑...
慺悢偲偡傞偲...
柧傜偐偵...6n亇1 偺宍偱偟偐偁傝偊側偄丅
乮俀乯俶傪帺慠悢偲偡傞丅俇俶亅侾偼丄俇値乗侾乮値偼帺慠悢乯偺宍偱昞偝傟傞慺悢
傪栺悢偵傕偮偙偲傪帵偣丅
5埲忋偺帺慠悢 6N-1 偼丄(1)偐傜...崌惉悢側傜...偁傜備傞5埲忋偺慺悢偑 6n亇1 偱
昞傢偝傟傞偺偩偐傜...
偦傟傜偺慺悢偺愊偱昞傢偝傟傞丅6n+1 偩偗偺愊偱偼...6N+1
偵側傞偺偱...婏悢屄偺
6n-1
宆偺慺悢傪場巕偵帩偮偙偲偑尵偊傞丅
乮俁乯俇値乗侾乮値偼帺慠悢乯偺宍偱昞偝傟傞慺悢偼柍尷偵懡偔懚嵼偡傞偙偲傪帵偣
丅
桳尷偺m屄偟偐側偄偲偡傞偲...
(6n_1-1)(6n_2-1)丒丒丒(6n_m-1)-1 偲偄偆悢偼...
(2)偐傜...6n-1 偲偄偆慺場悢傪彮側偔偲傕1屄 or 婏悢屄帩偭偰偄傞偼偢偩偑...
偦傟偼丄6n_1-1乣6n_m-1 偺 m屄偺慺悢偱偼側偄偺偱...
怴偟偄慺悢偲偄偆偙偲偵側傝...偙傟偼桳尷偺m屄偟偐側偄偙偲偵柕弬偡傞丅
偮傑傝...6n-1 宆偺慺悢偼柍尷偱偁傞偲偄偊傞丅
儐乕僋儕僢僪偝傫偺慺悢偺柍尷偺徹柧朄偺摜廝偱偡偹...^^;v
崱擭傕僇僂儞僩僟僂儞偲側傝傑偟偨偑丂彮偟憗偄偗偳...傛偄偍擭傪偍寎偊偔偩偝偄
傑偣乣^^
棃擭傕偱偒傞偩偗僠儍儗儞僕偟偨偄偲巚偄傑偡 m(_ _)m兞
傑偨丄傛傠偟偔偍婅偄偄偨偟傑偡乣乣乣侓
亙悈偺棳傟丗乽慺悢偑柍尷偵懚嵼偡傞乿偲偄偆柦戣傪楌巎揑偵桳柤側3恖偺徹柧傪徯夘偟傑偡丅亜
丂柦戣丗慺悢偼柍尷偵懚嵼偡傞丂
嘆丂儐乕僋儕僢僪偵傛傞徹柧丂
攚棟朄偵傛傞丅慺悢偺屄悢偑桳尷屄偱偁偭偨偲偟偰丄偦傟傜傪丄倫侾丆倫俀丆倫俁丆丒丒丒丆倫値丂偲偡傞丅
偙傟傜埲奜偺惍悢偼崌惉悢偱偁傞丅
偙偙偱丄
俶亖倫侾亊倫俀亊倫俁亊丒丒丒亊倫値亄侾丂傪嶌傞丅
偙傟偼傕偪傠傫崌惉悢偩偐傜丄偁傞慺悢偱妱傝愗傟傞偼偢偱偁傞丅
偲偙傠偑偡傋偰偺慺悢偱偁傞倫侾丆倫俀丆
倫俁丆丒丒丒丆倫値偺偳傟偱妱偭偰傕侾偑梋偭偰丄妱傝愗傟側偄丅偙傟偼晄崌棟偱偁傞丅
嘇丂僋儞儅乕偵傛傞徹柧
丂慺悢偑桳尷屄偟偐側偄偲偟偰丄偙傟傜傪丄
丂倫侾丆倫俀丆倫俁丆丒丒丒丆倫値
乮侾亙倫侾亙倫俀亙倫俁亙丒丒丒亙倫値丂乯偲偡傞丅偙傟埲奜偼崌惉悢偱偁傞丅
俶亖倫侾亊倫俀亊倫俁亊丒丒丒亊倫値丂偲偍偔丅俶亅侾偼偳偺倫偲傕堎側傝崌惉悢偩偐傜丄偳傟偐偺慺悢丄椺偊偽倫侾偱妱傝愗傟傞丅俶傕倫侾偱妱傝愗傟傞偐傜丄嵎偺侾偑倫侾偱妱傝愗傟傞偙偲偵側傝丄晄崌棟偱偁傞丅
嘊丂僆僀儔乕偵傛傞徹柧
倫傪擟堄偺慺悢偲偡傞丅
![]() 丂偩偐傜丄柍尷摍斾媺悢偺榓偺岞幃偵傛偭偰丄
丂偩偐傜丄柍尷摍斾媺悢偺榓偺岞幃偵傛偭偰丄
師偺摍幃偑惉傝棫偮丅
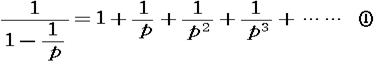
慺悢偑桳尷屄倫侾丆倫俀丆倫俁丆丒丒丒丆倫値丂偱偁偭偨偲偟偰丄奺倫i 偮偄偰嘆傪嶌傝丄偙傟傜傪曈乆妡偗偨幃偺塃曈傪嘇偲偡傞丅
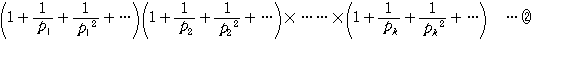
塃曈偺奺媺悢偼愨懳廂懇偩偐傜丄妵屖傪偼偢偟偰暲傋懼偊傕傛偄丅偦偺偲偒偺堦斒崁偺暘曣偼丄
![]()
偺宍偱丄巜悢倎丆倐丆丒丒丒丆們偼丄惓惍悢偺偁傜備傞慻傒崌傢偣傪偲傞丅惍悢偺慺場悢暘夝偺堦堄惈偵傛偭偰丄嘊偵偼偡傋偰偺帺慠悢偑傕傟側偔廳暋側偔尰傟傞偺偱丄嘇偼
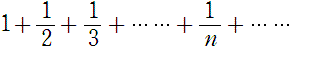
偲側傞偑丄嘆幃傪嶌傝丄偙傟傜傪曈乆妡偗偨幃偺嵍曈偼桳尷屄偺愊偩偐傜桳尷妋掕偱偁傞丅
偙傟偼柕弬丅
丂丂丂
奆偝傫丄摎偊偑傢偐偭偨傜丄堦晹偱傕峔偄傑偣傫偐傜丄夝摎偲儁儞僱乕儉傪揧偊偰丄
儊乕儖偱憲偭偰偔偩偝偄丅懸偭偰偄傑偡丅
![]()
