�����Q�Q�N�P���R��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��Q�R�S�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF12��13���`1��3��
�m�m���͖ʐϔ�i�P�j�n
�F����A�ꍇ�̐��������ɂ���m���̖����l�������Ƃ�����܂����B
�����ŁA���ł��B
���C�����@�������ł���C�ӂɗ^����ꂽ���̐��Ƃ���B�������̐�����ɏ����2�_���Ƃ�Ƃ��C�����Q�_�Ԃ̋�����a�ȏ�ł���m�������߂�B
NO1�uuchinyan�v 12/13 12��24����M �X�V1/3
OB = b �ƂȂ�悤�Ȑ��� OB ���l���܂��B
�����āCOB ��ɓ�_ P�CQ ���COP = x�COQ = y�C0 <= x <= y <= b �ƂȂ�悤�ɂƂ�܂��B
����ƁC���l����̂́CPQ = y - x >= a > 0 �ƂȂ�ꍇ�ł��B
�܂�C0 <= x <= y <= b �ɂ����āCy - x >= a > 0 �ƂȂ�ꍇ�C���l��������ł��B
����́Cx,y ���W�n�Ő}������ƁC
���_�� (0,0), (b,0), (b,b), (0,b) �ƂȂ鐳���`�̍��㔼���̎O�p�`�̂����C
y = x + a �����㑤�̗̈�ł��B
�����̈�ɂ�����_�̕��z�͈�l�ƍl���Ă����̂ŁC���߂�m�� p �́C�����̈�̖ʐϔ�ɂȂ�܂��B
�����ŁC0 < a < b ���l�����āC
p = ((b - a)^2/2)/(b^2/2) = (1 - a/b)^2
�ɂȂ�܂��B
(�l�@)
���ƂɂȂ�̈�� 0 <= x <= y <= b �Ƃ��܂������C0 <= x <= b, 0 <= y <= b �ł��\���܂���B
�����C���̂Ƃ��́C�ΏۂɂȂ�̈悪�C|y - x| >= a > 0 �ƂȂ�܂��B
|y - x| >= a�@
<----->�@((y - x >= 0) and (y - x >= a)) or
((y - x < 0) and (-(y - x) >= a))�@
<----->�@(y >= x + a) or (y <= x - a)
�Ȃ̂ŁC�����l����ƁC
���_�� (0,0), (b,0), (b,b), (0,b) �ƂȂ鐳���`�̂����C
y = x + a �����㑤 ���� y = x - a �������� �̗̈�ł��B
�����ŁC���߂�m���́C
p = ((b - a)^2/2 * 2)/(b^2) = (1 - a/b)^2
�ɂȂ�܂��B
���R�ł����C��قǂ̌��ʂƈ�v���܂��B
�Ȃ��C�\�iBASIC�̃v���O�����Ŋm�F���Ă݂܂����B
�S�̂̃X�P�[���͊m���ɊW���Ȃ��̂� b = 1 �ɂ��Ă��܂��B
RANDOMIZE
LET b = 1
LET n = 1000000
FOR a = 0 TO 1 STEP 0.01
LET c = 0
FOR i = 1 TO n
LET x = RND
LET y = RND
IF ABS(x - y) >= a THEN
LET c = c + 1
END IF
NEXT i
PRINT "a ="; a; "b ="; b
PRINT "���_�l"; (1 - a/b)^2
PRINT "�����l"; c/n
NEXT a
END
a = 0 b = 1
���_�l 1
�����l 1
a = .01 b = 1
���_�l .9801
�����l .97994
a = .02 b = 1
���_�l .9604
�����l .959954
a = .03 b = 1
���_�l .9409
�����l .940893
a = .04 b = 1
���_�l .9216
�����l .921686
a = .05 b = 1
���_�l .9025
�����l .9023
�D�D�D
a = .46 b = 1
���_�l .2916
�����l .291652
a = .47 b = 1
���_�l .2809
�����l .280481
a = .48 b = 1
���_�l .2704
�����l .270639
a = .49 b = 1
���_�l .2601
�����l .259495
a = .5 b = 1
���_�l .25
�����l .249233
a = .51 b = 1
���_�l .2401
�����l .239791
a = .52 b = 1
���_�l .2304
�����l .229517
a = .53 b = 1
���_�l .2209
�����l .220456
a = .54 b = 1
���_�l .2116
�����l .211591
a = .55 b = 1
���_�l .2025
�����l .202725
�D�D�D
a = .96 b = 1
���_�l .0016
�����l .001552
a = .97 b = 1
���_�l .0009
�����l .00089
a = .98 b = 1
���_�l .0004
�����l .000423
a = .99 b = 1
���_�l .0001
�����l .000098
a = 1 b = 1
���_�l 0
�����l 0
���������ƁC�m���ɁC�قڈ�v���Ă��܂��B
(���z)
�m�����ʐϔ�ŕ\�킳��邱�Ƃ����邱�Ƃ́C���K���z�Ȃǂ̃O���t�ł͏펯�Ƃ����Ă������悤�Ɏv���܂��B
�������C���̂悤�Ȗ��Ƃ��Ė����ƁC�ʐH�炤���Ƃ�����܂��ˁB�������K�ɂȂ�܂����B
NO2�u�Ӱ��݁v 12/21 18��20����M �X�V1/3
������`�������W�`^^v
�������F������3���������Ƃ��O�p�`�̂ł���m���́H���Ă̂��݂����Ƃ������
�� ^^
�����...
b-a��a �� b��2a �Ȃ̂�...
a-b���ʂōl�����...
���炩�ɐ����`�� 1/4 �̖ʐϕ����m���ƍl�����܂���ˁH��
�}�Ɋ����������ė��܂���...�\�o���̒l�i���オ���Ă邻���ł�...^^;
�����N�����}�����������܂� �`m(_ _)m�`v
NO3�u���[��v 12/22 10��40����M
�X�V1/3
���u���[�Ă�v����̃R�����g���灄
�����q�������Ă��������Ă���܂��B
��ς��v���Ԃ�ł͂���܂����A���Ă𓊍e�����Ă��������܂��̂ŁA��낵�����肢���܂��B
�ŋ߁A�����ɂ��ł����̂ŁA���t�[�m�b�܂̐��w�◝�Ȃ̎���ɉȂǂ����肵�Ă��܂��B
���܂ɖʔ������₪�����āA�V���Ȑ��w�̐��E�ɏo����Ƃ�����܂��B
�Ⴆ�A
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1433663824
�l������Ԃ̍Ŗ��[�U�ɂ��āA���Ȃ�ɍl���Ă݂܂����B
�������Ă����܂�I�m�Ȃ��Ƃ�������Ă���T�C�g����������Ȃ������̂ŁB
���Ȃ݂ɁAbeetbert�Ƃ����̂����ł��B
���N���A�ʔ��������������肪�Ƃ��������܂����B
���N����낵�����肢���܂��B�ǂ����N���B
�s��@�P�F�L���v�f���̕���������ɂ����Ƃ��̋Ɍ��l�����߂���@�t
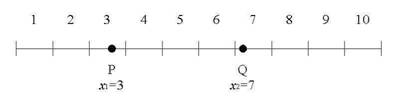
�}�P
�}�P�̂悤�ɁC����10�̐�����10�������C�e��Ԃ̑�\�l��������1, 2, 3, �c10�ƒ�߂�D
������Ƀ����_���ɓ_P�CQ���Ƃ�C�e�_�̑������Ԃ̑�\�l��x1�Cx2 �Ƃ��C���̍���d = |x1-x2|
�Ƃ����D
d=1�ƂȂ�̂́C(x1, x2)=(1,
2), (2, 3), (3, 4), �c, (9, 10), (2, 1), (3, 2), (4, 3), �c, (10, 9) ��2�~9�ʂ�D
d=2�ƂȂ�̂́C(x1, x2)=(1,
3), (2, 4), (3, 5), �c, (8, 10), (3, 1), (4, 2), (5, 3), �c, (10, 8) ��2�~8�ʂ�D
�c�@�ƍl���āCd = k�ƂȂ�̂�2(10-k) �ʂ�ł���D
���������āCd��m�ƂȂ�m�������߂�ƁC![]() �D
�D
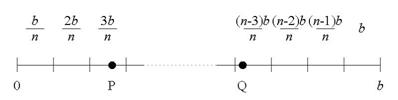
�}�Q
�ȏ���ӂ܂��āC�}�Q�̂悤�ɒ���b�̐�����n�������C�e��Ԃ̑�\�l��������![]() �ƒ�߂�D
�ƒ�߂�D
������ɓ_P�CQ���Ƃ�C�e�_�̑������Ԃ̑�\�l��x1�Cx2 �Ƃ��C���̍���d = |x1-x2|
�Ƃ����D
![]() �Ƃ����Cd��a�ƂȂ�m�������߂�ƁC
�Ƃ����Cd��a�ƂȂ�m�������߂�ƁC
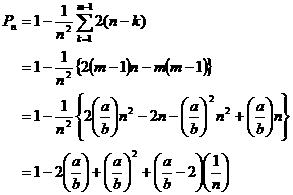
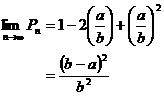
�s��@�Q�F�m�����z����ϕ����ĕ��ϊm�������߂���@�t
����0��x��b��ɂQ�_���Ƃ�D�P�_�ڂ�x = x1 �ł������Ƃ��ɁC�Q�_��x = x2 ���Ƃ��� |x1-x2|��a�ł���m����P(x1) �Ƃ����D
�@b��2a�̏ꍇ
i)0��x1��a�̂Ƃ��C
|x1-x2|��a�ƂȂ�x2 �̂Ƃ蓾��̈�́Cx1+a��x2��b�C�̈�̒����́Cb-a-x1
ii)a��x1��b-a�̂Ƃ��C
|x1-x2|��a�ƂȂ�x2 �̂Ƃ蓾��̈�́C0��x2��x1-a�Cx1+a��x2��b�C�̈�̒����́C(x1-a)+(b-a-x1)=b-2a
iii)b-a��x1��b�̂Ƃ��C
|x1-x2|��a�ƂȂ�x2 �̂Ƃ蓾��̈�́C0��x2��x1-a�C�̈�̒����́Cx1-a
����āC
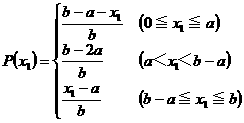
0��x1��b�ɂ�����P(x1) �̕��ϒl�����߂�ƁC
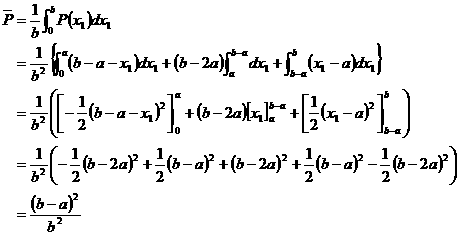
�Aa��b��2a�̏ꍇ
i)0��x1��b-a�̂Ƃ��C|x1-x2|��a�ƂȂ�x2 �̂Ƃ蓾��̈�́Cx1+a��x2��b�C�̈�̒����́Cb-a-x1
ii)b-a��x1��a�̂Ƃ��C|x1-x2|��a����x2�͑��݂��Ȃ��D
iii)a��x1��b�̂Ƃ��C|x1-x2|��a�ƂȂ�x2 �̂Ƃ蓾��̈�́C0��x2��x1-a�C�̈�̒����́Cx1-a
����āC
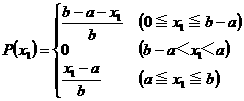
0��x1��b�ɂ�����P(x1)�̕��ϒl�����߂�ƁC
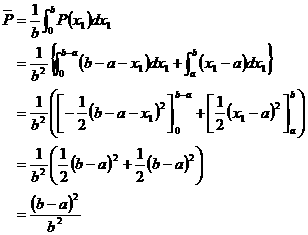
�ȏ���C������̏ꍇ�ɂ��C![]() �D
�D
�s��@�R�F�̈�ɂ���@�t
����0��x��b��ɂQ�_x = x1, x2
���Ƃ�D
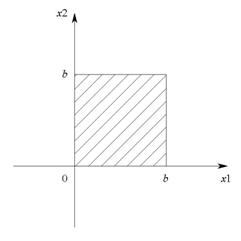
0��x1��b����0��x2��b�Ȃ̂ŁC(x1, x2)�̂Ƃ蓾��̈��x1-x2 �������W�n�ɐ}������ƁC�}�R�Ɏΐ��Ŏ����������`�̓����i�y�ы��E��j�ɂȂ�C(x1, x2)
�͂��̗̈�̑S��ɂ킽���ē������m���ő��݂�����D
�����ŁC������łQ�̋�����a�ȏ�ł�������́C|x1-x2|��a�ƕ\�킹��D
���Ȃ킿�Cx2��x1+a�܂���x2��x1-a�ƂȂ�C�������(x1, x2)
�̂Ƃ蓾��̈��}������ƁC�}�S�Ɏΐ��Ŏ������悤�ɁC���s�ȂQ�����Fx2 = x1-a�Cx2 = x1+a�ɂ͂��܂��̈�̊O���ł��C�}�R�̐����`�̓����̗̈�ɂȂ�D
����āC���߂�m���͐}�R�Ɛ}�S�̊e�̈�̖ʐϔ�ɓ������C![]() �D
�D
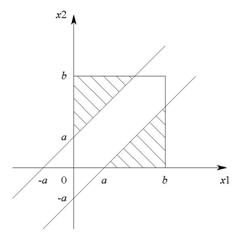
�}�R�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�S
NO4�ukashiwagi�v 12/24 19��54����M
�����̗��ꂩ��̂��l�с���̎��Ԃɉ����傳��܂������A�ꕔ�C�����K�v�ł����B
�N���E�N�n�̊W���牞����Ԓ��ɊԂɍ����܂���ł����̂ŁA����Ȃ��獡�͊��������Ă��炢�܂��B��
�@�@�@
![]()
