�����Q�Q�N�P�P��7��
 [���ꐯ]
[���ꐯ]
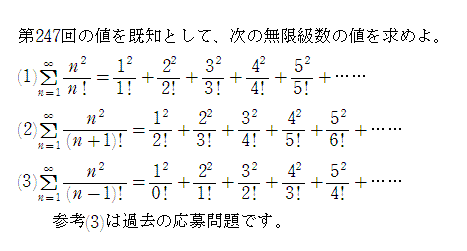
�@�@�@�@�@��Q�S�W�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF10��17���`11��7��
�m���������̔�����(2)�n
����A�y�Џo�Łu��e�̘b�v��ǂ�ł�����A���������̔������ƕs�v�c������
���܂����B�F����ɏЉ�܂��B2��ڂł��B
�@
NO1�uuchinyan�v 10/17 12��19����M
�uuchinyan�v 10/19 17��47����M
�uuchinyan�v 10/22 13��37����M �X�V11/7
��Q�S�W�w�I�ȉ�����
�m���������̔�����(2)�n
��ӂɂ���悤�ɁC������C�ȉ��ł́C
��[n=0,��]{1/n!} = e
��F�߂ċc�_���܂��B
�܂��C���̖��������́C��l��Ύ������邱�Ƃ��m���Ă���̂ŁC
�����̌v�Z�Ȃǂ́C�L�����̉��Z�̏ꍇ�Ɠ����悤�ɂł���O��ŋc�_���܂��B
(1)
��[n=1,��]{n^2/n!}
= ��[n=1,��]{n/(n-1)!}
= ��[n=1,��]{(n-1)/(n-1)! + 1/(n-1)!}
= ��[n=2,��]{1/(n-2)!} + ��[n=1,��]{1/(n-1)!}
= ��[n=0,��]{1/n!} + ��[n=0,��]{1/n!}
= e + e
= 2e
(2)
��[n=1,��]{n^2/(n+1)!}
= ��[n=1,��]{(n^2 - 1)/(n+1)! + 1/(n+1)!}
= ��[n=1,��]{(n-1)(n+1)/(n+1)! + 1/(n+1)!}
= ��[n=1,��]{(n-1)/n! + 1/(n+1)!}
= ��[n=2,��]{(n-1)/n!} + ��[n=2,��]{1/n!}
= ��[n=2,��]{n/n! - 1/n!} + ��[n=2,��]{1/n!}
= ��[n=2,��]{1/(n-1)! - 1/n!} + ��[n=2,��]{1/n!}
= ��[n=2,��]{1/(n-1)!} - ��[n=2,��]{1/n!} + ��[n=2,��]{1/n!}
= ��[n=1,��]{1/n!} - (��[n=0,��]{1/n!}
- 1 - 1) + (��[n=0,��]{1/n!} - 1
- 1)
= ��[n=0,��]{1/n!} - 1 - (e - 2) + (e - 2)
= e - 1
(3)
��[n=1,��]{n^2/(n-1)!}
= ��[n=1,��]{(n^2 - 1)/(n-1)! + 1/(n-1)!}
= ��[n=1,��]{(n-1)(n+1)/(n-1)! + 1/(n-1)!}
= ��[n=1,��]{(n-1)(n+1)/(n-1)!} + ��[n=1,��]{1/(n-1)!}
= ��[n=2,��]{(n+1)/(n-2)!} + ��[n=0,��]{1/n!}
= ��[n=2,��]{(n-2)/(n-2)! + 3/(n-2)!} + ��[n=0,��]{1/n!}
= ��[n=3,��]{1/(n-3)!} + 3 * ��[n=2,��]{1/(n-2)!} + ��[n=0,��]{1/n!}
= ��[n=0,��]{1/n!} + 3 * ��[n=0,��]{1/n!} + ��[n=0,��]{1/n!}
= e + 3e + e
= 5e
(�l�@1)
e^x �̃}�N���[�����W�J�C
��[n=0,��]{x^n/n!} = e^x
���g����D�D�D
(1)
d(��[n=0,��]{x^n/n!})/dx = ��[n=1,��]{n/n! * x^(n-1)}
x * d(��[n=0,��]{x^n/n!})/dx = ��[n=1,��]{n/n! * x^n}
d(x * d(��[n=0,��]{x^n/n!})/dx)/dx = ��[n=1,��]{n^2/n! * x^(n-1)}
���C
��[n=1,��]{n^2/n!}
= [d(x * d(��[n=0,��]{x^n/n!})/dx)/dx]x=1
= [d(x * d(e^x)/dx)/dx]x=1
= [d(x * e^x)/dx]x=1
= [e^x + x * e^x]x=1
= e^1 + 1 * e^1
= e + e
= 2e
(2)
(e^x - 1)/x = (��[n=0,��]{x^n/n!} - 1)/x = ��[n=1,��]{x^(n-1)/n!}
= ��[n=0,��]{x^n/(n+1)!}
d(��[n=0,��]{x^n/(n+1)!})/dx = ��[n=1,��]{n/(n+1)! * x^(n-1)}
x * d(��[n=0,��]{x^n/(n+1)!})/dx = ��[n=1,��]{n/(n+1)! * x^n}
d(x * d(��[n=0,��]{x^n/(n+1)!})/dx)/dx = ��[n=1,��]{n^2/(n+1)! * x^(n-1)}
���C
��[n=1,��]{n^2/(n+1)!}
= [d(x * d(��[n=0,��]{x^n/(n+1)!})/dx)/dx]x=1
= [d(x * d((e^x -
1)/x)/dx)/dx]x=1
= [d(x * (e^x * x - (e^x -
1) * 1)/x^2)/dx]x=1
= [d((e^x * x - e^x +
1))/x)/dx]x=1
= [((e^x * x + e^x - e^x +
0) * x - (e^x * x - e^x + 1) * 1)/x^2]x=1
= [(e^x * x^2 - e^x * x +
e^x - 1)/x^2]x=1
= e^1 * 1^2 - e^1 * 1 + e^1
- 1
= e - e + e - 1
= e - 1
(3)
x * e^x = x * ��[n=0,��]{x^n/n!} = x * ��[n=1,��]{x^(n-1)/(n-1)!}
= ��[n=1,��]{x^n/(n-1)!}
d(��[n=1,��]{x^n/(n-1)!})/dx = ��[n=1,��]{n/(n-1)! * x^(n-1)}
x * d(��[n=1,��]{x^n/(n-1)!})/dx = ��[n=1,��]{n/(n-1)! * x^n}
d(x * d(��[n=1,��]{x^n/(n-1)!})/dx)/dx = ��[n=1,��]{n^2/(n-1)! * x^(n-1)}
���C
��[n=1,��]{n^2/(n-1)!}
= [d(x * d(��[n=1,��]{x^n/(n-1)!})/dx)/dx]x=1
= [d(x * d(x *
e^x)/dx)/dx]x=1
= [d(x * (e^x + x *
e^x)/dx]x=1
= [d((x + x^2) * e^x)/dx]x=1
= [(1 + 2x) * e^x + (x +
x^2) * e^x]x=1
= [(1 + 3x + x^2) * e^x]x=1
= (1 + 3 * 1 + 1^2) * e^1
= (1 + 3 + 1) * e
= 5e
�m���Ɉ�v���Ă��܂��B
(���̗��ꂳ��̃��[���ɂ�锭�W���)
�D�D�D�ŁA�g�����l���Ă��������B
��(k=0�c��)(k+1)/k! = 2e
��(k=0�c��)(k+1)^2/k! = 5e
��������ƁAk = 1 �łȂ��Ak = 0 ����ł����A������
�����܂ł͖��ł������A
���ɁA
��(k=0�c��)(k+1)^3/k! =
��(k=0�c��)(k+1)^4/k! = �@
��(k=0�c��)(k+1)^5/k! =
�D�D�D
�͂ǂ�Ȓl�ɂȂ�ł��傤�B�܂��Ae �̌W���͈�̂ǂ�Ȑ���ł��傤�B
a(n) = ��[k=0,��]{(k+1)^n/k!} �Ƃ����܂��B�������Cn >= 0 �Ƃ��܂��B����ƁC
a(n) = ��[k=0,��]{(k+1)^n/k!}
= ��[k=0,��]{(k+1)^(n+1)/(k+1)!}
= ��[k=1,��]{k^(n+1)/k!}
= ��[k=0,��]{k^(n+1)/k!}
�����ŁCb(n) = ��[k=0,��]{k^n/k!} �Ƃ����ƁC
a(n) = ��[k=0,��]{k^(n+1)/k!} = b(n+1)
�ɂȂ�܂��B���ꂩ��C����̖���
(1) ���Ca(1) = b(2) = 2e
(3) ���Cb(3) = a(2) = 5e
�ɂȂ��Ă��邱�Ƃ�������܂��B�܂��C
b(0) = ��[k=0,��]{1/k!} = e
�ł��B�����āC
b(n+1) = a(n) = ��[k=0,��]{(k+1)^n/k!}
= ��[k=0,��]{��[m=0,n]{nCm * k^m}/k!}
= ��[m=0,n]{nCm * ��[k=0,��]{k^m/k!}}
= ��[m=0,n]{nCm * b(m)}
�Ƃ����Q���������܂�܂��B������C
b(0) = e
a(0) = b(1) = 0C0 * b(0) = 1
* e = e
a(1) = B(2) = 1C0 * b(0) +
1C1 * b(1) = 1 * e + 1 * e = 2e
a(2) = b(3) = 2C0 * b(0) +
2C1 * b(1) + 2C2 * b(2) = 1 * e + 2 * e + 1 * 2e = 5e
a(3) = b(4) = 3C0 * b(0) +
3C1 * b(1) + 3C2 * b(2) + 3C3 * b(3)
= 1 * e + 3 * e + 3 * 2e + 1
* 5e = 15e
a(4) = b(5) = 4C0 * b(0) +
4C1 * b(1) + 4C2 * b(2) + 4C3 * b(3) + 4C4 * b(4)
= 1 * e + 4 * e + 6 * 2e + 4
* 5e + 1 * 15e = 52e
a(5) = b(6) = 5C0 * b(0) +
5C1 * b(1) + 5C2 * b(2) + 5C3 * b(3) + 5C4 * b(4) + 5C5 * b(5)
= 1 * e + 5 * e + 10 * 2e +
10 * 5e + 5 * 15e + 1 * 52e = 203e
�D�D�D
b(n) �� e �̌W������ׂ�ƁC
1, 1, 2, 5, 15, 52, 203, ...
�ƂȂ�܂��B
�Ƃ͂��������̂́C���̐����Ȃ̂��͕����炸�CWeb �Œ��ׂĂ݂���C
�ǂ����C�x�����C�Ƃ������̂ŁC
�@n �̎��R���̏W�����C���̓O���[�v���C������@�̑���
�������ł��B
http://ja.wikipedia.org/wiki/%E3%83%99%E3%83%AB%E6%95%B0
�ɁC�ڂ��Ă��܂����BWeb �͂������I
�����v���ĂӂƁC����́C����������ƁC
�@n �̋�ʂł���{�[���� n �̋�ʂł��Ȃ����ɐU�蕪����ꍇ�̐�
�Ɠ������ȁC�Ǝv������܂����B
����������Ă݂܂��傤�B
�܂��́C�n���Ȍv�Z�B
�En = 1 �̏ꍇ�@���炩�� 1 �ʂ�
�En = 2 �̏ꍇ�@2 �Ƃ���̔��ɓ���Ă��܂�����̔��� 1 ������邩�Ȃ̂� 2 �ʂ�
�En = 3 �̏ꍇ
1 �̔��ɂ��ׂē����@1 �ʂ�
2 �̔��ɕ����ē����@2 �� 1 �ɂȂ�܂����C�ǂ̃{�[���� 1 �ɂ��邩�� 3 �ʂ�
3 �̔��ɕ����ē����@1 �������Ȃ��̂� 1 �ʂ�
���v 1 + 3 + 1 = 5 �ʂ�
�En = 4 �̏ꍇ
1 �̔��ɂ��ׂē����@1 �ʂ�
2 �̔��ɕ����ē����@3 + 1 �� 4C3 = 4 �ʂ�C2 + 2 ��
4C2 * 2C2 * 1/2 = 3 �ʂ�C�� 7 �ʂ�
3 �̔��ɕ����ē����@2 + 1 + 1 �Ȃ̂� 4C2 * 2C1 * 1C1 * 1/2 = 6 �ʂ�
4 �̔��ɕ����ē����@1 + 1 + 1 +
1 �Ȃ̂� 1 �ʂ�
���v 1 + 7 + 6 + 1 = 15 �ʂ�
�En = 5 �̏ꍇ
1 �̔��ɂ��ׂē����@1 �ʂ�
2 �̔��ɕ����ē����@
4 + 1 �� 5C4 = 5 �ʂ�C3 + 2 �� 5C3 * 3C2 = 10 �ʂ�C�� 15 �ʂ�
3 �̔��ɕ����ē����@
3 + 1 + 1 �� 5C3 * 2C1 * 1C1 *
1/2 = 10 �ʂ�C
2 + 2 + 1 �� 5C2 * 3C2 * 1/2 *
1C1 = 15 �ʂ�C
�Ȃ̂ŁC25 �ʂ�
4 �̔��ɕ����ē����@2 + 1 + 1 +
1 �Ȃ̂� 5C2 * 3C1 * 2C1 * 1C1 * 1/3! = 10 �ʂ�
5 �̔��ɕ����ē����@1 + 1 + 1 +
1 + 1 �Ȃ̂� 1 �ʂ�
���v 1 + 15 + 25 + 10 +
1 = 52 �ʂ�
�En = 6 �̏ꍇ
1 �̔��ɂ��ׂē����@1 �ʂ�
2 �̔��ɕ����ē����@
5 + 1 �� 6C5 = 6 �ʂ�C
4 + 2 �� 6C4 * 2C2 = 15 �ʂ�C
3 + 3 �� 6C3 * 3C3 * 1/2 = 10
�ʂ�C
�Ȃ̂� 31 �ʂ�
3 �̔��ɕ����ē����@
4 + 1 + 1 �� 6C4 * 2C1 * 1C1 *
1/2 = 15 �ʂ�C
3 + 2 + 1 �� 6C3 * 3C2 * 1C1 = 60
�ʂ�C
2 + 2 + 2 �� 6C2 * 4C2 * 2C2 *
1/3! = 15 �ʂ�C
�Ȃ̂ŁC90 �ʂ�
4 �̔��ɕ����ē����@
3 + 1 + 1 + 1 �� 6C3 * 3C1 * 2C1 *
1C1 * 1/3! = 20 �ʂ�C
2 + 2 + 1 + 1 �� 6C2 * 4C2 * 1/2 *
2C1 * 1C1 * 1/2 = 45 �ʂ�C
�Ȃ̂ŁC65 �ʂ�
5 �̔��ɕ����ē����C2 + 1 + 1 +
1 + 1 �Ȃ̂� 6C2 * 4C1 * 3C1 * 2C1 * 1C1 * 1/4! = 15 �ʂ�
6 �̔��ɕ����ē����C1 + 1 + 1 +
1 + 1 + 1 �Ȃ̂� 1 �ʂ�
���v 1 + 31 + 90 + 65 +
15 + 1 = 203 �ʂ�
�D�D�D
�m���Ɉ�v���Ă��܂��B
����������ł͐肪�Ȃ��̂ŁC�Q�������l���Ă݂܂��傤�B
n �̋�ʂł���{�[���� n �̋�ʂł��Ȃ����ɐU�蕪����ꍇ�̐��� B(n) �ʂ�Ƃ��܂��B
���炩�� B(1) = 1 �ł��B�܂��C��̕X��CB(0) = 1 �ƒ�`���Ă����܂��B
���āCn+1 �̃{�[���� n+1 �̔�������Ƃ��āC����� 1 �̃{�[���ɒ��ڂ��܂��B
����� A �Ƃ��܂��傤�B
����ƁCA ���܂����ɓ����ƁC����́C���ɋ�ʂ��Ȃ��̂ŁC�ǂ��ɓ���Ă������ł��B
���̏�ԂɎc��� n �̃{�[����lj����܂��B
�E���̃{�[���� A �Ɠ������ɓ���Ȃ��ꍇ
�c��� n �̃{�[���� n �̔��ɐU�蕪����̂� B(n) �ʂ�B
�E���̃{�[�� 1 ������ A �Ɠ������ɓ���ꍇ
�c��� n �̃{�[������ 1 ��I�Ԃ̂� nC1 �ʂ�C
����ȊO�� n-1 �̃{�[���� n �̔��ɐU�蕪����̂ł����C�K�� 1 �̔��͋�ɂȂ�̂ŁC
���ۂ� n-1 �̋�ʂ̂Ȃ����ɐU�蕪���邱�ƂɂȂ�CB(n-1) �ʂ�C
���v�� nC1 * B(n-1) �ʂ�B
�E���̃{�[�� 2 ������ A �Ɠ������ɓ���ꍇ
�c��� n �̃{�[������ 2 ��I�Ԃ̂� nC2 �ʂ�C
����ȊO�� n-2 �̃{�[���� n �̔��ɐU�蕪����̂ł����C�K�� 2 �̔��͋�ɂȂ�̂ŁC
���ۂ� n-2 �̋�ʂ̂Ȃ����ɐU�蕪���邱�ƂɂȂ�CB(n-2) �ʂ�C
���v�� nC2 * B(n-2) �ʂ�B
�ȉ����l�ɍl���āC
�D�D�D
�E���̃{�[�� m ������ A �Ɠ������ɓ���ꍇ
�c��� n �̃{�[������ m ��I�Ԃ̂� nCm �ʂ�C
����ȊO�� n-m �̃{�[���� n-m �̋�ʂ̂Ȃ����ɐU�蕪����̂ŁCB(n-m) �ʂ�C
���v�� nCm * B(n-m) �ʂ�B
�D�D�D
�E���̃{�[�����ׂĂ� A �Ɠ������ɓ���ꍇ
�c��� n �̃{�[������ n ��I�Ԃ̂� nCn �ʂ�C
����ȊO�̐U�蕪���͂Ȃ��̂ł����C�X��CB(n-n)
= B(0) = 1 �ʂ�C�ƍl���āC
���v�� nCn * B(0) �ʂ�B
�ȏ�ł��ׂĂȂ̂ŁCnC0 = 1 �ɒ��ӂ��āC
B(n+1) = ��[m=0.n]{nCm * B(n-m)}
= ��[m=0.n]{nC(n-m) * B(n-m)} = ��[m=0.n]{nCm * B(m)}
�������CB(0) = B(1) = 1 �ł��B
B(n) �̑Q�����ƁCb(n) �̑Q�������ׂ�ƁC�m���ɓ����ŁC�����l�̊W����C
a(n-1) = b(n) = B(n) * e
�ƂȂ��Ă��邱�Ƃ�������܂��B
�ȏ�ŁCb(n) �́C���������� a(n) �́C���̂������܂����B
�������C�Q�����Ƃ��̈Ӗ��͕����������̂́C���̉����ȒP�Ȏ��ŏ��������͓̂�����ł��B
�܂��Ce �ɗ��ޖ����������C�{�[���̐U�蕪�����ƌ��т��Ă���Ƃ́C�s�v�c�Șb�ł��B
(�l�@2)
���W�����l���Ă��āC�{�[���̔��ւ̐U�蕪����肪�o�Ă��܂������C
������Ď��������l�������Ƃ����ȁC�Ǝv���Ă����̂ł����C����Ǝv���o���܂����B
��P�X�T�w�I�ȉ�����C�ł����B�����{��Ƃ͗���܂����C����Ƃ̊W�����Ă����܂��B
�܂��C���W���ł�
�@n �̋�ʂł���{�[���� n �̋�ʂł��Ȃ����ɐU�蕪����ꍇ�̐�
�̒n���Ȍv�Z��U��Ԃ��Č��܂��傤�B����́C���ǁC
�@n �̋�ʂł���{�[���� m �Cm = 1 �` n�C�̋�ʂł��Ȃ�����
�@�����Ȃ��悤�ɐU�蕪����ꍇ�̐��� m
= 1 �` n �ő����グ������
�ɂȂ��Ă��܂��B�����ŁC
�@n �̋�ʂł���{�[���� m �̋�ʂł��Ȃ����ɋ����Ȃ��悤�ɐU�蕪����ꍇ�̐�
�� S(n,m) �ʂ�Ƃ��܂��B����ƁC
B(n) = ��[m=1,n]{S(n,m)}
�Ə����܂��B
�Ȃ��CWeb�Œ��ׂ��Ƃ���C����ɂ͖��O�������āC��Q��̃X�^�[�����O���Ƃ��������ł��B
���āCS(n,m) �́C���̂悤�ɍl����ΑQ���������܂��B
�{�[���� n+1 �C���� m+1 �̏ꍇ���l���C����̃{�[�� A �ɒ��ڂ��܂��B����ƁC
�EA �ȊO�� n �̃{�[���� m �̔��ɋ����Ȃ��悤�ɐU�蕪�� A ���c��̔��ɓ����ꍇ
����́CS(n,m) * 1 =
S(n,m) �ʂ�ł��B
�EA �ȊO�� n �̃{�[���� m+1 �̔��ɋ����Ȃ��悤�ɐU�蕪�� A ���ǂ����̔��ɓ����ꍇ
����́CS(n,m+1) * (m+1)C1
= (m+1) * S(n,m+1) �ʂ�ł��B
���̓�̏ꍇ�����Ȃ��̂ŁC
S(n+1,m+1) = S(n,m) + (m+1)
* S(n.m+1)
�������CS(0,0) = 1�CS(n,0) = 0 for n >= 1�CS(n,m) = 0 for n
< m �Ƃ��Ă����܂��B
�����p����ƁC��قǂ̒n���Ȍv�Z�́C�p�X�J���̐��O�p�`���ɁC
S(1,1) = 1, B(1) = 1
S(2,1) = 1, S(2,2) = 1, B(2)
= 2
S(3,1) = 1, S(3,2) = 3,
S(3,3) = 1, B(3) = 5
S(4,1) = 1, S(4,2) = 7,
S(4,3) = 6, S(4,4) = 1, B(4) = 15
S(5,1) = 1, S(5,2) = 15,
S(5,3) = 25, S(5,4) = 10, S(5,5) = 1, B(5) = 52
S(6,1) = 1, S(6,2) = 31,
S(6,3) = 90, S(6,4) = 65, S(6,5) = 15, S(6,6) = 1, B(6) = 203
�D�D�D
�ƁC�e�ՂɌv�Z�ł��܂��B
���āC���� S(n,m) �ƁC��P�X�T�w�I�ȉ�����Ƃ̊W���l���Ă݂܂��傤�B
��P�X�T��́C���ǂ́C
�@n �̋�ʂł���{�[���� m �̋�ʂł��锠�ɋ����Ȃ��悤�ɐU�蕪����ꍇ�̐�
�����߂���ł��B�������C��P�X�T��ł́Cn
�� m �Ƃ��t�ɂȂ��Ă���_�ɒ��ӁB
S(n,m) �Ɣ�ׂĂ݂�ƁC�Ⴂ�́C������ʂ���_�����ł��B
�����ŁC����� T(n,m) �ʂ�Ƃ���ƁC�e S(n,m) �ɑ��āC���̋�ʂ� m! �ʂ肸����̂ŁC
T(n,m) = S(n,m) * m!
S(n,m) = T(n,m)/m!
�ɂȂ�܂��BT(n,m) �����߂�̂͌��\��ςł����C��P�X�T��̌��ʂ��C
T(n,m) = ��[i=0,m-1]{(-1)^i *
mCi * (m-i)^n}
�����ŁC
S(n,m) = ��[i=0,m-1]{(-1)^i *
mCi * (m-i)^n} * 1/m!
�ɂȂ�܂��B�����C���܂�v�Z���y�Ȍ`�ł͂Ȃ��ł��� (^^; �ꉞ�m�F����ƁC
S(1,1) = (1C0 * 1^1)/1! =
1/1 = 1
S(2,1) = (1C0 * 1^2)/1! =
1/1 = 1
S(2,2) = (2C0 * 2^2 - 2C1 *
1^2)/2! = (4 - 2)/2 = 2/2 = 1
S(3,1) = (1C0 * 1^3)/1! =
1/1 = 1
S(3,2) = (2C0 * 2^3 - 2C1 *
1^3)/2! = (8 - 2)/2 = 6/2 = 3
S(3,3) = (3C0 * 3^3 - 3C1 *
2^3 + 3C2 * 1^3)/3! = (27 - 24 + 3)/6 = 6/6 = 1
S(4,1) = (1C0 * 1^4)/1! =
1/1 = 1
S(4,2) = (2C0 * 2^4 - 2C1 *
1^4)/2! = (16 - 2)/2 = 14/2 = 7
S(4,3) = (3C0 * 3^4 - 3C1 *
2^4 + 3C2 * 1^4)/3! = (81 - 48 + 3)/6 = 36/6 = 6
S(4,4) = (4C0 * 4^4 - 4C1 *
3^4 + 4C2 * 2^4 - 4C3 * 1^4)/4!
= (256 - 324 + 96 - 4)/24 =
24/24 = 1
S(5,1) = (1C0 * 1^5)/1! =
1/1 = 1
S(5,2) = (2C0 * 2^5 - 2C1 *
1^5)/2! = (32 - 2)/2 = 30/2 = 15
S(5,3) = (3C0 * 3^5 - 3C1 *
2^5 + 3C2 * 1^5)/3! = (243 - 96 + 3)/6 = 150/6 = 25
S(5,4) = (4C0 * 4^5 - 4C1 *
3^5 + 4C2 * 2^5 - 4C3 * 1^5)/4!
= (1024 - 972 + 192 - 4)/24
= 240/24 = 10
S(5,5) = (5C0 * 5^5 - 5C1 *
4^5 + 5C2 * 3^5 - 5C3 * 2^5 + 5C4 * 1^5)/5!
= (3125 - 5120 + 2430 - 320
+ 5)/120 = 120/120 = 1
S(6,1) = (1C0 * 1^6)/1! =
1/1 = 1
S(6,2) = (2C0 * 2^6 - 2C1 *
1^4)/2! = (64 - 2)/2 = 32/2 = 31
S(6,3) = (3C0 * 3^6 - 3C1 *
2^6 + 3C2 * 1^6)/3! = (729 - 192 + 3)/6 = 540/6 = 90
S(6,4) = (4C0 * 4^6 - 4C1 *
3^6 + 4C2 * 2^6 - 4C3 * 1^6)/4!
= (4096 - 2916 + 384 - 4)/24
= 1560/24 = 65
S(6,5) = (5C0 * 5^6 - 5C1 *
4^6 + 5C2 * 3^6 - 5C3 * 2^6 + 5C4 * 1^6)/5!
= (15625 - 20480 + 7290 -
640 + 5)/120 = 1800/120 = 15
S(6,6) = (6C0 * 6^6 - 6C1 *
5^6 + 6C2 * 4^6 - 6C3 * 3^6 + 6C4 * 2^6 - 6C5 * 1^1)/6!
= (46656 - 93750 + 61440 -
14580 + 960 - 6)/720 = 720/720 = 1
�D�D�D
�m���Ɉ�v���Ă��܂��B
�����ŁC���p�I���ǂ����͋^��ł����C�ꉞ�C
B(n) = ��[m=1,n]{S(n,m)} = ��[m=1,n]{��[i=0,m-1]{(-1)^i * mCi * (m-i)^n} *
1/m!}
�ɂȂ�܂��ˁB
(�l�@3)
a(n)�Cb(n) �̌v�Z�ɂ́C(�l�@1)�Ŏg���������ɂ��v�Z���\�ł��B
(�l�@1)��(3)�Ɠ��l�ɍl���āC
b(n+1) = a(n) = ��[k=0,��]{(k+1)^n/k!} = [(d/dx * (x * ))^n * (e^x)]x=1
�Ə����܂��B�����ŁC(d/dx * (x *
))^n * ... �́C
�܂� x �������C����� x �Ŕ�������C�Ƃ�������� n ��s�����Ƃ��Ӗ�����C�Ƃ��܂��B
(d/dx * (x * ))^(n+1) * ...
= (d/dx * (x * (d/dx * (x * ))^n * ... ))
��������̂ŁCb(n+1) �̌v�Z�ɂ� b(n) �̌v�Z�̓r���̌��ʂ��g���܂��B
���ۂɌv�Z���Ă݂�ƁC
b(1) = a(0) = [(d/dx * (x *
))^0 * (e^x)]x=1 = [e^x]x=1 = e^1 = e
b(2) = a(1) = [(d/dx * (x *
))^1 * (e^x)]x=1
= [d(x * e^x)/dx]x=1
= [(e^x + x * e^x)]x=1 = [(1
+ x) * e^x]x=1
= (1 + 1) * e^1 = 2e
b(3) = a(2) = [(d/dx * (x *
))^2 * (e^x)]x=1
= [d(x * ((d/dx * (x * ))^1
* (e^x)))/dx]x=1
= [d(x * ((1 + x) *
e^x))/dx]x=1
= [d((x + x^2) * e^x)/dx]x=1
= [((1 + 2x) * e^x + (x + x^2)
* e^x)]x=1 = [(1 + 3x + x^2) * e^x]x=1
= (1 + 3 + 1) * e^1 = 5e
b(4) = a(3) = [(d/dx * (x *
))^3 * (e^x)]x=1
= [d(x * ((d/dx * (x * ))^2
* (e^x)))/dx]x=1
= [d(x * ((1 + 3x + x^2) *
e^x))/dx]x=1
= [d((x + 3x^2 + x^3) *
e^x)/dx]x=1
= [((1 + 6x + 3x^2) * e^x +
(x + 3x^2 + x^3) * e^x)]x=1
= [(1 + 7x + 6x^2 + x^3) *
e^x]x=1
= (1 + 7 + 6 + 1) * e^1 =
15e
b(5) = a(4) = [(d/dx * (x *
))^4 * (e^x)]x=1
= [d(x * ((d/dx * (x * ))^3
* (e^x)))/dx]x=1
= [d(x * ((1 + 7x + 6x^2 +
x^3) * e^x))/dx]x=1
= [d((x + 7x^2 + 6x^3 + x^4)
* e^x)/dx]x=1
= [((1 + 14x + 18x^2 + 4x^3)
* e^x + (x + 7x^2 + 6x^3 + x^4) * e^x)]x=1
= [(1 + 15x + 25x^2 + 10x^3
+ x^4) * e^x]x=1
= (1 + 15 + 25 + 10 + 1) *
e^1 = 52e
b(6) = a(5) = [(d/dx * (x *
))^5 * (e^x)]x=1
= [d(x * ((d/dx * (x * ))^4
* (e^x)))/dx]x=1
= [d(x * ((1 + 15x + 25x^2 +
10x^3 + x^4) * e^x))/dx]x=1
= [d((x + 15x^2 + 25x^3 +
10x^4 + x^5) * e^x)/dx]x=1
= [((1 + 30x + 75x^2 + 40x^3
+ 5x^4) * e^x + (x + 15x^2 + 25x^3 + 10x^4 + x^5) * e^x)]x=1
= [(1 + 31x + 90x^2 + 65x^3
+ 15x^4 + x^5) * e^x]x=1
= (1 + 31 + 90 + 65 + 15 +
1) * e^1 = 203e
�D�D�D
�m���Ɉ�v���Ă��܂��B
�������C�v�Z�Ɍ���� x �̑������̌W���́C��Q��̃X�^�[�����O���CS(n,m) �ɂȂ��Ă��܂��B
����́Cb(n) = a(n-1) �Ō���� x �̑������́C
n >= 1 �� ��[m=0,n-1]{s(n,m+1)
* x^m} �Ƃ����āCc(n,m) = 0 for n < m �������Ă��āC
b(0) = e ���Cs(0,0) = 1�C�ł��B
�����ŁCs(n,m+1) �Ƃ����ݒ肪�ꌩ��ł����CS(n,m) �Ɣ�r����ꍇ�C
S(n,m) �ł� m = 1 �` n �ł����C�������̕��� m = 0 �` n-1 �Ƃ���Ă���̂ŁC
�Ή������₷�����邽�߂ɁC�����āC���������Ă��܂��B
�����ŁCn �� 0 �̂Ƃ��� s(n,0) = 0 �Ƃ��Ă����܂��B
���āC���̑����� * e^x �� ((d/dx * (x * )) ���s���ƁB
((d/dx * (x * ))((��[m=0,n-1]{s(n,m+1) *
x^m}) * e^x)
= (d/dx)((��[m=0,n]{s(n,m+1) *
x^(m+1)}) * e^x)
= (��[m=0,n-1]{s(n,m+1) *
(m+1) * x^m}) * e^x + (��[m=0,n-1]{s(n,m+1) * x^(m+1)})
* e^x
= (��[m=0,n-1]{s(n,m+1) *
(m+1) * x^m}) * e^x + (��[m=1,n]{s(n,m) * x^m}) * e^x
= (��[m=0,n]{(s(n,m) +
s(n,m+1) * (m+1)) * x^m}) * e^x
���ꂪ�Cb(n+1) = a(n) �Ɍ���鑽�����Ɠ������̂ŁC
= (��[m=0,n]{s(n+1,m+1) *
x^m}) * e^x
�����ŁC
s(n+1,m+1) = s(n,m) + (m+1)
* s(n,m+1)
����́CS(n,m) �̑Q����
S(n+1,m+1) = S(n,m) + (m+1)
* S(n.m+1)
�ƈ�v���܂��B�����l����v���Ă���̂ŁC�m���ɁCs(n,m) = S(n,m) �ɂȂ�܂��B
�����ɂ��v�Z�Ɋւ��ẮC
d((e^x)^k)/dx = d(e^(kx))/dx
= k * e^(kx) = k * (e^x)^k
�ɒ��ӂ���ƁC
a(n-1) = b(n) = ��[k=0,��]{k^n/k!}
= [��[k=0,��]{(k^n * (e^x)^k)/k!}]x=0
= [(d/dx)^n * (��[k=0,��]{(e^x)^k/k!})]x=0
= [(d/dx)^n * (e^(e^x))]x=0
�Ƃ������܂��B�����ŁCf(x) =
e^(e^x) ���}�N���[�����W�J����ƁC
e^(e^x) = f(x) = ��[k=0,��]{f^{k}(0)/k! * x^k}
f^{k}(0) = [(d/dx)^k *
(e^(e^x))]x=0
�Ə�����̂ŁCa(n-1) = b(n) �́Ce^(e^x) ���w���^����ƌ����Ƃ��̌W���ɂȂ��Ă��܂��B
���ہC
b(0) = [(d/dx)^0 *
(e^(e^x))]x=0 = [e^(e^x)]x=0 = e
a(0) = b(1) = [(d/dx)^1 *
(e^(e^x))]x=0
= [d(e^(e^x))/dx]x=0 =
[e^(e^x) * e^x]x=0 = e
a(1) = b(2) = [(d/dx)^2 *
(e^(e^x))]x=0
= [d(e^(e^x) * e^x)/dx]x=0
= [e^(e^x) * e^(2x) +
e^(e^x) * e^x]x=0
= [e^(e^x) * (e^x +
e^(2x))]x=0
= e * (1 + 1) = 2e
a(2) = b(3) = [(d/dx)^3 *
(e^(e^x))]x=0
= [d(e^(e^x) * (e^x + e^(2x)))/dx]x=0
= [e^(e^x) * e^x * (e^x +
e^(2x)) + e^(e^x) * (e^x + 2e^(2x))]x=0
= [e^(e^x) * (e^x + 3e^(2x)
+ e^(3x))]x=0
= e * (1 + 3 + 1) = 5e
a(3) = b(4) = [(d/dx)^4 *
(e^(e^x))]x=0
= [d(e^(e^x) * (e^x +
3e^(2x) + e^(3x)))/dx]x=0
= [e^(e^x) * e^x * (e^x +
3e^(2x) + e^(3x))
+ e^(e^x) * (e^x + 6e^(2x) +
3e^(3x))]x=0
= [e^(e^x) * (e^x + 7e^(2x)
+ 6e^(3x) + e^(4x))]x=0
= e * (1 + 7 + 6 + 1) = 15e
a(4) = b(5) = [(d/dx)^5 *
(e^(e^x))]x=0
= [d(e^(e^x) * (e^x +
7e^(2x) + 6e^(3x) + e^(4x)))/dx]x=0
= [e^(e^x) * e^x * (e^x +
7e^(2x) + 6e^(3x) + e^(4x))
+ e^(e^x) * (e^x + 14e^(2x)
+ 18e^(3x) + 4e^(4x))]x=0
= [e^(e^x) * (e^x + 15e^(2x)
+ 25e^(3x) + 10e^(4x) + e^(5x))]x=0
= e * (1 + 15 + 25 + 10 + 1)
= 52e
a(5) = b(6) = [(d/dx)^6 *
(e^(e^x))]x=0
= [d(e^(e^x) * (e^x +
15e^(2x) + 25e^(3x) + 10e^(4x) + e^(5x)))/dx]x=0
= [e^(e^x) * e^x * (e^x +
15e^(2x) + 25e^(3x) + 10e^(4x) + e^(5x))
+ e^(e^x) * (e^x + 30e^(2x)
+ 75e^(3x) + 40e^(4x) + 5e^(5x))]x=0
= [e^(e^x) * (e^x + 31e^(2x)
+ 90e^(3x) + 65e^(4x) + 15e^(5x) + e^(6x))]x=0
= e * (1 + 31 + 90 + 65 + 15
+ 1) = 203e
�D�D�D
�m���Ɉ�v���Ă��܂��B
�������C�v�Z�ɑ�Q��̃X�^�[�����O���CS(n,m)�C������܂����C
(e^(kx))' = k * e^(kx) �� ((d/dx * (x * ) * �Ƃ��C�v�Z�Ƃ��Ă͂قƂ�Ǔ����Ȃ̂ŁC
����́C���炩�ł��傤�B
�Ȃ��CB(n) = b(n)/e �Ȃ̂ŁC���̂��Ƃ���C
e^(e^x - 1) ���x�����̎w���^����ɂȂ��Ă��邱�Ƃ�������܂��B
(�l�@4)
���܂ł̋c�_�ŁC����̖���(1)��(3)�͑啪�l�q�����߂܂������C(2)�͂ǂ��ł��傤���H
�����ŁCc(n) = ��[k=1,��]{k^n/(k+1)!} �Ƃ��ď������ׂĂ݂܂��傤�B
c(0) = ��[k=1,��]{1/(k+1)!} = ��[k=2,��]{1/k!} = ��[k=0,��]{1/k!}
- 1 - 1 = e - 2
n >= 1 �̂Ƃ��́C
c(n) = ��[k=1,��]{k^n/(k+1)!}
= ��[k=0,��]{k^n/(k+1)!}
= ��[k=1,��]{(k-1)^n/k!}
= ��[k=1,��]{��[j=0,n]{(-1)^j * nCj * k^(n-j)}/k!}
= ��[j=0,n]{(-1)^j * nCj
* ��[k=1,��]{k^(n-j)/k!}}
= ��[j=0,n-1]{(-1)^j *
nCj * ��[k=1,��]{k^(n-j)/k!}} +
(-1)^n * ��[k=1,��]{1/k!}
= ��[j=0,n-1]{(-1)^j *
nCj * ��[k=0,��]{k^(n-j)/k!}} +
(-1)^n * (��[k=0,��]{1/k!} - 1)
= ��[j=0,n]{(-1)^j * nCj
* ��[k=0,��]{k^(n-j)/k!}} +
(-1)^(n+1)
= ��[j=0,n]{(-1)^j * nCj
* b(n-j)} + (-1)^(n+1)
�ƂȂ��āCc(n) �� b(n) �ŏ������Ƃ��ł��܂��B�v�Z���Ă݂�ƁC
c(1) = 1C0 * b(1) - 1C1 *
b(0) + 1 = 1 * e - 1 * e + 1 = 1
c(2) = 2C0 * b(2) - 2C1 * b(1)
+ 2C2 * b(0) - 1
= 1 * 2e - 2 * e + 1 * e - 1
= e - 1
c(3) = 3C0 * b(3) - 3C1 *
b(2) + 3C2 * b(1) - 3C3 * b(0) + 1
= 1 * 5e - 3 * 2e + 3 * e -
1 * e + 1 = e + 1
c(4) = 4C0 * b(4) - 4C1 *
b(3) + 4C2 * b(2) - 4C3 * b(1) + 4C4 * b(0) - 1
= 1 * 15e - 4 * 5e + 6 * 2e
- 4 * e + 1 * e - 1 = 4e - 1
c(5) = 5C0 * b(5) - 5C1 *
b(4) + 5C2 * b(3) - 5C3 * b(2) + 5C4 * b(1) - 5C5 * b(0) + 1
= 1 * 52e - 5 * 15e + 10 *
5e - 10 * 2e + 5 * e - 1 * e + 1 = 11e + 1
c(6) = 6C0 * b(6) - 6C1 *
b(5) + 6C2 * b(4) - 6C3 * b(3) + 6C4 * b(2) - 6C5 * b(1) + 6C6 * b(0) - 1
= 1 * 203e - 6 * 52e + 15 *
15e - 20 * 5e + 15 * 2e - 6 * e + 1 * e - 1 = 41e - 1
�D�D�D
�ƂȂ�܂��B�����C�c�O�Ȃ���C����ɉ����Ӗ�������̂��͕������Ă��܂���B
�Ȃ��C���܂ł̋c�_�ŁC
b(j+1) = B(j+1) * e = ��[m=0.j]{jCm * B(m)} *
e = ��[m=0.j]{jCm * b(m)}
b(j) = B(j) * e = ��[m=1,j]{��[i=0,m-1]{(-1)^i * mCi * (m-i)^j} * 1/m!} * e
�Ə�����̂ŁC�������g���Ɖ��������邩���m��܂��C�������Ă��܂���B
(���z)
����̍ŏ��̖�莩�̂́C�O������Ղ��������悤�Ɏv���܂��B
���낢��Ȍv�Z���@������Ǝv���܂����C��芸�����C�v���t�������@�ł���Ă݂܂����B
�Ȃ��C(1)��(3)�ɊW���鐅�̗��ꂳ��̃��[���ɂ�锭�W�����lj����܂����B
�c�O�Ȃ���C�ȒP�Ȏ��ŏ����������Ƃ͂ł��܂���ł������C�l�̋����[���Ӗ��t�����ł��܂����B
���[���C�܂��C�s�v�c�ł��ˁD�D�D
����C(2)�̕��́C(1)�ƊW�����邱�Ƃ͕�����܂������C���̐��̂͂悭�������Ă��܂���B
��������̂��Ȃ��D�D�D
NO2�u�Ӱ��݁v1 10/18 18��15����M
�X�V11/7
����͂Ȃ�Ƃ��ł����C������...^^...?
(2) n^2/(n+1)!={(n^2-1)+1}/(n+1)!
=(n-1)/n!+1/(n+1)!
=1/(n-1)!+1/(n+1)!-1/n!
�@�@1/1+1/2!-1/1!
�@ 1/1!+1/3!-1/2!
�@ 1/2!+1/4!-1/3!
�@�@...
�@�@1/1!+1/2!+1/3!+...=e-1
�ł����̂���...^^v?
�u�Ӱ��݁v2 10/20 16��44����M
�X�V11/7
(1) n^2/n!=n/(n-1)!
=1/(n-2)!+1/(n-1)!
�@ n��2...�^���̑�P����...e
�@ ��Q����n��1�̂Ƃ�...e
�@�@�܂�...2e
���Ă��Ƃ���...?
�@
(3) n^2/(n-1)!={(n^2-1)+1}/(n-1)!
=(n+1)/(n-2)!+1/(n-1)!
=(n-2+3)/(n-2)!+1/(n-1)!
=1/(n-3)!+3/(n-2)!+1/(n-1)!...��Ɠ��l�ɍl�����...�S
�Ă̍���...e�ɂȂ�̂�...
=e+3e+e
=5e
�ł����̂���...^^v?
NO3�u���[��v 11/04 15��44����M
�X�V11/7
�i�P�j
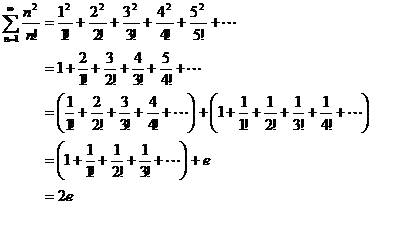
�i�Q�j
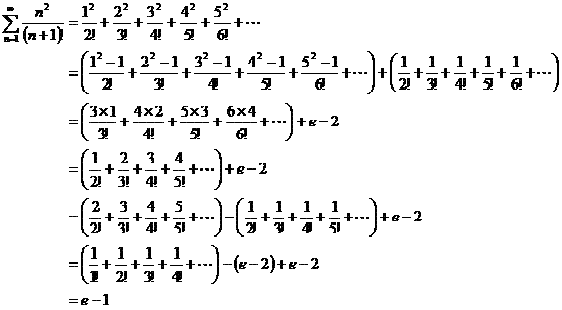
�i�R�j
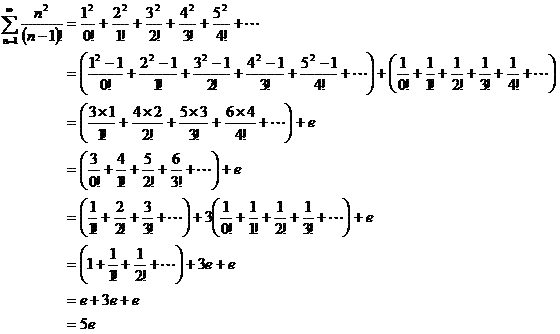
���Ȃ݂ɁA�i�R�j��肽�����ɁA
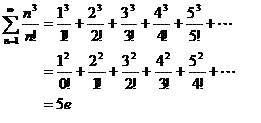
�܂�A
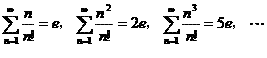
���̐�͎��̌v�Z����ςɂȂ�̂ŃG�N�Z���Ōv�Z�����Ƃ���Ae�̌W���́A
{1�C2�C5�C15�C52�C203�C877�C4,140�C21,147�C115,975
�c}�@�ƂȂ�܂����B
��ʍ���ސ����Ă݂悤�Ǝv���܂�����������܂���ł����B�J�^�������Ƃ��Ⴄ�悤�ł����B
�����̗���F�c�O�ł����A�J�^�������ł͂���܂���B���\�L���Ȑ���ŁA�l�̖��O�����Ă��܂���B��
NO4�uMVH�v 11/06 15��42����M �X�V11/7

���S�̂̃R�����g�F���̖��i�R�j�̊g�����������46��ɂ���܂��B ���Q�l�ɂ��Ă��������B��
�F����A�������킩������A�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA
���[���ő����Ă��������B�҂��Ă��܂��B
