�����Q�R�N�U���P�Q��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��Q�T�W�����w�I�ȉ������
�@�@�@�@�@�@����W���ԁF5��15���`6��12��
�m���n
�u��w�ւ̐��w�v�̃V���[�g�v���O������ǂ�ł�����ʔ�����肪����܂����B
�Љ�܂��B
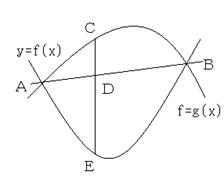
���P�F�̌W�������ꂼ��Q�A�|�P�̂Q�����̃O���t�����}�̂悤�ɂ��ꂼ��
�������i���j�A�������i���j�Ƃ���B�}�łb�c�d�͂����ɕ��s�Ȑ����Ƃ���
�Ƃ��A�b�c�F�c�d������߂�B
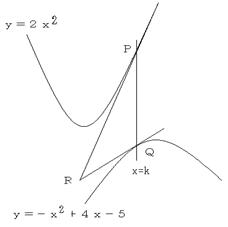
���Q�F���}�ŁA�����Q���Q����@�@�����|���Q�{�S���|�T�E�E�E�A�ƒ����������̌�_��
�o�C�p�Ƃ���B�o�ɂ�����@�̐ڐ��Ƃp�ɂ�����A�̐ڐ��̌�_���q�Ƃ���Ƃ��A
�q�̋O�Ղ̕����������߂�B�������A�O�Ղ̌��E�͋��߂Ȃ��ėǂ��B
�@�@�@
�m�n�P�uuchinyan�v 05/15 16��29����M
�uuchinyan�v 05/16 13��55����M
�X�V6/12
������ʓI�ɉ����Ă����܂��傤�B
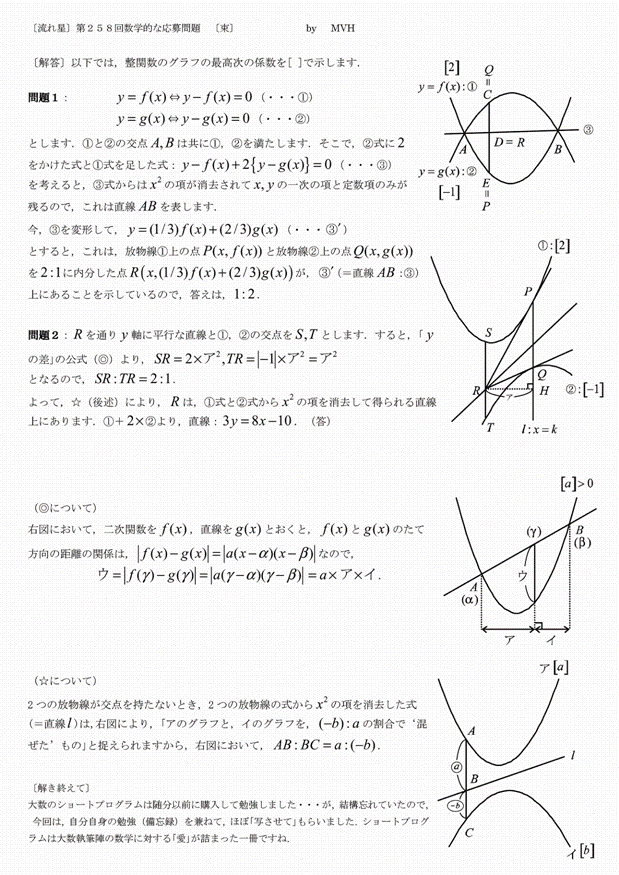
���1�F
��ӂ����܂��������܂��ł����C�}�̏��炵�āC
y = f(x) �� y = g(x) ���CA�CB �Ƃ�����̌�_�����ꍇ���l���邱�Ƃɂ��܂��B
���̂Ƃ��C��_�ł�
f(x) = g(x) �ł����C����͓������œ�����������������ƂɂȂ�C
��_�́CA(��,f(��))�CB(��,f(��))�C�������Cf(��) = g(��)�Cf(��) = g(��)�C�ł��B
����ƁCf(x)�Cg(x) �̓̌W���� a�C-b�Ca�Cb �͐��̎����C�Ƃ��āC
AB �̎��́Cf(x) ��
g(x) �������鎟�̎��ɂȂ�܂��B
y = (b * f(x) +
a * g(x))/(a + b)
���ہC���̎��͓̍����L�����Z������̂ňꎟ���ŁC
x = �� �̂Ƃ��Cy = (b * f(��) + a * g(��))/(a +
b) = ((b + a) * f(��))/(a + b) = f(��)
x = �� �̂Ƃ��Cy = (b * f(��) + a * g(��))/(a +
b) = ((b + a) * f(��))/(a + b) = f(��)
�ƂȂ�C�m���ɁCA�CB ��ʂ�܂��B
������C��
< x = k < �� �Ƃ��āCg(k) > f(k) �Ȃ̂ŁC
C(k,g(k))�CD(k,(b * f(k) + a * g(k))/(a +
b))�CE(k,f(k))
CD = g(k) - (b
* f(k) + a * g(k))/(a + b) = (g(k) - f(k)) * b/(a + b)
DE = (b * f(k)
+ a * g(k))/(a + b) - f(k) = (g(k) - f(k)) * a/(a + b)
CD�FDE = ((g(k) - f(k)) * b/(a + b))�F((g(k) - f(k)) * a/(a + b)) = b�Fa
�ɂȂ�܂��B�܂�CD �� CE �� b�Fa �ɓ�������_�ł��B
���̖��ł́Ca
= 2�Cb = 1 �Ȃ̂ŁCCD�FDE = 1�F2 �ł��ˁB
(�l�@1)
���1�F�ɂ����āCb < 0 �ł��C��_�������ꍇ�ɂ� b �� -a �Ȃ̂ŁCAB �̎��͓����ł��B
�����ŁC��͂�CC(k,g(k))�CD(k,(b * f(k) + a * g(k))/(a + b))�CE(k,f(k))
�Ƃ����܂��B
�������Ca
> |b| �Ȃ�C�ォ�� D�CC�CE �ɂȂ�C�� < x = k < �� �Ƃ��āCg(k) > f(k) �ŁC
CD = (b * f(k)
+ a * g(k))/(a + b) - g(k) = (g(k) - f(k)) * (-b)/(a + b)
DE = (b * f(k)
+ a * g(k))/(a + b) - f(k) = (g(k) - f(k)) * a/(a + b)
CD�FDE = ((g(k) - f(k)) * (-b)/(a +
b))�F((g(k) - f(k)) * a/(a + b)) = (-b)�Fa
�ɂȂ�܂��B
����́CD �� CE �� (-b)�Fa �ɊO������_�ɂȂ��Ă��邱�Ƃ��Ӗ����Ă��܂��B
���l�Ȃ��Ƃ́C0
< a < |b| �� a < 0 �̏ꍇ�ɂ������܂��B
���2�F
y = f(x) = 2x^2�Cy = g(x) = - x^2 + 4x - 5 �Ƃ��܂��B
P(k,f(k)) �ɂ�����ڐ��̎��́Cy = f'(k) * x + (f(k) -
k * f'(k))
Q(k,g(k)) �ɂ�����ڐ��̎��́Cy = g'(k) * x + (g(k) -
k * g'(k))
�����ŁC��_
R(x,y) �́C
f'(k) = g'(k) �̂Ƃ��͕��s�ɂȂ��Č�_�͂Ȃ��̂ŁCf'(k) �� g'(k) �͈̔͂ŁC
f'(k) * x +
(f(k) - k * f'(k)) = g'(k) * x + (g(k) - k * g'(k))
x = k - (f(k) -
g(k))/(f'(k) - g'(k))
y = (f'(k)g(k)
- f(k)g'(k))/(f'(k) - g'(k))
��̓I�ɂ́Ck ��
2/3 �ŁC
x = k - (3k^2 -
4k + 5)/(6k - 4) = (3k^2 - 5)/2(3k - 2)
y = ((- 4k^3 +
16k^2 - 20k) - (- 4k^3 + 8k^2))/(6k - 4) = (4k^2 - 10k)/(3k - 2)
����炩�� k ��������������ł��B
2(3k - 2)x =
3k^2 - 5�C3k^2 - 6xk +
(4x - 5) = 0
(3k - 2)y =
4k^2 - 10k�C4k^2 - (3y
+ 10)k + 2y = 0
�����ŁC
(24x - 9y -
30)k - (16x - 6y - 20) = 0
(8x - 3y -
10)(3k - 2) = 0
�����ŁCk ��
2/3 �������̂ŁC
8x - 3y - 10 =
0
�ɂȂ�܂��B�܂�C���ꂪ R(x,y) �̋O�Ղ̕������ɂȂ�܂��B
����́C���̓�̓��̓̍��������������ɂȂ��Ă��܂��I
�Ȃ��Ck �͎����Ȃ̂ŁCx�Cy �̎��� k �̓�����
3k^2 - 6xk +
(4x - 5) = 0
4k^2 - (3y +
10)k + 2y = 0
�ƌ����Ƃ��C���ꂼ��̔��ʎ��������� 0 ���K�v�ł����C
9x^2 - 3(4x -
5) = (3x - 2)^2 + 11�C����͏�ɐ�
(3y + 10)^2 -
32y = 9y^2 + 28y + 100 = 9(y + 14/9)^2 + 704/9�C����͏�ɐ�
�Ȃ̂ŁC�����͂��Ȃ��Ǝv���܂��B
(k -> 2/3 �� R �͖����̔ޕ��̓_�ɂȂ�܂��B)
(�l�@2)
���2�F����ʓI�ɍl���Ă݂܂��B
��ʂɂ́Cy =
f(x) = a(x - p)^2 + q�Ca �� 0 �łȂ������Cp�Cq �͎����C�Ə�����ꍇ�C
���_ (p,q) �����_ (0,0) �ƂȂ�悤�ɍ��W���s�ړ�����C
��ɁC��̓��́Ca�Cb �� 0 �łȂ������Cc�Cd �������C�Ƃ��āC
y = f(x) = ax^2�Cy = g(x) = bx^2 + cx + d
�Ə����܂��B�}�`�I�Ȑ����͍��W���̕��s�ړ��ŕω����Ȃ��̂ŁC���̏ꍇ���l����Ώ\���ł��B
���āC��_�����݂��邽�߂ɂ́Cf'(x) �� g'(x) ���������Ȃ��Ă͂����Ȃ��̂ŁC
(1) a = b ���� c �� 0
(2) a �� b ���� k �� c/2(a - b)
�ł��B�����C�����͂܂Ƃ߂ċc�_���ł��āC
x = ((a - b)k^2
+ d)/(2(a - b)k - c)
y = (ack^2 +
2adk)/(2(a - b)k - c)
(2(a - b)k -
c)x = (a - b)k^2 + d
(2(a - b)k -
c)y = ack^2 + 2adk
(2(a - b)k -
c)(acx - (a - b)y) = acd - 2ad(a - b)k = - ad(2(a - b)k - c)
(2(a - b)k -
c)(acx - (a - b)y + ad) = 0
(1)�ł� c �� 0�C(2)�ł� k �� c/2(a - b)�C���CR(x,y) �̋O�Ղ̕������́C
acx - (a - b)y
+ ad = 0
�Ƃ��������ɂȂ�܂��B������C��̓�����̍��������������ɂȂ��Ă��܂��I
���̂��Ƃ́C���W���̕��s�ړ������ɖ߂��Ă��C�����͒����ŁC�̍����ς��Ȃ��̂ŁC�p����C
���߂�O�Ղ́C��̓�����̍����������������̎��ɂȂ�܂��I
(�������C���̌W���͕ς��̂ŁC�}�̈ʒu�W�͓����ł��C�����ڂ͕ʂ̒����ɂȂ�܂��B)
���ɑ��ݔ͈͂ł����D�D�D
(1) a = b ���� c �� 0
x = - d/c
y = - (ack^2 +
2adk)/c = - a(k + d/c)^2 + a(d/c)^2
�O�Ղ̒����� x
= - d/c �ł����C
a > 0 �Ȃ� y <= a(d/c)^2�Ca < 0 �Ȃ� y >= a(d/c)^2 �͈̔͂ɂȂ�܂��B
(- d/c,
a(d/c)^2) �͓�̓��C�������C�̌�_�C���̏ꍇ�͌�_�͈�C�Ȃ̂ŁC
�O�Ղ́C��_��ʂ�Ώ̎��ɕ��s�Ȓ����ŁC��_���܂ݕ������̓ʂ��O���̕����C
�Ƃ������ƂɂȂ�܂��B
(2) a �� b ���� k �� c/2(a - b)
a �� b �Ȃ̂ŁCx�Cy �̎��� k �̓�����
(a - b)k^2 -
2(a - b)xk + (cx + d) = 0
ack^2 - 2((a -
b)y - ad)k + cy = 0
�ƌ��邱�Ƃ��ł��Ck
�͎����Ȃ̂ŁC���ꂼ��̔��ʎ��������� 0 ���K�v�ŁC
(a - b)^2 * x^2
- (a - b)(cx + d) >= 0�C((a - b)y - ad)^2 - (ac)(cy) >= 0
�ƂȂ�܂��B�܂�C
(a - b) * ((a -
b)x^2 - cx - d) >= 0
�y�� acx -
(a - b)y + ad = 0 �̉��ŁC
(a - b)^2 * y^2
- a(2(a - b)d + c^2)y + (ad)^2 >= 0
���������ƂɂȂ�܂��By �̎��́Cy = a(cx + d)/(a - b) �Ȃ̂ŁC
(a(cx + d))^2 -
a(2ad(cx + d) + ac^2(cx + d)/(a - b)) + (ad)^2 >= 0
(cx + d)^2 -
(2d(cx + d) + c^2(cx + d)/(a - b)) + d^2 >= 0
c^2/(a - b) *
((a - b)x^2 - cx - d) >= 0
c^2 * (a - b) *
((a - b)x^2 - cx - d) >= 0
����́Cc = 0
�ł͏�ɐ������Cc �� 0 �ł� c^2 > 0 �Ȃ̂ŁC��قǂ� x �̎��Ɉ�v���܂��B
�����ŁC��قǂ�
x �̎�
(a - b) * ((a -
b)x^2 - cx - d) >= 0
�����������������ƂɂȂ�܂��B
(2-1) a > b �̏ꍇ
(a - b)x^2 - cx
- d >= 0
���̎��̍��ӂ́Cax^2
- (bx^2 + cx + d) �ƕό`�ł��C
= 0 �Ƃ������Ƃ��� x �́C��̓��̋��L�_�� x ���W�ɂȂ��Ă��܂��B
�܂��Cx^2 �̌W�� a - b > 0 �ɒ��ӂ��܂��B
(2-1-1) c^2
< 4(a - b)d �̏ꍇ�C��̓������L�_�������Ȃ��ꍇ
x �́C���ׂĂ̒l�����܂��B
(2-1-2) c^2
>= 4(a - b)d �̏ꍇ�C��̓������L�_�����ꍇ
x <= (c -
��(c^2 - 4(a - b)d)/2(a - b)�C(c + ��(c^2 - 4(a - b)d)/2(a - b) <= x
����́C��̓��C�������C�̗����̓ʂ��O���̗̈�C�Ɖ��߂ł��܂��B
�Ȃ��C��̓����ڂ���ꍇ�ɂ́Cx �͂��ׂĂ̒l�����܂��B
(2-2) a < b �̏ꍇ
(a - b)x^2 - cx
- d <= 0
���̎��̍��ӂ́Cax^2
- (bx^2 + cx + d) �ƕό`�ł��C
= 0 �Ƃ������Ƃ��� x �́C��̓��̋��L�_�� x ���W�ɂȂ��Ă��܂��B
�܂��Cx^2 �̌W�� a - b < 0 �ɒ��ӂ��܂��B
(2-2-1) c^2
< 4(a - b)d �̏ꍇ�C��̓������L�_�������Ȃ��ꍇ
x �́C���ׂĂ̒l�����܂��B
(2-2-2) c^2
>= 4(a - b)d �̏ꍇ�C��̓������L�_�����ꍇ
x <= (c -
��(c^2 - 4(a - b)d)/2(a - b)�C(c + ��(c^2 - 4(a - b)d)/2(a - b) <= x
������C��̓��C�������C�����̓ʂ��O���̗̈�C�Ɖ��߂ł��܂��B
�Ȃ��C��̓����ڂ���ꍇ�ɂ́Cx �͂��ׂĂ̒l�����܂��B
�ȏ�ł��ׂĂł��B
�����̂��Ƃ̂����C�}�`�I�ɉ��߂������͍̂��W���̕��s�ړ�fr���ς��܂���B
�����ŁC�܂Ƃ߂�ƁC
R(x,y) �̋O�Ղ́C��̓�����̍��������������ŕ\����钼���ŁC
��̓��C�������C�����̓ʂ��O���̗̈�̕����C�Ƃ������ƂɂȂ�܂��B
�܂�C���̒����̂����C
�E��̓������L�_�����ꍇ�C
�E�E��_����̂Ƃ��C���̊Ԃ�����������
�E�E�ڂ���Ƃ��C���ׂĂ̗̈�̕���
�E�E��̓��̓̍��̌W������������_�������Ƃ��C
�E�E�E�̍�
> 0 �Ȃ�C��_��艺�̕���
�E�E�E�̍�
< 0 �Ȃ�C��_����̕���
�E��̓������L�_�������Ȃ��ꍇ�C���ׂĂ̗̈�̕���
�ƂȂ�悤�ł��B
��_�������ꍇ�ɂ́C���1�F�Ō����悤�ɁC
��̓�����̍��������������́C���̓�̌�_��ʂ钼���Ȃ̂ŁC
��_���������̂�����̕������̊O���C�Ƃ������܂��ˁB
(���z)
����́C�ǂ���������[�����ł����B
���ɁC���2�F�ŁC��̓��Ɍ�_�������ꍇ�ɁC
��̓�����̍������������������̓�̌�_��ʂ钼���ɂȂ邱�Ƃ͒m���Ă��܂������C
�ڐ��̌�_�̋O�Ղɂ����ꂪ�����̂͒m��܂���ł����B
���ɂȂ�܂����B
�m�n�Q�uMVH�v
06/10 12��39����M �X�V6/12
 �@
�@
�F����A�������킩������A�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA
���[���ő����Ă��������B�҂��Ă��܂��B
