平成23年12月4日
 [流れ星]
[流れ星]
第266回数学的な応募問題解答
<解答募集期間:11月13日〜12月4日
[モローの不等式]
日本実業出版社の「数検の完全対策1〜3級」からモローの不等式を変形して出題しました。

追記:「モローがどんな数学者か」 私には分かっていません。
<お詫び:eは自然対数の底数です。11月27日訂正>
NO1「uchinyan」 11/13 15時46分受信
「uchinyan」 11/13 17時56分受信
更新12/4
第266回数学的な応募問題
[モローの不等式]
2n/(2n+1)
< 1/e * (1 + 1/n)^n < (2n+1)/(2n+2),n は整数
まず,n > 0 の場合を考えます。
さらに,n を正の実数 x に置き換えて,
2x/(2x+1)
< 1/e * (1 + 1/x)^x < (2x+1)/(2x+2),x > 0
を証明します。n は正の実数の一部なので,これがいえれば元の不等式で n > 0 の場合もいえます。
ここで,両辺の自然対数を取ります。
log(2x/(2x+1))
< log(1/e * (1 + 1/x)^x) < log((2x+1)/(2x+2))
log(2x)
- log(2x+1) < x * log(x+1) - x * log(x) - 1 < log(2x+1) - log(2x+2)
log
は単調増加関数なので逆もいえ,この自然対数を取った式が証明できればいいです。
f(x)
= x * log(x+1) - x * log(x) - 1 - log(2x) + log(2x+1)
g(x)
= log(2x+1) - log(2x+2) - x * log(x+1) + x * log(x) + 1
と置きます。x > 0 で f(x) > 0,g(x) > 0 がいえればいいことになります。微分すると,
f'(x)
= log(x+1) - log(x) - 1/(x+1) - 1/x + 2/(2x+1)
g'(x)
= 2/(2x+1) - log(x+1) + log(x)
f''(x)
= 1/(x+1) - 1/x + 1/(x+1)^2 + 1/x^2 - 4/(2x+1)^2
=
((x^2 + x + 1)(4x^2 + 4x + 1) - 4(x^4 + 2x^3 + x^2))/(x(x+1)(2x+1))^2
=
(5x^2 + 5x + 1)/(x(x+1)(2x+1))^2
g''(x)
= - 4/(2x+1)^2 - 1/(x+1) + 1/x
=
((4x^2 + 4x + 1) - 4(x^2 + x))/x(x+1)(2x+1)^2
=
1/x(x+1)(2x+1)^2
x
> 0 なので,f''(x) > 0,g''(x) > 0 となって,f'(x),g'(x) は単調増加で,
f'(x)
< lim[x->+∞]{f'(x)} = lim[x->+∞]{log(1
+ 1/x) - 1/(x+1) - 1/x + 2/(2x+1)} = 0
g'(x)
< lim[x->+∞]{g'(x)} = lim[x->+∞]{2/(2x+1)
- log(1 + 1/x)} = 0
そこで,f(x),g(x) は単調減少で,lim[x->+∞]{(1 + 1/x)^x} = e なので,
f(x)
> lim[x->+∞]{f(x)} = lim[x->+∞]{log((1
+ 1/x)^x) - 1 + log(1 + 1/2x)} = 0
g(x)
> lim[x->+∞]{g(x)} = lim[x->+∞]{-
log(1 + 1/(2x+1)) - log((1 + 1/x)^x) + 1} = 0
つまり,x > 0 で,
f(x)
= x * log(x+1) - x * log(x) - 1 - log(2x) + log(2x+1) > 0
g(x)
= log(2x+1) - log(2x+2) - x * log(x+1) + x * log(x) + 1 > 0
となって,n > 0 では与えられた不等式は確かに成立します。
次に,n < 0 の場合です。これは,n -> -n,n > 0 と置き換えると,
2n/(2n-1)
< 1/e * (1 - 1/n)^(-n) < (2n-1)/(2n-2)
2n/(2n-1)
< 1/e * (1 + 1/(n-1))^(n-1) * n/(n-1) < (2n-1)/(2n-2)
ここで,n >= 2 ならば,n/(n-1) > 0 なので,
2n/(2n-1)
* (n-1)/n < 1/e * (1 + 1/(n-1))^(n-1) < (2n-1)/(2n-2) * (n-1)/n
2(n-1)/(2(n-1)+1)
< 1/e * (1 + 1/(n-1))^(n-1) < (2(n-1)+1)/(2(n-1)+2)
を証明すればいいですが,n-1 -> n と再度置き換えれば n > 0 の場合に帰着し,証明済みです。
n =
1,元の n =
-1 の場合は,1/0 が現れ,極限としても定義できないので,無意味です。
最後に,n = 0 の場合です。これは 1/n が存在しませんが,極限は考えることができます。
n
-> +0 の場合は,x = 1/n とおくと,
lim[n->+0]{(1 + 1/n)^n} = lim[x->+∞]{(1+x)^(1/x)}
= lim[x->+∞]{e^(log((1+x)^(1/x)))} = e^(lim[x->+∞]{log(1+x)/x})
ここで,x -> +∞ の状況を調べるために,x > 0 で f(x) = √x - log(1+x) を調べると,
f'(x)
= 1/(2√x) - 1/(1+x) = (√x - 1)^2/(2(1+x)√x)
で,x > 0 では f'(x) >= 0 で単調増加なので,
f(x)
> f(0) = √0 - log(1) = 0
となって,x > 0 で,
0
< log(1+x) < √x,0 < log(1+x)/x < 1/√x
lim[x->+∞]{log(1+x)/x} = 0
そこで,
lim[n->+0]{(1 + 1/n)^n} = e^0 = 1
になります。
n
-> -0 の場合は,x = -1/n とおくと,
lim[n->-0]{(1 + 1/n)^n} = lim[x->+∞]{(1-x)^(-1/x)}
= (lim[x->+∞]{(-1)^(1/x)})/(lim[x->+∞]{(x-1)^(1/x)})
= (lim[x->+∞]{(e^(i(2k+1)π))^(1/x)})/(lim[x->+∞]{e^(log((x-1)^(1/x)))})
=
(e^(lim[x->+∞]{i(2k+1)π/x})/(e^(lim[x->+∞]{log(x-1)/x}))
=
(e^(lim[x->+∞]{i(2k+1)π/x})/(e^(lim[x->+∞]{log(1 + (x-2))/(x-2) * (x-2)/x}))
=
((-1)^0)/(e^0) = 1
結局,lim[n->0]{(1 +
1/n)^n} = 1,になります。
そこで,不等式は,
0
< 1/e < 1/2
ですが,2 < e < 3 なので明らかに成立します。
以上より,
2n/(2n+1)
< 1/e * (1 + 1/n)^n < (2n+1)/(2n+2),n は -1 以外の整数
がいえました。
n =
-1 のときは,そもそも値が確定しないので,不等式が意味をもたないと思います。
(考察&感想)
n をいろいろと変えると,
(1
+ 1/n)^n * (2n+2)/(2n+1) < e < (1 + 1/n)^n * (2n+1)/2n
で e の近似値が求まりますが,両端の値は,例えば,
n =
1, 8/3, 3
n =
2, 27/10, 45/16
n =
3, 512/189, 224/81
n =
4, 3125/1152, 5625/2048
n =
5, 93312/34375, 42768/15625
n =
6, 823543/303264, 1529437/559872
n =
7, 33554432/12353145, 15728640/5764801
n =
8, 387420489/142606336, 731794257/268435456
n =
9, 20000000000/7360989291, 9500000000/3486784401
n =
10, 285311670611/105000000000, 544685916621/200000000000
...
となって,与えられている,19/7,193/71,2721/1001
は出て来ないようです。
これらの値はどうやって求めたのでしょうか?
それと,n = 0 の場合,特に n -> -0,は少し微妙です。n = -1 はナンセンスです。
まぁ,どうせ近似値には役には立たないし,あまり意味はなさそうなので,
n は自然数に限ってよさそうですね。
なお,モローという方は私も存じ上げないです。
<水の流れ:eの近似値は下記のものがあります。
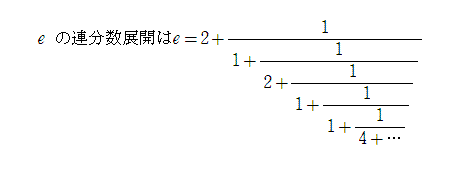
皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、
メールで送ってください。待っています。
