平成２４年１月１５日

[流れ星]

　　　　　第２６８回数学的な応募問題解答

　　　　　　＜解答募集期間：12月25日〜1月15日

［四面体の内接球］

問題１：　一辺の長さがaの正四面体OABCにおいて

（１）正四面体の体積 V をaを用いて表せ。

（２）正四面体に内接する球の半径 ｒ をaを用いて表せ。

（３）正四面体に外接する球の半径 R をaを用いて表せ。

（４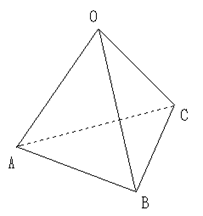）△OABに内接する円の平面ABCへの正射影の面積を求めよ。

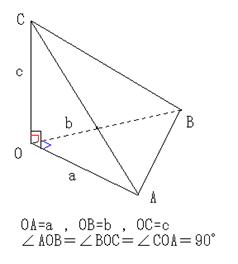
問題２：OA＝a , OB＝b , OC＝c で∠AOB＝∠BOC＝＝COA=90°

　　　さらに、ｂ＝ａ＋ｃとなる四面体OABCにおいて

（１）四面体に内接する球の半径 ｒ をa、ｃ　を用いて表せ。

（２）四面体に外接する球の半径 R をa、ｃ　を用いて表せ。

ＮＯ１「uchinyan」 12/25 15時12分受信

「uchinyan」 12/26 12時57分受信 更新1/15

問題１：(1)

一辺 a の正四面体は，一辺 a/√2 の立方体の対角線を一辺とする四面体になっています。

そこで，V は，立方体の体積から四つの頂点の回りの三角すいを引けばいいので，

V = (a/√2)^3 - (a/√2)^3 * 1/6 * 4 = √2/12 * a^3

(2)

内接球の中心を I とすると，I から各面に下ろした垂線の長さが r です。

そこで，△ABC = √3/4 * a^2 に注意して，

正四面体OABC = 三角すいI-OAB + 三角すいI-OBC + 三角すいI-OCA + 三角すいI-ABC

V = 三角すいI-ABC * 4 = △ABC * r * 1/3 * 4

√2/12 * a^3 = √3/4 * a^2 * r * 4/3

r = √6/12 * a

(3)

正四面体は，(1)の立方体に内接しているので，

正四面体の外接球と立方体の外接球は一致します。そこで，

R = √((a/√2)^2 + (a/√2)^2 + (a/√2)^2)/2 = √6/4 * a

(4)

まず，△OAB の内接円の半径は √3/2 * a * 1/3 = √3/6 * a で，面積は π/12 * a^2 です。

これを △ABC に正射影すると，AB 方向の長さは変わりませんが，

AB に垂直な方向は (√3/6 * a)/(√3/2 * a) = 1/3 倍になります。

そこで，面積は π/12 * a^2 * 1 * 1/3 = π/36 * a^2 になります。

正射影は，要するに楕円ですね。

(別解)

次のように解いてもいいでしょう。

(1)

O から △ABC に垂線を下ろしその足を G とします。

対称性より，G は △ABC の重心になります。そこで，AG の延長と BC の交点を H とすれば，

AH = √3/2 * a，AG = √3/3 * a，OG = √(OA^2 - AG^2) = √6/3 * a

また，△ABC = √3/4 * a^2 なので，

V = △ABC * OG * 1/3 = √3/4 * a^2 * √6/3 * a * 1/3 = √2/12 * a^3

(2)及び(3)

(1)における △OAH は △ABC だけでなく △OBC とも垂直です。

そこで，A から △OBC に垂線を下ろしその足を G' とすれば，

対称性より，G' は △OBC の重心で，G' は OH 上にあります。

OG と AG' との交点を I とします。すると，メネラウスの定理より，

OI/IG * GA/AH * HG'/G'O = 1，OI/IG * 2/3 * 1/2 = 1，OI/IG = 3/1

つまり，I は OG を 3：1 に内分する点です。同様にして，AI：IG' = 3：1 もいえます。

同様に B，C からも対面に垂線を下ろして同様の議論をすると，

これらの垂線は，すべて，OG を 3：1 に内分する点，つまり I，で交わることが分かります。

そこで，I は，内接球，外接球の中心になり，

r = IG = OG * 1/4 = √6/3 * a * 1/4 = √6/12 * a

R = IO = OG * 3/4 = √6/3 * a * 3/4 = √6/4 * a

(4)

これは，先ほどと同じです。

ただ，この解法の方が 1/3 倍をイメージしやすいかも知れません。

問題２：

(1)

まず，正四面体OABC の体積 V は，

正四面体OABC = V = abc/6 = ac(a + c)/6

そして，内接球の中心を I とすると，I から各面に下ろした垂線の長さが r で，

正四面体OABC = 三角すいI-OAB + 三角すいI-OBC + 三角すいI-OCA + 三角すいI-ABC

V = △OAB * r * 1/3 + △OBC * r * 1/3 + △OCA * r * 1/3 + △ABC * r * 1/3

r = 3V/(△OAB + △OBC + △OCA + △ABC)

ここで，b = a + c なので，△ABC は一辺 b = a + c の正方形に埋め込むことができ，

そのときの余分な部分が，△OAB，△OBC，△OCA とそれぞれ合同になるので，

△OAB + △OBC + △OCA + △ABC = b^2 = (a + c)^2

これより，

r = 3V/(△OAB + △OBC + △OCA + △ABC) = 3(ac(a + c)/6)/((a + c)^2)

r = 1/2 * ac/(a + c)

(2)

この四面体の外接球は，辺の長さが a，b，c の直方体の外接球と一致するので，

R = √(a^2 + b^2 + c^2)/2

b = a + c なので，

R = √(a^2 + (a + c)^2 + c^2)/2 = √((a^2 + ac + c^2)/2)

(別解)

次のように解いてもいいでしょう。

(1)

O(0,0,0)，A(a,0,0)，B(0,b,0)，C(0,0,c)，と座標を入れます。

すると，内接球の中心は，半径を r として，(r,r,r) で，

しかも，△ABC，x/a + y/b + z/c = 1，との距離も r です。

|r/a + r/b + r/c - 1|/√((1/a)^2 + (1/b)^2 + (1/c)^2) = r

(r,r,r) は O(0,0,0) の側にあることに注意して絶対値をはずして，

(1 - (r/a + r/b + r/c))/√((1/a)^2 + (1/b)^2 + (1/c)^2) = r

r = 1/((1/a + 1/b + 1/c) + √((1/a)^2 + (1/b)^2 + (1/c)^2))

r = abc/((ab + bc + ca) + √((ab)^2 + (bc)^2 + (ca)^2))

b = a + c なので，

r = ac(a + c)/((a^2 + 3ac + c^2) + √(a^4 + 2a^3c + 3a^2c^2 + 2ac^3 + c^4))

= ac(a + c)/((a^2 + 3ac + c^2) + √((a^2 + c^2)^2 + 2ac(a^2 + c^2) + (ac)^2))

= ac(a + c)/((a^2 + 3ac + c^2) + √((a^2 + ac + c^2)^2))

= ac(a + c)/((a^2 + 3ac + c^2) + (a^2 + ac + c^2))

= ac(a + c)/(2(a^2 + 2ac + c^2))

= ac(a + c)/(2(a + c)^2)

r = 1/2 * ac/(a + c)

(2)

外接球の中心を P(x,y,z) とすると，

PA = PO，(x - a)^2 + y^2 + z^2 = x^2 + y^2 + z^2，x = a/2

PB = PO，x^2 + (y - b)^2 + z^2 = x^2 + y^2 + z^2，y = b/2

PC = PO，x^2 + y^2 + (z - c)^2 = x^2 + y^2 + z^2，z = c/2

つまり，P(a/2,b/2,c/2) です。そこで，

R = √((a/2)^2 + (b/2)^2 + (c/2)^2) = √(a^2 + b^2 + c^2)/2

b = a + c なので，

R = √(a^2 + (a + c)^2 + c^2)/2 = √((a^2 + ac + c^2)/2)

(考察)及び(感想)

問題２：の(1)は b = a + c が効いていますね。その(別解)はその関係に頼らない解法です。

一般の四面体の場合は，四面体をどう与えるかにもよりますが，面倒になりそうです。

ベクトルで与えた場合は，大学レベルの知識になりますが，ベクトル積＝外積も使えば，そこそこの計算で表現はできそうです。

ただ，それを，辺の長さや座標で書こうと思うと，大変なことになりそうです。

したがって？，ここでは省略します。

ＮＯ２「浜田明巳」 01/05 10時24分受信 更新1/15

問題１
　座標系を導入し，
　　Ａ(ａ／２，√３ａ／２，０)，Ｂ(０，０，０)，Ｃ(ａ，０，０)，Ｏのｚ座標は正，
　　内接球の中心をＯ'，Ｏから平面ＡＢＣに下ろした垂線の足をＨ，
　　ＢＣの中点をＩ
とする．

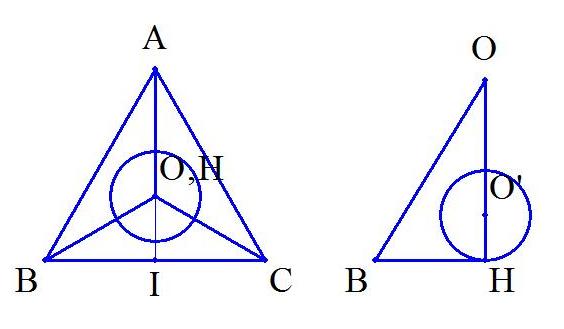
（１）△ＨＢＩにおいて，
　　∠ＨＢＩ＝∠ＡＢＣ／２＝３０°，∠ＨＩＢ＝９０°
　　∴ＨＩ＝ＢＩ／√３＝ａ／(２√３)，ＨＢ＝２ＨＩ＝ａ／√３
　△ＯＢＨにおいて，
　　ＯＨ^２＝ＯＢ^２−ＨＢ^２＝ａ^２−ａ^２／３＝２ａ^２／３
　　∴ＯＨ＝√２ａ／√３
　　∴Ｏ(ａ／２，ａ／(２√３)，√２ａ／√３)，Ｏ'(ａ／２，ａ／(２√３)，ｒ)
　　∴Ｖ＝１／３・△ＡＢＣ・ＯＨ＝１／３・√３ａ^２／４・√２ａ／√３＝√２ａ^３／１２

（２）平面ＯＢＣの方程式を，点Ｂ(０，０，０)を通ることから，
　　ｂｘ＋ｃｙ＋ｄｚ＝０………(1)
とする．
　点Ｃ(ａ，０，０)を通るので，ａｂ＝０
　ａ＞０なので，ｂ＝０
　点Ｏ(ａ／２，ａ／(２√３)，√２ａ／√３)を通るので，
　　ａｃ／(２√３)＋√２ａｄ／√３＝０
　ａ＞０なので，ｃ＋２√２ｄ＝０
　　∴ｃ＝−２√２ｄ
　(1)に代入すると，−２√２ｄｙ＋ｄｚ＝０
　ｂ＝０，ｃ＝−２√２ｄから，ｄ≠０
　　∴２√２ｙ−ｚ＝０
　点Ｏ'(ａ／２，ａ／(２√３)，ｒ)から，この平面までの距離は球の半径ｒなので，
　　ｒ＝｜２√２・ａ／(２√３)−ｒ｜／√{０^２＋(２√２)^２＋(−１)^２}
　　∴３ｒ＝｜√２ａ／√３−ｒ｜
　　∴９ｒ^２＝(√２ａ／√３)^２−２(√２ａ／√３)ｒ＋ｒ^２
　　∴(√２ａ／√３)^２−２(√２ａ／√３)ｒ−８ｒ^２＝０
　　∴(√２ａ／√３＋２ｒ)(√２ａ／√３−４ｒ)＝０
　ａ＞０，ｒ＞０から，ｒ＝ａ／(２√６)＝√６ａ／１２
（参考）他の解ｒ＝−ａ／√６は，その絶対値が，中心がｘｙ平面と点Ａの反対側にあり，平面ＯＡＢ，ＯＢＣ，ＯＣＡに接する球の半径を表している．

（３）対称性から，外接球の中心は，内接球の中心Ｏ'(ａ／２，ａ／(２√３)，ａ／(２√６))と一致する．
　　∴Ｒ＝Ｏ'Ｂ＝ａ／２・√{１^２＋(１／√３)^２＋(１／√６)^２}＝ａ／２・√(１＋１／３＋１／６)＝ａ／２・３／√６＝√３ａ／(２√２)＝√６ａ／４


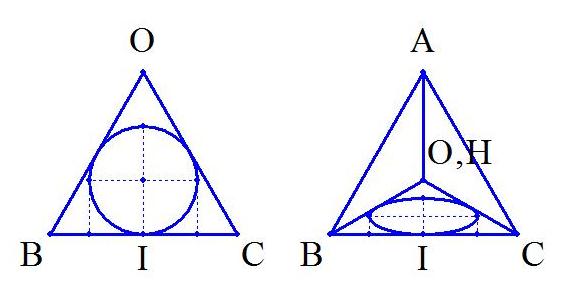
（４）対称性から，△ＯＢＣの内接円の平面ＡＢＣへの正射影の面積を求めればよい．
　△ＯＢＣの内接円の半径をｒ'とすると，この正三角形の面積は，
　　√３ａ^２／４＝(ａ＋ａ＋ａ)／２・ｒ'
　ａ＞０から，ｒ'＝ａ／(２√３)
　求める面積Ｓは，図の△ＨＢＣに内接する楕円の面積となる．
　長径の長さは，
　　２・ｒ'＝２・ａ／(２√３)
　短径の長さは，
　　２・ｒ'・(Ｈのｙ座標)／(Ａのｙ座標)＝２・ａ／(２√３)・ａ／(２√３)／(√３ａ／２)＝２・ａ／(２・３√３)＝２・ａ／(６√３)
　　∴Ｓ＝π・ａ／(２√３)・ａ／(６√３)＝πａ^２／３６

問題２
（１）Ｏ(０，０，０)，Ａ(０，−ａ，０)，Ｂ(ａ＋ｃ，０，０)，Ｃ(０，０，ｃ)，
　内接球の中心をＯ'(ｒ，−ｒ，ｒ)
とする．

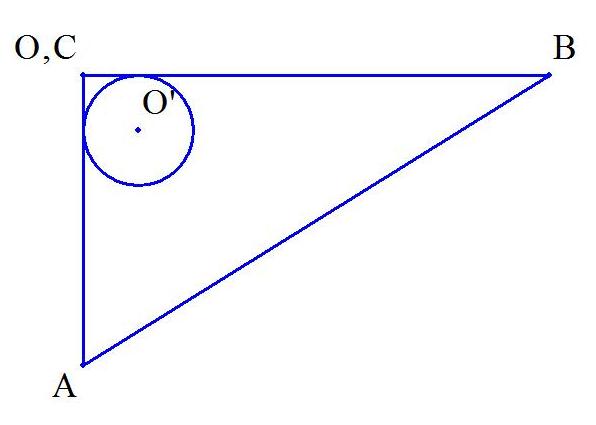
　平面ＡＢＣの方程式を，点Ａを通ることより，
　　ｋｘ＋ｍ(ｙ＋ａ)＋ｎｚ＝０………(1)
とする．
　点Ｂ，Ｃを通るので，
　　ｋ(ａ＋ｃ)＋ａｍ＝０，ａｍ＋ｃｎ＝０
　ａ＋ｃ＞０，ｃ＞０であるから，ｋ＝−ａｍ／(ａ＋ｃ)，ｎ＝−ａｍ／ｃ
　(1)に代入すると，
　　−ａｍ／(ａ＋ｃ)・ｘ＋ｍ(ｙ＋ａ)−ａｍ／ｃ・ｚ＝０
　ｍ≠０から，
　　−ａｃｘ＋ｃ(ａ＋ｃ)ｙ−ａ(ａ＋ｃ)ｚ＋ａｃ(ａ＋ｃ)＝０
　球の中心Ｏ'(ｒ、−ｒ、ｒ)からこの平面までの距離は，球の半径ｒに等しいので，
　　ｒ＝｜−ａｃｒ−ｃ(ａ＋ｃ)ｒ−ａ(ａ＋ｃ)ｒ＋ａｃ(ａ＋ｃ)｜／√{ａ^２ｃ^２＋ｃ^２(ａ＋ｃ)^２＋ａ^２(ａ＋ｃ)^２}
　　∴{ａ^２ｃ^２＋(ａ^２＋ｃ^２)(ａ＋ｃ)^２}ｒ^２＝[ａｃ(ａ＋ｃ)−{(ａ＋ｃ)^２＋ａｃ}ｒ]^２
　　∴{(ａ^２＋ｃ^２)^２＋ａ^２ｃ^２＋２ａｃ(ａ^２＋ｃ^２)}ｒ^２＝ａ^２ｃ^２(ａ＋ｃ)^２−２ａｃ(ａ＋ｃ)(ａ^２＋３ａｃ＋ｃ^２)ｒ＋(ａ^２＋３ａｃ＋ｃ^２)^２ｒ^２
　　∴(４ａ^３ｃ＋８ａ^２ｃ^２＋４ａｃ^３)ｒ^２−２ａｃ(ａ＋ｃ)(ａ^２＋３ａｃ＋ｃ^２)ｒ＋ａ^２ｃ^２(ａ＋ｃ)^２＝０
　ａｃ＞０から，
　　(ａ＋ｃ)^２(２ｒ)^２−(ａ＋ｃ)(ａ^２＋３ａｃ＋ｃ^２)・２ｒ＋ａｃ(ａ＋ｃ)^２＝０
　ａ＋ｃ＞０から，
　　(ａ＋ｃ)(２ｒ)^２−(ａ^２＋３ａｃ＋ｃ^２)・２ｒ＋ａｃ(ａ＋ｃ)＝０
　　∴{２ｒ−(ａ＋ｃ)}{(ａ＋ｃ)・２ｒ−ａｃ}＝０
　ａ＋ｃ＞０から，
　　ｒ＝(ａ＋ｃ)／２，ａｃ／{２(ａ＋ｃ)}
　図のｘｙ平面において，点Ｏ'をｘｙ平面に投影した点は，直線ＡＢの上側にあるので，
　　０＜ｒ＜ａ，０＜ｒ＜ａ＋ｃ，−ｒ＞{０−(−ａ)}／{(ａ＋ｃ)−０}・(ｒ−０)−ａ＝ａｒ／(ａ＋ｃ)−ａ
　　∴０＜ｒ＜ａ，０＜ｒ＜ａ(ａ＋ｃ)／(２ａ＋ｃ)
　任意のａ，ｃについて成立するので，ｒ＝ａｃ／{２(ａ＋ｃ)}
（参考）ｒ＝(ａ＋ｃ)／２は，平面ＡＢＣに外側で接している球の半径である．

（２）外接球の中心をＯ''(ｘ，ｙ，ｚ)とする．
　この球とｘｙ平面との交線の円の中心をＯ'''(ｘ，ｙ，０)とすると，この円の半径は，
　　Ｏ'''Ｏ＝Ｏ'''Ａ＝Ｏ'''Ｂ
　　∴ｘ^２＋ｙ^２＝ｘ^２＋(ｙ＋ａ)^２＝{ｘ−(ａ＋ｃ)}^２＋ｙ^２
　　∴０＝２ａｙ＋ａ^２＝−２(ａ＋ｃ)ｘ＋(ａ＋ｃ)^２
　ａ＞０，ａ＋ｃ＞０から，
　　ｘ＝(ａ＋ｃ)／２，ｙ＝−ａ／２
　　∴Ｏ''((ａ＋ｃ)／２，−ａ／２，ｚ)
　また，Ｒ＝Ｏ''Ａ＝Ｏ''Ｃ
　　∴{(ａ＋ｃ)／２}^２＋{−ａ／２−(−ａ)}^２＋ｚ^２＝{(ａ＋ｃ)／２}^２＋(−ａ／２)^２＋(ｚ−ｃ)^２
　　∴０＝−２ｃｚ＋ｃ^２
　ｃ＞０から，ｚ＝ｃ／２
　　∴Ｏ''((ａ＋ｃ)／２，−ａ／２，ｃ／２)
　　∴Ｒ＝Ｏ''Ｃ＝√[{(ａ＋ｃ)／２}^２＋(−ａ／２)^２＋(ｃ／２−ｃ)^２]＝√{２(ａ^２＋ａｃ＋ｃ^２)}／２

＜水の流れコメント：問題１の（４）は△OABに内接する円の面積Ｓと平面ABCへの正射影の面積Ｔの間にはＴ＝Ｓｃｏｓθ（θは平面OABと平面ABCのなす角）があります。

問題２は求める内接球の半径をｒとしたとき、四面体OABCの表面積Ｓと体積Ｖとの間にＶ＝（1／3）ｒＳの関係があります。さらに、四面体OABCの表面積Ｓは１辺がｂの正方形の中に覆われることができます。実は、この妙技を分かってもらうためにｂ＝a＋ｃとしたのです。また、外接球の直径は３辺の長さがａ，ｂ，ｃでできる直方体の対角線の長さになります。四面体の体積を求めるのに外積を利用して教えたこともあります。＞

皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。