�����Q�U�N�S���P�R��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��304�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF�R��16���`�S��13����
�m�告�o�̐���\�n
�������ܑ告�o�t�ꏊ�����{���̈�قōs���Ă��܂��B����͎m�̏��ꏊ�̏��s�́�������������������������������8��7�s�ł����B������Q���Ԃŕ��͂����Ƃ��끛�����R��A�������T��A�������S��A�������Q��ɂȂ�܂��B
���P�F�Q���Ԃ̕��͌��ʂ���Ɠ����������R��A�������T��A�������S��A�������Q��ƂȂ�悤�Ȑ���\�͑S���ʼn��ʂ肠�邩�B
���Q�F�Q���Ԃ̕��͌��ʂׂ��灜����������B���̂悤�Ȑ���\�͂P�T���Ԃōl�����Ƃ��S���ʼn��ʂ肠�邩�B
NO1�uuchinyan�v 03/16 13��18���@��M
���P�F
������ 5 ��ƁC�����̊Ԃɂ͕K�������� 1 ���v 4 ��܂��B
�����ŁC������ 5 ���ׂĂ����āC���̑O�Ɂ������v�� 3 �C���̌�Ɂ������v�@2 �C���ݍ��߂����ł��B
���̕��́C
�������P�Ƃ� 3 ���ꍇ�C5C3 = 10 �ʂ�
������ 1 ��C�������� 1 ��C�����ꍇ�C5C2 * 2 = 20 �ʂ�
���������� 1 ���ꍇ�C5C1 = 5 �ʂ�
�ŁC���v 10 + 20 + 5 = 35 �ʂ�B
���̕��́C
�������P�Ƃ� 2 ���ꍇ�C5C2 = 10 �ʂ�
�������� 1 ���ꍇ�C5C1 = 5 �ʂ�
�ŁC���v 10 + 5 = 15 �ʂ�B
�����̌�����͓Ɨ��Ȃ̂ŁC�������|���āC
35 * 15 = 525 �ʂ�
�ɂȂ�܂��B
���Q�F
�v����ɁC�����A�����Č���Ȃ�������ł��B
���� 0 ��̏ꍇ
1 �ʂ�B
���� 1 ��̏ꍇ
15 �ʂ�B
���� 2 ��̏ꍇ
���Ɓ��̊ԂɁ������Ȃ��Ƃ� 1 �������̂ŁC���Ɓ��̊ԂɁ����ŏ��� 1 �u���āC�c��́��Ŗ��߂āC
3H(15-2-1) = 3H12 = 14C12 = 91 �ʂ�B
���� 3 ��̏ꍇ
���l�ɍl���āC4H(15-3-2) = 4H10 =
13C10 = 286 �ʂ�B
���� 4 ��̏ꍇ
���l�ɍl���āC5H(15-4-3) = 5H8 =
12C8 = 495 �ʂ�B
���� 5 ��̏ꍇ
���l�ɍl���āC6H(15-5-4) = 6H6 =
11C6 = 462 �ʂ�B
���� 6 ��̏ꍇ
���l�ɍl���āC7H(15-6-5) = 7H4 =
10C4 = 210 �ʂ�B
���� 7 ��̏ꍇ
���l�ɍl���āC8H(15-7-6) = 8H2 =
9C2 = 36 �ʂ�B
���� 8 ��̏ꍇ
���l�ɍl���āC9H(15-8-7) = 9H0 =
8C0 = 1 �ʂ�B
���� 9 ��ȏ�̏ꍇ
���炩�� 0 �ʂ�B
�ȏ�ł��ׂĂȂ̂ŁC
1 + 15 + 91 + 286 + 495 + 462 + 210 + 36 + 1
= 1597 �ʂ�
�ɂȂ�܂��B
(�ʉ�)
n ����������Ɂ�������x���Ȃ��Cn ��ڂ̎������C���̏ꍇ�� a(n) �ʂ�C���̏ꍇ�� b(n) �ʂ�C�Ƃ���ƁC
a(n+1) = a(n) + b(n)�Cb(n+1) = a(n)�Ca(1) = 1�Cb(1) = 1
�Ə����܂��B�����ŁC
a(n) = a(n-1) + a(n-2)�Cb(n) = a(n-1)�Ca(1) = 1�Ca(2) = 2
������Ca(n) �́Ca(0) = 1 �Ƃ����ꍇ�̃t�B�{�i�b�`����ŁC
���߂�̂� a(15) + b(15) = a(15)
+ a(14) = a(16) �Ȃ̂ŁC
a(3) = 3�Ca(4) = 5�Ca(5) = 8�Ca(6) = 13�Ca(7)
= 21�Ca(8) = 34�Ca(9) = 55�Ca(10) = 89�C
a(11) = 144�Ca(12) = 233�Ca(13) = 377�Ca(14) = 610�Ca(15) = 987�Ca(16) = 1597
�����ŁC1597 �ʂ�C�ɂȂ�܂��B
(���z)
����͂悭����p�^�[���̖��ŁC���̃T�C�g�ł��ȑO�ɗޑ肪�������Ǝv���܂��B
���ɁC���Q�F���t�B�{�i�b�`����ɂȂ�̂͂悭�m��ꂽ���Ƃ̂悤�Ɏv���܂��B
�悢���K�ɂȂ�܂����B
NO2�u���N���̂�������v 03/18 16��11���@��M
���1
�u2���Ԃ̕��́v�ɂ��ƁA�����Ɛ�H�y�̏��s��1�����A2���ڂ���14���ڂ̏��s��2�����܂��B
�i���j������3��A������5��A������4��A������2��Ȃ̂ŁA
�����́A2�~3�{5�{4��15�A�����́A5�{4�{2�~2��13�ɂȂ�܂��B
�܂�A������15�^2��7.5�ȏ�i8.5�����j�A�����́A13�^2��6.5�ȏ�i7.5�����j�ƂȂ�̂ŁA�m����8��7�s�ł��B
�����Ɛ�H�y�̏��s���قȂ�ꍇ�́A���̏ꍇ�̗l�ɒ[�����o�܂��B
�����Ɛ�H�y�̏��s�������ꍇ�́A�[���͏o���A���̐���1���Ȃ��Ȃ�܂��B
�i�Ⴆ�Ώ����Ɛ�H�y�������Ȃ�A������1���Ȃ��Ȃ�܂��j
8��7�s�Łi���j�̂悤�Ȋ��U��ɂȂ�ꍇ���l���܂��B
�E�܂�������8�l���܂��B
�@�@�@���O���O���O���O���O���O���O��
�@���̏�Ԃ́�����7��ł��B
�E�i���j�́�����3��Ȃ̂ŁA7�̊ԁi�O�j�̈قȂ�4���Ɂ������܂��B�i��![]() �j
�j
�@�Ⴆ�A
�@�@�@������������������������
�@����ƁA������3��ɂȂ�A�����Ɓ����͂Ƃ���4��ɂȂ�܂��B
�E������5��ɂ��邽�߂ɁA�Ō�Ɂ���t�������܂��B
�@�@�@��������������������������
�E5�����́��̂����ǂ���2�����ɏd��������������t�������܂��B�i��![]() �j
�j
�@�Ⴆ�A
�@�@�@������������������������������
�@����ƁA�i���j������3��A������5��A������4��A������2��ƂȂ�܂��B
�䂦�ɁA���߂鐯��\��![]() �ʂ肠��܂��B
�ʂ肠��܂��B
���2
���������̂́A�������{1�̊ԁi�O�j�ł��B
�O���O���O���O���O�E�E�E�O���O���O���O
�u2���Ԃ̕��́v�Ł��������̏ꍇ�́A���̏ꍇ�ł��B
�E15��0�s�̂Ƃ��@![]()
�E14��1�s�̂Ƃ��@![]()
�E13��2�s�̂Ƃ��@![]()
�E12��3�s�̂Ƃ��@![]()
�E11��4�s�̂Ƃ��@![]()
�E10��5�s�̂Ƃ��@![]()
�E 9��6�s�̂Ƃ��@![]()
�E 8��7�s�̂Ƃ��@![]()
�E 7��8�s�̂Ƃ��@![]()
�ȏ㍇�v1597�ʂ�ł��B
�����łɁA8��7�s�̏ꍇ�̐���\�ɂ��āu2���Ԃ̕��́v�p�^�[���͈ȉ���27��ނł��B
���1��No17�ɂȂ�܂��B
|
No |
���� |
���� |
���� |
���� |
�ꍇ�̐� |
���l |
�@ |
|
1 |
7 |
1 |
1 |
5 |
6 |
�@ |
�@ |
|
2 |
7 |
1 |
0 |
6 |
1 |
�@8�A���̂���7�A�s |
|
|
3 |
7 |
0 |
1 |
6 |
1 |
�@7�A�s�̂���8�A�� |
|
|
4 |
6 |
2 |
2 |
4 |
105 |
�@ |
�@ |
|
5 |
6 |
2 |
1 |
5 |
42 |
�@ |
|
|
6 |
6 |
1 |
2 |
5 |
42 |
�@ |
|
|
7 |
6 |
1 |
1 |
6 |
7 |
�@ |
|
|
8 |
5 |
3 |
3 |
3 |
420 |
�@ |
�@ |
|
9 |
5 |
3 |
2 |
4 |
315 |
�@ |
|
|
10 |
5 |
2 |
3 |
4 |
315 |
�@ |
|
|
11 |
5 |
2 |
2 |
5 |
126 |
�@ |
|
|
12 |
4 |
4 |
4 |
2 |
525 |
�@ |
�@ |
|
13 |
4 |
4 |
3 |
3 |
700 |
�@ |
|
|
14 |
4 |
3 |
4 |
3 |
700 |
�@ |
|
|
15 |
4 |
3 |
3 |
4 |
525 |
�@ |
|
|
16 |
3 |
5 |
5 |
1 |
210 |
�@ |
�@ |
|
17 |
3 |
5 |
4 |
2 |
525 |
�@ |
|
|
18 |
3 |
4 |
5 |
2 |
525 |
�@ |
|
|
19 |
3 |
4 |
4 |
3 |
700 |
�@ |
|
|
20 |
2 |
6 |
6 |
0 |
21 |
�@ |
�@ |
|
21 |
2 |
6 |
5 |
1 |
126 |
�@ |
|
|
22 |
2 |
5 |
6 |
1 |
126 |
�@ |
|
|
23 |
2 |
5 |
5 |
2 |
315 |
�@ |
|
|
24 |
1 |
7 |
6 |
0 |
7 |
�@ |
�@ |
|
25 |
1 |
6 |
7 |
0 |
7 |
�@ |
|
|
26 |
1 |
6 |
6 |
1 |
42 |
�@ |
|
|
27 |
0 |
7 |
7 |
0 |
1 |
�@���݂ɏ������� |
�@ |
|
�@ |
���v |
6435 |
�@ |
||||
�W���V�s�̏��������̐���\�́A![]() �ʂ肠��܂��B
�ʂ肠��܂��B
���āA�g�����̋L���̍��̓Y����������������@![]() ���J��Ԃ��ėp����ƁA
���J��Ԃ��ėp����ƁA
![]()
�ƂȂ�܂��B
�����p���� ![]() ��ό`���Ă݂܂��B
��ό`���Ă݂܂��B
�܂��A���̓Y������7�����Ă݂܂��B
![]()
���ɁA![]() �ɒ��ӂ��āA���̓Y������8�̕�����1�����܂��B
�ɒ��ӂ��āA���̓Y������8�̕�����1�����܂��B
�܂��A���̓Y������7�̂��́i�W���j�͐��ɒ����Ă����܂��B
![]()
![]()
�����āA![]() ��p���ď��������ƁA
��p���ď��������ƁA
![]()
�ƂȂ�\�Ɠ����ɂȂ�܂��B
�p�X�J���̎O�p�`
|
|
||||||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
![]()
�����āA![]() ��p���ď��������ƁA
��p���ď��������ƁA
![]()
�ƂȂ�\�Ɠ����ɂȂ�܂��B
�p�X�J���̎O�p�`
|
|
||||||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
NO3�u���N���̂�������v 03/18 18��23���@��M
�����̗���R�����g�F�Q�A�s�������Ȃ�����\�͏����A����ځA�O���ڂƐ����Ă݂Ă��������B
�ʔ������ʂɂȂ�܂��B��
�ʔ������w�E���肪�Ƃ��������܂��B
1�����āA�t�B�{�i�b�`����ɂȂ�̂ł��ˁB
|
1 |
2 |
|
2 |
3 |
|
3 |
5 |
|
4 |
8 |
|
5 |
13 |
|
6 |
21 |
|
7 |
34 |
|
8 |
55 |
|
9 |
89 |
|
10 |
144 |
|
11 |
233 |
|
12 |
377 |
|
13 |
610 |
|
14 |
987 |
|
15 |
1597 |
���`�}�������Ƃ悭�킩��܂��B
���肪�Ƃ��������܂����B
NO4�u��x�Ђ����v 03/18 19��57�� ��M
|
���1:�@(5H2)*(5H3) = 15*35 = 525�ʂ�D(��) ������A�C������B�C������C�C������D �Ƃ��������ŕ\�����Ƃɂ��܂��D ���2:
��[k=0�`15]comb(k+1,15-k) =
1597 �ʂ�D(��) n���Ԃ̐���\�ɂ����āC������0��ƂȂ�悤�ȕ��@��a[n]�ʂ肠��Ƃ��܂��D ����āCa[n]=��[k=0�`n]comb(k+1,n-k)�D |
NO5�u�r�o�b�v3/28 15��35�� ��M
�p�\�R���������ł��B�ږ�̐搶�̎w���̂��ƁA�����Ă݂܂����B�p�\�R���̃Q�[���쐬�v���O�����g�r�o�ʼn����܂����B
�@�����O�A�����P�A���P����P�̓����A���Q����Q�̓����A���P�������̐��A���Q�������̐��A���R�������̐��A���S�������̐��Ƃ��܂��B
�i�v���O�����j
dim a,15
k1=0 : k2=0
repeat 2 : a(1)=cnt
repeat 2 : a(2)=cnt
repeat 2 : a(3)=cnt
repeat 2 : a(4)=cnt
repeat 2 : a(5)=cnt
repeat 2 :
a(6)=cnt
repeat
2 : a(7)=cnt
repeat 2 : a(8)=cnt
repeat 2 : a(9)=cnt
repeat 2 : a(10)=cnt
repeat 2 : a(11)=cnt
repeat 2 : a(12)=cnt
repeat 2 : a(13)=cnt
repeat 2 : a(14)=cnt
repeat 2 : a(15)=cnt
b1=0 : b2=0 : b3=0 : b4=0
repeat 14,1
if (a(cnt)=0)&(a(cnt+1)=0) : b1+
if (a(cnt)=0)&(a(cnt+1)=1) : b2+
if (a(cnt)=1)&(a(cnt+1)=0) : b3+
if (a(cnt)=1)&(a(cnt+1)=1) : b4+
loop
if (b1=3)&(b2=5)&(b3=4) : k1+
if b4=0 : k2+
loop
loop
loop
loop
loop
loop
loop
loop
loop
loop
loop
loop
loop
loop
loop
mes k1 : mes k2
�i�j
�T�Q�T
�P�T�X�V
NO6�u�ɂ���Z12�v4/06 22��40�� ��M
�ɂ���Z14�ł�
���P�F�Q���Ԃ̕��͌��ʂ���Ɠ����������R��A�������T��A�������S��A�������Q��ƂȂ�悤�Ȑ���\�͑S���ʼn��ʂ肠�邩
�������T��A�������S��Ƃ����̂�
���������������������E�E�E�@
�̌`�������������i�܂�����Ɂj�������𑫂���������܂���
�܂聜�ł����ł����ɓ��������
�������T��A�������S����Ȃ��킯�ł�
���̂��Ƈ@�͏����Ɛ�H�y���l����Ƃ킩��܂�
�����Ɛ�H�y�̃P�[�X�킯�����܂�
�E�E�E�ɉ������Ă��A�����铯���F��1�̂����ď�����
���E�E�E���������Ɓ����͓����@�@�@�@�@�@�i1�@�i�E�E�E�Ɂ������Ȃ��ꍇ�����Ƃ�0�j
���E�E�E���������Ɓ����́�����1�����@�i2
���E�E�E���������Ɓ����͓����@ �@�@�@�i3�@�i�E�E�E�Ɂ������Ȃ��ꍇ�����Ƃ�0�j
���E�E�E���������Ɓ����́�����1�����@�i4
�Ȃ̂Ň@�́i2�j�̌`���Ƃ肩�A���̒���
���������������������Ȃ��Ắ������T��A�������S��
����邱�Ƃ��ł��܂���B
�����Łi�Čf�j
���������������������E�E�E�@
����{�Ƃ�
������3��A
������2��B
���l�����
�@�Ɂ����́���1������Ɗe�X�����A������1���Ă����܂�
�܂�A���������͇@�́���3�������`�ł����A������3�J�E���g����܂�
�����A�A�B�͇@�̓����Ɂ���3����2�����ꍇ�̐������߂���ɋA������܂��B
����́Am�̃{�[����n�̔��ɓ����ꍇ�ɑ�������̂ŏd���g�ݍ��킹mHn�Ōv�Z�ł��܂�
�����
�A�̏ꍇ�̐���m=3,n=5�Ƃ�
mHn��m+n-1�bn-1��7�b4��35
�B�̏ꍇ�̐���m=2,n=5�Ƃ�
mHn��m+n-1�bn-1��6�b4��15
�ƂȂ�A�A�ƇB�͓Ɨ��Ȃ̂�
�ꍇ�̐���
35�~15��525�ʂ�ƂȂ�܂��E�E�E�E��
���Q�F�Q���Ԃ̕��͌��ʂׂ��灜����������B���̂悤�Ȑ���\�͂P�T���Ԃōl�����Ƃ��S���ʼn��ʂ肠�邩�B
���1�Ɠ��l�ɍl����Ə����i1�j�i2�j�i4�j�̃P�[�X�ɂ����ā��݂̂�����ꍇ�̐����v�Z����悢���Ƃ��킩��܂��B
�i1�j�i2�j�̃P�[�X
���E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����14�@�@14�b0
=1�@�@�i�S���D���̏ꍇ�j
�����E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����13�@
�@13�b0 =1
�������E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����12�@�@13�b1
=13
���������E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����11�@
�@12�b1 =12
�����������E�E�E�E�E�E�E�E�E�E�E�E�E�E����10�@�@12�b2
=66
�������������E�E�E�E�E�E�E�E�E�E�E�E�E����9�@
�@11�b2 =55
���������������E�E�E�E�E�E�E�E�E�E�E�E����8�@ �@11�b3
=165
�����������������E�E�E�E�E�E�E�E�E�E�E����7�@
�@10�b3 =14
�������������������E�E�E�E�E�E�E�E�E�E����6�@ �@10�b4
=120
���������������������E�E�E�E�E�E�E�E�E����5�@
�@9�b4 =210
�����������������������E�E�E�E�E�E�E�E����4�@ �@9�b5
=126
�������������������������E�E�E�E�E�E�E����3�@
�@8�b5 =56
���������������������������E�E�E�E�E�E����2�@ �@8�b6
=28
�����������������������������E�E�E�E�E����1�@
�@7�b6 =7
�������������������������������E�E�E�E����0�@ �@7�b7
=1
�i3�j�i4�j�̃P�[�X
�����E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����13�@
�@13�b0 =1
�������E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����12�@�@12�b0
=1
���������E�E�E�E�E�E�E�E�E�E�E�E�E�E�E����11�@
�@12�b1 =12
�����������E�E�E�E�E�E�E�E�E�E�E�E�E�E����10�@�@11�b1
=11
�������������E�E�E�E�E�E�E�E�E�E�E�E�E����9�@
�@11�b2 = 55
���������������E�E�E�E�E�E�E�E�E�E�E�E����8�@ �@10�b2
=45
�����������������E�E�E�E�E�E�E�E�E�E�E����7�@
�@10�b3 =120
�������������������E�E�E�E�E�E�E�E�E�E����6�@ �@9�b3
=84
���������������������E�E�E�E�E�E�E�E�E����5�@
�@9�b4 =126
�����������������������E�E�E�E�E�E�E�E����4�@ �@8�b4
=70
�������������������������E�E�E�E�E�E�E����3�@ �@ 8�b5 =56
���������������������������E�E�E�E�E�E����2�@ �@7�b5
=21
�����������������������������E�E�E�E�E����1�@
�@7�b6 =7
�������������������������������E�E�E�E����0�@ �@6�b6
=1
�����𑫂����킹��Ɓ@1,597�ʂ�ƂȂ�܂��B�E�E�E�E��
���2�Ɋւ��Ă͂����ƃG���K���g�ŁA���1�ƑS����������_�ʼn������@������̂��Ǝv���܂���
���Ԃ�����܂���ł����B�i�Ƃ������͐s�����Ƃ����̂��{���ł��傤���B�搶�̂����������g�A�z�h�ɂ͎���܂���ł����j
�������1�̉ɂ��ǂ蒅���܂ŁA���\��̎��s��������܂����̂ŁB�i���͂��ׂĂ𐔂��グ���̂����s����̈�Ńp�\�R�����g���Ȃ����1��������܂����j
�F����̃G���K���g�ȉ�@�݂�̂��y���݂ł��B
�u�ɂ���Z12�v�@4/10 23��05�� ��M �X�V 04/13
���Q�i�ʉ��j
���낢�뎎�������Ƃ͑O���܂������������{�̎��`�}���l���Ȃ������̂͒p������������ł��B
���͔�����������܂Ȃ��B���͍��Ɣ����P�����ށB
�����l����ƈ���ځ��Q���ځ��R���ځ����E�E�E�̂悤�Ɏ��`�}���`���܂��B
�@���̎�n���ڂ́��͂�-1���ڂ́��̌��Ɓ��̌��̘a�ɓ������An���ڂ́��͂�-1���ڂ́��̌��ɓ�����
�����}�ŕ\����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ 
�܂��A�\�ŕ\����
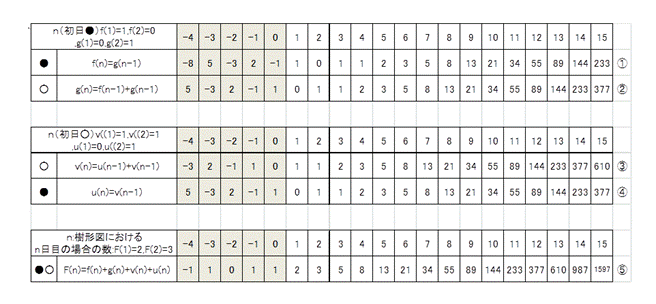
�����ŁAf(n)=g(n-1)�@����Af(n-1)=g(n-2�j�Ȃ̂�
g(n)=f(n-1)+g(n-1)=g(n-2�j+g(n-1)�E�E�E�E�A-1
�܂�g(n)=f(n-1)+g(n-1)�A����
g(n-1)=f(n-2)+g(n-2)
�ӁX�����Đ��������
f(n-1)+f(n-2)=g(n)-g(n-2)=g(n-1)=f(n)�F�����������
f(n)=f(n-1)+f(n-2)�E�E�E�@-1
���l�Ɍv�Z�����
v(n)=v(n-1)+v(n-2)�E�E�E�B-1
u(n)=u(n-1)+u(n-2)�E�E�E�C-1
�����
F(n)=f(n)+g(n)+v(n)+u(n)=f(n-1)+f(n-2)+g(n-1�j+g(n-2)+v(n-1)+v(n-2)+u(n-1)+u(n-2)
=(f(n-1)+g(n-1�j+v(n-1)+u(n-1))+(f(n-2)+g(n-2�j+v(n-2)+u(n-2))=F(n-1)+F(n-2)�E�E�E�E�D-1
���̂��Ƃɂ��@�`�D�܂ł����ׂăt�B�{�i�b�`����ɂȂ邱�Ƃ�������܂����B
���߂����̂�15���ڂ̏ꍇ�̐��Ȃ̂�F(15)
�t�B�{�i�b�`����̈�ʍ��́Am=0,1,2�E�E�E����0��2��1�ƒ�`����Ǝ��̂悤�ɋ��߂��܂��B
�i��m-�i-��-m�j�j/��5:��=�i1+��5�j/2
�ł���F(n)�̏�����2��2����3�Ȃ̂�n=m-2�Ōv�Z���邱�ƂɂȂ�܂��B
�̂ɂ����ڂ̏ꍇ�̐�
F(n)=�i��n+2-�i-��-n-2�j�j/��5:��=�i1+��5�j/2
F(15)=1597�E�E�E�E�E��
���z
�ꍇ�̐����A����ɂȂ����Ă���Ƃ����̂͐V�N�ȋ����ł���
�܂��A�s���i������́j�Ɍ����Ƃ̌q������B
���݂ɐ搶�Ɏ����Ă����������ƌ��т����
F(n)=�i��n+2-�i-��-n-2�j�j/��5�@�@�@:��=�i1+��5�j/2
�@�@=��i=0��(n+1)/2(n+1-i�bi) :n�͊
�����藧�������ł��B
���܂ŃR���r�l�[�V�����̐���̑��a�ȂǍl�������Ƃ��Ȃ������̂ł����A�����ς���ƈӊO�Ȍ��ʂ������邱�ƂɊ������܂����B
�����̗���F���Q�̉�
���i�����̐��j�ŏꍇ�������܂��B �i�ł��A�����l���ł����j
�������i�����O�j�̂Ƃ��A���i�P�T�|���j�ł��B
�������A�����X�̂Ƃ��́A���炩�ɕs�K�B
1.
�����O�̂Ƃ��A���݂̂łP�ʂ�
2.
�����O�̂Ƃ��A�~�̋N���肤����́����[�y�ъԂ�
�@�@�@�@�P�T�|���{�P���P�U�|��
�@�@�@����āA���̋N�������16-k�bk�i�����P�C�Q�C�R�C�E�E�E�C�W�j
���������āA���̑�����
�@�P�{15�b1�{14�b2�{13�b3�{12�b4�{�E�E�E�{9�b7�{8�b8
���P�T�X�V�@�ƂȂ�܂��B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
