�����Q�U�N�T���P�P��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��305�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF�S��13���`�T��11����
�m����ȕ����W���n
���̈قȂ�v�f����Ȃ�W����S�Ƃ���BS�̂Q�̕����W���̑g�i�����ł��悢�j�ŁA���̘a�W����S�ɂȂ�悤�Ȃ��͉̂��g���邩�B���̖��ɓ�����B
�������A���Ԃ�ς��������̂��̂͋�ʂ��Ȃ����̂Ƃ���B�܂�A{�P,�Q},{�P,�R,�S}��,{�P,�R,�S}�A{�P,�Q}�͓������̂Ƃ��Đ�����B�܂��AS�̕����W���̒��ɂ͋�W�����l����B�܂��A�����P�̂Ƃ���{�P}�C{�P}��{�P}�C�ӂ�2�g�Ɛ����܂��B
���P�F�����Q�A�R�Ƃ����g���邩�����Ă݂Ă��������B
���Q�F��ʂ̏ꍇ���g�ł��邩���ŕ\���Ă��������B
NO1�uuchinyan�v
�@�@�@ 04/13 13��11���@��M �X�V 05/11
��ɂ���悤�ɁCS =
{1, 2, 3, ..., n} �Ƃ��Ĉ�ʐ�������Ȃ��̂ŁC�ȉ��ł͂������܂��B
���P�F
n = 1 �̏ꍇ
S = {1}�C�����W���C�ӁC{1}
�� �� ��
---> NG
�� �� {1}
---> OK
{1} �� {1} ---> OK
2 �g
n = 2 �̏ꍇ
S = {1, 2}�C�����W���C�ӁC{1}�C{2}�C{1, 2}
�� �� ��
---> NG
�� �� {1}
---> NG
�� �� {2}
---> NG
�� �� {1, 2}
---> OK
{1} �� {1} ---> NG
{1} �� {2} ---> OK
{1} �� {1, 2} ---> OK
{2} �� {2} ---> NG
{2} �� {1, 2} ---> OK
{1, 2} �� {1, 2} ---> OK
5 �g
n = 3 �̏ꍇ
S = {1, 2,
3}�C�����W���C�ӁC{1}�C{2}�C{3}�C{1, 2}�C{1, 3}�C{2, 3}�C{1, 2, 3}
�� �� ��
---> NG
�� �� {1}
---> NG
�� �� {2}
---> NG
�� �� {3}
---> NG
�� �� {1, 2}
---> NG
�� �� {1, 3}
---> NG
�� �� {2, 3}
---> NG
�� �� {1, 2,
3} ---> OK
{1} �� {1} ---> NG
{1} �� {2} ---> NG
{1} �� {3} ---> NG
{1} �� {1, 2} ---> NG
{1} �� {1, 3} ---> NG
{1} �� {2, 3} ---> OK
{1} �� {1, 2, 3} ---> OK
{2} �� {2} ---> NG
{2} �� {3} ---> NG
{2} �� {1, 2} ---> NG
{2} �� {1, 3} ---> OK
{2} �� {2, 3} ---> NG
{2} �� {1, 2, 3} ---> OK
{3} �� {3} ---> NG
{3} �� {1, 2} ---> OK
{3} �� {1, 3} ---> NG
{3} �� {2, 3} ---> NG
{3} �� {1, 2, 3} ---> OK
{1, 2} �� {1, 2} ---> NG
{1, 2} �� {1, 3} ---> OK
{1, 2} �� {2, 3} ---> OK
{1, 2} �� {1, 2, 3} ---> OK
{1, 3} �� {1, 3} ---> NG
{1, 3} �� {2, 3} ---> OK
{1, 3} �� {1, 2, 3} ---> OK
{2, 3} �� {2, 3} ---> NG
{2, 3} �� {1, 2, 3} ---> OK
{1, 2, 3} �� {1, 2, 3} ---> OK
14 �g
n = 3 �̏ꍇ������ƕ�����܂����C���̂悤�ɂ��Đ�����͕̂s�\�ł͂Ȃ����̂̂Ȃ��Ȃ���ςł��B
�����ŁCn = 3 �̏ꍇ�ŁC����������ς��Đ����Ă݂܂��B
A�CB �� S = {1, 2, 3} �̕����W���Ƃ��CA��B = S �Ƃ�������̂ŁC
S �̊e�v�f�� A �� B �ɐU�蕪����C�ƍl���܂��B
1 �� A ���� B �ɑ��݂�������C�����ɑ��݂��Ă������C�̂ŁC���̐U�蕪������ 2^2 - 1 = 3 �ʂ�B
2�C3 �����l�� 3 �ʂ肸�B
�����őS�̂͂����̐ςɂȂ�܂����CA �� B �����ւ������͓̂����Ƃ���̂ŁC
A = B ���� A��B = S�C�܂� A = B =
S�C�ȊO�͔����ɂ���K�v������܂��B
�����ŁC(3^3 +
1)/2 = 28/2 = 14 �g�C�ɂȂ�܂��B
���̍l�����͈�ʉ����e�Ղł��B
���Q�F
���P�F�̍Ō�̂悤�ɍl���܂��B
A�CB �� S = {1, 2, 3, ..., n} �̕����W���Ƃ��CA��B = S �Ƃ�������̂ŁC
S �̊e�v�f�� A �� B �ɐU�蕪����C�ƍl���܂��B
1 �� A ���� B �ɑ��݂�������C�����ɑ��݂��Ă������C�̂ŁC���̐U�蕪������ 2^2 - 1 = 3 �ʂ�B
2�C3�C�c�Cn �����l�� 3 �ʂ肸�B
�����őS�̂͂����̐ςɂȂ�܂����CA �� B �����ւ������͓̂����Ƃ���̂ŁC
A = B ���� A��B = S�C�܂� A = B =
S�C�ȊO�͔����ɂ���K�v������܂��B
�����ŁC(3^n +
1)/2 �g�C�ɂȂ�܂��B
(�ʉ�)
�Q�����ōl���܂��B
A�CB �� S = {1, 2, 3, ..., n} �̕����W���� A��B = S �̏ꍇ�� a(n) �ʂ�Ƃ��C
���̏ꍇ�� n+1 ��t�������܂��B
�t���������́CA �ɕt��������CB �ɕt��������CA �� B �̗����ɕt��������C�� 3 �ʂ肪�\�ł����C
A = B ���� A��B = S�C�܂� A = B =
S�C�̂Ƃ������́C�Е������ɕt��������̂͏d�����Ă��܂��̂ŁC
���̕��������܂��B�����ŁC
a(n+1) = 3
* a(n) - 1�Ca(1) = 2
�ł��B����������ƁC
a(n+1) -
1/2 = 3(a(n) - 1/2)
a(n) - 1/2
= 3(a(n-1) - 1/2) = �c = 3^(n-1) * (a(1) - 1/2) = 3^(n-1) *
(2 - 1/2) = 3^n/2
a(n) =
(3^n + 1)/2
�����ŁC(3^n +
1)/2 �g�C�ɂȂ�܂��B
(���z)
�ŏ��C�n���ɒ��ׂĂ����ƁC����ւ��ē������̂������̂���₱�������ŁC
�ǂ��������̂��C�Ǝv�����̂ł����C�ӂƁC���P�F�̍Ō�̍l�������v���t���C
�Ȃ������C�Ƃ��������ł��� (^^;
�Q�����͊m�F�Ƃ��������Œlj����܂����B
NO2�u�Ӱ��݁v
04/14 20��04���@��M �X�V 05/11
������ʔ������Ń`�������W��
���P�F�����Q�A�R�Ƃ����g���邩�����Ă݂Ă��������B
n=2 �̂Ƃ��c
(1,2)-(1,2),(0)
(1,2)-(1)
(1,2)-(2)
(1)-(2)
�܂�c5�g
n=3 �̂Ƃ��c
(123)-(123), (0)
(123)-(1),(2),(3)
(123)-(12),(23),(13)
(12)-(23)
(12)-(13)
(13)-(23)
(12)-(3)
(13)-(2)
(23)-(1)
(1)-(1),(1)-(0)
(12)-(12),(12)-(1)
(12)-(0),(12)-(2)
(1)-(2)
�܂�c14�g
���Q�F��ʂ̏ꍇ���g�ł��邩���ŕ\���Ă��������B
�\���I�ɂ́c���������Ȃ�2�{�ɑ����A�c���3�{������c
���̂Ƃ��A���������g�͏��1�g�Ȃ̂Łc
f(1)=2
f(2)=2*1+3*(f(1)-1)
f(3)=2*1+3*(f(2)-1)
f(k)=3*f(k-1)-1
f(k)-a=3*(f(k-1)-a)
2a=1
f(k)-1/2=3*(f(k-1)-1/2)
�܂�c
f(n)-1/2=3^(n-1)*(f(1)-1/2)=3^(n-1)(3/2)
f(n)=(3*3^(n-1)+1)/2
�ł悳�����ł��ˁ�
NO3�u��x�Ђ����v 04/16 00��53���@��M �X�V 05/11
���1:
n=2�̂Ƃ��A5�g�@(��)
{��,{1,2}}, {{1},{2}}, {{1},{1,2}}, {{2},{1,2}},
{{1,2},{1,2}}.
n=3�̂Ƃ��A14�g (��)�@
{��,{1,2,3}}, {{1},{2,3}}, {{2},{1,3}}, {{3},{1,2}},
{{1},{1,2,3}},
{{2},{1,2,3}}, {{3},{1,2,3}}, {{1,2},{1,3}},
{{1,2},{2,3}}, {{1,3},{2,3}},
{{1,2},{1,2,3}}, {{1,3},{1,2,3}}, {{2,3},{1,2,3}},
{{1,2,3},{1,2,3}}.
���2:
��ʉ����čl���Ă݂܂��B
n,m�𐳐����Ƃ��܂��B
n �̈قȂ�v�f����Ȃ�W����S�Ƃ��܂��B
S�� m �̕����W���̑g(�������̂������Ă��悢)�ŁA���̘a�W����S�ɂȂ�悤�Ȃ��̂̑g�̑�����A(n,m)�Ƃ��܂��B
�������A���Ԃ�ς��������̂��̂͋�ʂ��Ȃ����̂Ƃ��A�܂�S�̕����W���̒��ɂ͋�W�����l������̂Ƃ��܂��B
A(n,m)�����߂܂��B
S��n�̗v�f�̂����A�����k�̗v�f���܂܂Ȃ��悤��S�̕����W���͑S����2^(n-k)����܂��B
����2^(n-k)�̕����W���̒�����A�d����������m�̕����W�������o�����@�́A
comb(2^(n-k)+m-1,m)�ʂ肠��܂��B
�܂������k�̗v�f�̑I�т����́Acomb(n,k)�ʂ肠��܂��B
��������g���AA(n,m)�̎��͎��̂悤�ɂȂ�܂��B
A(n,m)=��[k=0�`n]((-1)^k)*comb(n,k)*comb(2^(n-k)+m-1,m)
=(1/m!)*��[p=0�`m]��[h=0�`m-p]��[j=0�`h]((2^(p*n))*((1-1/(2^p))^n)*((-1)^(m+p+j+h))*comb(h,j)*comb(m-1+h,m-p+h)*comb(2*m-p,m-p-h)*(h-j)^(m-p+h))/h!
m�̒l����̓I�ɗ^����AA(n,m)�� n �����̎��ɂȂ�܂��B
m=1,2,3,�c,10 �ɑ���
A(n,m)�̎��͎��̂悤�ɂȂ�܂����B
A(n,1)=1,
A(n,2)=(3^n + 1)/2,
A(n,3)=(7^n+3^(n+1)+2)/6,
A(n,4)=(6*7^n+15^n+11*3^n+6)/24,
A(n,5)=(31^n+5*7^(n+1)+2*3^n*5^(n+1)+50*3^n+24)/120,
A(n,6)=(15*31^n+7^n*(3^(2*n)+225)+17*3^n*5^(n+1)+274*3^n+120)/720,
A(n,7)=(127^n+175*31^n+7^(n+1)*(3^(2*n+1)+232)+49*15^(n+1)+196*3^(n+2)+720)/5040,
A(n,8)=(28*127^n+1960*31^n+255^n+7^(n+1)*(46*3^(2*n)+1876)+6769*15^n+484*3^(n+3)+5040)/40320,
A(n,9)=(546*127^n+511^n+22449*31^n+4*3^(n+2)*85^n+7^n*(56*3^(2*(n+2))+118124)+2492*3^(n+3)*5^n+12176*3^(n+2)+40320)/362880,
A(n,10)=(9450*127^n+45*511^n+31^n*(33^n+269325)+58*15^(n+1)*17^n+7^n*(21091*3^(2*n+1)+1172700)+144736*3^n*5^(n+1)+114064*3^(n+2)+362880)/3628800.
NO4�u�l�c�����v
04/17 12183���@��M �X�V 05/11
�ŏ��ɖ��Q�������D
�@�P�`���̂��̐����C�o�C�p�̂Q�̃O���[�v�ɕ�����D
�@�P�́C�o�݂̂ɓ��邩�C�p�݂̂ɓ��邩�C�o�C�p�̗����ɓ��邩�̂R�ʂ�D
�@�Q�`�������l�ɂR�ʂ�D
�@�̂ɑS���ŁC�d�����܂߂ĂR���ʂ肠��D
�@�P�`�������ׂĂo�C�p�̗����ɓ���ꍇ�ȊO�͏d�����Ă���̂ŁC�ꍇ�̐��́C
�@�@(�R���|�P)�^�Q�{�P�ʂ�
�@����͂����P�̂Ƃ��C�Q�ʂ�ƂȂ�C��̓��ƍ����D
�@���ɖ��P�ɂ��āD
�@�����Q�̂Ƃ��C(�R�Q�|�P)�^�Q�{�P���T�i�ʂ�j
�@�����R�̂Ƃ��C(�R�R�|�P)�^�Q�{�P���P�S�i�ʂ�j
�@�G�N�Z���̃}�N���Ō����Ă݂��D����ɂ��ƁC
�@�����P�̂Ƃ��C�Q
�@�����Q�̂Ƃ��C�T
�@�����R�̂Ƃ��C�P�S
�@�����S�̂Ƃ��C�S�P��(�R�S�|�P)�^�Q�{�P
�@�����T�̂Ƃ��C�P�Q�Q��(�R�T�|�P)�^�Q�{�P
�@�����U�̂Ƃ��C�R�U�T��(�R�U�|�P)�^�Q�{�P
�@�����V�̂Ƃ��C�P�O�X�S��(�R�V�|�P)�^�Q�{�P
�@�����W�̂Ƃ��C�R�Q�W�P��(�R�W�|�P)�^�Q�{�P
�ƂȂ�C���ۂ̏ꍇ�ƍ����D
�i�}�N���j
Option Explicit
Const nmax As Integer = 8
Dim a(nmax) As Integer, n As Integer
Sub Macro1()
For n = 1 To nmax
Cells(1, 4 * n - 3).Value = n: Cells(2, 4
* n - 3).Value = 0
Columns(retsu(4 * n - 2) &
":" & retsu(4 * n - 1)).Select
ActiveWindow.SmallScroll ToRight:=1
Selection.NumberFormatLocal =
"@"
Call saiki(1)
If n >= 5 Then
Columns(retsu(4 * n - 2) &
":" & retsu(4 * n - 2)).Select
Columns(retsu(4 * n - 2) &
":" & retsu(4 * n - 1)).EntireColumn.AutoFit
End If
Next n
End Sub
Sub saiki(ByVal m As Integer)
Dim P As String, Q As String
Dim deta As Integer, j As Integer
a(m) = 1 '1:P, 2:Q, 3:PQ
While a(m) <= 3
If m < n Then
Call saiki(m + 1)
Else
P = "": Q =
""
For j = 1 To n
Select Case a(j)
Case
1: P = P + Str(j)
Case
2: Q = Q + Str(j)
Case
Else: P = P + Str(j): Q = Q + Str(j)
End Select
Next j
deta = 0: j = 1
While deta = 0 And j <=
Cells(2, 4 * n - 3).Value
If (P = Cells(j, 4
* n - 2).Value And Q = Cells(j, 4 * n - 1).Value) Or (P = Cells(j, 4 * n -
1).Value And Q = Cells(j, 4 * n - 2).Value) Then
deta =
1
Else
j = j
+ 1
End If
Wend
If deta = 0 Then
Cells(2, 4 * n -
3).Value = Cells(2, 4 * n - 3).Value + 1
Cells(Cells(2, 4 *
n - 3).Value, 4 * n - 2).Value = P
Cells(Cells(2, 4 *
n - 3).Value, 4 * n - 1).Value = Q
End If
End If
a(m) = a(m) + 1
Wend
End Sub
Private Function retsu(ByVal m As Integer) As String
retsu = ActiveSheet.Cells(1, m).Address(False, False)
retsu = Left(retsu, Len(retsu) - 1)
End Function
NO5�u���N���̂�������v
04/18 09��03���@��M �X�V 05/11
��305��@���N���̂�������
�����炩���߂��ƂŎg�������m�F���Ă����܂��B
�E![]()
�@����́A�v�f�����̏W���̕����W���̌����l����ƕ�����₷���Ǝv���܂��B
�@�����W���͗v�f�̌���0����n�̂��̂܂ł���܂��B
1��1�̗v�f����݂�ƁA�����W���̗v�f�ɂȂ邩�Ȃ�Ȃ����̂ǂ��炩�ł��B
�E![]()
�@���ɁA����2�̂Ƃ��́A![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�@����́A�藝����ȒP�Ɋm�F�ł��܂��B
���1
�r2���o1,2�p�̕����W���̌��́A22��4�ł��B
�r3���o1,2,3�p�̕����W���̌��́A23��8�ł��B
�X���W���ӂ�0�A�o1,2�p��12�Ȃǂƕ\�����Ƃɂ��܂��B
���̕\���A����2�̂Ƃ���5�g�A����3�̂Ƃ���14�g����܂��B
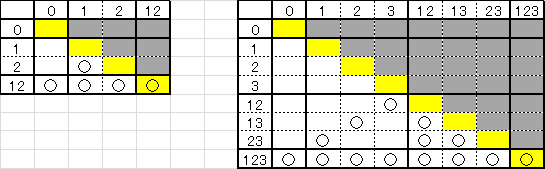
�D�F�̕����́A�Ώ̐����獶���Ɠ����Ȃ̂Ő����܂���B
���2
����4�i�r4���o1,2,3,4�p�j�̂Ƃ��ׂ邱�ƂŁA��ʂ̏ꍇ�̎肪����ɂ��܂��B
�͂��߂́A�Ώ̐������āA�Ƃɂ����a�W�����S�̏W���r4�ɂȂ���ׂ̂܂��B
�\�̍����̕����𐔂���Ɠ����́A41�g�ł��B
�Ώ̂̒��S�i���F�̕����j�ɂ���̂�1�g�����ł��B
�l�����Ƃ��ẮA�\�S�̂̑g����1�������Ĕ����ɂ��܂��B
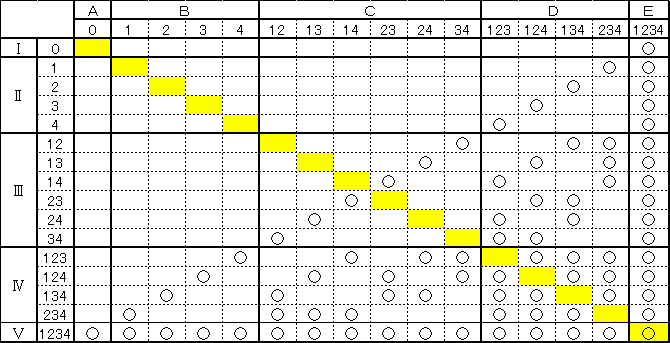
�����āA�Ⴆ�Ε\�̏ォ��W�i�ڂ̕��������Ă݂܂��B
�@���̏W���̗v�f�̌���4�Ȃ̂ŁA�v�f��3�̕����W���́A4�b3��4����܂��B
�@�@�o1,2,3�p�A�o1,2,4�p�A�o1,3,4�p�A�o2,3,4�p
�E������a�Ԗڂ̂Ƃ���ɊY������g��4����܂��B
�@�����́A�݂��ɕ�W���̊W�ɂ�����̂̃y�A�ł��B
�@�@�o1,2,3�p�Ɓo4�p�A�@�o1,2,4�p�Ɓo3�p�A�@�o1,3,4�p�Ɓo2�p�A�@�o2,3,4�p�Ɓo1�p
�@4�~1��4�b3�~3�b0�ƍl���܂��B(3�b0�́A�]���ɗv�f�����Ȃ��Ƃ����Ӗ��ł�)
�E������b�Ԗڂ̂Ƃ���ɊY������g��12����܂��B
�@�Ⴆ�A�o1,2,3�p�Ƒg�ނ��Ƃ��ł���̂́A4�Ǝc��1,2,3�̒�����1�����I�v�f����ł��镔���W���ł��B
�@���̂悤�ɍl���āA
�@�@�o1,2,3�p�Ɓo1,4�p���o2,4�p���o3,4�p�A�@�o1,2,4�p�Ɓo1,3�p���o2,3�p���o3,4�p�A
�o1,3,4�p�Ɓo1,2�p���o2,3�p���o2,4�p�A�@�o2,3,4�p�Ɓo1,2�p���o1,3�p���o1,4�p
�@12��4�~3��4�b3�~3�b1�ƍl���܂��B
�E������c�Ԗڂ̂Ƃ���ɊY������g��12����܂��B
�@�Ⴆ�A�o1,2,3�p�Ƒg�ނ��Ƃ��ł���̂́A4�Ǝc��1,2,3�̒�����2�����I�v�f����ł��镔���W���ł��B
�@���̂悤�ɍl���āA
�@�@�o1,2,3�p�Ɓo1,2,4�p���o1,3,4�p���o2,3,4�p�A�@�o1,2,4�p�Ɓo1,2,3�p���o1,3,4�p���o2,3,4�p�A
�o1,3,4�p�Ɓo1,2,3�p���o1,2,4�p���o2,3,4�p�A�@�o2,3,4�p�Ɓo1,2,3�p���o1,2,4�p���o1,3,4�p
�@12��4�~3��4�b3�~3�b2�ƍl���܂��B
�E������d�Ԗڂ̂Ƃ���ɊY������g��4����܂��B
�@�Ⴆ�A�o1,2,3�p�Ƒg�ނ��Ƃ��ł���̂́A4�Ǝc��1,2,3�̒�����3�����I�v�f����ł��镔���W���ł��B
�@���̂悤�ɍl���āA
�@�@�o1,2,3�p�Ɓo1,2,3,4�p�A�@�o1,2,4�p�Ɓo1,2,3,4�p�A
�@�o1,3,4�p�Ɓo1,2,3,4�p�A�@�o2,3,4�p�Ɓo1,2,3,4�p
�@4��4�~1��4�b3�~3�b3�ƍl���܂��B
�E�ȏォ��W�i�ڂ̍��v�́A
4�{12�{12�{4��4�~1�{4�~3�{4�~3�{4�~1��4�~(1�{3�{3�{1)��4�b3�~(3�b0�{3�b1�{3�b2�{3�b3)
�ƍl���܂��B
�����̂悤�ɇT�i�ڂ���l���Ă����ƁA
�E�T�i�ڂ́A4�b0�~0�b0
�E�U�i�ڂ́A4�b1�~(1�b0�{1�b1)
�E�V�i�ڂ́A4�b2�~(2�b0�{2�b1�{2�b2)
�E�W�i�ڂ́A4�b3�~(3�b0�{3�b1�{3�b2�{3�b3)
�E�X�i�ڂ́A4�b4�~(4�b0�{4�b1�{4�b2�{4�b3�{4�b4)
���ȏ���܂Ƃ߂�ƁA
�@�@4�b0�~0�b0�{4�b1�~(1�b0�{1�b1)�{4�b2�~(2�b0�{2�b1�{2�b2)
�{4�b3�~(3�b0�{3�b1�{3�b2�{3�b3)�{4�b4�~(4�b0�{4�b1�{4�b2�{4�b3�{4�b4)
��![]()
�@�ȏォ��A����4�̂Ƃ��́A![]() �g�ł��B
�g�ł��B
�����̍l���������̏ꍇ�ɂ��Ă͂߂�ƁA
�@�@![]()
�ƂȂ�܂��B
�u���N���̂�������v 04/27 08��10���@��M �X�V 05/11
��305��i���̂Q�j�@
�����̍l�����́A�v�f�����̏W���̕����W���̌��̐������Ǝ��Ă��܂��B
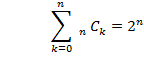
�@�����W���͗v�f�̌���0����n�̂��̂܂ł���܂��B
1��1�̗v�f����݂�ƁA�����W���̗v�f�ɂȂ邩�Ȃ�Ȃ����̂ǂ��炩�ł��B
���r��2�̕����W����A�AB�Ƃ��܂��B
�a�W��![]() ���r�ɂȂ�Ƃ������Ƃ́A�v�fs����݂�ƁA
���r�ɂȂ�Ƃ������Ƃ́A�v�fs����݂�ƁA
(1)![]() �i����B�ł͂Ȃ��j�@�@(2)
�i����B�ł͂Ȃ��j�@�@(2)![]() �i����A�ł͂Ȃ��j�@�@(3)
�i����A�ł͂Ȃ��j�@�@(3)![]()
��3�̂ǂꂩ���Ȃ肽�Ƃ������Ƃł�
�E![]() �̂Ƃ��́A���e�I�ɂ͓����y�A��2�g�l�����܂��B
�̂Ƃ��́A���e�I�ɂ͓����y�A��2�g�l�����܂��B
�@�iA��B�j�́iB��A�j�Ɠ����ł��B
�@���g���������̂͋�ʂ��܂���B
�E![]() �̂Ƃ��́A1�g��������܂���B
�̂Ƃ��́A1�g��������܂���B
�l�����Ƃ��ẮA�S�̂̑g����1�������Ĕ����ɂ��܂��B
�����̍l���������̏ꍇ�ɂ��Ă͂߂�ƁA
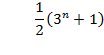
�ƂȂ�܂��B
�u���N���̂�������v 04/28 21��01���@��M
�X�V 05/11
��305��i���̂R�j�@���Q������p���čl���܂��B
���̈قȂ�v�f����Ȃ�W�����rn�Ƃ��A�rn��2�̕����W���̑g�ŁA���̘a�W�����rn�ɂȂ�悤�Ȃ��̂̑g����an�Ƃ��܂��B
a1��2�ł��B�i��1�̉����Aa2��5�Aa3��14�ł��j
���rn�̏ꍇ�̑g�̈����X�I�ɂ`�O���[�v�A����������a�O���[�v�Ƃ��܂��B�i�ǂ�����`�A�a�ɂ��邩�͔C�ӂł��܂��܂���j
�@�rn+1�̏ꍇ���rn�̂Ƃ��̑g�����Ƃɂ��čl���܂��B
�@�rn+1�̑g�́A���̎葱���̂ǂꂩ�ɂȂ�܂��B
(1)�rn�̂Ƃ��̂`�O���[�v�̗v�f�Ɂon+1�p��t������������
(2)�rn�̂Ƃ��̂a�O���[�v�̗v�f�Ɂon+1�p��t������������
(3)�rn�̂Ƃ��̂`�A�a�����̃O���[�v�̗v�f�Ɂon+1�p��t������������
�E�rn�̑g�Ɂon+1�p��t��������̂ŁA���̎葱���̂��Ƒg�Ƃ��ē����ɂȂ���͎̂���1�g�����ł��B
�`�A�a�O���[�v�Ƃ����̏W���rn�̂Ƃ�����(1)��(2)�̎葱����A�g�Ƃ��ē����ɂȂ�܂��B(���Ԃ��1�g�����ł�)
�E�rn�̏ꍇ�̑g�ɂ��ꂪ�Ȃ���A�rn+1�̑g�ɂ��A����͂���܂���B
�rn+1�̑g�ɂ��ꂪ�������Ƃ��܂��B
���ꂽ�g�̗v�f�������o���܂��B
���ɁA�����̗v�f����on+1�p����菜���Ă݂܂��B
��������Ƃrn�̑g�ƂȂ�܂��B
�@����Ƃrn�̑g�̃��X�g�ɂ��ꂪ�Ȃ��̂�����A���łɂ��郊�X�g�̂ǂꂩ�ƈ�v���邱�ƂɂȂ�܂��B
�@����͂��ꂪ����Ƃ������Ƃɖ���������̂łrn+1�̑g�ɂ��A���ꂪ�Ȃ����ƂɂȂ�܂��B
������āA���̑Q���������藧���܂��B
�@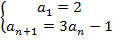
���������� ![]() �̉�
�̉�
![]() ��p���āA
��p���āA
![]()
�@�����
![]() �́A����
�́A����
![]() �A����3�̓��䐔��ƂȂ�܂��B
�A����3�̓��䐔��ƂȂ�܂��B
![]()
�@��
![]()
NO6�u�ɂ���Z12�v 05/03 00��03���@��M �X�V 05/11
���1
|
�����Q�̏ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��W���Ӂ��o�p�ɑ��Ă͂��ׂĂ̌����Ή��� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S���� =S����A�o1,2�p�݂̂ł��B�E�E�E�P�@�@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��W����1�g�̈���̏W���ƍl����Ə�L�P�g�������J�E���g����悢���ƂɂȂ�܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o1�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2�p�o1,2�p�E�E�E2�@�A-1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o2�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1�p�o1,2�p�E�E�E2�@�A-2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o1,2�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�Ӂo1�p�o2�p�o1,2�p�E�E�E4�@�B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�����ŁA�A-1.2�̃_�u�肪�A�o1�p�o2�p��1�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�B���@�A�ƃ_�u��̂̓Ӂo1,2�p�A�o1�p�o1,2�p�A�o2�p�o1,2�p��3�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�����1+2+2+4-1-3��5�E�E�E�E�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
����� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�Ӂo1,2�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1�p�o2�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1�p�o1,2�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2�p�o1,2�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,2�p�o1,2�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�ƂȂ�܂��B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
����3�̏ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��W���Ӂ��o�p�ɑ��Ă͂��ׂĂ̌����Ή��� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S���� =S����A�o1,2,3�p�݂̂ł��B�E�E�E�P�@�@-1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o1�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2,3�p�o1,2,3�p�E�E�E2�@�A-1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o2�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,3�p�o1,2,3�p�E�E�E2�@�A-2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o3�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,2�p�o1,2,3�p�E�E�E2�@�A-3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o1,2�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o3�p�o2,3�p�o1,3�p�o1,2,3�p�E�E�E4�@�B-1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o1,3�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2�p�o1,2�p�o2,3�p�o1,2,3�p�E�E�E4�@�B-2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o2,3�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1�p�o1,2�p�o1,3�p�o1,2,3�p�E�E�E4�@�B-3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���ɕ����W���o1,2,3�p�ɂ��čl����Ƙa�W����S�ƂȂ�̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�Ӂo1�p�o2�p�o3�p�o1,2�p�o1,3�p�o2,3�p�o1,2,3�p�E�E�E8�@�C |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�����ŁA�A�ƇB�̃_�u�肪�A�o1�p�o2,3�p�A�o2�p�o1,3�p�A�o3�p�o1,2�p�A�o1,2�p�o2,3�p�A�o1,2�p�o1,3�p�A�o1,3�p�o2,3�p�A��6�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�C���@�A�B�ƃ_�u��̂́o1,2,3�p�o1,2,3�p�ȊO�̂�7�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�����1+2+2+2+4+4+4+8-6-7��14�E�E�E�E�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
����� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�Ӂo1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1�p�o2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2�p�o1,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o3�p�o1,2�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o3�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,2�p�o1,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,2�p�o2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,2�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,3�p�o2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,3�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o2,3�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�o1,2,3�p�o1,2,3�p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�ƂȂ�܂��B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n�̌����l����ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��P�g���W���h�Ƃ��A���̕�W�����h�f�Ƃ��܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��Q�g���W��P�Ƃ����̕�W����P�f�Ƃ��܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
��1�g�Ƒ�2�g�̐ϏW����K�Ƃ��܂��iK=I��P�j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S=P'��K��I'�@P'��K=�Ӂ@�@K��I'=�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I=K��P'�@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P=K��I'�@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�����܂���ƏW��I�ƏW��P�͓����i���j�ł��邽��I����肤��W���͂��ׂ�P����肤�鎖������܂��B�E�E�E�E�iA) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̏ꍇ�̐����v�Z���܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̏ꍇ�̌��E�E�E�E�E�A |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K��I�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̌���0�̏ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
nC0=1 K=�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̌����P�̏ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
nC1=n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̌���2�̏ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
nC2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̌���i�̏ꍇ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
nCi |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̌���n�̏ꍇ�iK'=��) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
nCn=1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�������킹��� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Km=��i=0��n nCi |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���̂R�̏W�����l���܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P�f�AK�AI�f |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K��i�̌������ꍇ��K�̌�����肤��ꍇ�̐��͏�L���� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
nCi |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
����ŁA���̎�P�f��n-i��K�ƈقȂ錳����������̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P�f�̎������錳�̌���n-i�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P'��n-i�̌������ꍇ��P'�̌�����肤��ꍇ�̐�(�ӂ��܂�)�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P'mi=��j=0��n-i n-iCj |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�ȏォ��P'�̎�肤��ꍇ�̐��� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P'm��i=��j=0��n-i i=0��n�@ n-iCj�EnCi |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�ƂȂ�܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�܂��A |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P'mi=��j=0��n-i n-iCj |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�͓W���̑��a�ɓ������̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�i1+1�jn-i��2n-i �ɓ����� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
����� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�㎮��nCi���܂�2���W���Ȃ̂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���̎��́A�i2+1�j����3�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�Ə������Ƃ��ł��܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
�����ŁA�iA�j����AI'��P'�����ւ������̂��P�Ƃ��ăJ�E���g����Ƃ����������l���܂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
K�̏W���ɑΉ�����P'�̏W���́iA)����I'�ɂ����݂��ꍇ�̐���1/2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�ɂȂ�܂��B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�������AK��S�̏ꍇ�ɂ̂�P'=I'=�ӂƂȂ�ꍇ�̐���1�ƂȂ�܂��B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���������ċ��߂�g�ݍ��킹�̐���Sm�Ƃ���� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Sm=�i3n+1�j/2�E�E�E�E�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
