�����Q�U�N�X���Q�P��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��311�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF�W��31���`9��21����
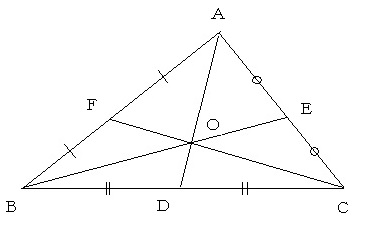
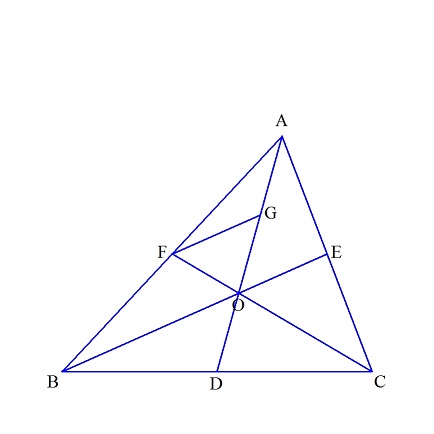
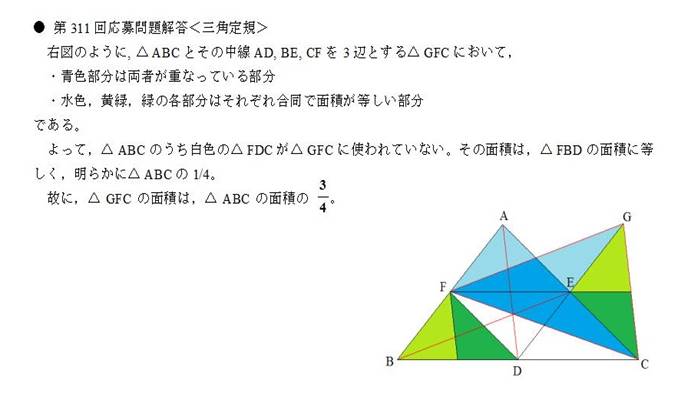
�m3�ӂ������̒����n
�@�O�p�`�`�a�b��3�{�̒����`�c�C�a�d�C�b�e��3�ӂƂ���O�p�`�̖ʐς́A���Ƃ̎O�p�`�`�a�b�̉����̂����ɂȂ邩�B
NO1�uuchinyan�v
�@�@�@ 08/31 16��39���@��M
�uuchinyan�v �@�@�@ 09/01 13��06���@��M
�X�V 09/21
�ȉ��ł́C�����̕X��C
�R�ӂ��R�{�̒��� AD�CBE�CCF �̒����ł���O�p�`���C
�K���ɓ_ X�CY�CZ �����C��XYZ�CXY = AD�CYZ = BE�CZX =
CF�C�Ƃ��Ă����܂܂��B
(��@1)�@�������̂P
�܂��C�悭�m���Ă���悤�ɁCAD�CBE�CCF �͈�_�Ō���肻�̌�_ O �� ��ABC �̏d�S�C�ł��B
�����ŁCO �� AD�CBE�CCF�� 2�F1 �ɓ������܂��B
E �𒆐S�� ��AOC �� 180����]�� O �̈ړ���� O' �Ƃ��܂��B
AE = CE �Ȃ̂ŁCA �� C �ɁCC �� A �ɏd�Ȃ�COE = O'E �ŁCO�CE�CO' �͓��꒼����ɂ���C
��AOCO' �͕��s�l�ӌ`�ɂȂ��āCE �͑Ίp�� AC OO' �̌�_�ɂȂ�܂��B
�����ŁCOO' = OE
* 2 = BO = BE * 2/3�C�ł��B
�܂��CAO = AD *
2/3�CAO' = CO = CF * 2/3�C�Ȃ̂ŁC
��XYZ ��
��AOO' �� ������ 3/2 �Ɋg�債�����̂ŁC��XYZ = ��AOO' * 9/4�C�ł��B
����ŁC��AOO' = ��AOC = ��ABC * BO/BE = ��ABC * 1/3�C�ł��B
�����ŁC��XYZ = ��AOO' * 9/4 = ��ABC * 1/3 * 9/4 = ��ABC * 3/4�C�ł��B
�܂�C�R�ӂ��R�{�̒����̒����ł���O�p�`�̖ʐς́C���̎O�p�`�̖ʐς� 3/4 �{�ɂȂ�܂��B
�Ȃ��CA ���� CO �ɁCC ���� AO �ɂ��ꂼ�ꕽ�s�Ȑ���������_�� O' �Ƃ���C�Ƃ��C
BE �̉������ O'E = OE �ƂȂ�_ O' �����C�Ƃ��C���Ă������ł��ˁB
(��@2)�@�������̂Q
D ���� BE �ɁCE ���� BC �ɂ��ꂼ�ꕽ�s�Ȑ���������_�� P �Ƃ��܂��B
��EBDP �͕��s�l�ӌ`�Ȃ̂� DP = BE �ł��B
����ɁCEP = BD
= DC�CEP//DC �Ȃ̂� ��EDCP �����s�l�ӌ`�ŁCPC = ED�CPC//ED�C�ł��B
����ŁCCD = DB�CCE = EA �C���_�A���藝���CED = AB/2 = AF�CED//AB�C�������܂��B
�����ŁCPC = AF�CPC//AF �ƂȂ��� ��AFCP �����s�l�ӌ`�ŁCPA = CF�C�ł��B
���ǁC��ADP �́C�R�ӂ��CAD�CDP = BE�CPA = CF�C�̎O�p�`�Ȃ̂ŁC��XYZ �� ��ADP�C�ł��B
����ɁCDP �� AC �Ƃ̌�_�� Q �Ƃ���ƁCBE//DP
��� CQ�FQE = CD�FDB = 1�F1�C�ŁC
CE�FEA = 1�F1 = 2�F2 �ƍ��킹�āCCQ�FQA = 1�F3�CAQ = AC * 3/4�C�������܂��B
�����ŁCB ��� AC �ɁCD ��� P ��ʂ��� AC �ɕ��s�Ȑ��ɁC���������낵���� H�CI �Ƃ���ƁC
BE//DP�CAC//PI�C��BEH = ��DPI�C��BHE = 90��= ��DIP�CBE = DP�C��BEH �� ��DPI�CBH = DI
�����ŁC��XYZ = ��ADP = AQ * DI * 1/2 = (AC * 3/4) * BH * 1/2 = ��ABC * 3/4�C�ł��B
�܂�C�R�ӂ��R�{�̒����̒����ł���O�p�`�̖ʐς́C���̎O�p�`�̖ʐς� 3/4 �{�ɂȂ�܂��B
(��@3)�@�������̂R
AQ = AC *
3/4�C�܂ł́C(��@2)�Ɠ����B
�����ŁC���l�ɁC
E ���� CF �ɁCF ���� CA �ɂ��ꂼ�ꕽ�s�Ȑ���������_�� P'�C
F ���� AD �ɁCD ���� AB �ɂ��ꂼ�ꕽ�s�Ȑ���������_�� P''�C
�Ƃ��C���l�̎O�p�`�C��BEP'�C��CFP''�C�����CQ �ɑΉ�����_��
Q'�CQ''�C�Ƃ���ƁC
��BEP' ��
��YZX�C��CFP'' �� ��ZXY�CBQ' = BA * 3/4�CCQ''
= CB * 3/4
�ƂȂ��āC��XYZ �̂R�{�̒����̒����́CAB�CBC�CCA ���ꂼ��� 3/4 �{�ɂȂ�܂��B
�����Ă����R�{�̒����łł���O�p�`�� ��ABC �ɑ����� 3/4 �ɏk���������̂ŁC
���̖ʐς� ��ABC �� (3/4)^2 �{�ł��B
�����ŁC�P��̂R�{�̒����ŎO�p�`����鑀��Ŗʐς� k �{�ɂȂ�Ƃ���C
�Q��̑���ł� k^2 �{�ŁC���ꂪ
(3/4)^2 �{�ɓ������̂ŁCk = 3/4�C�ł��B
�܂�C�R�ӂ��R�{�̒����̒����ł���O�p�`�̖ʐς́C���̎O�p�`�̖ʐς� 3/4 �{�ɂȂ�܂��B
(��@4)�@�v�Z���
BC = a�CCA = ���CAB = c�CAD = d�CBE = e�CCF = f�C�Ƃ��܂��B
�p�b�v�X�̒����藝���C
b^2 + c^2
= 2(d^2 + (a/2)^2)�Cd^2 = (2b^2 + 2c^2 - a^2)/4
c^2 + a^2
= 2(e^2 + (b/2)^2)�Ce^2 = (2c^2 + 2a^2 - b^2)/4
a^2 + b^2
= 2(f^2 + (c/2)^2)�Cf^2 = (2a^2 + 2b^2 - c^2)/4
�����ŁC�w�����̌������C
��XYZ = ��((d + e + f)/2 * (d + e - f)/2 * (d - e + f)/2 * (- d + e + f)/2)
(4��XYZ)^2 = (d + e + f)(d + e - f)(d - e + f)(- d + e + f)
= - (d +
(e + f))(d - (e + f))(d + (e - f))(d - (e - f))
= - (d^2 -
(e + f)^2)(d^2 - (e - f)^2)
= - d^4 +
2(e^2 + f^2)d^2 - (e^2 - f^2)^2
= - ((2b^2
+ 2c^2 - a^2)/4)^2
+ 2((2c^2
+ 2a^2 - b^2)/4 + (2a^2 + 2b^2 - c^2)/4)((2b^2 + 2c^2 - a^2)/4)
- ((2c^2 +
2a^2 - b^2)/4 - (2a^2 + 2b^2 - c^2)/4)^2
= - ((2b^2
+ 2c^2 - a^2)/4)^2
+ 2((4a^2
+ b^2 + c^2)/4)((2b^2 + 2c^2 - a^2)/4)
- ((3c^2 -
3b^2)/4)^2
(16��XYZ)^2
= - (2b^2
+ 2c^2 - a^2)^2
+ 2(4a^2 +
b^2 + c^2)(2b^2 + 2c^2 - a^2)
- (3c^2 -
3b^2)^2
= - 4b^4 -
4c^4 - a^4 - 8b^2c^2 + 4a^2b^2 + 4c^2a^2
+ 16a^2b^2
+ 4b^4 + 4b^2c^2 + 16c^2a^2 + 4b^2c^2 + 4c^4 - 8a^4 - 2a^2b^2 - 2c^2a^2
- 9c^4 +
18b^2c^2 - 9b^4
= 18a^2b^2
+ 18b^2c^2 + 18c^2a^2 - 9a^4 - 9b^4 - 9c^4
=
9(2a^2b^2 + 2b^2c^2 + 2c^2a^2 - a^4 - b^4 - c^4)
= - 9(a^4 -
2(b^2 + c^2)a^2 + (b^2 - c^2)^2)
= 9(- (a^2
- (b + c)^2)(a^2 - (b - c)^2))
= 9(- (a +
(b + c))(a - (b + c))(a + (b - c))(a - (b - c)))
= 9(a + b
+ c)(a + b - c)(a - b + c)(- a + b + c)
= 9(4��ABC)^2
(16��XYZ)^2 = (12��ABC)^2
16��XYZ = 12��ABC
��XYZ = ��ABC * 3/4
�܂�C�R�ӂ��R�{�̒����̒����ł���O�p�`�̖ʐς́C���̎O�p�`�̖ʐς� 3/4 �{�ɂȂ�܂��B
(��@5)�@�x�N�g���̊O�ς̗��p
�ȉ��ł́C[a] �ȂǂŃx�N�g����\�����Ƃɂ��܂��B
�܂��C��w���x���ɂȂ�܂����C�x�N�g���̊O�ς𗘗p���܂��B
�����ŁC�x�N�g���̊O�ςƂ́C��̃x�N�g�� [a] �� [b] ����\������C
���̌����� [a] ���� [b] �Ɍ����ĉE�˂����Ƃ��ɉE�˂����i�ޕ����C
���̑傫���� [a] �� [b] �̍�镽�s�l�ӌ`�̖ʐρC
�Ƃ���x�N�g���ŁC[a]�~[b] �Ə������Ƃɂ��܂��B
[a]�~[a] = [0]�C[a]�~[b] =
- [b]�~[a]�C�ł��B
���āC[AB] =
[a]�C[AC] = [b] �Ƃ���ƁC
��ABC = ([AB]
�� [AC] �̍�镽�s�l�ӌ`�̖ʐ�)/2 = |[AB]�~[AC]|/2 = |[a]�~[b]|/2�C�ł��B
����ɁC[AF] =
[a]/2�C[AE] = [b]/2�C[BC] = [AC]
- [AB] = [b] - [a]�C�ŁC
[AD] =
[AB] + [BC]/2 = ([a] + [b])/2
[BE] = [AE]
- [AB] = (- 2[a] + [b])/2
[CF] =
[AF] - [AC] = ([a] - 2[b])/2
��XYZ �́CX = A = F�CY = D = B�CZ
= E = C�C[XY] = [AD]�C[XZ] = [FC]�C�Ƃ���悭�C
��XYZ = |[XY]�~[XZ]|/2 = |[AD]�~[FC]|/2 = |- [AD]�~[CF]|/2 = |[AD]�~[CF]|/2
= |(([a] +
[b])/2)�~(([a] - 2[b])/2)|/2 = |([a] + [b])�~([a] - 2[b])|/8
= |[a]�~[a] + [b]�~[a] - 2[a]�~[b]- 2[b]�~[b]|/8
= |[0] -
[a]�~[b] - 2[a]�~[b]- 2[0]|/8
= |- 3[a]�~[b]|/8 = |[a]�~[b]|/2 * 3/4 = ��ABC * 3/4
�܂�C�R�ӂ��R�{�̒����̒����ł���O�p�`�̖ʐς́C���̎O�p�`�̖ʐς� 3/4 �{�ɂȂ�܂��B
(���z)
�������Ă����Ɏv���t�����̂��C(��@1)��(��@5)�ł����B���̌�(��@2)���v���t���܂����B
�����C(��@1)����(��@2)�̕ӂ肪���R���ȁC�Ƃ͎v���܂������C
���s�l�ӌ`�����ȂǁC����Ȃ�ɍH�v���K�v�ł��B
���̓_�C(��@5)�́C��w���x���Ȃ̂ł��̃T�C�g�ł͈ᔽ���ȁC�Ƃ͎v�����̂́C
�\���m��������C�����H�v�͂��炸�v�Z���̂��ȒP�Ȃ̂ŁC�ꉞ�����Ă����܂����B
(��@3)��(��@1)���܂Ƃ߂Ă���Ƃ��Ɏv���t������@�ł��B
(��@1)�̕����Ő����������Ă݂�ƕ��G�ɂȂ��Ă����̂ł����C
�ꕔ��ʉ��Ƃł��邱�ƂɋC�t���C��������o���Ă܂Ƃ߂��̂�(��@2)�ł��B
�����Ď��o�����c�肪(��@3)�ł��B�A�C�f�B�A��������Ɩʔ����Ǝv���Ă��܂��B
�����܂ŏ����āC���ƂȂ���r�̂��߂ɂ��v�Z�d���̉�@���~�����Ȃ��āC
(��@4)�������Ă݂܂����B���Ɣ�ׂ�Ƒ�ςł����C�悪������̂Ŏv�������y�ł��B������ɂ���C���낢��Ɗy���߂���ł����B
NO2�u�ɂ���Z12�v
09/01 00��53���@��M �X�V 09/21
�ɂ���Z12�ł�
�}�`�̖��̖͂��͕s����i�}��`���̂Ɏl�ꔪ�ꂷ��̂Łj�ł���
���Ƃ��Ȃ肻���Ȃ̂ʼn����Ă��������܂�
�_E�ɂ��ē_�Ώ̂Ȑ}�����ƓY�t�}�ipdf�j�̂悤�ȕ��s�l�ӌ`�ɂȂ�܂�
�i��������͓Y�t�}���Q�Ƃ��Ȃ��炨�肢���܂��j
�����ŁA���߂�O�p�`��ADF�f
���̎O�p�`�̖ʐς�S�Ƃ���ƕ��s�l�ӌ`ABCB�f�̖ʐς�2S
ADF�f��2S-ABD-AF�fB�f-DCF�f
ABD��AF�fB�f��S/2
DCF�f��DCE��S/4
��ADF�f��2S-S-S/4=3S/4�E�E�E�E�E��
�i�r���̏Ɩ��͂��Ȃ�[�܂�܂������A2�Ӓ��_�A���藝�ƎO�p�`�̍������A���w�Z�̐}�`�̒P���ł��̂ł��e�͂��������j
�u�ɂ���Z12�v
09/05 00��10���@��M �X�V 09/21
�ɂ���Z12�ł�
�����藝�ƁA�w�����̕ό`�ōl���Ă��܂������A�Ȃ��Ȃ��V���v���ɍs���܂���B
��@�́i�Y�t�}�����Ԃ�s�v�ȁj�ʉ����v�����܂����B
�@OB�̒��_��G�Ƃ��܂�
�A�O�p�`�̖ʐς����̂悤�ɋL�q���܂�
ABC=AEO/6=AFO/6=BFO/6=BDO/6=CDO/6=CEO/6�@��O���d�S�ł��邱�Ƃ��疾�炩
FGO=FBO/2
�BFG��AO�ɕ��s�iAOB�ɂ����钆�_�A���藝�j
�@FG=AO/2=AD/3=OD�@��O���d�S�ł��邱�Ƃ��疾�炩
�@FO=FC/3
�@DO=DA/3
�C�B���O�p�`FGO�͒�����3�ӂƂ���O�p�`�Ƒ����ŕӒ���1/3�ʐς�1/9
�@�A���FGO��ABC/12
�D����Ē�����3�ӂƂ���O�p�`�̖ʐς�S�Ƃ����
�@S��9�~FGO��9 �~ABC/12��3/4 ABC�E�E�E�E��
NO3�u���N���̂�������v
09/01 10��02���@��M �X�V 09/21
������ ![]() �ł��B
�ł��B
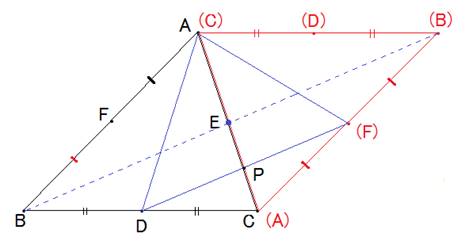
���P�i�}�`�Łj
��ABC��_E�Ɋւ���180����]���܂��B
����ƁA��ABC(B)�͕��s�l�ӌ`�ł��B
��CB(B)�ɒ��_�A���藝�����Ă͂߂�ƁA2�~D(F)��B(B)�Ȃ̂ŁAD(F)=BE�ł��B
����āA��AD(F)�͒��ڂ���O�p�`�ł��B
��AD(F)��AC��2�̕����ɕ����܂��B
���ꂼ��̎O�p�`�ɂ��āAAP���ӂƂ��Ă݂܂��B
�����́�ABC�̔����A��ӂ́�ABC��4����3�ł��B
�O�p�`�̖ʐς́A��ӂƍ����ɂ��ꂼ���Ⴗ��̂ŁA��ABC����ɂ���ƁA
![]()
���Q�i�v�Z�Łj
3�ӂ̒������킩���Ă���Ƃ��A�O�p�`�̖ʐς̓w�����̌������A
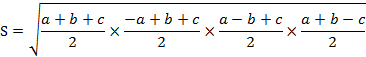
![]()
![]()
��ABC�ɒ����藝�����Ă͂߂܂��B
![]()
AB=c�AAC=b�ABC=a�AAD=d�Ƃ���ƁA
![]()
����āA
![]()
���l�ɁA
![]()
![]()
�����́Aa��b�Ab��c�Ac��a�̂悤�ɁA�����̃��[�e�[�V�����œ����܂��B
3�ӂ̒������Ad�Ae�Af�̎O�p�`�̖ʐ�S�f�́A
![]()
�����̒���2��̐ς̕����̈�́A
![]()
![]()
![]()
4��̕����̈�́A
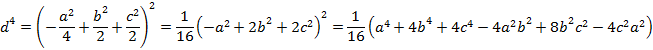
����č����̒��́A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
�ȏォ��A
![]()
![]()
![]()
NO4�u�l�c�����v
09/01 14��35���@��M �X�V 09/21
�`�c�C�a�d�̌�_���n�i�d�S�j�C�`�n�̒��_���f�Ƃ��āC�e�f�����ԁD
�@���̂Ƃ��C�d�S�̐�������C
�@�@�f�n���`�n�^�Q���`�c�^�R
�@�@�e�n���b�e�^�R
�@�܂��C�e�C�f�͂��ꂼ��`�a�C�`�n�̒��_�Ȃ̂ŁC���_�A���藝����C
�@�@�e�f���a�n�^�Q���a�d�^�R
�@�̂Ɂ��f�e�n�̂R�ӂ́C�`�c�C�a�d�C�b�e�̒������R�ӂƂ���O�p�`�s�̂R�ӂ̂P�^�R�̒�����L����D
�@�̂Ɂ��f�e�n�ƎO�p�`�s�͑����ł���C������͂P�F�R�ƂȂ�C�ʐϔ�͂P�F�X�ł���D
�@���ɁC
�@�@���f�e�n���P�^�Q�E���`�e�n���P�^�Q�E�P�^�R�E���`�e�b���P�^�U�E���`�e�b
�@�@�@�@�@�@���P�^�U�E�P�^�Q�E���`�a�b���P�^�P�Q�E���`�a�b
�@�@���O�p�`�s���X���f�e�n���X�^�P�Q�E���`�a�b���R�^�S�E���`�a�b
�@�܂��O���t�\���\�t�gGRAPES���g���āC���̐}��\�����Ă݂��D
�@�ǂ̂悤�ȁ��`�a�b��\�����Ă��C����ɑ���O�p�`�s�̖ʐϔ�͂R�^�S�ƂȂ����D
�u�l�c�����v
09/03 10��34���@��M
�u�l�c�����v
09/06 08��22���@��M �X�V 09/21
�i�ʉ��j�i�w�I�l�@�������Ȑl�p�C�����g�����ł��j
�@���������`�a�C���������`�b�C�ڂa�`�b���ƁC�r�����`�a�b�C�`�c�C�a�d�C�b�e���R�ӂ̒����Ƃ���O�p�`�̖ʐς��r'�Ƃ���D
�@�����b�����b�C�����b�����b�Ƃ���Ƃ��C
�@�@�r���P�^�Q�E�b�����b�b�����bsin�Ɓ��P�^�Q�E����sin��
�@�@���c�`���|(���`�a�{���`�b)�^�Q���|(�����{����)�^�Q
�@�@���a�d�����`�d�|���`�a�������^�Q�|������(�����|�Q����)�^�Q
�@�@���b���c�`�b�Q��(�b�����b�Q�{�Q�����E�����{�b�����b�Q)�^�S
�@�@�@�@�@�@�@�@�@��(���Q�{�Q����cos�Ɓ{���Q)�^�S
�@�@�@�b���a�d�b�Q��(�b�����b�Q�|�S�����E�����{�S�b�����b�Q)�^�S
�@�@�@�@�@�@�@�@�@��(���Q�|�S����cos�Ɓ{�S���Q)�^�S
�@�@�@���c�`�E���a�d���|(�����{����)�^�Q�E(�����|�Q����)�^�Q
�@�@�@�@�@�@�@�@�@�@��(�Q�b�����b�Q�{�����E�����|�b�����b�Q)�^�S
�@�@�@�@�@�@�@�@�@�@��(�Q���Q�{����cos�Ɓ|���Q)�^�S
�@�@���r'���P�^�Q�E{�b���c�`�b�Q�b���a�d�b�Q�|(���c�`�E���a�d)�Q}�P�^�Q
�@�@�@�@�@���P�^�Q�E[(���Q�{�Q����cos�Ɓ{���Q)�^�S�E(���Q�|�S����cos�Ɓ{�S���Q)�^�S�|{(�Q���Q�{����cos�Ɓ|���Q)�^�S}�Q]�P�^�Q
�@�@�@�@�@���P�^�W�E{(���Q�{�Q����cos�Ɓ{���Q)(���Q�|�S����cos�Ɓ{�S���Q)�|(�Q���Q�{����cos�Ɓ|���Q)�Q}�P�^�Q
�@�@���P�^�Q�����(���Q���Q�|�S���R��cos�Ɓ{�S���S�{�Q�����Rcos�Ɓ|�W���Q���Qcos�Q�Ɓ{�W���R��cos�Ɓ{���S�|�S�����Rcos�Ɓ{�S���Q���Q)
�@�@�@�@�@�@�@�@�@�@�|(�S���S�{���Q���Qcos�Q�Ɓ{���S�{�S���R��cos�Ɓ|�Q�����Rcos�Ɓ|�S���Q���Q)
�@�@�@�@�@�@�@�@���X���Q���Q�|�X���Q���Qcos�Q��
�@�@�@�@�@�@�@�@���X���Q���Qsin�Q��
�@����sin�Ɓ��O����C
�@�@�r'���P�^�W�E�R����sin�Ɓ��R�^�S�E�P�^�Q�E����sin�Ɓ��R�^�S�E�r
NO5�u�Ӱ��݁v
09/02 21��29���@��M �X�V 09/21
����́A�C�t���܂����̂ŁA�}��Y�t���ăG���g���[��
�Y�t�}�Q�Ɗ肢�܂��B
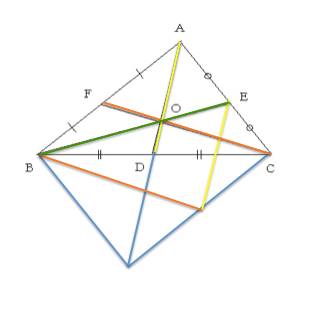
�}�̂悤�ɁA���s�l�ӌ`�ōl�������c
���́�ABC��2�{����A
(1/2)^2+1/2+1/2 �����������̂ŁA
2-(1/4+1)=3/4
�܂��c
3/4�{
^^
NO6�u�O�p��K�v
09/07 17��20���@��M �X�V 09/21
���R�����g�F����̖��ł����C3�ӂ�a,b,c�Ƃ��Cad,be,cf��a,b,c�ŕ\���c�C�Ƃ���Ă������Ƃł���̂ł��傤�ˁB������ƐH�w�������܂����c�B���͍���̌��ʂ����߂Ēm��܂������C�L���Ȏ����Ȃ̂ł��傤���H��
NO7�u��x�Ђ����v 09/13 20��13���@��M
�X�V 09/21
(��)
3�{�̒���AD�CB�CECF��3�ӂƂ���O�p�`�̖ʐς́C
���Ƃ̎O�p�`ABC�̖ʐς� 3/4 �ɂȂ�D
��BC�CCA�CAB �̒��_�����ꂼ��D�CE�CF�Ƃ��C
����AD�Ɛ���BE�̌�_��G�Ƃ��܂��D
G�͐���CF��̓_�ł��D
�܂��CAG�FGD = BG�FGE = CG�FGF = 2�F1 �ł��D
3�{�̒��� AD�CBE�CCF�����O�p�`�� T �Ƃ��C
T �̖ʐς� s(T)�Ƃ����ӂ��ɏ������Ƃɂ��܂��D
�_D��ʂ��ĂȂ�������BE�ɕ��s�Ȓ����Ɛ���CF�Ƃ̌�_�� H �Ƃ��܂��D
��CDH �� ��CBG �ł���C������� CD�FCB = 1�F2�D
DH=(1/2)*BG=(1/2)*(2/3)*BE=(1/3)*BE�D
HG=(1/2)*CG=(1/2)*(2/3)*CF=(1/3)*CF�D
GD=(1/3)*AD�D
T �� ��DHG �͑���(��3�g�̕ӂ̔䂪���ׂē�����)�ł���C
������� 3�F1 �Ȃ̂ŁC
s(��DHG)=(1/3)^2*s(T)=(1/9)*s(T)�D------ (1)
�܂��C
s(��DHG)
=(1/2)*s(��DCG)=(1/2)*(1/3)*s(��DCA)
=(1/2)*(1/3)*(1/2)*s(��ABC)=(1/12)*s(��ABC)�D------ (2)
(1)�C(2)���
(1/9)*s(T) = (1/12)*s(��ABC)�D
�܂�Cs(T)=(3/4)*s(��ABC)�D
�O�p�`�̖ʐςƌ����C���͎��̖�肪��ۂɎc���Ă��܂��D
(���)
��ABC�̊e�ӂ̒�����2�����傫�����̂Ƃ���D
���̎O�p�`�̎����2�_����������2�̐���PQ�������
1������Ƃ��CPQ�̒��_M�̋O�ՂƁC��ABC�̎��Ƃň͂܂�
�镔���̖ʐς����߂�D
���̖��͐ϕ��v�Z�����邱�ƂȂ��ɉ������Ƃ��\�ł��D
�����̗��ꂩ��N����̖��Ƀ`�������W���Ă݂܂��B��
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
