平成19年度　校内研究授業　　　　数学科　

　　　数学�T　　授業指導案

日時	平成１９年１１月１５日(木)			指導者		水の流れ
指導クラス		１年　　　組			場所		教　室
単元名		数学�T　第３章　図形と計量 第３節　§８　球の体積と表面積			使用 教材		改訂版　数研出版「数学�T」 傍用問題集「４ＳＴＥＰ数学�T＋A」
教材観		現在使用している教科書は、生徒のレベルを考えるとやや難しいと感じている。難易度順に、例、例題、応用例題と多く設けられているので、練習問題等精選する必要がある。 また、扱う問題のほとんどが、あらかじめ図形が提示されており、題意の把握には役立つと思っている。
クラス観
指導観
単元の目標		○ 関心・意欲・態度 ・相似形の相似比と面積比・体積比の関係に気づき、図形の計量に活用しようとする。 ・球の表面積や体積がいろいろな方法で求められることに関心をもち、調べようとする。 ○ 数学的な見方や考え方 ・相似形の性質や球の表面積、体積をいろいろな方法で考察することができる。 ○ 表現・処理 ・カヴァリエリの原理を用いて球の体積を導き出すことができる。 ・三角比や正弦定理・余弦定理、三角形の面積の公式、相似形の性質及び球の表面積および体積の公式などを用いて平面図形や空間図形を計量することができる。 ○ 知識・理解 ・相似形の面積比・体積比について理解し、基礎的な知識を身につけている。 ・球の表面積や体積の公式について理解し、基礎的な知識を身につけている。
本時の目標		カヴァリエリの原理に基づいて球の体積の求め方や、球の表面積の求め方を理解し、公式を利用して体積や表面積などを計量することができる。						本時の位置		第３節 10時間中 ７時間目
評価規準		・ カヴァリエリの原理に基づいた体積の考え方を身につけ、具体的な図形の体積を考察することができる。【数学的な見方や考え方】 ・ 球の体積や表面積の公式を利用して、平面図形や空間図形を計量することができる。 【表現・処理】
本時の展開
時間	学習項目		指導内容・学習活動						指導上の留意点・観点別評価
２分	１本時の目標の把握		・事前に本時の授業の流れをプリントにしてあるから、目標の確認。						・配布プリントの予習を確認しながら机間指導をする。
８分	２三角形の面積 ３カヴァリエリの原理の紹介 ４パズルの問題 ５円の面積 ６角錐・円錐の体積		問題１：三角形の面積公式の確認。 カヴァリエリの原理 ２つの図形を１つの線に平行な線で切ったとき、切り口の長さが等しいならば、２つの図形の面積は等しい。 注：カヴァリエリの原理が成り立っていることを確認 問題２：ある図形を移動したとき、移動面積を求める。 問題３：円の面積公式πｒ^２の確認。 注：円の直径と円周の比率は一定だから、その比を円周率πとする。 発問：円をどのようにして細かく切ると良いかを聞く。 �@　円の中心にして、扇形に切る方法 �A 円の中心にして糸で蒔きつける。 問題４：三角錐・円錐の体積公式(1/3)Sｈの確認。 （ただし、Sは底面積、ｈは高さ） 注：２つの模型を準備して説明する。 注：角錐・円錐の体積は角柱･円柱の体積の３分の１であることを確認。 ＜インターネットをつないで、動画を見せる。２分＞						・ 机間指導したとき、考え方の分からない生徒にヒントを与える。 ・カヴァリエリの原理を用いて求めることができるか考えさせる。【見】 ・小学校で円の面積を求めているから、生徒に確認【表】【知】 ・小学校で三角錐の体積を求めているから、生徒に確認【表】【見】
１５ 分	７球の体積		問題５：アルキメデスは球の体積を知っていたか。 注：アルキメデスの墓標に描かれた円柱・円錐・球の図柄を紹介する。 発問：ここにある模型を使い球の体積を求める方法を考えてみなさい。 �@ 円柱と球に水を入れて実験する （動画を見せる：3分） �A　円錐と球に粉ぬかを入れて測る。（紹介だけ） �B 内接する円柱と外接する円柱に分割する。 （持参したゆで卵をスライスする） 問題６：カヴァリエリの原理を利用して円柱、円錐、半球を用いて、球の体積を求める。 カヴァリエリの原理 ２つの立体を１つの平面に平行な平面で切ったとき、切り口の面積が常に等しいならば、２つの立体の体積が等しい 注：「円柱の体積」＝「円錐の体積」＋「半球の体積」 したがって、球の体積を求めさせる。 公式の確認　(4/3)πｒ^3「身の上、心配ある、参上」						・ 生徒にどうようにしたら球の体積が求まるかを聞く。【表】【知】 ・生徒の姿を観察する。【関】 ・カヴァリエリの原理を確認し、計算は要点のみ解説。 ・三平方の定理を用いる ・断面積に着目 【見】
１０ 分	８球の表面積		問題７： 球の表面積を求める方法を考える。 発問：生徒にどのような方法があるかを聞く。 �@　球の表面積を糸で覆い尽くして測る。 　　（動画を見せる：3分） �A 球の中心を頂点とする角錐状の立体に分割する。 �B 球をタマネギの皮のように剥がしていき、円錐状に分割する。＜タマネギを持参＞ �C 球を円錐台の立体に分割する。 （再度　スライスしたゆで卵をみせる） 公式の確認　４πｒ^２「心配ある事情」						・生徒にどうようにしたら球の表面積が求まるかを聞く。【表】【知】 ・生徒の姿を観察する。【関】
１０分	９公式の利用		問題８　教科書：１４５ページ練習４０ （アルキメデスの墓標に描かれた図柄） 注：球の表面積と円柱の測面積の比較 注：円 注：円柱と球の体積比、円柱と球の表面積の比の関係を知る。 ＜時間があれば、アルキメデスに関する資料を紹介＞ ＜時間があれば、ｎ次元の球の体積公式の紹介＞						・机間指導したとき、解けていない生徒にヒントを与える。 【評価】【表】 ・比の関係が一致していることに関心を向けさせる。【関心】
５分	10本時の内容の確認。		・ 球の体積と表面積の公式を振り返る。 ・ 次回の予告						・生徒に感想を聞く。

数学�T　第３節　図形と計量　§８　球の体積と表面積　＜予習プリント＞

　　以下の問題について答えなさい。

問題１：底辺がa、高さがｈの三角形の面積を求めよ。

　　　

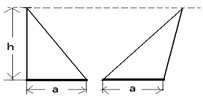
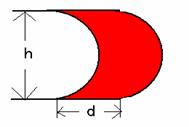
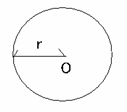
問題２：次の図形を移動したとき、移動面積を求めよ。　　問題３：半径ｒの円の面積を求めよ。

　　　　　　　　　　　　　　　

　　

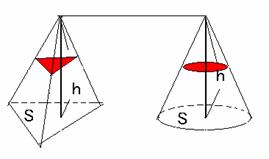
　問題４：底面積S、高さｈの三角錐・円錐の体積を求めよ。

　　　　　　

問題５：アルキメデスは球の体積を知っていたかを、調べてきなさい。

　　　　皆さんは、どんな方法で球に体積を求めようとしますか。実験を含めて幾つか考えてきなさい。

次に、半径ｒの球の体積を書きなさい。

問題６：カヴァリエリの原理を利用して円柱、円錐、半球を用いて、球の体積を求める方法を

　　　教科書から、調べてきなさい。

　　　

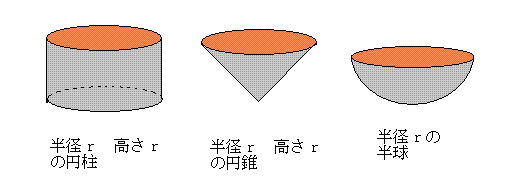
問題７：球の表面積を求める方法を幾つか考えてきなさい。

問題８：教科書：１４５ページの練習４０を解いてきなさい。

（アルキメデスの墓標に描かれた図柄）

指針１：授業の受け方

　授業は次の目標にしたがって実施します。授業で身に付ける事項を理解してください。

�@　数学における基本的な概念や原理・法則の理解を深め、

�A　事象を数学的に考察し処理する能力を高め、

�B　数学的活動を通して創造性の基礎を培うとともに、

�C　数学的な見方や考え方のよさを認識し、

�D それらを積極的に活用する態度を育てる。

(1) 新しく学習する内容を理解するだけでなく、学習する価値や学習の必要性も学びましょう。

(2)「なぜ」「どうして」という疑問を持ちながら授業に参加しましょう。

(3) 授業では新しい内容を理解する以上に考え方や処理の仕方を学びましょう。

また、自分の考え方を大切にすると同時に友だちのよい考え方も参考にしましょう。

(4) 予習では「疑問」を、復習では「納得」を観点に頑張りましょう。

(5) 授業で解決する課題については、いろいろな方法で解決するようにしましょう。

指針２：学力向上のための方策

(1) 練習問題をたくさん解くことより、１つの問題を大切にし、いろいろな角度から考える学習習慣を
身に付けましょう。例えば、この問題の解き方は前に解いたのと似ているとか、この練習問題の
条件を変えたらどんな新しい問題ができるかなどを考えたり、問題の仕組みも考えましょう。

(2)考えることの楽しみや自分で問題を解決したときの満足感をより多く経験しましょう。

(3)数学はじっくり考える教科です。特に、今まで学習した内容に結びつける努力をし、覚える内容は
できるだけ少なくしましょう。