toukou20

　　　　　　　　　 平成１５年７月２７日

第２回　「手紙を３つに折る方法を発見しよう」
５月２６日　６月２日　６月９日　６月１６日　実施

最近手紙を書くことは少なくなって来ているが、便せんを使って手紙を書いたあと、その手紙を２回折って封筒に入れて出すのが普通である。しかし、封筒に入れることができない。やむを得ず便せんを３等分すると封筒の幅に綺麗に納まる。おそらく定型の封筒に決められているのだろう。おおよその目分量で３等分するのは難しい。そこで、「便せんを３等分する方法」を考えてください。

１．便せんの縦横の比率を計ってください。

生徒の活動：Ａ４のわら半紙を渡して、縦と横の長さを測らせる。
結果は縦２９．７ｃｍ　、横　２１．０ｃｍで比率（縦÷横）は１．４１４

２．この用紙を半分に折った形と元の用紙との関係を考えてください。

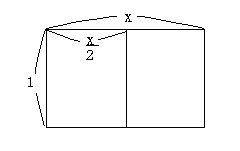
　　ｘ＝√２ですからと言う相似の関係を保っています。

３．他にこの縦横の比率をもった用紙を考えてください。また、この比率を一般に何と呼ばれていますか。
　

生徒の活動：ノート類、教科書、郵便はがき、テレホンカード等身近にあるものを測る　

解説：この中には、既に知っている比の値√２がある。ちなみに、√２をシルバーセクションという。

さらに、（１＋√５）／２＝１．６１８となる比もある。この値がゴールデンセクションです。

　　　　　　　　　　　　　　　（パルテノン　神殿）

　　　　　　　　　　（http://plus.maths.org/issue3/fibonacci/　から引用）

４．チャレンジ１：正三角形を作る方法

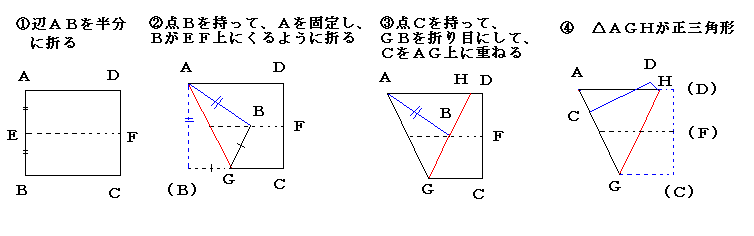
　チャレンジ２：辺を３等分する方法
（１）相似比を利用したとき　

方法１
　

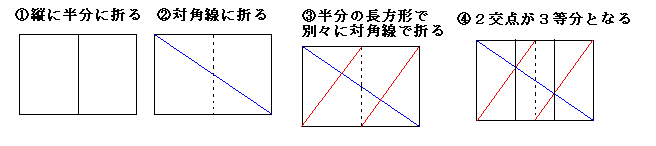
方法２

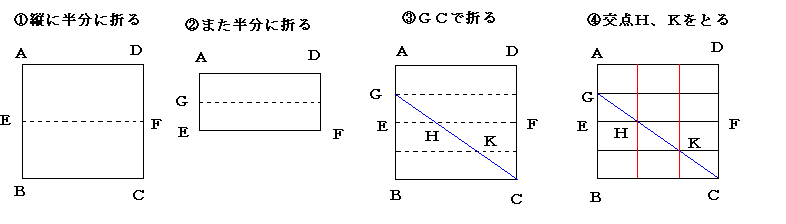
（２）縦・横の比が１：√２を利用したとき
方法３

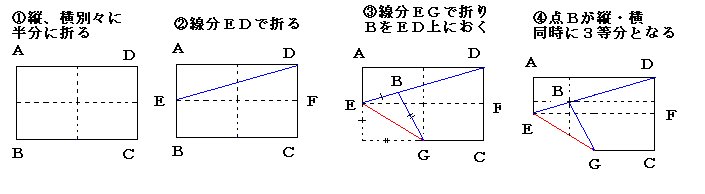
チャレンジ３：辺を５等分する方法

（これは夏休みの課題にしてある）

５．生徒の感想

（１）３等分に折る方法は、いろいろあると思った。証明するのは難しいけど、分かると楽しいと思った。

（２）相似比を使うと簡単に紙を３等分できることが分かった。この他にもあるから家で確かめて、使えるようにしたい。

（３）手紙などを３等分する方法を学ぶことができた。最初、何でこんなことをするのかぁと思ったが、役に立ちそうなので日常生活に生かしたいです。

（４）手紙でこんなことしたら折り目がついて、かえって読みにくくなると思います。

（５）手紙を縦・横に半分に折った形なら定型の封筒に入るから、無理しなくて良いのに。

（６）方法３では、縦・横が同時に３等分した点になっていることに気がついた。

６．追伸：「折る紙の数学」講談社ブルーバックス講談社の著者渡辺勝　氏から次のようなメールを頂きました
（１）２００１年８月のメール

「数学の重要性」

　数学を学ぶと言う事は、もはや公理、定理や公式を使って証明する事、　計算する事では無くなっていると思う。
　　数学を学ぶと言う事は、新しい定理や公式を発見する事であり、問題を解決する能力を開発する事、活性化する事であると言って良いのでは
　ないか。それゆえに、政治や経済の分野においてもその数学が重要となるのです。

「創造力」と言う言葉はごく一般的ですが、「工夫力」とはあまり言わないようです。　
「創造力」とは、ひらめき力の事であり、「工夫力」とは、そのひらめいた物、ひらめいた事を具体化、具現化するプロセスにおける問題解決力と言って良い。
　　企業社会における、創造力と工夫力とは、すなわち「ヨシ！　１００円で作ろう」と言う創造力と「どのようにしてそれを作るのか」と言う工夫力の関係である。
　　
　　其処でこの「工夫力」を開発すると言う事、それは例えば、一枚の長方形の用紙を生徒に与え、「その用紙の面積を三等分せよ」とする時、どのようにこの問題を解決するのかと言う能力を開発するに等しく、これは大変重要な事である。解答は一通りではありません。

学生たち、いや、多くの社会人が数学嫌いである現状は多いに憂慮されなければならない。私は「工夫力の開発、活性化のために、提案を続けていきたいと思います。

　問題
　「用紙 B５版の面積の１/３となる正方形を作りなさい」この用紙を使います。
（２）２００１年９月のメール

「工夫力」

生徒に一枚、ペーパーを与えてください。多くの場合、それが、Ｂ５版あるいはA4版コピー用紙などであるとしましょう。
　　それでは、この用紙を使って正方形を作って下さい。　出来ましたか？ここまでは小学生でも出来ると思います。
　（長いほうの辺に短いほうの辺の長さを取り、その点で折ればよい）　　　　
　　次に、この正方形の面積を１として、その面積の１/2となる正方形をつくってください。　　　　
どうしますか？
　四隅を中心点に合わせる様に折る。（小学生でも出来るかもしれません）
　　それでは、その一辺となった長さを考えて見ましょう、√２/２（２分の　√２）となっていることが判ります。
そうです面積が1/2となっているわけですから、その一辺の長さは√１/2=√２/２となるわけですね。
　では面積を1/2にする方法はこれだけなのでしょうか？
　多くの方法がありますので工夫してください、どの様に見つけるのか、
　プロセスによっては、中学生、高校生向けのテーマとなります。
　では、１/3となる正方形はどうでしょう、少し難しくなってきます。１/4は？これは簡単に出来そうですね、ある方法は小学生でも出来るかも知れません、
然し他の方法はどうでしょうか？
　順次、１/5 1/6・・と進めてください。
　　

更に高度なテーマとしてこのＢ5版紙の面積の１/３となる正方形をつくってください。
　　一枚のペーパーを手に実感しながら「工夫する力」を高める事になります。
　次に、それらの辺を、図形として、あるいは計算値として求め確認します。